Aufgabe 3
Der in Abbildung 1 dargestellte Körper  mit den Eckpunkten
mit den Eckpunkten  und
und  hat folgende Eigenschaften:
hat folgende Eigenschaften:
 ist ein Rechteck in der
ist ein Rechteck in der  -Ebene,
-Ebene,  ist ein Rechteck in einer zur
ist ein Rechteck in einer zur  -Ebene parallelen Ebene. Die Vierecke
-Ebene parallelen Ebene. Die Vierecke  und
und  liegen in Ebenen, die parallel zur
liegen in Ebenen, die parallel zur  -Ebene verlaufen.
-Ebene verlaufen.
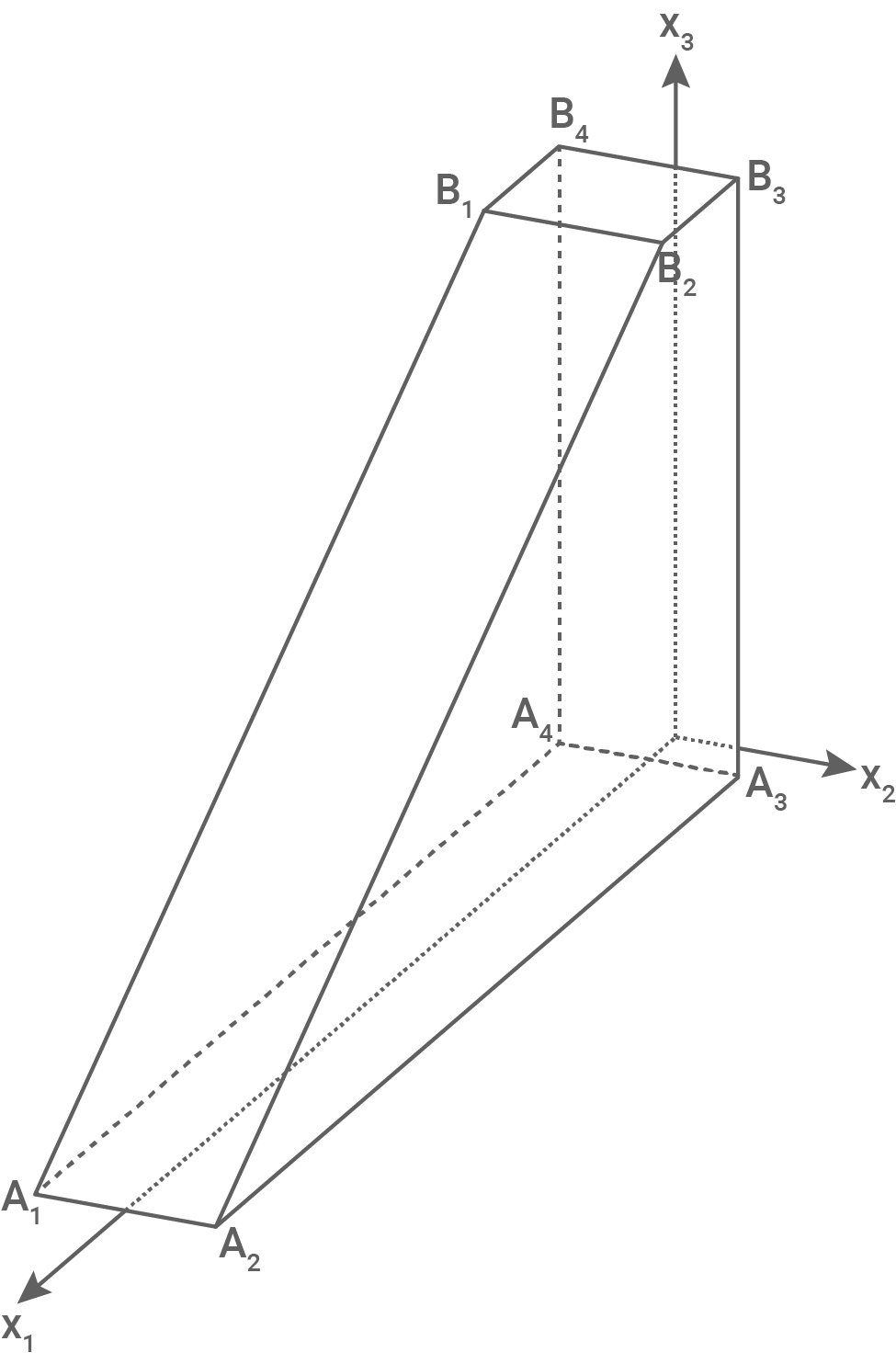 Der Körper
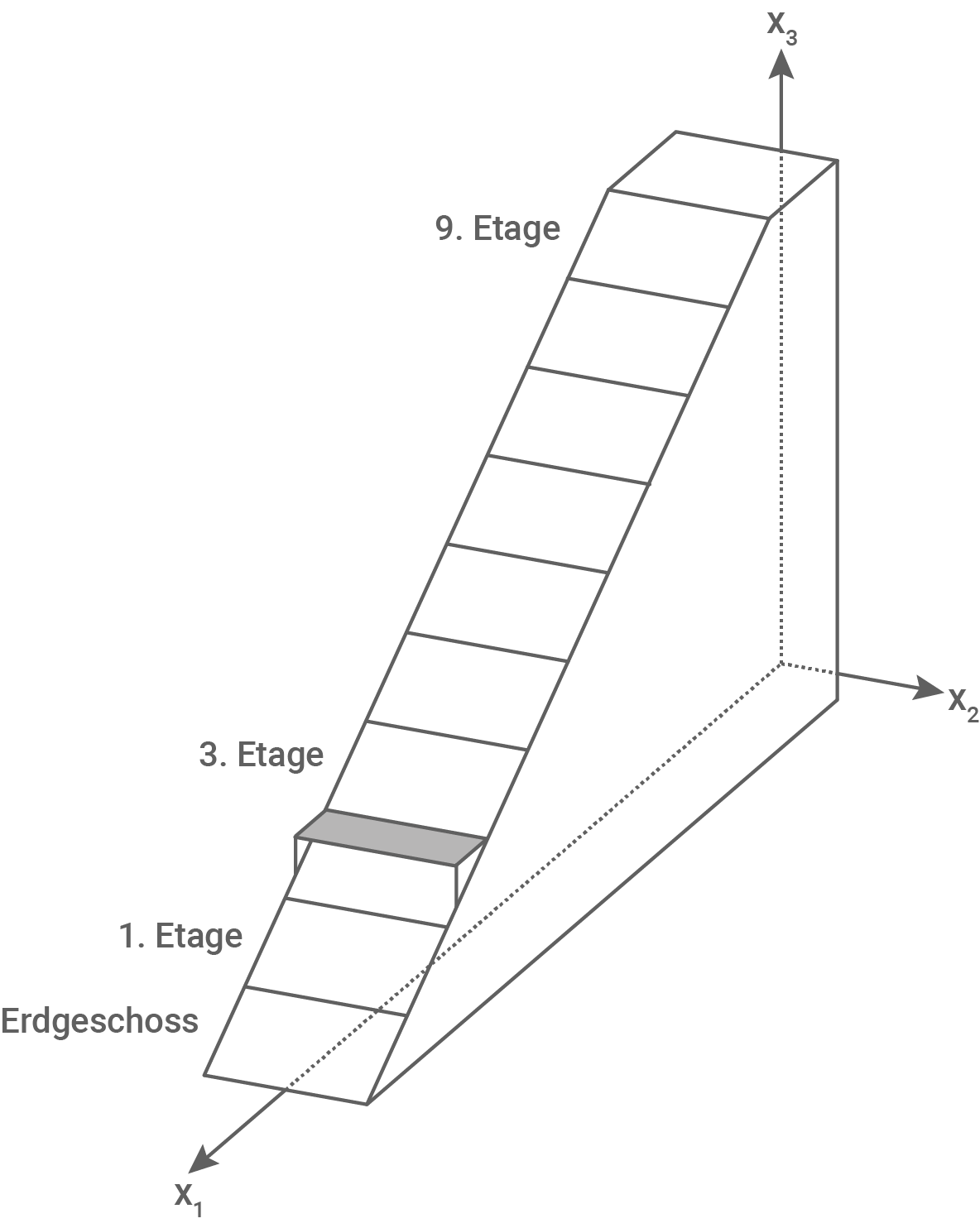
Der Körper  ist Teil eines mathematischen Modells eines Architekturbüros zur Planung eines neuen Hotels. Das Hotel soll zehn Stockwerke gleicher Höhe besitzen. Für die an die Schrägen angrenzenden Hotelzimmer sind von der 1. bis zur 9. Etage Balkone geplant. Als Beispiel ist in Abbildung 2 der Boden des Balkons für die 3. Etage dargestellt.
Eine Längeneinheit im Modell entspricht einem Meter in der Realität.
ist Teil eines mathematischen Modells eines Architekturbüros zur Planung eines neuen Hotels. Das Hotel soll zehn Stockwerke gleicher Höhe besitzen. Für die an die Schrägen angrenzenden Hotelzimmer sind von der 1. bis zur 9. Etage Balkone geplant. Als Beispiel ist in Abbildung 2 der Boden des Balkons für die 3. Etage dargestellt.
Eine Längeneinheit im Modell entspricht einem Meter in der Realität.
 ist eine Ebene der Schar modelliert. Der Boden des Balkons für die 3. Etage liegt z. B. in der Ebene
ist eine Ebene der Schar modelliert. Der Boden des Balkons für die 3. Etage liegt z. B. in der Ebene  Das Hotel soll aus drei Gebäuden bestehen, die jeweils die gleiche Form besitzen. Durch den Körper
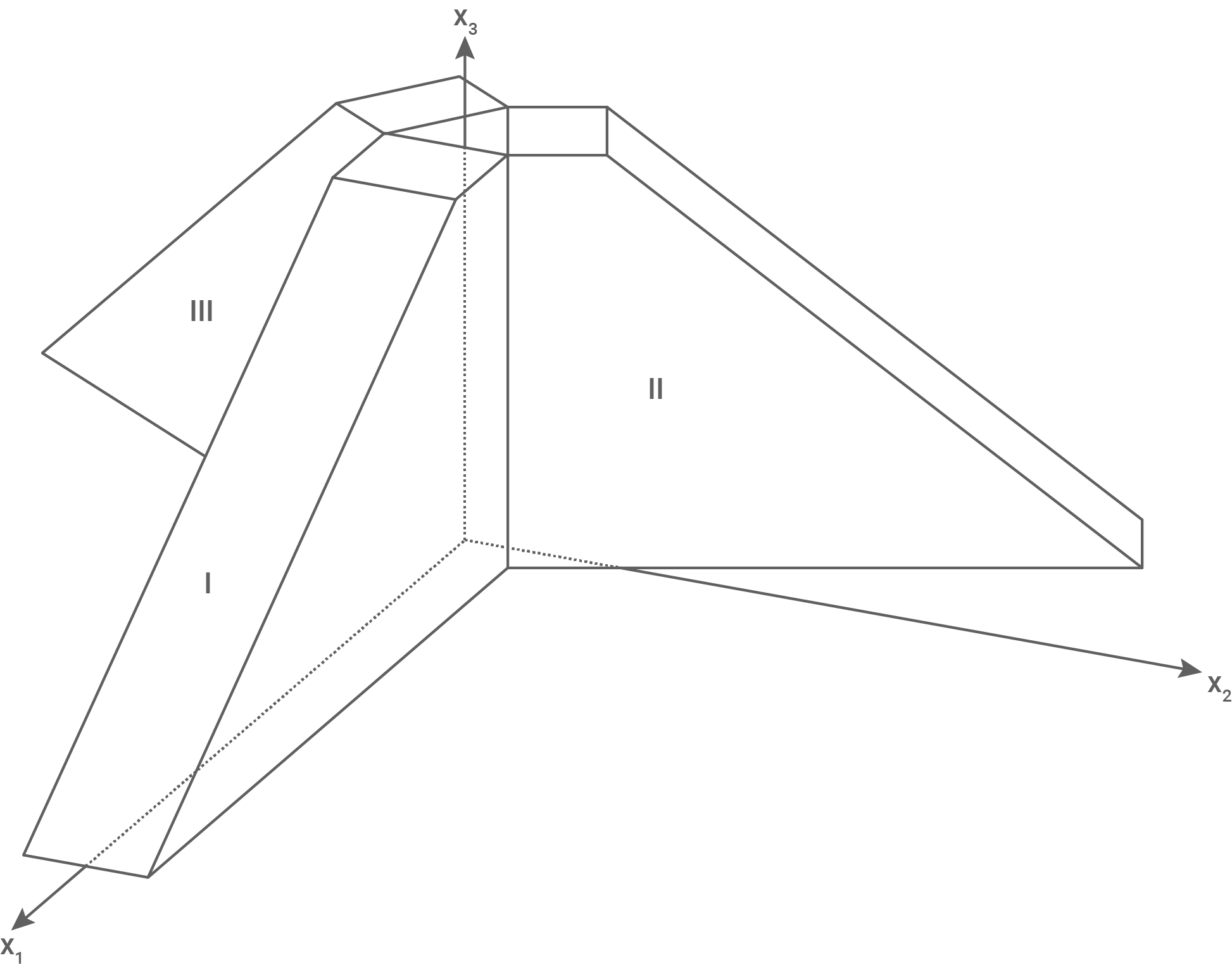
Das Hotel soll aus drei Gebäuden bestehen, die jeweils die gleiche Form besitzen. Durch den Körper  wird Gebäude I modelliert, die Gebäude II und III sind gegenüber Gebäude I jeweils um
wird Gebäude I modelliert, die Gebäude II und III sind gegenüber Gebäude I jeweils um  gedreht (siehe Abbildung 4). Alle drei Gebäude stehen so aneinander, dass sie einen dreieckigen Innenhof bilden. In der Modellierung liegt dieser Innenhof in der
gedreht (siehe Abbildung 4). Alle drei Gebäude stehen so aneinander, dass sie einen dreieckigen Innenhof bilden. In der Modellierung liegt dieser Innenhof in der  -Ebene.
-Ebene.
Sechs der Eckpunkte sind gegeben durch







Abbildung 1
a)
(1)
Gib die Koordinaten des Punktes  an.
an.
(2)
Begründe, dass die Seitenfläche  ein Trapez ist, und berechne das Volumen des Körpers
ein Trapez ist, und berechne das Volumen des Körpers 
(1 + 3 Punkte)

Abbildung 2
b)
Durch 

(1)
Zeige: Für jeden Wert von  mit
mit  liegt der Punkt
liegt der Punkt  auf der Strecke
auf der Strecke 
(2)
Die Menge aller Punkte der Bodenfläche des Balkons für die 3. Etage wird durch die Parametergleichung


 beschrieben.
beschrieben.
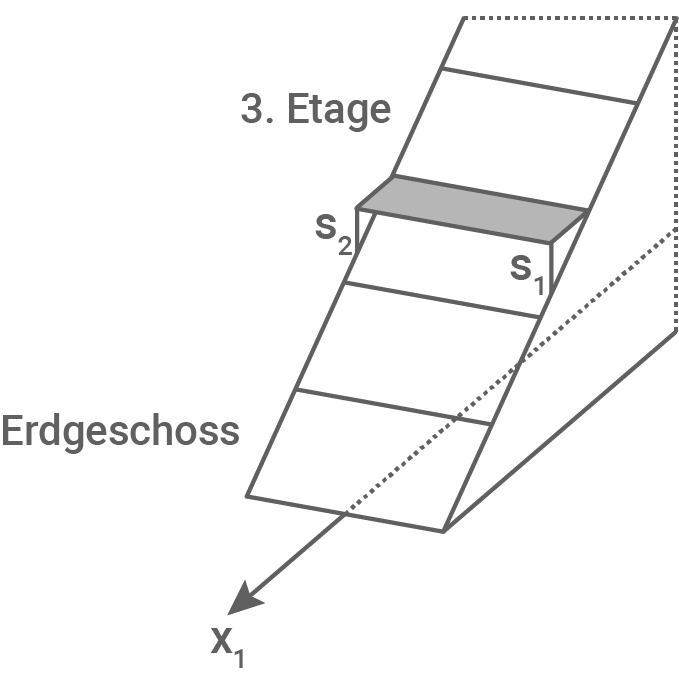
Der Balkon ist wie in Abbildung 3 dargestellt auf zwei vertikalen Stützen  und
und  gelagert. Berechne die Länge der Stütze
gelagert. Berechne die Länge der Stütze 

Abbildung 3
(4 + 4 Punkte)

Abbildung 4
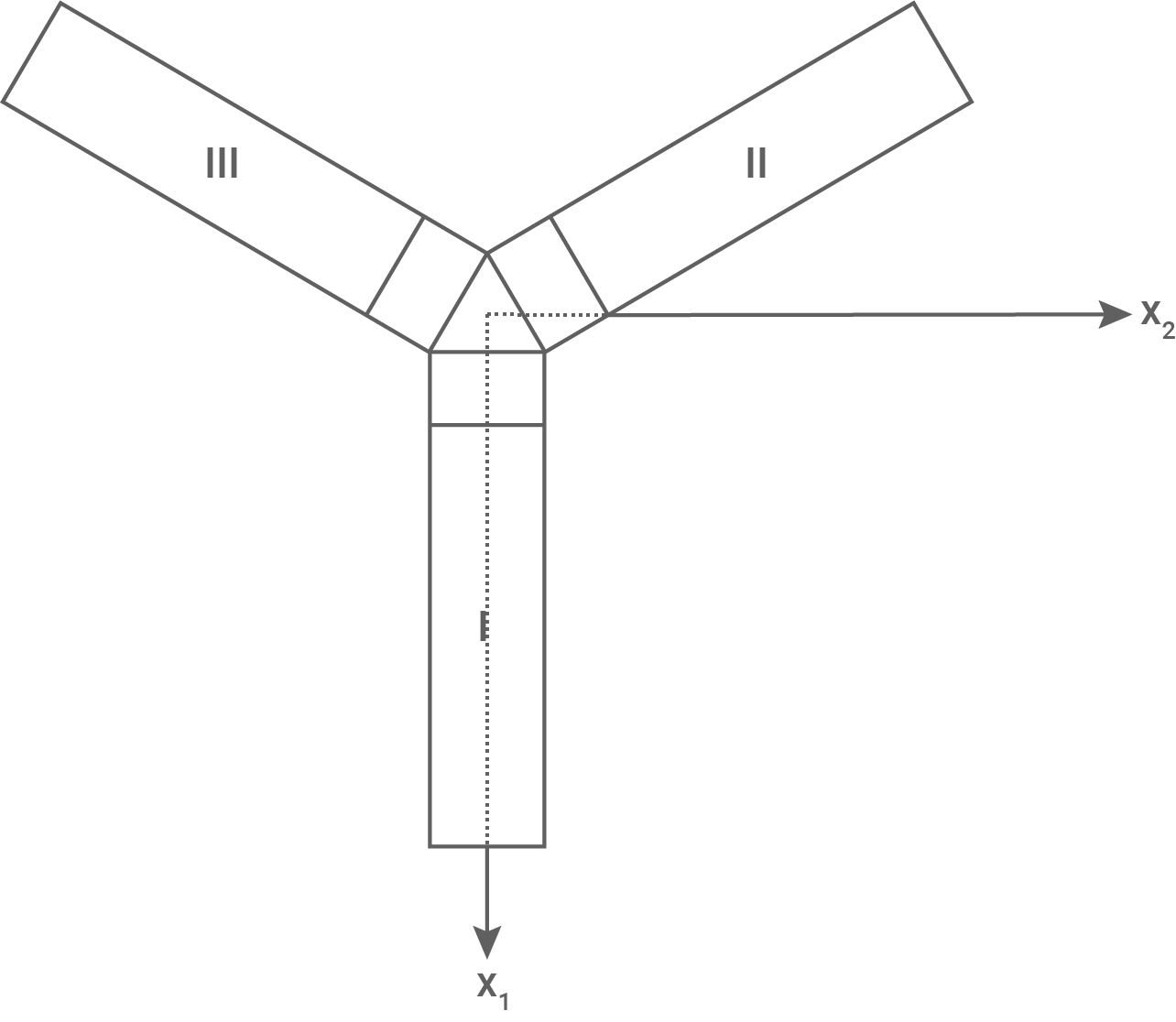
Abbildung 5 zeigt das Modell des Hotels von oben.

Abbildung 5
c)
Der Innenhof  hat die Form eines gleichseitigen Dreiecks.
hat die Form eines gleichseitigen Dreiecks.
(1)
Ermittle rechnerisch die Koordinaten des Punktes 
 Zur Kontrolle:
Zur Kontrolle: ![\(P\left(-\frac{2 \cdot \sqrt{75}}{3} \mid 0 \mid 0\right) \approx P(-5,77\mid 0 \mid 0).\bigg]\)](https://mathjax.schullv.de/1b318251557a8a0f53f186c8a05caf5e5ca487f2ae98213cb279a6adebf24c6d?color=5a5a5a)
(2)
Berechne den Abstand von  zum Koordinatenursprung
zum Koordinatenursprung 
(3 + 2 Punkte)
d)
(1)
Stelle eine Koordinatengleichung der Ebene  auf, in der die Fläche
auf, in der die Fläche  liegt.
[Zur Kontrolle:
liegt.
[Zur Kontrolle: ![\(\left.F: 3 \cdot x_1+4 \cdot x_3=150.\right]\)](https://mathjax.schullv.de/a22594dacc4a8d73df4da4101a93b0531016b31300a82533bfb94ce7aee7bd39?color=5a5a5a)
(2)
In der Mitte des Innenhofs steht ein Mast, dessen Spitze im Punkt  liegt. Zu einem bestimmten Zeitpunkt steht die Sonne so, dass die Sonnenstrahlen die Richtung
liegt. Zu einem bestimmten Zeitpunkt steht die Sonne so, dass die Sonnenstrahlen die Richtung  besitzen.
Untersuche, ob der Schatten der Spitze des Masts zu diesem Zeitpunkt innerhalb der Fläche
besitzen.
Untersuche, ob der Schatten der Spitze des Masts zu diesem Zeitpunkt innerhalb der Fläche  liegt.
liegt.
(4 + 4 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
(2)
Trapezform begründen
Anhand der  - und
- und  -Koordinaten der Punkte der Seitenfläche
-Koordinaten der Punkte der Seitenfläche  wird auf
wird auf  geschlossen.
Somit handelt es sich um ein Trapez.
Seitenlängen und Volumen berechnen
geschlossen.
Somit handelt es sich um ein Trapez.
Seitenlängen und Volumen berechnen




![\( \approx 47,11 \;\text{[LE]}\)](https://mathjax.schullv.de/9564117d430ebca211c2e87f67f609e2992d6d5d20210e08ef457158f4101812?color=5a5a5a)




![\( \approx 7,11\;\text{[LE]}\)](https://mathjax.schullv.de/214189ea25312669b382819664abe62bda1a88c3bae03bb5e5b4c01d7a0afcd0?color=5a5a5a)


![\(=\left|\pmatrix{\frac{\sqrt{75}}{3}\\5\\30}-\pmatrix{\frac{\sqrt{75}}{3}\\5\\0}\right|= 30\;\text{[LE]}\)](https://mathjax.schullv.de/9f564575986864582e25a8396f9aaf8b78208f6f6939708d67ea63318ac4aede?color=5a5a5a)


![\(=\left|\pmatrix{50\\5\\0 }-\pmatrix{50\\-5\\0}\right|=10\;\text{[LE]}\)](https://mathjax.schullv.de/56549e1af8ec50ada39943b0e2245889408eb0b5db172f5aff15685fcfe6dc41?color=5a5a5a) Es gilt:
Es gilt:
![\(\begin{array}[t]{rll}
V_{\text {Körper }}&=& A_{\text {Trapez }} \cdot h \\[5pt]
&=& \frac{\left(\left|\overline{A_2 A_3}\right|+\left|\overline{B_2 B_3}\right|\right) \cdot\left|\overline{A_3 B_3}\right|}{2} \cdot\left|\overline{A_1 A_2}\right| \\[5pt]
&\approx& 8134 \;\text{[VE]}
\end{array}\)](https://mathjax.schullv.de/d2dd3b33db9aee3af9f5584c3ea029e5176cd07ff830cfd30a5016d9bf041379?color=5a5a5a)
b)
(1)
Eine Parametergleichung der Strecke  ist gegeben durch:
ist gegeben durch:
![\(\begin{array}[t]{rll}
h: \vec{x}&=&\overrightarrow{O A_2}+t \cdot \overrightarrow{A_2 B_2} \\[5 pt]
&=& \pmatrix{50\\5\\0} + t \cdot \pmatrix{-40\\0\\30}
\end{array}\)](https://mathjax.schullv.de/e5db4d8ea0140c5a75ceef9ae6357aeac2f18fcf6c33ceee5651fabed0cab6c2?color=5a5a5a) mit
mit  Koordinaten des Punktes gleichsetzen:
Koordinaten des Punktes gleichsetzen:

 Dies führt zu folgendem LGS:
Dies führt zu folgendem LGS:
 Aus der dritten Zeile folgt:
Aus der dritten Zeile folgt:
![\(\begin{array}[t]{rll}
30\cdot t&=& 0,75\cdot a&\quad \scriptsize \mid\;:30 \\[5pt]
t&=&0,025\cdot a
\end{array}\)](https://mathjax.schullv.de/9ecc6175693fbc19a36abc7c6a0f9df600ca4e3757f93b580eca73e220876847?color=5a5a5a) Einsetzen in die erste Zeile ergibt eine wahre Aussage:
Einsetzen in die erste Zeile ergibt eine wahre Aussage:
![\(\begin{array}[t]{rll}
50 -40\cdot (0,025\cdot a)&=& 50-a \\[5pt]
50-a &=& 50-a
\end{array}\)](https://mathjax.schullv.de/cbf5bb711053c23405bc48949d5e5a501e25f4e09a88efe330eb77a3b53c1740?color=5a5a5a) Wegen
Wegen  gilt
gilt  Damit liegt für jedes
Damit liegt für jedes  mit
mit  der Punkt
der Punkt  auf der Strecke
auf der Strecke 
(2)
1. Schritt: Geradengleichung aufstellen, auf der  liegt
Mit
liegt
Mit  und
und  ergeben sich die Koordinaten des Eckpunktes des Balkons.
ergeben sich die Koordinaten des Eckpunktes des Balkons.


 entspricht dem oberen Ende der Stütze
entspricht dem oberen Ende der Stütze  Die Stütze
Die Stütze  wird als Strecke modelliert. Diese Strecke ist in folgender Geraden enthalten:
wird als Strecke modelliert. Diese Strecke ist in folgender Geraden enthalten:
 mit
mit  2. Schritt: Koordinaten des Schnittpunktes von
2. Schritt: Koordinaten des Schnittpunktes von  mit der Strecke
mit der Strecke  bestimmen
Geraden
bestimmen
Geraden  und
und  gleichsetzen:
gleichsetzen:
 Daraus ergibt sich folgendes LGS:
Daraus ergibt sich folgendes LGS:
 Mit dem solve-Befehl des GTRs ergibt sich aus der ersten Zeile
Mit dem solve-Befehl des GTRs ergibt sich aus der ersten Zeile  Einsetzen in die dritte Zeile:
Einsetzen in die dritte Zeile:
![\(\begin{array}[t]{rll}
9+u&=& 30 \cdot 0,225&\quad \scriptsize \mid\;-9 \\[5pt]
u&=& -2,25
\end{array}\)](https://mathjax.schullv.de/b2f4acc316c9deb735ac107eb522a1befcbc6bd8b7753eb4aa288e3aaa3fee96?color=5a5a5a) Die Stütze
Die Stütze  besitzt eine Länge von
besitzt eine Länge von 
c)
(1)
Aus Symmetriegründen muss der Punkt  auf der
auf der  -Achse liegen.
Die Seiten des Dreiecks
-Achse liegen.
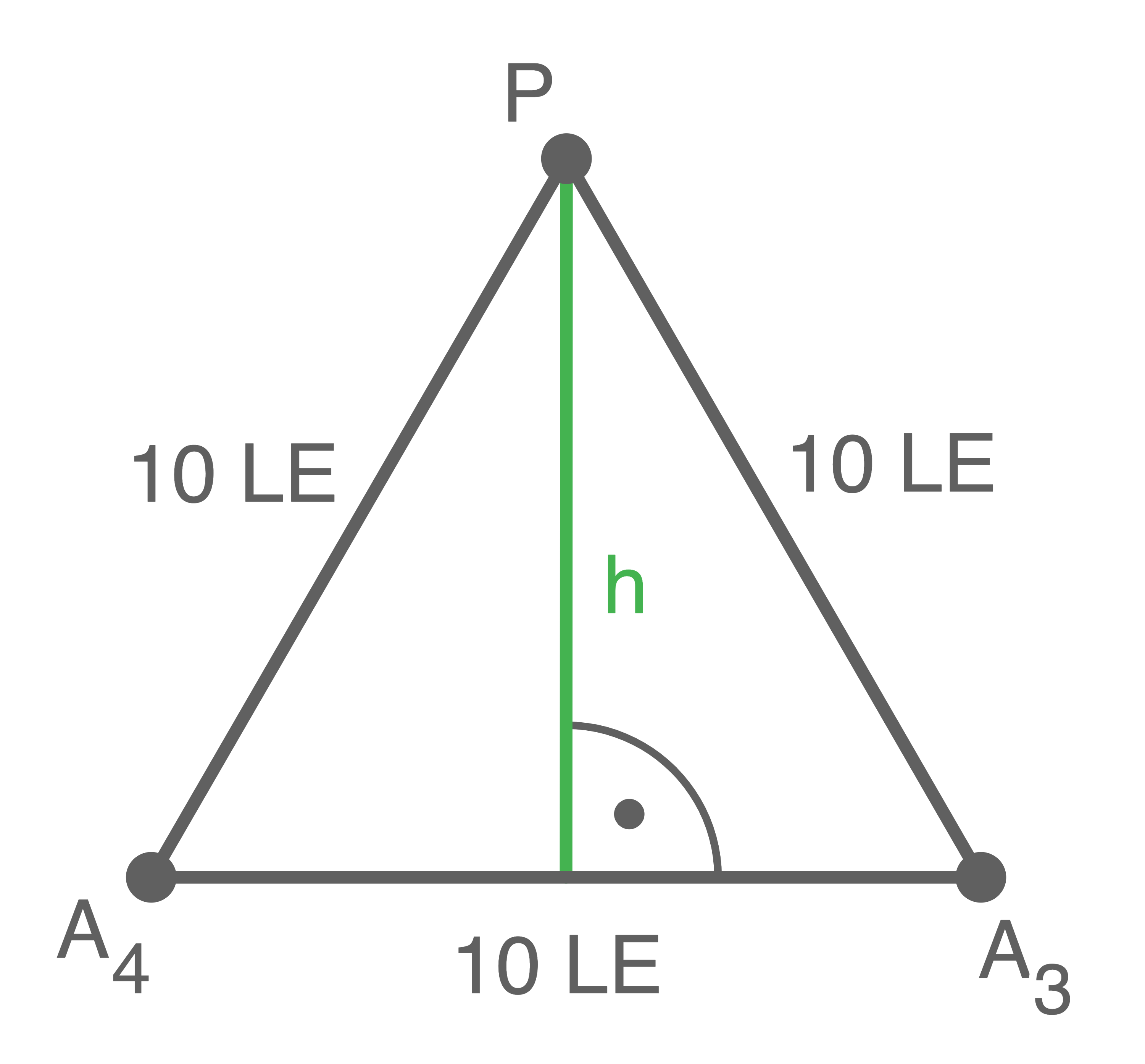
Die Seiten des Dreiecks  besitzen eine Länge von
besitzen eine Länge von ![\(\left|\overline{A_3 A_4}\right|=10\;\text{[ LE ]}.\)](https://mathjax.schullv.de/8d6971a0f293b22a6de69c830ccc9cf3e7ee3e6024dd09fd8fd65e25b8f353ce?color=5a5a5a)
Der Mittelpunkt der Strecke  hat die
hat die  -Koordinate
-Koordinate  Für die
Für die  -Koordinate
-Koordinate  von
von  gilt somit:
gilt somit:
 Die gesuchten Koodinaten ergeben sich zu:
Die gesuchten Koodinaten ergeben sich zu:

Satz des Pythagoras:
![\(\begin{array}[t]{rll}
\left(\dfrac{10}{2}\right)^2+h^2&=&10^2 &\quad \scriptsize \mid\;-5^2 \\[5pt]
h^2&=& 75 &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
h&=& \sqrt{75} \\[5pt]
&=&5 \cdot \sqrt{3}\;\text{[LE]}
\end{array}\)](https://mathjax.schullv.de/3a739f7d844d3221efa8ffc37ef6f3bbd4136cf55a8b6443fbddf0eed2e6fd55?color=5a5a5a)

Hilfsskizze zum besseren Verständnis
(2)
d)
(1)
1. Schritt: Einen Normalenvektor von  bestimmen
bestimmen





 Die Orthogonalitätsbedingungen
Die Orthogonalitätsbedingungen  und
und  führen auf folgendes LGS:
führen auf folgendes LGS:
 Aus der ersten Zeile folgt
Aus der ersten Zeile folgt  Einsetzen in die zweite Zeile ergibt:
Einsetzen in die zweite Zeile ergibt:
![\(\begin{array}[t]{rll}
-40 \cdot n_1 +30 \cdot n_3&=&0 \\[5pt]
-40 \cdot n_1 &=& -30 \cdot n_3 &\quad \scriptsize \mid\;:(-40) \\[5pt]
n_1&=&\dfrac{3}{4} \cdot n_3
\end{array}\)](https://mathjax.schullv.de/6903bb0d0ebbd9e4eb6740b8e0ee87bbf939ec7260c322a428d88e5b5e5d9ea0?color=5a5a5a) Die Wahl von
Die Wahl von  liefert als einen möglichen Normalenvektor von
liefert als einen möglichen Normalenvektor von  2. Schritt: Koordinatengleichung aufstellen
2. Schritt: Koordinatengleichung aufstellen
 Koordinaten von
Koordinaten von  einsetzen:
einsetzen:
![\(\begin{array}[t]{rll}
3\cdot 50 +4\cdot 0&=& c\\[5pt]
150&=&c
\end{array}\)](https://mathjax.schullv.de/fe5a0d6fa97da0142cccfabdabd026c9f74c69d186ba9c02790c02320380de78?color=5a5a5a) Somit ergibt sich die Ebenengleichung
Somit ergibt sich die Ebenengleichung 
(2)
Geradengleichung durch Punkt  mit Richtungsvektor
mit Richtungsvektor  aufstellen:
aufstellen:
 mit
mit  Es werden die Koordinaten des Schnittpunkts
Es werden die Koordinaten des Schnittpunkts  von
von  und
und  berechnet:
Aus der Geradengleichung folgen die Koordinaten
berechnet:
Aus der Geradengleichung folgen die Koordinaten 
 und
und  Einsetzen in die Ebenengleichung
Einsetzen in die Ebenengleichung 
 Auflösen mit dem GTR nach
Auflösen mit dem GTR nach  ergibt
ergibt  Einsetzen in die Geradengleichung
Einsetzen in die Geradengleichung  ergibt die Koordinaten von
ergibt die Koordinaten von 


 Die
Die  -Koordinate von
-Koordinate von  ist größer als
ist größer als  Der Schatten der Spitze des Masts liegt also nicht innerhalb der Fläche
Der Schatten der Spitze des Masts liegt also nicht innerhalb der Fläche 