Aufgabe 1
Gegeben ist die Funktion  mit der Gleichung
mit der Gleichung 
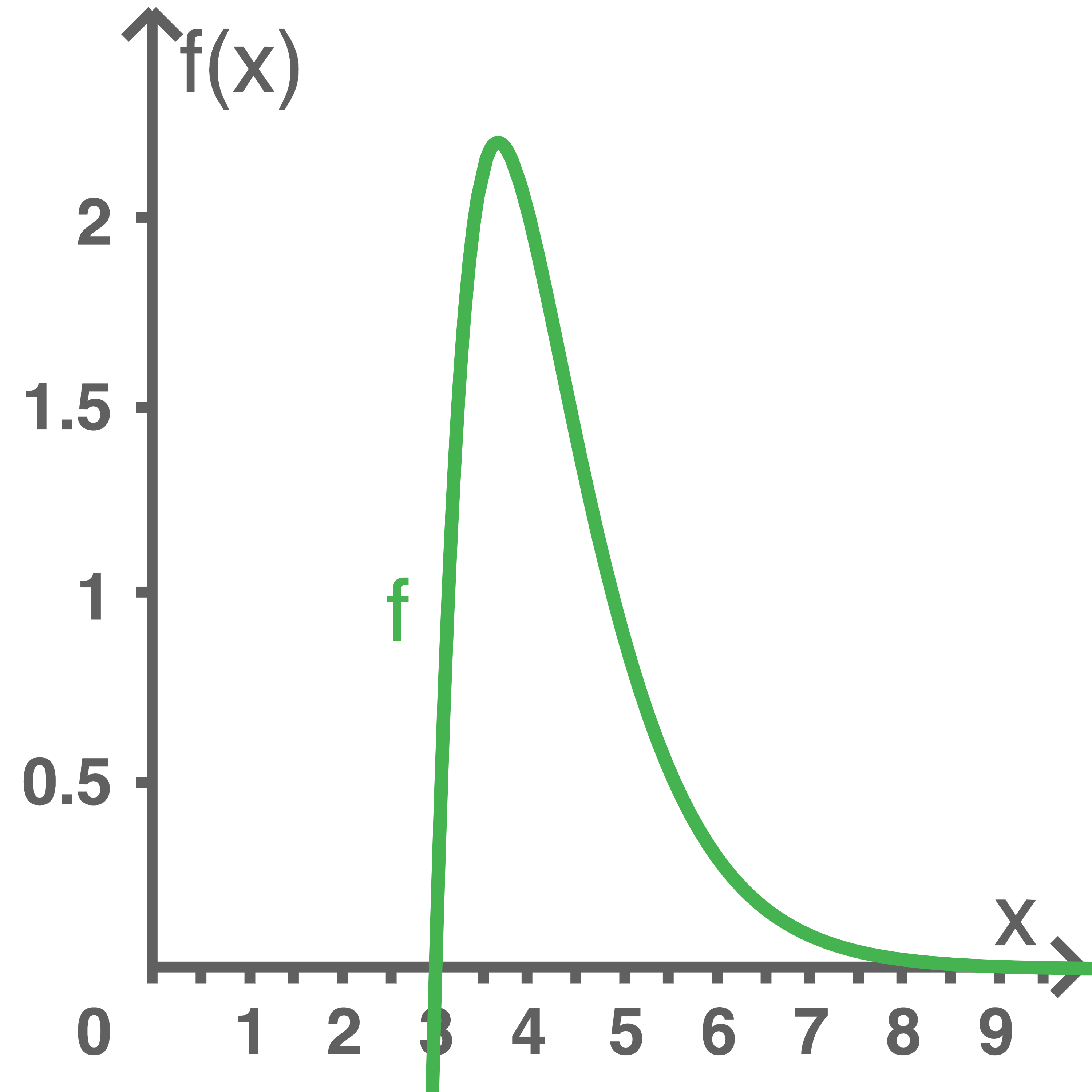
 Der Graph der Funktion
Der Graph der Funktion  ist in Abbildung 1 dargestellt.
ist in Abbildung 1 dargestellt.
 und
und  ist die Funktionenschar
ist die Funktionenschar  gegeben durch die Gleichung
gegeben durch die Gleichung 

Es gilt
 hat den Hochpunkt
hat den Hochpunkt  mit
mit 

Abbildung 1
a)
(1)
Der Graph der Funktion  hat genau einen Schnittpunkt
hat genau einen Schnittpunkt  mit der
mit der  -Achse und genau einen Hochpunkt
-Achse und genau einen Hochpunkt 
Gib die Koordinaten von an.
an.
Ermittle die Koordinaten des Punktes
Gib die Koordinaten von
Ermittle die Koordinaten des Punktes
(2)
Der Graph der Funktion  die
die  -Achse und die Gerade mit der Gleichung
-Achse und die Gerade mit der Gleichung  schließen eine Fläche ein.
schließen eine Fläche ein.
Bestimme den Inhalt dieser Fläche.
Bestimme den Inhalt dieser Fläche.
(3)
Gib den Wert von  für
für  und die geometrische Bedeutung dieses Wertes an.
und die geometrische Bedeutung dieses Wertes an.
(4)
Für jedes  sind
sind 
 und
und  die Eckpunkte eines Dreiecks.
die Eckpunkte eines Dreiecks.
(i)
Begründe, dass sich der Flächeninhalt des Dreiecks  in Abhängigkeit von
in Abhängigkeit von  mit der Gleichung
mit der Gleichung  berechnen lässt.
berechnen lässt.
(ii)
Begründe ohne weitere Rechnung, für welchen Wert von  der Flächeninhalt des Dreiecks
der Flächeninhalt des Dreiecks  maximal wird.
maximal wird.
(iii)
Bestimme alle Werte von  für die das Dreieck
für die das Dreieck  einen Flächeninhalt von
einen Flächeninhalt von  Flächeneinheiten hat.
Flächeneinheiten hat.
(3 + 2 + 2 + 6 Punkte)
b)
Für ein  mit
mit  ist der Punkt
ist der Punkt  gegeben. Der Graph der Funktion
gegeben. Der Graph der Funktion  ist die Tangente an den Graphen von
ist die Tangente an den Graphen von  im Punkt
im Punkt  Für
Für  wird der Graph von
wird der Graph von  betrachtet. Für
betrachtet. Für  wird der Graph von
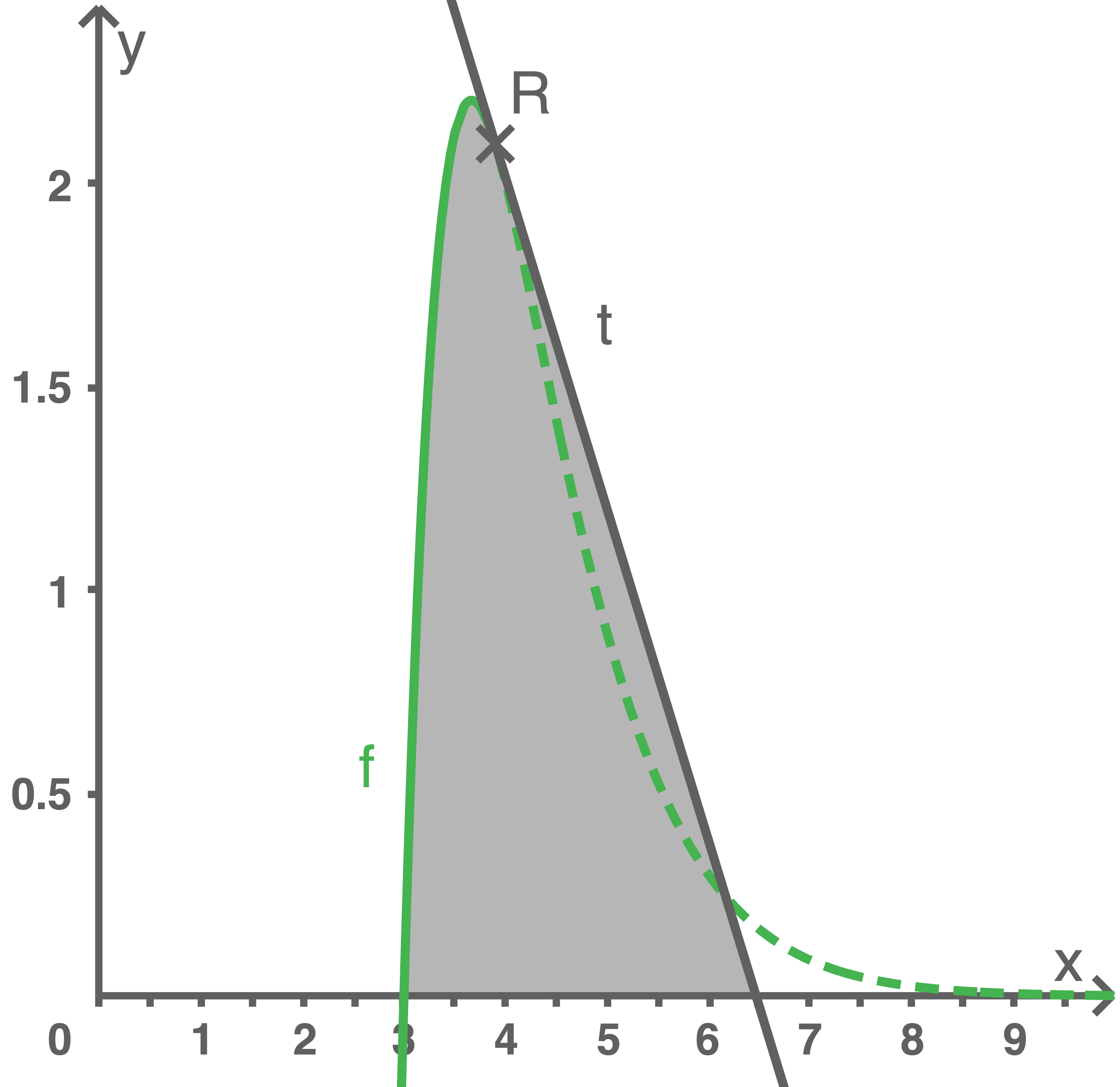
wird der Graph von  betrachtet. Abbildung 2 auf der folgenden Seite veranschaulicht diese Situation für das Beispiel
betrachtet. Abbildung 2 auf der folgenden Seite veranschaulicht diese Situation für das Beispiel 
Die betrachteten Graphen der Funktionen und
und  schließen mit der
schließen mit der  -Achse die in Abbildung 2 farbig dargestellte Fläche ein. Der Wert von
-Achse die in Abbildung 2 farbig dargestellte Fläche ein. Der Wert von  kann mithilfe der folgenden Bedingungen so bestimmt werden, dass diese Fläche einen Flächeninhalt von
kann mithilfe der folgenden Bedingungen so bestimmt werden, dass diese Fläche einen Flächeninhalt von  Flächeneinheiten hat:
Flächeneinheiten hat:





 wobei
wobei  die Nullstelle von
die Nullstelle von  ist.
ist.
Für Die betrachteten Graphen der Funktionen

Abbildung 2
(1)
(i)
Begründe die Wahl der Bedingungen  und
und 
(ii)
Erläutere die linke Seite der Gleichung in Bedingung 
(2)
Aus den Bedingungen folgt 
(i)
Es gilt:  Bestimme für
Bestimme für  rechnerisch eine Gleichung der Funktion
rechnerisch eine Gleichung der Funktion  deren Graph die Tangente an den Graphen von
deren Graph die Tangente an den Graphen von  im Punkt
im Punkt  ist.
ist.
(ii)
Ermittle die Nullstelle dieser Funktion 
(4 + 4 Punkte)
Es gilt
c)
(1)
Begründe, dass alle Graphen von Funktionen der Schar  nur einen Schnittpunkt mit der
nur einen Schnittpunkt mit der  -Achse haben.
-Achse haben.
(2)
Ohne Nachweis darf verwendet werden: 
Bestimme rechnerisch die Extremstelle und die Art des Extremums des Graphen von in Abhängigkeit von
in Abhängigkeit von 
 Zur Kontrolle: Die Extremstelle ist
Zur Kontrolle: Die Extremstelle ist ![\(x=3+\dfrac{1}{k}.\bigg]\)](https://mathjax.schullv.de/0f97269cf7b01f532aae5056662cc71429cc6d381186b2972fcd42158e8ec172?color=5a5a5a)
Bestimme rechnerisch die Extremstelle und die Art des Extremums des Graphen von
(3)
Die Funktion  mit
mit  ist eine Stammfunktion der Funktion
ist eine Stammfunktion der Funktion 
Für liegt zwischen der
liegt zwischen der  -Achse und dem Graphen der Funktion
-Achse und dem Graphen der Funktion  die nach rechts offene Fläche
die nach rechts offene Fläche 
Prüfe rechnerisch, ob der Inhalt der Fläche vom Parameter
vom Parameter  abhängt.
abhängt.
Der Graph der Funktion Für
Prüfe rechnerisch, ob der Inhalt der Fläche
(4)
Die Graphen der Funktionen  und
und  schneiden sich nur im Punkt
schneiden sich nur im Punkt  und in einem weiteren Punkt
und in einem weiteren Punkt 
(i)
Gib die Koordinaten des Hochpunktes des Graphen von  an und bestimme die Koordinaten des Schnittpunktes
an und bestimme die Koordinaten des Schnittpunktes  der Graphen von
der Graphen von  und
und 
(ii)
Skizziere mithilfe dieser Punkte den Graphen der Funktion  in Abbildung 3.
in Abbildung 3.
(5)
Für  ist der Graph der Funktion
ist der Graph der Funktion  in Abbildung 3 dargestellt.
Begründe anhand des Hochpunktes
in Abbildung 3 dargestellt.
Begründe anhand des Hochpunktes  ohne weitere Berechnung, ob der Wert von
ohne weitere Berechnung, ob der Wert von  größer oder kleiner ist als
größer oder kleiner ist als 
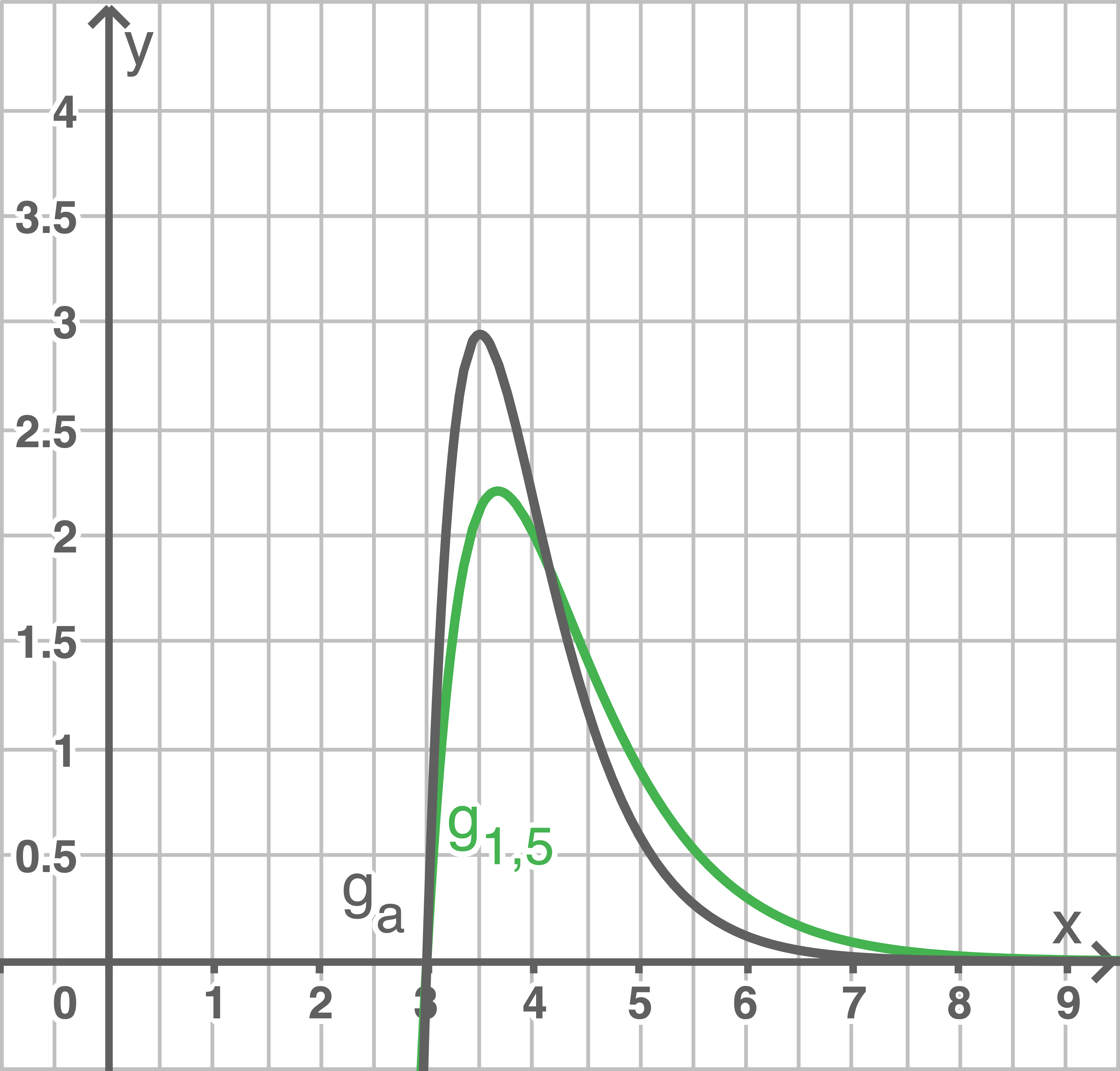

Abbildung 3
(2 + 7 + 4 + 4 + 2 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Aus der Abbildung kann  abgelesen werden. Die Koordinaten des Hochpunktes ergeben sich aus der graphischen Analyse mithilfe des GTRs
abgelesen werden. Die Koordinaten des Hochpunktes ergeben sich aus der graphischen Analyse mithilfe des GTRs 
(2)
(3)
(4)
(i)
Als Grundseite des Dreiecks  kann die Strecke
kann die Strecke  verwendet werden. Deren Länge ist
verwendet werden. Deren Länge ist  Längeneinheiten. Die Länge der zugehörigen Höhe ist durch
Längeneinheiten. Die Länge der zugehörigen Höhe ist durch  gegeben. Für den Flächeninhalt des Dreiecks gilt:
gegeben. Für den Flächeninhalt des Dreiecks gilt:

(ii)
Da der Flächeninhalt immer der dreifache Wert des Funktionswertes  und der Funktionswert im Hochpunkt maximal ist, wird der Flächeninhalt des Dreiecks
und der Funktionswert im Hochpunkt maximal ist, wird der Flächeninhalt des Dreiecks  für
für  maximal.
maximal.
(iii)
b)
(1)
(i)
Die Bedingungen  und
und  stellen sicher, dass es sich bei der Funktion
stellen sicher, dass es sich bei der Funktion  um die Tangente an den Graphen der Funktion
um die Tangente an den Graphen der Funktion  im Punkt
im Punkt  handelt bzw. dass der Übergang „knickfrei“ erfolgt.
handelt bzw. dass der Übergang „knickfrei“ erfolgt.
(ii)
Mit dem ersten Integral wird der Inhalt der Fläche zwischen dem Graphen von  und der
und der  -Achse über dem Intervall
-Achse über dem Intervall ![\([3 ; z]\)](https://mathjax.schullv.de/304fd135275f451be4795ad4f0e1fed8e9b2e281bf6a13548066fce372275896?color=5a5a5a) berechnet. Mit dem zweiten Integral wird der Inhalt der Fläche zwischen dem Graphen von
berechnet. Mit dem zweiten Integral wird der Inhalt der Fläche zwischen dem Graphen von  und der
und der  -Achse über dem Intervall
-Achse über dem Intervall ![\([z;c]\)](https://mathjax.schullv.de/4c89e9b1f81f468f4235db26200dbe0940d265411b9574ac3214f4eb2b687287?color=5a5a5a) berechnet, wobei
berechnet, wobei  die Nullstelle der Funktion
die Nullstelle der Funktion  ist. Die Addition ergibt den Flächeninhalt der in der Aufgabe beschriebenen Fläche.
ist. Die Addition ergibt den Flächeninhalt der in der Aufgabe beschriebenen Fläche.
(2)
(i)
(ii)
c)
(1)
(2)
Mit der Produkt- und Kettenregel ergibt sich:
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
 , da
, da  Somit befindet sich an der Stelle
Somit befindet sich an der Stelle  ein Hochpunkt.
ein Hochpunkt.
(3)
Der erste Summand wird von  dominiert. Mit
dominiert. Mit  gilt:
gilt:  Es folgt:
Es folgt:  Der Flächeninhalt der Fläche
Der Flächeninhalt der Fläche  beträgt somit, unabhängig vom Parameter
beträgt somit, unabhängig vom Parameter  ,
,  Flächeneinheiten.
Flächeneinheiten.
(4)
(i)
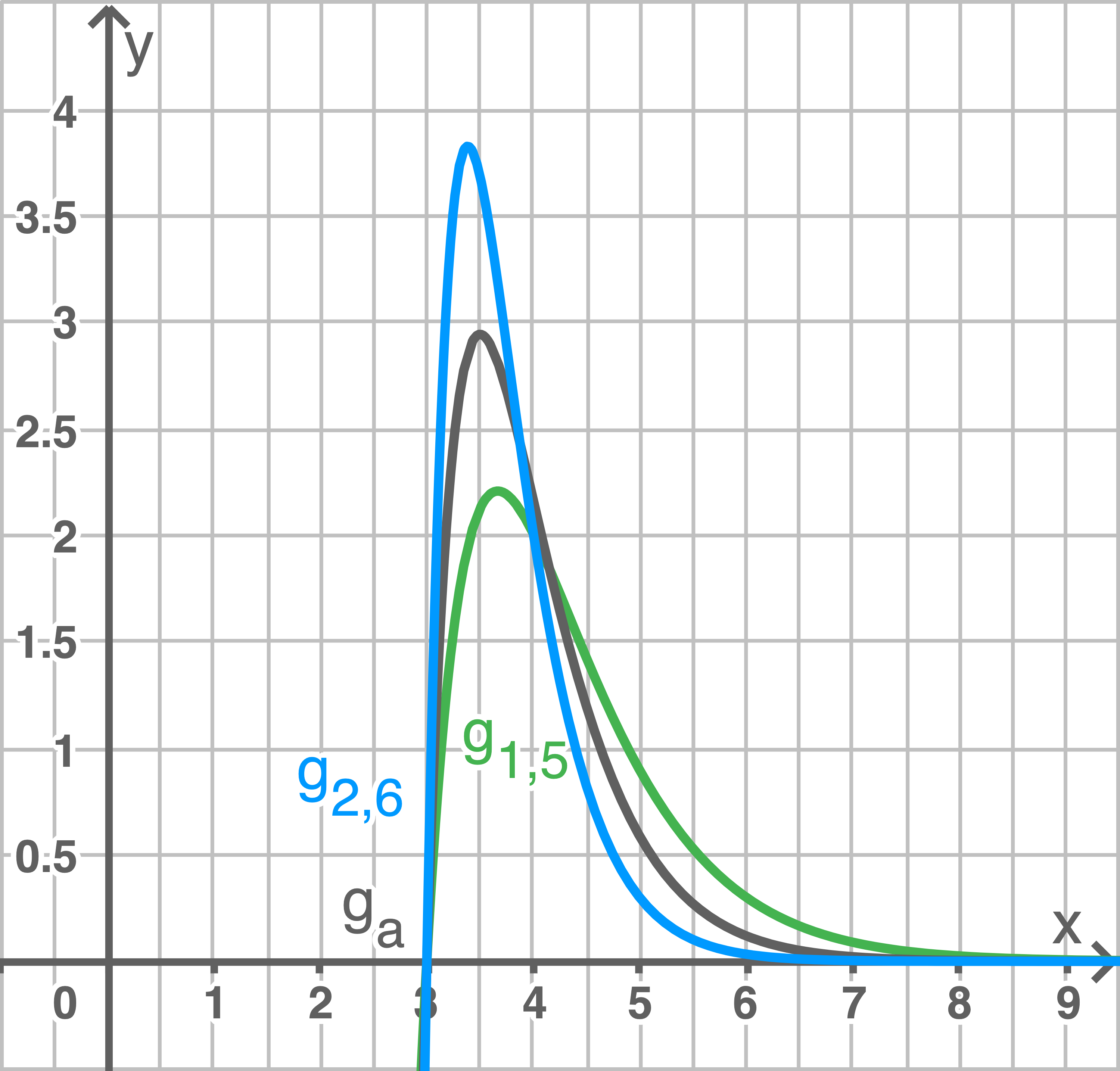
Mithilfe der graphischen Analyse des GTR folgt: der Hochpunkt des Graphen von  ist ungefähr
ist ungefähr  und der Schnittpunkt
und der Schnittpunkt  ungefähr
ungefähr 
(ii)
(5)
Die  -Koordinate von
-Koordinate von  ist größer als die
ist größer als die  -Koordinate des Hochpunktes des Graphen von
-Koordinate des Hochpunktes des Graphen von  Da die
Da die  -Koordinate des Hochpunktes linear mit
-Koordinate des Hochpunktes linear mit  wächst, muss der Parameter
wächst, muss der Parameter  größer sein als
größer sein als 