A - Hilfsmittelfreier Teil

Analysis - Niveau 1

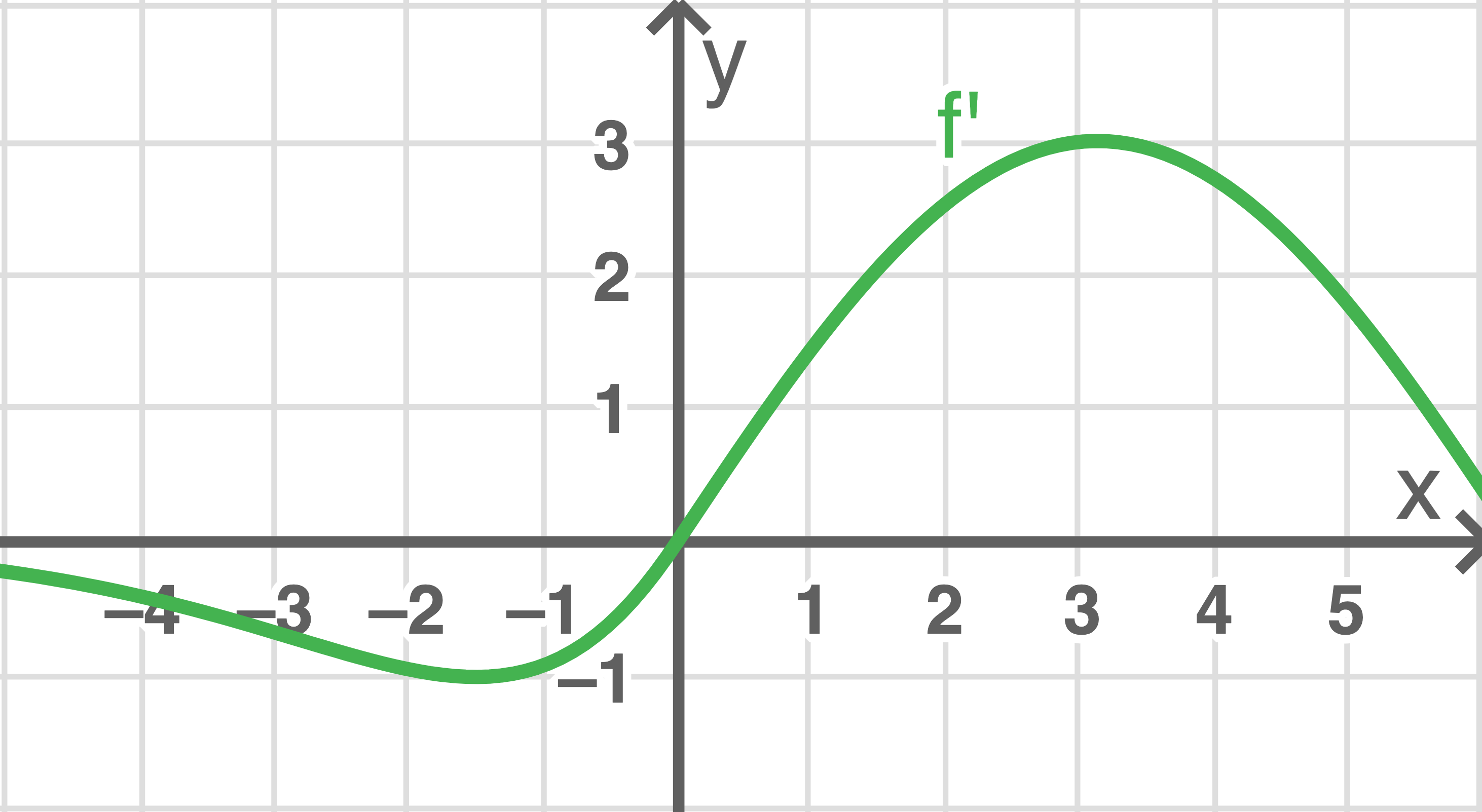
Die Abbildung zeigt den Graphen der ersten Ableitung $\(f$ einer Funktion $f.$ Entscheide, ob folgende Aussagen über die Funktion $f$ wahr sind:

$f$ wächst monoton im Intervall $[-1;1].$

$f$ hat mindestens ein relatives Minimum.

Es gilt: $f(4)\gt f(-4)$

(5 BE)

Lineare Algebra/Analytische Geometrie - Niveau 1

2.1

Gegeben sind die Vektoren $\overrightarrow{a}=\left(\begin{array}{c} 1 \\c\\ 2 \end{array}\right)$ und $\overrightarrow{b}=\left(\begin{array}{c} c+4 \\ -1 \\2 \end{array}\right)$ mit $c \in \mathbb{R}$ .

Begründe, dass $\overrightarrow{a}$ und $\overrightarrow{b}$ nicht kollinear sind.

(2 BE)

2.2

Berechne den Wert für $c$ so, dass $\,\bigg \vert \, \overrightarrow{a}\,\bigg \vert \,=\,\bigg \vert \,\overrightarrow{b}\,\bigg \vert \,$ gilt.

(3 BE)

Stochastik - Niveau 1

3.1

Eine Basketballspielerin trifft den Korb beim Freiwurf immer mit der gleichen Wahrscheinlichkeit von $90\,\%.$

Gib einen Term an, mit dem die Wahrscheinlichkeit berechnet werden kann, dass die Basketballspielerin bei drei Freiwürfen den Korb genau zweimal trifft.

(2 BE)

3.2

Eine andere Basketballspielerin trifft den Korb beim Freiwurf immer mit der gleichen Trefferwahrscheinlichkeit $p.$

Berechne diese Trefferwahrscheinlichkeit, wenn sie bei zwei Freiwürfen mit einer Wahrscheinlichkeit von $84\,\%$ den Korb mindestens einmal trifft.

(3 BE)

Stochastik - Niveau 2

4.1

Die sechs Seitenflächen eines Würfels sind mit den Augenzahlen $1,$ $1,$ $2,$ $2,$ $2$ und $4$ beschriftet. Die Zufallsvariable $X$ bezeichne die geworfene Augenzahl.

Berechne $E(X).$

(2 BE)

4.2

Fünf der sechs Seitenflächen eines anderen Würfels sind mit den Augenzahlen $1,$ $1,$ $2,$ $2$ und $4$ beschriftet. Der Erwartungswert für die Summe der geworfenen Augenzahlen bei $150$ Würfen beträgt $375$ .

Berechne die fehlende Augenzahl.

(3 BE)

Analysis - Niveau 1

Die Aussage ist falsch.

Wenn die Funktion $f$ im Intervall $[-1;1]$ monoton wachsen würde, dann wäre die Steigung immer positiv. Die Ableitungsfunktion müsste also im gesamten Intervall oberhalb der $x$ -Achse liegen.
Am Graphen der Ableitungsfunktion $\(f$ ist erkennbar, dass $\(f$ im Intervall $[-1,0]$ ist. Die Funktion fällt also und ist somit nicht monoton wachsend.

Die Aussage ist wahr.

Extrempunkte können an den Nullstellen der Ableitung erkannt werden, hier also bei $x=0$ . Für einen Tiefpunkt muss es einen Vorzeichenwechsel von Minus nach Plus geben. Dies ist hier ebenfalls der Fall. Somit hat $f$ bei $x=0$ eine relatives Minimum.

Die Aussage ist wahr.

Um von $\(f$ auf $f$ zu kommen, musst du die Funktion integrieren beziehungsweise die Fläche unter der Kurve betrachten. Da die Fläche oberhalb der $x$ -Achse für $0\leq x \leq 4$ deutlich größer ist als die Fläche unterhalb der $x$ -Achse für $-4 \leq x \leq 0$ , ist die Funktion $f$ im gesamten Intevall von $-4 \le x \leq 4$ gewachsen. Also gilt $f(4)>f(-4)$ .

Lineare Algebra/Analytische Geometrie - Niveau 1

2.1

Wenn die beiden Vektoren kollinear wären, müsste $\vec{b}$ ein vielfaches von $\vec{a}$ sein.:

$\begin{array}[t]{rll} \vec{a}&=&n\cdot \vec{b} \\[5pt] \left(\begin{array}{c} 1 \\c\\ 2 \end{array}\right)&=&n\cdot \left(\begin{array}{c} c+4 \\ -1 \\2 \end{array}\right) \end{array}$

Aus der dritten Zeile ergibt sich $n=1$ . Damit folgt aus der zweiten Zeile, dass $c=-1$ wäre.

Einsetzen von $c=-1$ in die erste Zeile ergibt jedoch:

$1\neq-1+4$

Somit sind die beiden Vektoren nicht kollinear.

2.2

Rechenweg anzeigen

$c=-2$

Stochastik - Niveau 1

3.1

Die Wahrscheinlichkeiten sind Binomialverteilt, da die Basketballspielerin jeden Korb mit der gleichen Wahrscheinlichkeit trifft und die Würfe unabhängig voneinander sind. $n=3$ ist die Anzahl der Würfe, $k=2$ ist die Anzahl der Treffer und $p=0,9$ ist die Trefferwahrscheinlichkeit. Damit gilt für den Term:

$P(X=k)=\left(\begin{array}{c} n\\k \end{array}\right) \cdot p^k \cdot (1-p)^{n-k}$

$P(X=2)=\left(\begin{array}{c} 3\\2 \end{array}\right)\cdot 0,9^2\cdot0,1$

3.2

Für $n=2$ gilt:

$P(x\geq 1)=1-P(X=0)=0,84$

Mit der Bernoulli-Formel gilt:

$\begin{array}[t]{rll} P(X=0)&=&\left(\begin{array}{c} 2\\0 \end{array}\right)\cdot p^0 \cdot (1-p)^2 \\[5pt] &=&(1-p)^2 \end{array}$

Durch Einsetzen in die obere Geichung folgt:

$\begin{array}[t]{rll} 1-(1-p)^2&=&0,84 &\quad \scriptsize \mid\; -1\\[5pt] -(1-p)^2&=&-0,16 &\quad \scriptsize \mid\; :(-1)\\[5pt] (1-p)^2&=&0,16 &\quad \scriptsize \mid\; \sqrt{} \\[5pt] 1-p&=&\pm 0,4 \\[5pt] p_1&=& 0,6 \\[5pt] p_2&=&1,4 \end{array}$