B2 - Analysis

Gegeben sei die Funktionenschar $f_b$ mit $f_b(t)=\dfrac{1}{100} \cdot (0,5t^2+2t)\cdot b \cdot \mathrm e^{-0,02t},$ $b\in \mathbb{R}, b\gt 0.$

1.1

Berechne die Nullstellen der Funktionen der Schar.

(3 BE)

1.2

Beschreibe die Bedeutung des Parameters $b$ für die Graphen der Schar.
Berechne alle Extrempunkte der Graphen der Schar.
Die Funktionsgleichung der zweiten Ableitung

Ableitung anzeigen

darf ohne Nachweis verwendet werden.

[Zur Kontrolle: Die Hochpunkte der Schar haben die gerundeten Koordinaten $H(98,04\mid 7,04b).$ ]

(8 BE)

1.3

Untersuche das Grenzverhalten der Funktionen der Schar für $t \rightarrow+\infty$ und $t \rightarrow-\infty.$

(4 BE)

Ein hessischer Radiosender startet anlässlich einer Naturkatastrophe eine Spendenaktion. Die Zuschauer haben bei dieser Spendenaktion die Möglichkeit, über eine Spendenhotline telefonisch einen Betrag von $50 \,\text{€}$ zu spenden. Die Spendenhotline ist für einen Zeitraum von acht Stunden erreichbar.

2.1

Die Eingangsrate (in Anrufen pro Minute) lässt sich in guter Näherung durch eine Funktion der Funktionenschar $f_b$ aus Aufgabe 1 modellieren. Dabei beschreibt $t$ die Zeit in Minuten seit Beginn der Spendenaktion.

2.1.1

Nach einer Stunde beträgt die Eingangsrate 17 Anrufe pro Minute.
Bestimme, gerundet auf zwei Nachkommastellen, den zugehörigen Wert des Parameters $b$ .

(2 BE)

Im Folgenden soll die Eingangsrate (in Anrufen pro Minute) in Abhängigkeit von der Zeit $t$ (in Minuten seit Beginn der Spendenaktion) durch die Funktion $f$ mit
$f(t)=0,03 \cdot\left(0,5t^{2}+2 t\right) \cdot \mathrm{e}^{-0,02 \mathrm{t}}=f_3(t)$
der Funktionenschar aus Aufgabe 1 modelliert werden. Der Graph der Funktion $f$ ist für $t \geq 0$ im Material 1 dargestellt.

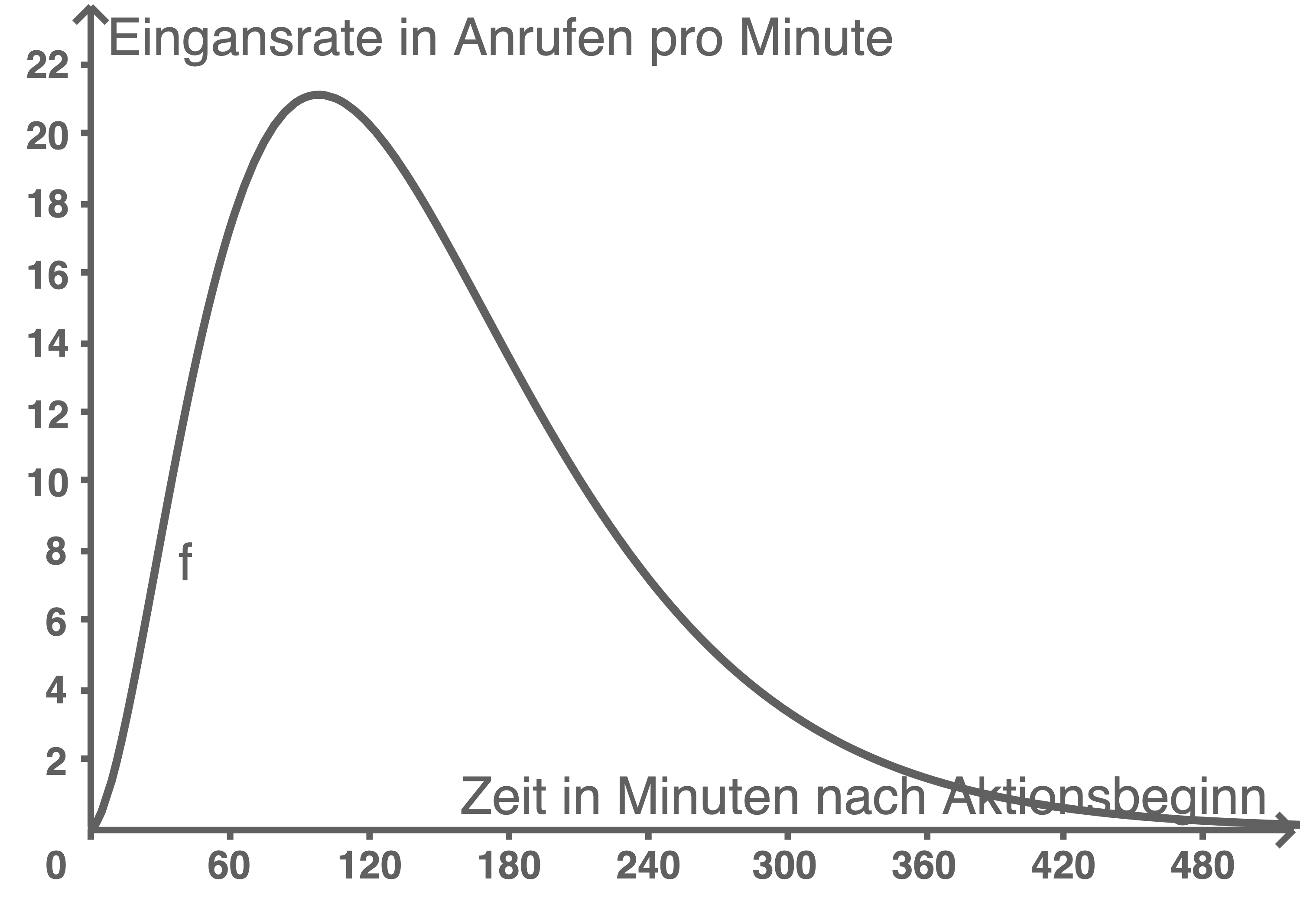
hessen mathe abi lk wtr 2022 vorschlag b2 abbildung 1

Material 1
Graph der Näherungsfunktion $f$

2.1.2

Vergleiche die Eingangsraten nach zwei Stunden und nach acht Stunden im Sachzusammenhang.

(2 BE)

2.1.3

Ermittle ohne Verwendung des Graphen die maximale Eingangsrate gemäß der vorgenommenen Modellierung.

(2 BE)

2.1.4

Bestimme, gerundet auf zwei Nachkommastellen, den Wert von $t$ , für welchen die Krümmung des Graphen der Funktion $f$ von einer Rechts- in eine Linkskrümmung wechselt.
Erläutere die Bedeutung dieses Werts im Sachzusammenhang.

(4 BE)

2.1.5

Bestimme die minimale Eingangsrate im Zeitraum $[40;240]$ .

(4 BE)

2.2.1

Berechne mithilfe eines geeigneten Formansatzes eine Stammfunktion $F$ von $f$ .
[Zur Kontrolle: $F(t)=(-0,75t^2-78t-3900) \cdot \mathrm e^{-0,02t}$ ist die Gleichung einer möglichen Stammfunktion $F$ .]

(6 BE)

2.2.2

Bestimme den Wert des Terms $50 \cdot \displaystyle\int_{0}^{480}f(t)\;\mathrm dt.$
Erläutere die Bedeutungen des Terms und des berechneten Werts im Sachzusammenhang.

(3 BE)

2.2.3

Für jede Stammfunktion $F$ von $f$ und für jede reelle Zahl $k>600$ gilt: $F(k)-F(0) \approx \displaystyle\int_{0}^{600}f(t)\;\mathrm dt$ . Deute diesen Sachverhalt geometrisch.

(3 BE)

Bei der Spendenaktion aus Aufgabe 2 können in der Hotline ohne entstehende Wartezeiten maximal 15 Anrufe pro Minute bearbeitet werden. Wird diese Maximalzahl überschritten, werden die eingehenden Telefonnummern registriert. Sobald wieder freie Apparate zur Verfügung stehen, werden die Anrufer mittels einer automatischen Rückruffunktion kontaktiert. Im Modell wird davon ausgegangen, dass alle mittels Rückruffunktion kontaktierten Anrufer direkt erreichbar sind.

3.1

Erläutere die Bedeutung der im Material 2 eingezeichneten Fläche im Sachzusammenhang.
Bestimme den Inhalt dieser Fläche.

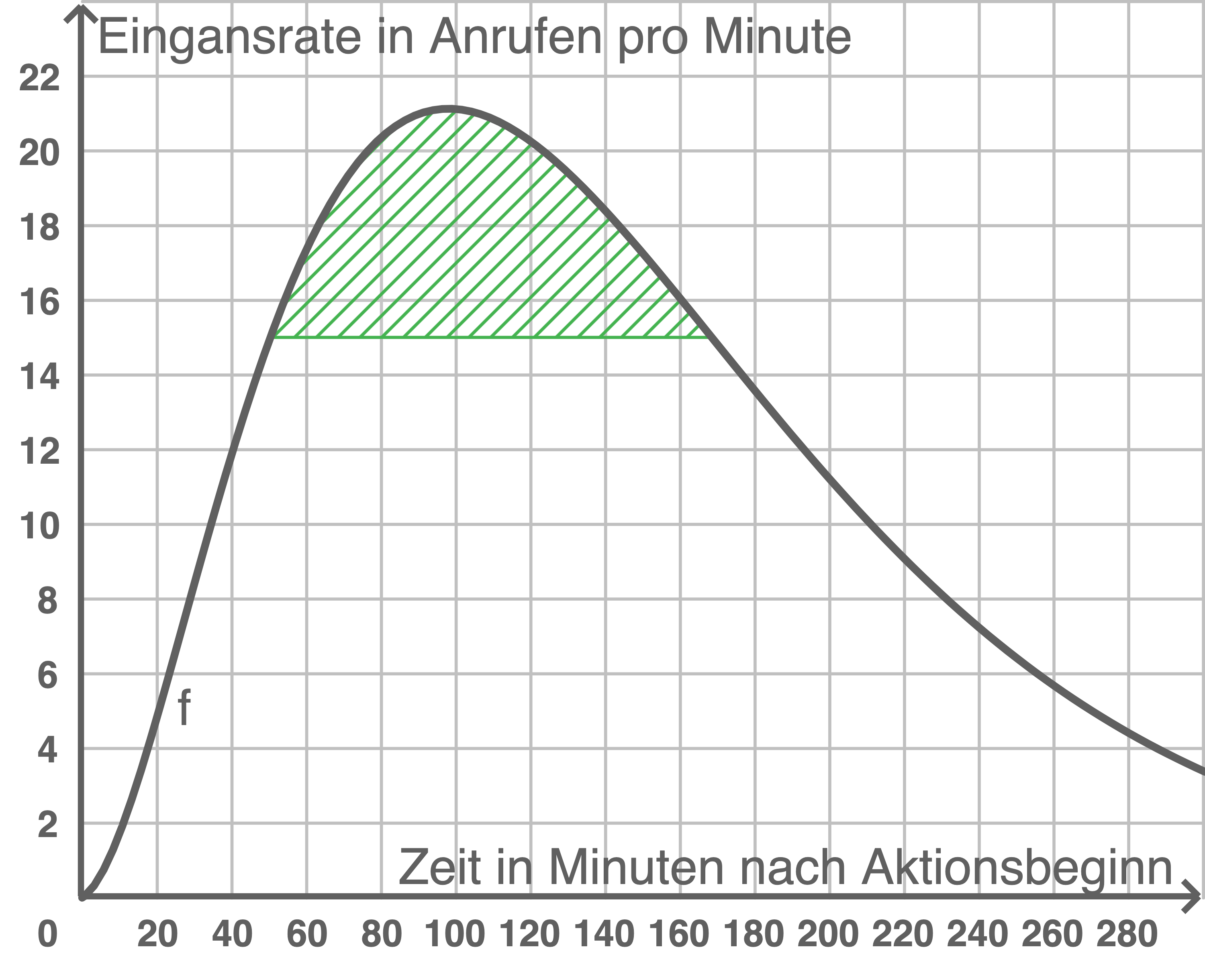
hessen mathe abi lk wtr 2022 vorschlag b2 abbildung 2

Material 2
Ausschnitt aus dem Graphen der Näherungsfunktion

(6 BE)

3.2

Ab dem Zeitpunkt $t=50$ werden Anrufer für automatische Rückrufe registriert.
Bestimme, bis zu welchem Zeitpunkt es anschließend dauert, alle Rückrufe zu tätigen.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$\begin{array}[t]{rll} f_b(t)&=&0 & \\[5pt] \dfrac{1}{100} \cdot (0,5t^2+2t)\cdot b \cdot \mathrm e^{-0,02t}&=&0 & \\[5pt] \end{array}$

Da $\mathrm e^{-0,02t}\gt 0$ und $b\gt 0$ , folgt:

$\begin{array}[t]{rll} \dfrac{1}{100} \cdot (0,5t^2+2t)&=& 0&\quad \scriptsize \mid\; \cdot 100 \\[5pt] t\cdot (0,5t+2)&=& 0& \\[5pt] \end{array}$

Somit ergeben sich die Nullstellen $t=0$ und $t=-4.$

1.2

Bedeutung des Parameters $b$

In der Aufgabenstellung ist $b \gt 0$ definiert. Für $b \gt 0$ verläuft der Graph oberhalb der $x$ -Achse. Je größer der Parameter $b,$ desto mehr wird der Graph der Schar in $y$ -Richtung gestreckt.

Erste Ableitung bestimmen

Anwendung der Produkt- und Kettenregel ergibt:

Ableitung anzeigen

Notwendige Bedingung für Extremstellen anwenden

$\( f$

Rechnung anzeigen

Da $\mathrm e^{-0,02t}\gt 0$ und $b\gt 0$ , folgt mit dem Satz vom Nullprodukt:

$-t^2+96t+200=0$

Mit dem solve-Befehl des CAS folgt:

$t_1\approx 98,04$ und $t_2 \approx -2,04$

Hinreichende Bedingung für Extremstellen prüfen

Rechenweg anzeigen

$\( f_b$

Rechenweg anzeigen

$\( f_b$

Ermitteln der Extrempunkte

$f_b(-2,04)\approx -0,02b$

Rechenweg anzeigen

Da $b \gt 0$ und $\(f_b$ gilt, besitzen die Graphen der Schar im Punkt $T(-2,04|-0,02b )$ einen Tiefpunkt.

$f_b(98,04)\approx 7,04b$

Rechenweg anzeigen

Da $b \gt 0$ und $\(f_b$ gilt, besitzen die Graphen der Schar im Punkt $H(98,04 \mid 7,04b )$ einen Hochpunkt.

1.3

Es gilt $\lim\limits_{t\to +\infty}f_b(t)=0,$ da der quadratische Term langsamer gegen unendlich strebt als die Exponentialfunktion gegen null.

Für $t\rightarrow+\infty$ gilt folglich $f_b(t)\rightarrow 0.$

Es gilt $\lim\limits_{t\to -\infty} f_b(t)=+\infty ,$ da sowohl der quadratisch Term als auch die Exponentialfunktion gegen unendlich streben.

Für $t\rightarrow+\infty$ gilt folglich $f_b(t)\rightarrow +\infty.$

2.1.1

$b \approx 2,94$

Rechenweg anzeigen

2.1.2

Nach zwei Stunden ist die Eingansrate der Anrufe pro Minute sehr hoch. Während zu diesem Zeitpunkt etwa 20 bis 21 mal pro Minute angerufen wird, gehen nach acht Stunden nur noch zwischen 0 und einem Anruf ein.

2.1.3

In 1.2 wurden bereits die Koordinaten des Hochpunkts der Schar in Abhängigkeit von $b$ ermittelt.

Durch Einsetzen von $b=3$ folgt:

$f_3(98,04)=7,04\cdot 3= 21,12$

Die maximale Eingansrate beträgt somit 21,12 Anrufe pro Minute.

2.1.4

Der Wechsel von einer Rechts- in eine Linkskrümmung beschreibt einen Wendepunkt am Graphen von $f.$

Notwendige Bedingung für Wendestellen anwenden

$\( f$

Rechenweg anzeigen

Da $\mathrm e^{-0,02t}\gt0$ , gilt $(2t^2-392t+9200)=0.$

Mit der $pq$ -Formel ergibt sich:

$\begin{array}[t]{rll} t_{1/2}&=& 98 \pm \sqrt{\left(\dfrac{(-196)}{2}\right)^2-4600} \\[5pt] t_1&\approx& 27,26& \\[5pt] t_2&\approx & 168,74 \end{array}$

Aus dem Graphen von $f$ kann abgelesen werden, dass es sich bei $t_2=168,74$ um einen Wechsel von einer Rechts- in eine Linkskrümmung handelt.

Bedeutung des Werts von $t$

Der Wert von $t$ gibt den Zeitpunkt in Minuten seit Beginn der Spendenaktion an, zu welchem die Eingangsrate am stärksten abnimmt.

2.1.5

Da die Eingansrate im Intervall an den Intervallsgrenzen lokale Minima besitzt, müssen die beiden Randwerte verglichen werden:

Rechenweg anzeigen

$f(40) \approx 11,86$

Rechenweg anzeigen

$f(240)\approx 7,23$

Die minimale Eingansrate im Zeitraum $[20;240]$ beträgt somit $7,23.$

2.2.1

$f(t)=\dfrac{3}{100} \cdot (0,5t^2+2t) \cdot \mathrm e^{-0,02t}$

Formansatz: $F(t)=\dfrac{3}{100}\cdot (at^2+bt+c)\cdot e^{-0,02t}$ und $\(F$

Produktregel: $\(F$

Aus $f(t)$ ergeben sich:

$\(u(t)=at^2+bt+c \text { mit } u$

$\(v(t)=\mathrm{e}^{-0,02 t} \text { mit } v$

Einsetzen in $\(F$ :

Rechnung anzeigen

Somit gilt:

$\text{I}: -0,02a=0,5$

$\text{II}: -0,02b+2a=2$

$\text{III}: b-0,02c=0$

Aus $\text{I}$ folgt $a=-25$ . Durch Einsetzen von $a$ in $\text{II}$ ergibt sich $b=-2600. \; \text{III}$ führt zu $c=-130000.$

Somit ergibt sich eine Stammfunktion $F$ mit:

Rechenweg anzeigen

$F(t)=(-0,75t^2+78t+3900)\cdot e^{-0,02t}$

2.2.2

Wert des Terms berechnen

$50 \cdot \displaystyle\int_{0}^{480} f(t)\;\mathrm dt \approx 195445,18$

Rechenweg anzeigen

Term deuten

Der Wert des Integrals entspricht der Anzahl der Anrufe innerhalb der acht Stunden nach Beginn der Spendenaktion. Pro Anruf werden $50\,€$ gespendet, der berechnete Wert des Terms gibt somit also den Gesamtwert des gespendeten Geldes in Euro an.

3.1

Eingezeichnete Fläche deuten

Die eingezeichnete Fläche entspricht der Anzahl der Anrufe, welche nicht sofort bearbeitet werden können und erst später durch einen Rückruf kontaktiert werden.

Flächeninhalt bestimmen

Der Zeitraum, zu welchen mehr als 15 Anrufe eingehen, ergibt sich zu:

$\begin{array}[t]{rll} f(t)&=& 15 \\[5pt] 0,03\cdot (0,5 t^2+2t) \cdot \mathrm e^{-0,02t}&=& 15 \end{array}$

Mit dem solve-Befehl des CAS folgt $t_1 \approx 50,37$ und $t_2 \approx 168,45.$

Durch Eingabe in den CAS folgt der Inhalt der Fläche mit:

$\displaystyle\int_{50,37}^{168,45}f(t)-15\;\mathrm dt$ $=\displaystyle\int_{50,37}^{168,45}0,03 \cdot (0,5\cdot t^2+2t)\cdot \mathrm e^{-0,02\cdot t}-15\;\mathrm dt$ $\approx 463,35 \;\text{[FE]}$

Es können folglich 463 Anrufe nicht sofort bearbeitet werden.

3.2

$15 \cdot (k-50)= \displaystyle\int_{50}^{k}f(t)\;\mathrm dt$ mit $k\gt 50$
Mit dem solve-Befehl des CAS folgt $k \approx 260.$

260 Minuten nach Beginn der Spendenaktion wurden alle registrierten Telefonnnummern zurückgerufen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?