C1 - Stochastik
Im Folgenden werden mit „Internetnutzer“ alle privaten Internetnutzerinnen und Internetnutzer in Deutschland ab einem Alter von 10 Jahren bezeichnet.
28 % der Internetnutzer telefonieren über das Internet
Wiesbaden -
1
Im Jahr 2013 wird für eine weitere Untersuchung über das Nutzungsverhalten im Internet eine große Anzahl zufällig ausgewählter Internetnutzer befragt.
1.1
Bestimme die Wahrscheinlichkeit, dass unter den ersten zehn befragten Personen
- genau drei Personen dabei sind, die das Internet für Telefonate nutzen,
- höchstens drei Personen dabei sind, die das Internet für Telefonate nutzen.
(5 BE)
1.2
Von zehn der zufällig ausgewählten Internetnutzer weiß man, dass genau zwei das Internet für Telefonate nutzen. Die zehn Personen werden nacheinander in zufälliger Reihenfolge befragt.
Bestimme die Wahrscheinlichkeit, dass unter den ersten drei Befragten genau einer dabei ist, der das Internet für Telefonate nutzt.
Bestimme die Wahrscheinlichkeit, dass unter den ersten drei Befragten genau einer dabei ist, der das Internet für Telefonate nutzt.
(5 BE)
2
Der Artikel über Internettelefonate in Deutschland enthält keine Angaben darüber, wie viel Prozent der Internetnutzer im Jahr 2013
- das Internet für Telefonate nutzen und im Alter von 25 bis 54 Jahren sind,
- 10 bis 24 Jahre alt sind.
(7 BE)
3
Schon im Frühjahr 2014 ist man davon überzeugt, dass der Anteil der Internetnutzer, die das Internet zum Telefonieren nutzen, über  liegt und sich damit im Vergleich zu 2013 erhöht hat. Zur Überprüfung dieser Hypothese will man einen Test auf der Basis einer zufällig ausgewählten Stichprobe von 50 Internetnutzern durchführen.
liegt und sich damit im Vergleich zu 2013 erhöht hat. Zur Überprüfung dieser Hypothese will man einen Test auf der Basis einer zufällig ausgewählten Stichprobe von 50 Internetnutzern durchführen.
Binomialsummenfunktion
3.1
Entwickle einen Hypothesentest mit einem Signifikanzniveau von  unter Angabe einer Entscheidungsregel.
unter Angabe einer Entscheidungsregel.
(7 BE)
3.2
Angenommen, der Anteil  der Internetnutzer, die das Internet zum Telefonieren nutzen, hat sich im Frühjahr 2014 im Vergleich zu 2013 tatsächlich erhöht.
Bei dem folgenden Funktionsgraphen wird in Abhängigkeit von
der Internetnutzer, die das Internet zum Telefonieren nutzen, hat sich im Frühjahr 2014 im Vergleich zu 2013 tatsächlich erhöht.
Bei dem folgenden Funktionsgraphen wird in Abhängigkeit von  die Wahrscheinlichkeit
die Wahrscheinlichkeit  dargestellt, bei einem zweiten Test zur Überprüfung derselben Hypothese mit dem Stichprobenumfang der Länge
dargestellt, bei einem zweiten Test zur Überprüfung derselben Hypothese mit dem Stichprobenumfang der Länge  und einem im Vergleich zu Aufgabe 3.1 veränderten Signifikanzniveau
und einem im Vergleich zu Aufgabe 3.1 veränderten Signifikanzniveau  einen Fehler 2. Art zu begehen (Operationscharakteristik).
einen Fehler 2. Art zu begehen (Operationscharakteristik).
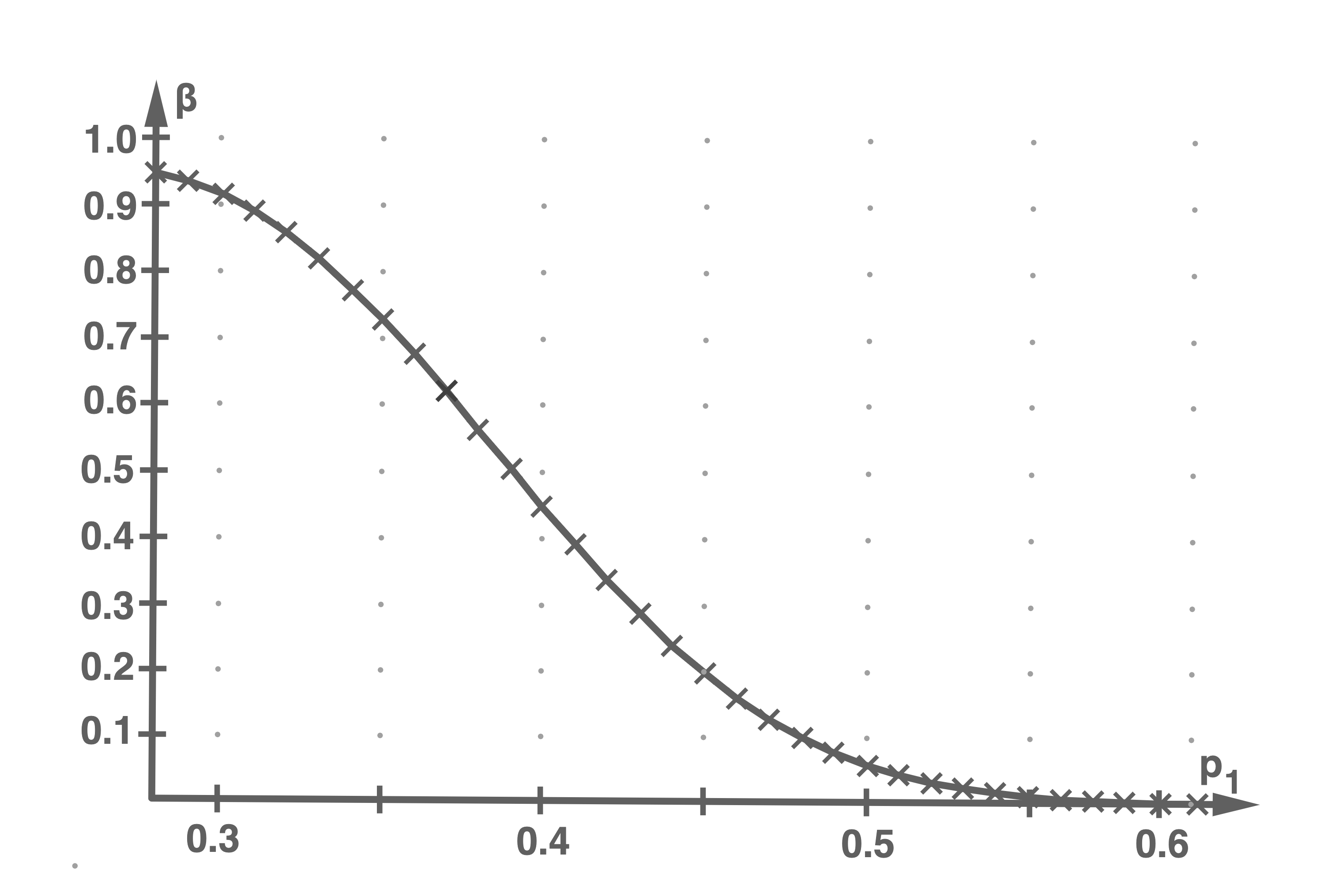 Gib
Gib  bei diesem Test mithilfe der Abbildung an, wenn der tatsächliche Anteil
bei diesem Test mithilfe der Abbildung an, wenn der tatsächliche Anteil  der Internetnutzer, die das Internet im Frühjahr 2014 zum Telefonieren nutzen,
der Internetnutzer, die das Internet im Frühjahr 2014 zum Telefonieren nutzen,  % beträgt, und erläutere den Wert im Sachzusammenhang.
Bestimme den zu diesem Test zugehörigen Ablehnungsbereich.
% beträgt, und erläutere den Wert im Sachzusammenhang.
Bestimme den zu diesem Test zugehörigen Ablehnungsbereich.

(6P)
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
|
1
|
n | p | |||||
|
2
|
k | 0,20 | 0,28 | 0,3 | 0,35 | 0,40 | |
|
3
|
50 | 0 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
|
4
|
1 | 0,0002 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | |
|
5
|
2 | 0,0013 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | |
|
6
|
3 | 0,0057 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | |
|
7
|
4 | 0,0185 | 0,0005 | 0,0002 | 0,0000 | 0,0000 | |
|
8
|
5 | 0,0480 | 0,0019 | 0,0007 | 0,0001 | 0,0000 | |
|
9
|
6 | 0,1034 | 0,0059 | 0,0025 | 0,0002 | 0,0000 | |
|
10
|
7 | 0,1904 | 0,0158 | 0,0073 | 0,0008 | 0,0001 | |
|
11
|
8 | 0,3073 | 0,0365 | 0,0183 | 0,0025 | 0,0002 | |
|
12
|
9 | 0,4437 | 0,0740 | 0,0402 | 0,0067 | 0,0008 | |
|
13
|
10 | 0,5836 | 0,1337 | 0,0789 | 0,0160 | 0,0022 | |
|
14
|
11 | 0,7107 | 0,2183 | 0,1390 | 0,0342 | 0,0057 | |
|
15
|
12 | 0,8139 | 0,3251 | 0,2229 | 0,0661 | 0,0133 | |
|
16
|
13 | 0,8894 | 0,4466 | 0,3279 | 0,1163 | 0,0280 | |
|
17
|
14 | 0,9393 | 0,5714 | 0,4468 | 0,1878 | 0,0540 | |
|
18
|
15 | 0,9692 | 0,6879 | 0,5692 | 0,2801 | 0,0955 | |
|
19
|
16 | 0,9856 | 0,7870 | 0,6839 | 0,3889 | 0,1561 | |
|
20
|
17 | 0,9937 | 0,8641 | 0,7822 | 0,5060 | 0,2369 | |
|
21
|
18 | 0,9975 | 0,9191 | 0,8594 | 0,6216 | 0,3356 | |
|
22
|
19 | 0,9991 | 0,9551 | 0,9152 | 0,7264 | 0,4465 | |
|
23
|
20 | 0,9997 | 0,9768 | 0,9522 | 0,8139 | 0,5610 | |
|
24
|
21 | 0,9999 | 0,9888 | 0,9749 | 0,8813 | 0,6701 | |
|
25
|
22 | 1,0000 | 0,9950 | 0,9877 | 0,9290 | 0,7660 | |
|
26
|
23 | 1,0000 | 0,9979 | 0,9944 | 0,9604 | 0,8438 | |
|
27
|
24 | 1,0000 | 0,9992 | 0,9976 | 0,9793 | 0,9022 | |
|
28
|
25 | 1,0000 | 0,9997 | 0,9991 | 0,9900 | 0,9427 | |
|
29
|
26 | 1,0000 | 0,9999 | 0,9997 | 0,9955 | 0,9686 | |
|
30
|
27 | 1,0000 | 1,0000 | 0,9999 | 0,9981 | 0,9840 | |
|
31
|
28 | 1,0000 | 1,0000 | 1,0000 | 0,9993 | 0,9924 | |
|
32
|
29 | 1,0000 | 1,0000 | 1,0000 | 0,9997 | 0,9966 | |
|
33
|
30 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9986 | |
|
34
|
31 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9995 | |
|
35
|
32 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9998 | |
|
36
|
33 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | |
|
37
|
34 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | |
|
38
|
35 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | |
1
1.1
Es handelt sich hierbei um eine Bernoulli-Kette mit Parametern  und
und  .
Die Zufallsvariable
.
Die Zufallsvariable  gibt an, wie viele der ersten zehn befragten Personen über das Internet telefonieren.
gibt an, wie viele der ersten zehn befragten Personen über das Internet telefonieren.  kann hier als binomialverteilt mit
kann hier als binomialverteilt mit  und
und  angenommen werden.
Wahrscheinlichkeit, dass genau drei Personen das Internet für Telefonate nutzen
Binomialverteilte Wahrscheinlichkeiten können mit dem CAS berechnet werden. Dazu muss in den Calculator-Modus gewechselt werden.
angenommen werden.
Wahrscheinlichkeit, dass genau drei Personen das Internet für Telefonate nutzen
Binomialverteilte Wahrscheinlichkeiten können mit dem CAS berechnet werden. Dazu muss in den Calculator-Modus gewechselt werden.
 ,
,  und
und  ergibt sich:
ergibt sich:
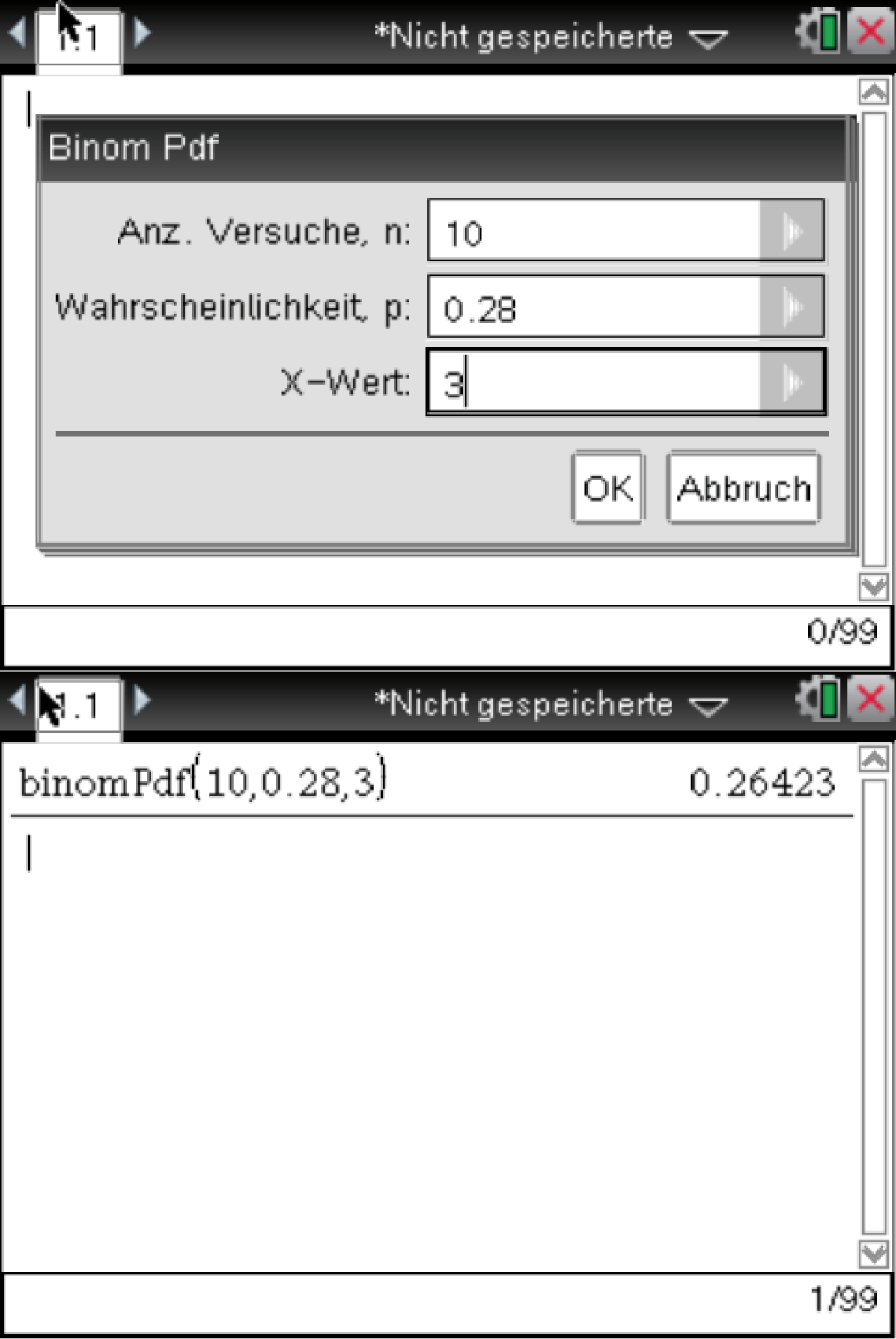 Es folgt
Es folgt  Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen genau drei Personen über das Internet telefonieren, beträgt somit etwa
Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen genau drei Personen über das Internet telefonieren, beträgt somit etwa  Wahrscheinlichkeit, dass höchstens drei Personen das Internet für Telefonate nutzen
Mit dem CAS ergibt sich analog zum ersten Ereignis:
Wahrscheinlichkeit, dass höchstens drei Personen das Internet für Telefonate nutzen
Mit dem CAS ergibt sich analog zum ersten Ereignis:
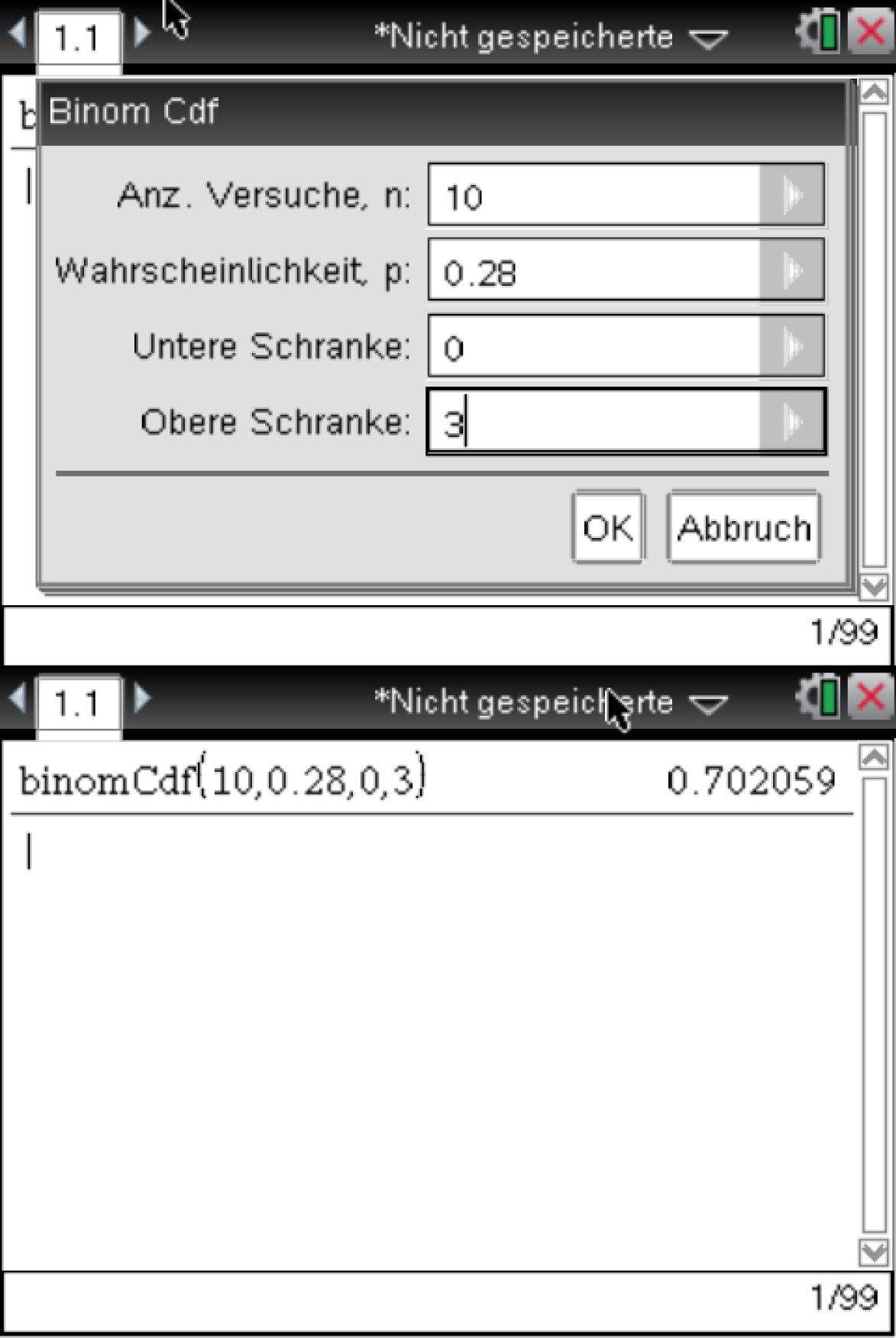 Es folgt also
Es folgt also  .
Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen höchstens drei Personen über das Internet telefonieren, beträgt somit
.
Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen höchstens drei Personen über das Internet telefonieren, beträgt somit 
menu  5
5  5
5  D: Binomial Pdf
D: Binomial Pdf
Nach Eingabe der Parameter 
menu  5
5  5
5  E: Binomial Cdf
E: Binomial Cdf

1.2
1. Schritt: Anzahl der Möglichkeiten, die Treffer und Nieten anzuordnen
Laut Aufgabenstellung nutzen zwei von zehn der befragten Personen das Internet für Telefonate. Somit gibt es in dieser Situation zwei Treffer und 8 Nieten.
Hierbei handelt es sich um das Ziehen aus einer ungeordneten Stichprobe ohne Zurücklegen.
Somit gibt es  Möglichkeiten, die Treffer und Nieten anzuordnen.
2. Schritt: Anzahl der Möglichkeiten, dass Ereignis
Möglichkeiten, die Treffer und Nieten anzuordnen.
2. Schritt: Anzahl der Möglichkeiten, dass Ereignis  gilt
Die 10 Befragten werden in zwei Gruppen aufgeteilt: Die ersten drei Befragten und die letzten sieben Befragten. Ereignis
gilt
Die 10 Befragten werden in zwei Gruppen aufgeteilt: Die ersten drei Befragten und die letzten sieben Befragten. Ereignis  gilt genau dann, wenn auf den ersten drei und auf den letzten sieben Plätzen genau ein Treffer ist.
Es handelt sich hierbei wieder um das Ziehen aus einer ungeordneten Stichprobe ohne Zurücklegen.
Es gibt somit
gilt genau dann, wenn auf den ersten drei und auf den letzten sieben Plätzen genau ein Treffer ist.
Es handelt sich hierbei wieder um das Ziehen aus einer ungeordneten Stichprobe ohne Zurücklegen.
Es gibt somit  Möglichkeiten, einen Treffer auf drei Plätze zu verteilen, sowie
Möglichkeiten, einen Treffer auf drei Plätze zu verteilen, sowie  Möglichkeiten, einen Treffer auf sieben Plätze zu verteilen.
Zusammen ergibt dies also
Möglichkeiten, einen Treffer auf sieben Plätze zu verteilen.
Zusammen ergibt dies also  Möglichkeiten für Ereignis
Möglichkeiten für Ereignis  .
3. Schritt:
.
3. Schritt:  berechnen
Durch Einsetzen der bestimmten Werte folgt:
berechnen
Durch Einsetzen der bestimmten Werte folgt:
 Die Wahrscheinlichkeit für Ereignis
Die Wahrscheinlichkeit für Ereignis  beträgt folglich etwa
beträgt folglich etwa 
2
Anteil der 25- bis 54-Jährigen, die das Internet für Telefonate nutzen
 die Anzahl von Internetnutzern im Jahr 2013. Somit sind
die Anzahl von Internetnutzern im Jahr 2013. Somit sind  Internetnutzer 24 bis 54 Jahre alt.
Damit gilt:
Der gesuchte Anteil entspricht folglich
Internetnutzer 24 bis 54 Jahre alt.
Damit gilt:
Der gesuchte Anteil entspricht folglich  Anteil der 10- bis 24-Jährigen Internetnutzer
Die Internetnutzer wurden in drei Gruppen nach ihrem Alter aufgeteilt. Der Anteil der 25- bis 54-Jährigen Nutzer von
Anteil der 10- bis 24-Jährigen Internetnutzer
Die Internetnutzer wurden in drei Gruppen nach ihrem Alter aufgeteilt. Der Anteil der 25- bis 54-Jährigen Nutzer von  ist bereits bekannt. Sei
ist bereits bekannt. Sei  der gesuchte Anteil der 10- bis 24-Jährigen Nutzern und und
der gesuchte Anteil der 10- bis 24-Jährigen Nutzern und und  der Anteil an 55-Jährigen und Älteren.
Zusammen müssen die Anteile der drei Gruppen
der Anteil an 55-Jährigen und Älteren.
Zusammen müssen die Anteile der drei Gruppen  ergeben, also ergibt sich:
ergeben, also ergibt sich:
![\(\begin{array}[t]{rll}
1&=p + 0,55 + q& \quad \mid\; -0,55 -p\\[5pt]
0,45-p&=q&
\end{array}\)](https://mathjax.schullv.de/802e34764890377d8d6309e4cc837cdb55f52624b9a6c510e4a688f7ca78682b?color=5a5a5a) Der Gesamtanteil der Internetnutzer, welche das Internet zum Telefonieren nutzen, ist gerade die Summe der mit den Altersanteilen gewichteten Einzelanteilen, das heißt:
Der Gesamtanteil der Internetnutzer, welche das Internet zum Telefonieren nutzen, ist gerade die Summe der mit den Altersanteilen gewichteten Einzelanteilen, das heißt:
 Das Gleichungssystem kann mit dem CAS gelöst werden:
Das Gleichungssystem kann mit dem CAS gelöst werden:
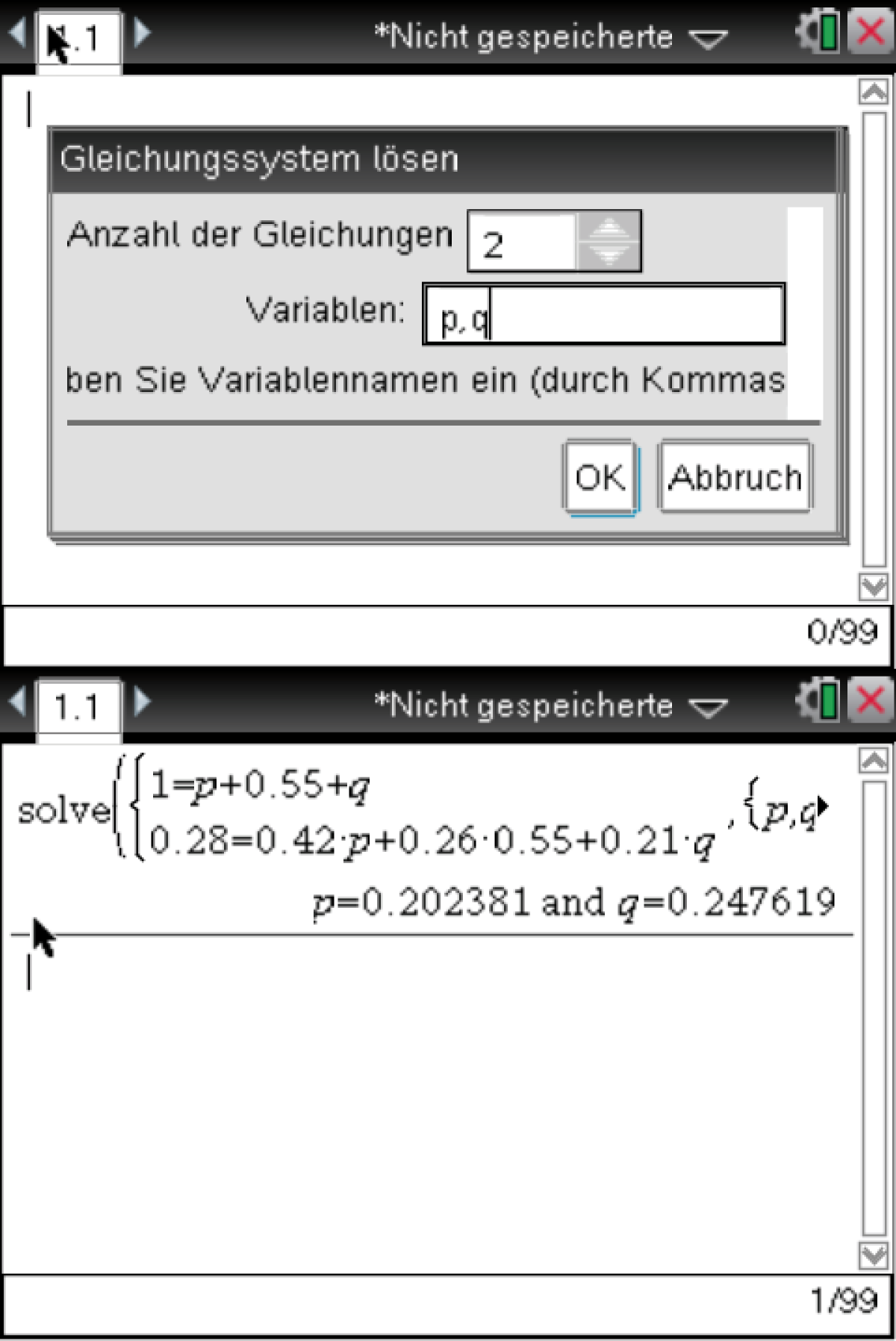 Es ergibt sich also
Es ergibt sich also  Der Anteil an Internetnutzern im Alter von 10 bis 24 Jahren beträgt somit etwa
Der Anteil an Internetnutzern im Alter von 10 bis 24 Jahren beträgt somit etwa 
aller Internetnutzer sind im Alter von 25 bis 54 Jahren
aller 24- bis 54-jähriger Internetnutzer telefonieren über das Internet
menu  3: Algebra
3: Algebra  7
7  1: Gleichungssystem lösen...
1: Gleichungssystem lösen...
Durch Eingabe der Gleichung und der zugehörigen Parameter folgt:

3
3.1
1. Schritt: Nullhypothese aufstellen
Da mit dem Hypothesentest untersucht werden soll, ob der Anteil der Internetnutzer, die über das Internet telefonieren, größer als 28 % im Jahr 2013 ist, muss die Nullhypothese hier wie folgt lauten:
 Es handelt sich folglich um einen rechtsseitigen Hypothesentest. Die Gegenhypothese
Es handelt sich folglich um einen rechtsseitigen Hypothesentest. Die Gegenhypothese  muss demnach wie folgt lauten:
muss demnach wie folgt lauten:
 2. Schritt: Entscheidungsregel formulieren
Die Zufallsvariable
2. Schritt: Entscheidungsregel formulieren
Die Zufallsvariable  beschreibt die die Anzahl an Internetnutzern unter den 50 Befragten, welche über das Internet telefonieren.
beschreibt die die Anzahl an Internetnutzern unter den 50 Befragten, welche über das Internet telefonieren.  ist binomialverteilt mit
ist binomialverteilt mit  und
und  Mit dem Signifikanzniveau
Mit dem Signifikanzniveau  können Annahme- und Ablehnungsbereich bestimmt werden:
können Annahme- und Ablehnungsbereich bestimmt werden:
![\(\begin{array}[t]{rll}
P(Z \geq k)&\leq& \alpha\\[5pt]
1- P(Z \lt k)&\leq& 0,01\\[5pt]
1-P(Z \leq k-1)&\leq& 0,01 &\quad \mid\; -1\\[5pt]
-P(Z \leq k-1)&\leq& -0,99&\quad\mid\; \cdot \left(-1\right)\\[5pt]
P(Z \leq k-1)&\geq& 0,99\\[5pt]
\end{array}\)](https://mathjax.schullv.de/45f8ae66fc7656782c1088d458ce634a5b507402d8058f62644f8443405403b2?color=5a5a5a) Mit der Tabelle für die summierte Binomialverteilung aus dem Material ergitb sich:
Mit der Tabelle für die summierte Binomialverteilung aus dem Material ergitb sich:

 Da hier also
Da hier also  gilt, folgt
gilt, folgt  .
Somit ergibt sich also:
.
Somit ergibt sich also:
 liegt.
liegt.
- Annahmebereich:
- Ablehnungsbereich:
3.2
1
1.1
Es handelt sich hierbei um eine Bernoulli-Kette mit Parametern  und
und  .
Die Zufallsvariable
.
Die Zufallsvariable  gibt an, wie viele der ersten zehn befragten Personen über das Internet telefonieren.
gibt an, wie viele der ersten zehn befragten Personen über das Internet telefonieren.  kann hier als binomialverteilt mit
kann hier als binomialverteilt mit  und
und  angenommen werden.
Wahrscheinlichkeit, dass genau drei Personen das Internet für Telefonate nutzen
Binomialverteilte Wahrscheinlichkeiten können mit dem CAS berechnet werden. Dazu muss in den Calculator-Modus gewechselt werden.
angenommen werden.
Wahrscheinlichkeit, dass genau drei Personen das Internet für Telefonate nutzen
Binomialverteilte Wahrscheinlichkeiten können mit dem CAS berechnet werden. Dazu muss in den Calculator-Modus gewechselt werden.
 ,
,  und
und  ergibt sich:
ergibt sich:
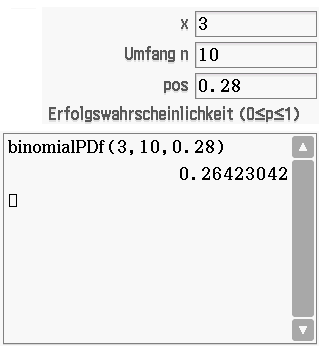 Es folgt
Es folgt  Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen genau drei Personen über das Internet telefonieren, beträgt somit etwa
Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen genau drei Personen über das Internet telefonieren, beträgt somit etwa  Wahrscheinlichkeit, dass höchstens drei Personen das Internet für Telefonate nutzen
Mit dem CAS ergibt sich analog zum ersten Ereignis:
Wahrscheinlichkeit, dass höchstens drei Personen das Internet für Telefonate nutzen
Mit dem CAS ergibt sich analog zum ersten Ereignis:
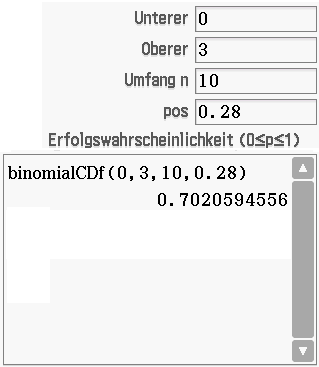 Es folgt also
Es folgt also  .
Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen höchstens drei Personen über das Internet telefonieren, beträgt somit
.
Die Wahrscheinlichkeit dafür, dass unter den ersten zehn befragten Personen höchstens drei Personen über das Internet telefonieren, beträgt somit 
Interaktiv  Verteilungsfunktionen
Verteilungsfunktionen  Diskret
Diskret  BinomialPdf
BinomialPdf
Nach Eingabe der Parameter 
Interaktiv  Verteilungsfunktionen
Verteilungsfunktionen  Diskret
Diskret  BinomialCdf
BinomialCdf

1.2
1. Schritt: Anzahl der Möglichkeiten, die Treffer und Nieten anzuordnen
Laut Aufgabenstellung nutzen zwei von zehn der befragten Personen das Internet für Telefonate. Somit gibt es in dieser Situation zwei Treffer und 8 Nieten.
Hierbei handelt es sich um das Ziehen aus einer ungeordneten Stichprobe ohne Zurücklegen.
Somit gibt es  Möglichkeiten, die Treffer und Nieten anzuordnen.
2. Schritt: Anzahl der Möglichkeiten, dass Ereignis
Möglichkeiten, die Treffer und Nieten anzuordnen.
2. Schritt: Anzahl der Möglichkeiten, dass Ereignis  gilt
Die 10 Befragten werden in zwei Gruppen aufgeteilt: Die ersten drei Befragten und die letzten sieben Befragten. Ereignis
gilt
Die 10 Befragten werden in zwei Gruppen aufgeteilt: Die ersten drei Befragten und die letzten sieben Befragten. Ereignis  gilt genau dann, wenn auf den ersten drei und auf den letzten sieben Plätzen genau ein Treffer ist.
Es handelt sich hierbei wieder um das Ziehen aus einer ungeordneten Stichprobe ohne Zurücklegen.
Es gibt somit
gilt genau dann, wenn auf den ersten drei und auf den letzten sieben Plätzen genau ein Treffer ist.
Es handelt sich hierbei wieder um das Ziehen aus einer ungeordneten Stichprobe ohne Zurücklegen.
Es gibt somit  Möglichkeiten, einen Treffer auf drei Plätze zu verteilen, sowie
Möglichkeiten, einen Treffer auf drei Plätze zu verteilen, sowie  Möglichkeiten, einen Treffer auf sieben Plätze zu verteilen.
Zusammen ergibt dies also
Möglichkeiten, einen Treffer auf sieben Plätze zu verteilen.
Zusammen ergibt dies also  Möglichkeiten für Ereignis
Möglichkeiten für Ereignis  .
3. Schritt:
.
3. Schritt:  berechnen
Durch Einsetzen der bestimmten Werte folgt:
berechnen
Durch Einsetzen der bestimmten Werte folgt:
 Die Wahrscheinlichkeit für Ereignis
Die Wahrscheinlichkeit für Ereignis  beträgt folglich etwa
beträgt folglich etwa 
2
Anteil der 25- bis 54-Jährigen, die das Internet für Telefonate nutzen
 die Anzahl von Internetnutzern im Jahr 2013. Somit sind
die Anzahl von Internetnutzern im Jahr 2013. Somit sind  Internetnutzer 24 bis 54 Jahre alt.
Damit gilt:
Der gesuchte Anteil entspricht folglich
Internetnutzer 24 bis 54 Jahre alt.
Damit gilt:
Der gesuchte Anteil entspricht folglich  Anteil der 10- bis 24-Jährigen Internetnutzer
Die Internetnutzer wurden in drei Gruppen nach ihrem Alter aufgeteilt. Der Anteil der 25- bis 54-Jährigen Nutzer von
Anteil der 10- bis 24-Jährigen Internetnutzer
Die Internetnutzer wurden in drei Gruppen nach ihrem Alter aufgeteilt. Der Anteil der 25- bis 54-Jährigen Nutzer von  ist bereits bekannt. Sei
ist bereits bekannt. Sei  der gesuchte Anteil der 10- bis 24-Jährigen Nutzern und und
der gesuchte Anteil der 10- bis 24-Jährigen Nutzern und und  der Anteil an 55-Jährigen und Älteren.
Zusammen müssen die Anteile der drei Gruppen
der Anteil an 55-Jährigen und Älteren.
Zusammen müssen die Anteile der drei Gruppen  ergeben, also ergibt sich:
ergeben, also ergibt sich:
![\(\begin{array}[t]{rll}
1&=p + 0,55 + q& \quad \mid\; -0,55 -p\\[5pt]
0,45-p&=q&
\end{array}\)](https://mathjax.schullv.de/802e34764890377d8d6309e4cc837cdb55f52624b9a6c510e4a688f7ca78682b?color=5a5a5a) Der Gesamtanteil der Internetnutzer, welche das Internet zum Telefonieren nutzen, ist gerade die Summe der mit den Altersanteilen gewichteten Einzelanteilen, das heißt:
Der Gesamtanteil der Internetnutzer, welche das Internet zum Telefonieren nutzen, ist gerade die Summe der mit den Altersanteilen gewichteten Einzelanteilen, das heißt:
 Das Gleichungssystem kann mit dem CAS gelöst werden:
Das Gleichungssystem kann mit dem CAS gelöst werden:
 Es ergibt sich also
Es ergibt sich also  Der Anteil an Internetnutzern im Alter von 10 bis 24 Jahren beträgt somit etwa
Der Anteil an Internetnutzern im Alter von 10 bis 24 Jahren beträgt somit etwa 
aller Internetnutzer sind im Alter von 25 bis 54 Jahren
aller 24- bis 54-jähriger Internetnutzer telefonieren über das Internet
Keyboard 

Durch Eingabe der Gleichung und der zugehörigen Parameter folgt:

3
3.1
1. Schritt: Nullhypothese aufstellen
Da mit dem Hypothesentest untersucht werden soll, ob der Anteil der Internetnutzer, die über das Internet telefonieren, größer als 28 % im Jahr 2013 ist, muss die Nullhypothese hier wie folgt lauten:
 Es handelt sich folglich um einen rechtsseitigen Hypothesentest. Die Gegenhypothese
Es handelt sich folglich um einen rechtsseitigen Hypothesentest. Die Gegenhypothese  muss demnach wie folgt lauten:
muss demnach wie folgt lauten:
 2. Schritt: Entscheidungsregel formulieren
Die Zufallsvariable
2. Schritt: Entscheidungsregel formulieren
Die Zufallsvariable  beschreibt die die Anzahl an Internetnutzern unter den 50 Befragten, welche über das Internet telefonieren.
beschreibt die die Anzahl an Internetnutzern unter den 50 Befragten, welche über das Internet telefonieren.  ist binomialverteilt mit
ist binomialverteilt mit  und
und  Mit dem Signifikanzniveau
Mit dem Signifikanzniveau  können Annahme- und Ablehnungsbereich bestimmt werden:
können Annahme- und Ablehnungsbereich bestimmt werden:
![\(\begin{array}[t]{rll}
P(Z \geq k)&\leq& \alpha\\[5pt]
1- P(Z \lt k)&\leq& 0,01\\[5pt]
1-P(Z \leq k-1)&\leq& 0,01 &\quad \mid\; -1\\[5pt]
-P(Z \leq k-1)&\leq& -0,99&\quad\mid\; \cdot \left(-1\right)\\[5pt]
P(Z \leq k-1)&\geq& 0,99\\[5pt]
\end{array}\)](https://mathjax.schullv.de/45f8ae66fc7656782c1088d458ce634a5b507402d8058f62644f8443405403b2?color=5a5a5a) Mit der Tabelle für die summierte Binomialverteilung aus dem Material ergitb sich:
Mit der Tabelle für die summierte Binomialverteilung aus dem Material ergitb sich:

 Da hier also
Da hier also  gilt, folgt
gilt, folgt  .
Somit ergibt sich also:
.
Somit ergibt sich also:
 liegt.
liegt.
- Annahmebereich:
- Ablehnungsbereich:
3.2