C – Lineare Algebra / Analytische Geometrie

Gegeben sind die drei Punkte $A(6\mid 3\mid 0),$ $B(2\mid 5\mid 0)$ und $D(6,5\mid 4 \mid 5).$ Eine Koordinateneinheit entspricht einem Meter.

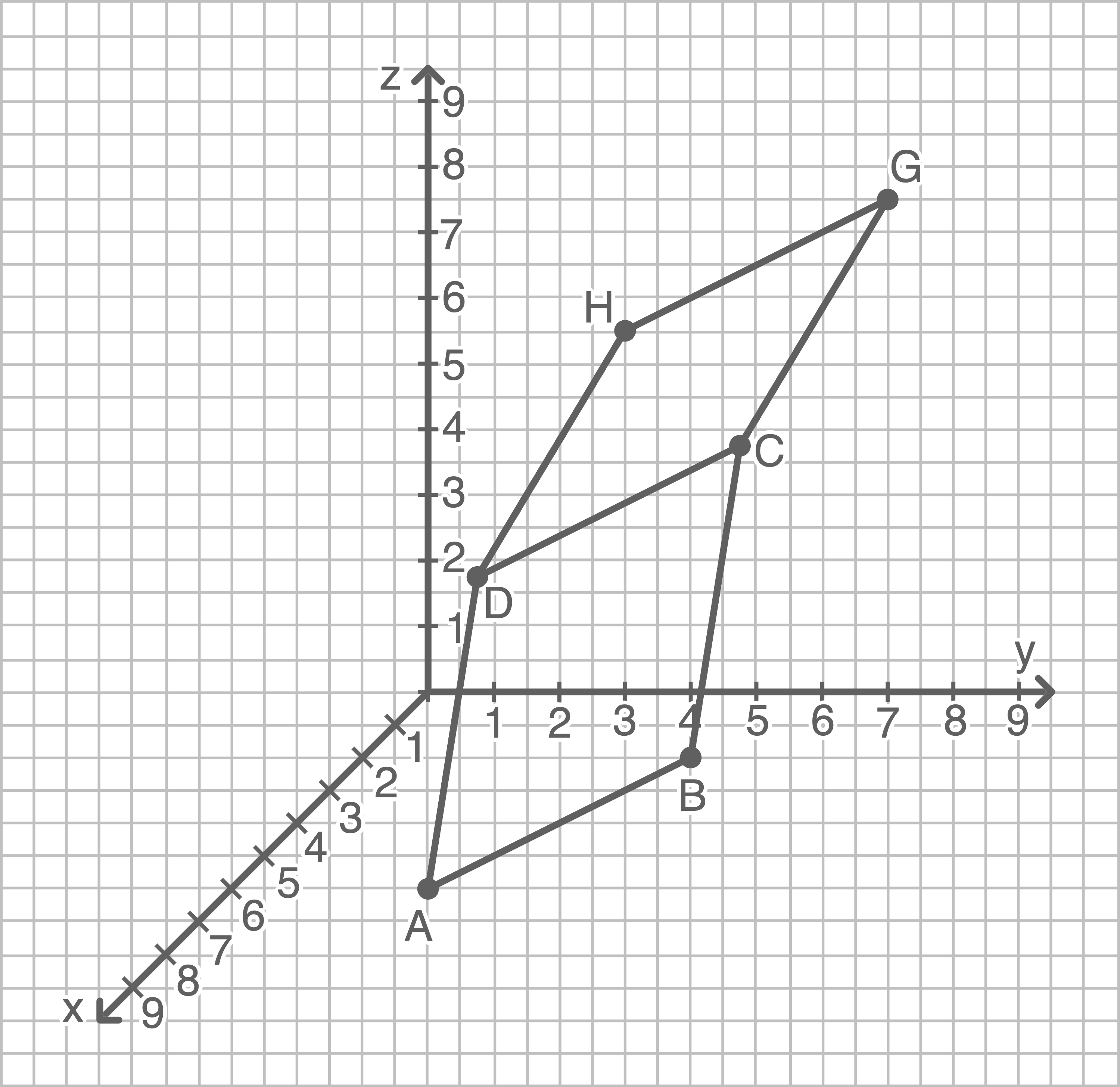
1.1

Gib eine Parametergleichung der Ebene $E_1$ an, welche die Punkte $A,B$ und $D$ enthält.

Bestimme eine zugehörige Koordinatengleichung.

$\big[$ zur Kontrolle: $E_1: 2 x+4 y-z=24 \big]$

(5 BE)

1.2

Zeige, dass der Punkt $C(2,5 \mid 6 \mid 5)$ in der Ebene $E_1$ liegt und gemeinsam mit den drei gegebenen Punkten ein Rechteck $A B C D$ bildet.

(4 BE)

In einem mathematischen Modell stellt das Rechteck $ABCD$ den unteren Teil einer Kletterwand dar.

Der obere Teil der Kletterwand besteht aus einem weiteren Rechteck, das auf die Kante $\overline{CD}$ gesetzt wird, einen Flächeninhalt von $25 \,\text{m}^2$ besitzt und nach vorne geneigt ist (Abbildung).

Der obere Teil der Kletterwand liegt in der Ebene $E_2: \; 3 x+6 y-5 z=18,5.$

Blick auf die Kletterwand von vorne

2.1

Zur Bestimmung des Eckpunktes $G$ des oberen Teils der Kletterwand wird der Ansatz im Kasten betrachtet.

Deute den Vektor $\overrightarrow{v}$ in Zeile $(1)$ geometrisch und beschreibe das Vorgehen in Zeile $(2).$

Berechne ausgehend von Zeile $(2)$ mit Hilfe des Vektors $\overrightarrow{v}$ die Koordinaten von $G$ auf eine Nachkommastelle gerundet.

Ansatz anzeigen

(6 BE)

2.2

Bestimme den Winkel zwischen dem oberen Teil der Kletterwand und der Vertikalen.

(3 BE)

Die Flugbahn einer Drohne, die für die Fernsehübertragung eines Kletterevents spektakuläre Aufnahmen an der Kletterwand erstellen soll, kann im Modell für $-1\lt \mathrm{t} \lt 1,$ $t \in \mathbb{R},$ durch die Gleichung $h: \overrightarrow{x}=\pmatrix{8\\10\\6}+t \cdot \pmatrix{1\\1\\0}+t^2 \cdot \pmatrix{2\\1\\0}$ angegeben werden.

Aus Sicherheitsgründen muss der Abstand der Drohne zur Kletterwand mindestens $4\,\text{m}$ betragen.

3.1

Begründe, dass die Drohne auf der durch $h$ beschriebenen Flugbahn ihre Höhe nicht ändert.

(2 BE)

3.2

Der Abstand eines Punktes $P$ von einer Ebene $E$ kann mit Hilfe der Formel $d=\left|(\overrightarrow{p}-\overrightarrow{a}) \cdot \overrightarrow{n_0}\right|$ ermittelt werden.

Hierbei ist $\overrightarrow{p}$ der Ortsvektor des Punktes $P,$ $\overrightarrow{a}$ der Ortsvektor eines beliebigen Punktes $A$ von $E$ und $\overrightarrow{n_0}$ ein Normalenvektor von $E$ mit der Länge 1.

Betrachtet wird folgende Herleitung:

Herleitung anzeigen

Erläutere die Ansätze in den Zeilen $(1)$ und $(2)$ im Sachzusammenhang.

Begründe unter Zuhilfenahme der Aussage in Zeile $(4),$ dass die Ungleichung für den 2. Fall in Zeile $(3)$ für alle Werte von $t$ erfüllt ist, und deute diesen Sachverhalt im Sachzusammenhang.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Parametergleichung angeben

Eine mögliche Parametergleichung, die die Punkte $A,$ $B$ und $D$ enthält, lautet:

$E_1: \quad \overrightarrow{x}= \overrightarrow{OA}+s\cdot \overrightarrow{AB}+t\cdot \overrightarrow{AD}$

Vollständige Ebenengleichung anzeigen

Koordinatengleichung bestimmen

Mit dem Kreuzprodukt zweier Richtungsvektoren der Ebene ergibt sich ein Normalenvektor $\overrightarrow{n}$ von $E_1:$

$\begin{array}[t]{rll} \overrightarrow{n}&=& \overrightarrow{AB} \times \overrightarrow{AD} & \\[5pt] &=& \pmatrix{-4\\2\\0} \times \pmatrix{0,5\\1\\5} & \\[5pt] &=& \pmatrix{2\cdot 5-0\cdot 1\\ 0\cdot 0,5-(-4)\cdot 5\\(-4)\cdot 1-2\cdot 0,5} & \\[5pt] &=& \pmatrix{10\\20\\-5} & \\[5pt] &=& 5\cdot \pmatrix{2\\4\\-1} \end{array}$

Einsetzen des gekürzten Normalenvektors sowie der Koordinaten eines Punktes, der in der Ebene liegt, liefert:

$\begin{array}[t]{rll} E_1: \quad 2x+4y-z&=& d &\quad \scriptsize \mid\; A(6\mid 3\mid 0) \\[5pt] 2\cdot 6+4\cdot 3-0&=& d \\[5pt] 24&=& d \end{array}$

Eine Koordinatengleichung der Ebene $E_1$ ist somit gegeben durch:

$E_1: \quad 2x + 4y - z = 24$

1.2

Punkt $\boldsymbol{C}$ nachweisen

Punktprobe mit den Koordinaten von $C$ ergibt:

$\begin{array}[t]{rll} 2\cdot 2,5 + 4\cdot 6- 5&=& 24 & \\[5pt] 24&=& 24 \end{array}$

Somit liegt der Punkt $C$ in der Ebene $E_1.$

Rechteck zeigen

In einem Rechteck müssen die gegenüberliegenden Seiten jeweils gleich lang sein und benachbarte Seiten orthogonal zueinander stehen.

Die Längen der Seiten ergeben sich zu:

$\begin{array}[t]{rll} |\overrightarrow{AB}|&=& \left| \pmatrix{-4 \\ 2 \\ 0} \right| & \\[5pt] &=& \sqrt{(-4)^2 + 2^2 + 0^2} & \\[5pt] &=& \sqrt{20} \end{array}$

$\begin{array}[t]{rll} |\overrightarrow{BC}|&=& \left| \pmatrix{0,5 \\ 1 \\ 5} \right| & \\[5pt] &=& \sqrt{(0,5)^2 + 1^2 + 5^2} & \\[5pt] &=& \sqrt{26,25} \end{array}$

$\begin{array}[t]{rll} |\overrightarrow{CD}|&=& \left| \pmatrix{4 \\ -2 \\ 0} \right| & \\[5pt] &=& \sqrt{(4)^2 + (-2)^2 + 0^2} & \\[5pt] &=& \sqrt{20} \end{array}$

$\begin{array}[t]{rll} |\overrightarrow{AD}|&=& \left| \pmatrix{0,5 \\ 1 \\ 5} \right| & \\[5pt] &=& \sqrt{(0,5)^2 + 1^2 + 5^2}& \\[5pt] &=& \sqrt{26,25} \end{array}$

Es gilt somit:

$|\overrightarrow{AB}| = |\overrightarrow{CD}|$ und $|\overrightarrow{AD}| = |\overrightarrow{BC}|$

Zwei Vektoren sind orthogonal zueinander, wenn ihr Skalarprodukt null ist:

$\begin{array}[t]{rll} \overrightarrow{AB} \circ \overrightarrow{AD} &=& (-4 \cdot 0,5) + (2 \cdot 1) + (0 \cdot 5)&\\[5pt] &=& -2 + 2 + 0 &\\[5pt] &=& 0 \end{array}$

$\begin{array}[t]{rll} \overrightarrow{BC} \cdot \overrightarrow{CD}&=& (0,5 \cdot 4) + (1 \cdot (-2)) + (5 \cdot 0)& \\[5pt] &=& 2 - 2 + 0& \\[5pt] &=& 0 \end{array}$

Somit sind die benachbarten Seiten jeweils orthogonal zueinander.

Der Punkt $C$ bildet mit den gegebenen Punkten somit ein Rechteck $ABCD.$

2.1

Vektor deuten

Der Vektor $\overrightarrow{v}$ in Zeile $(1)$ beschreibt das gekürzte Ergebnis des Kreuzprodukts der Vektoren $\overrightarrow{CD}$ und $\overrightarrow{n_{E_2}}$ und stellt somit einen Vektor dar, der senkrecht zu beiden Vektoren steht. Somit beschreibt der Vektor $\overrightarrow{v}$ genau den Richtungsvektor der Ebene, der die Richtung der Kante $\overline{CG}$ des rechteckigen oberen Teils der Kletterwand beschreibt.

Vorgehen beschreiben

In Zeile $(2)$ wird die Länge des Vektors $\overrightarrow{CG}$ berechnet, um den Punkt $G,$ den Eckpunkt des oberen Teils der Kletterwand, zu bestimmen.

Da der Flächeninhalt sowie die Seitenlänge $|\overrightarrow{CD}|$ bekannt ist, kann die Formel $A=|\overrightarrow{CD}|\cdot |\overrightarrow{CG}|$ nach $|\overrightarrow{CG}|$ umgestellt werden:

$\begin{array}[t]{rll} |\overrightarrow{C G}|&=& \dfrac{A}{|\overrightarrow{C D}|}& \\[5pt] &=& \dfrac{25}{2 \cdot \sqrt{5}}& \\[5pt] &=& 2,5 \cdot \sqrt{5} \; [\,\text{m}] \end{array}$

Koordinaten berechnen

Richtungsvektor $\overrightarrow{v}$ normieren:

$\begin{array}[t]{rll} \overrightarrow{v_\text{norm}}&=& \dfrac{1}{\left| \overrightarrow{v} \right|}\cdot \overrightarrow{v}& \\[5pt] &=& \dfrac{1}{\sqrt{1^2+2^2+3^2}}\pmatrix{1\\2\\3}& \\[5pt] &=& \dfrac{1}{\sqrt{14}}\pmatrix{1\\2\\3} & \\[5pt] &=& \pmatrix{0,27\\0,53\\0,80} \end{array}$

Da der normierte Richtungsvektor eine Länge von $1 \,\text{LE}$ hat und die Richtung der Strecke $\overline{CG}$ angibt, folgt:

$\begin{array}[t]{rll} \overrightarrow{OG}&=& \overrightarrow{OC}+2,5 \cdot \sqrt{5}\cdot\overrightarrow{v_\text{norm}}& \\[5pt] &=& \pmatrix{2,5\\6\\5}+2,5 \cdot \sqrt{5}\cdot \pmatrix{0,27\\0,53\\0,80} & \\[5pt] &\approx& \pmatrix{4,0\\9,0\\9,5} & \\[5pt] \end{array}$

Die auf eine Nachkommastelle gerundeten Koordinaten von $G$ ergeben sich somit zu $G(4 \mid 9\mid 9,5).$

2.2

Ein Normalenvektor der Ebene $E_2$ ist gegeben durch $\overrightarrow{n_{E_2}}=\pmatrix{3\\6\\-5}.$

Ein Richtungsvektor der Vertikalen ist beispielsweise $\overrightarrow{r_V} = \pmatrix{0 \\ 0 \\ 1}.$

Für den gesuchten Winkel gilt:

Rechnung anzeigen

$\alpha \approx 36,7 ^\circ$

Der Winkel zwischen dem oberen Teil der Kletterwand und der Vertikalen beträgt somit $36,7^\circ.$

3.1

Die Höhe der Flugbahn wird durch die $z$ -Koordinate der Parametergleichung beschrieben.

Für diese gilt:

$z_h=6+t\cdot 0+t^2\cdot 0=6$

Somit ist die Höhe unabhängig vom Parameter $t$ und ändert sich folglich nicht.

3.2

Zeile $\boldsymbol{(1)}$ erläutern

In Zeile $(1)$ wird der senkrechte Abstand $d(t)$ eines Punktes $P,$ der auf der Flugbahn $h$ liegt, von der Ebene $E_2,$ die den oberen Teil der Kletterwand beschreibt, berechnet.

Für den Vektor $\overrightarrow{p}$ wird hierfür der Ortsvektor eines allgemeinen Punktes auf $h$ und für $\overrightarrow{a}$ der Ortsvektor $\overrightarrow{OD}$ eines Punktes der Ebene $E_2$ eingesetzt.

Durch den Faktor $\dfrac{1}{\sqrt{70}}$ wird der Normalenvektor der Ebene $E_2$ normiert, sodass seine Länge genau 1 beträgt.

Zeile $\boldsymbol{(2)}$ erläutern

In Zeile (2) wird die Bedingung für den minimalen Abstand aus der Aufgabenstellung aufgestellt.

Es wird gefordert, dass der Abstand $d(t)$ mindestens 4 Meter betragen muss, sodass die Drohne auf ihrer Flugbahn stets mindestens 4 Meter von der Kletterwand entfernt bleibt.

Ungleichung begründen

Da der quadratische Term $12t^2$ positiv ist, hat die Funktion $d(t)$ die Form einer nach oben geöffneten Parabel und laut der Aussage in Zeile $(4)$ keinen Schnittpunkt mit der Geraden $d(t)=4.$ Folglich muss sie vollständig oberhalb der Geraden $d(t)=4$ verlaufen und es gilt $d(t)\gt 4$ für alle Werte von $t.$

Die Ungleichung für den 2. Fall ist somit für alle Werte von $t$ erfüllt.

Sachverhalt deuten

Die Bedingung, dass der Abstand zur Kletterwand mindestens 4 Meter betragen muss, wird jederzeit eingehalten. Die Drohne kommt während ihres gesamten Fluges nie zu nah an die Kletterwand heran.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?