D – Stochastik

Ein bekannter Video-Streamingdienst bietet einen kostenpflichtigen Zugang zu Spielfilmen und Serien an.

Personen, die davon gegen Zahlung einer monatlichen Gebühr Gebrauch machen, werden im Folgenden als Abonnenten bezeichnet. Sie haben sich entweder für das Spielfilmpaket oder für das Komplettpaket entschieden, das neben den Spielfilmen auch noch Serien enthält.

Unter den Abonnenten sind $70 \,\%$ höchstens 40 Jahre alt. Von diesen haben $80 \,\%$ das Komplettpaket gewählt. Bei den über 40-jährigen Abonnenten haben sich $50 \,\%$ für das Komplettpaket entschieden.

1.1

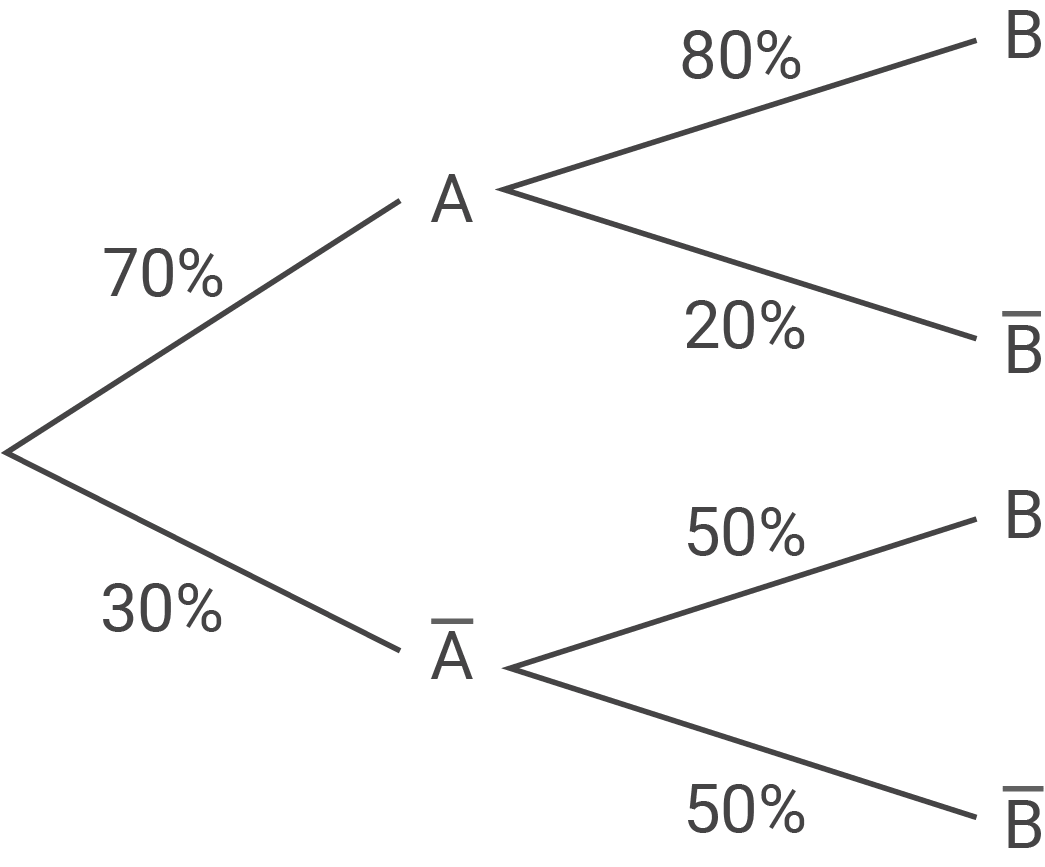
Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 BE)

1.2

Eine unter allen Abonnenten zufällig ausgewählte Person hat sich für das Komplettpaket entschieden.

Bestimme die Wahrscheinlichkeit dafür, dass sie höchstens 40 Jahre alt ist.

(3 BE)

1.3

Bestimme die Anzahl der Abonnenten, die man mindestens zufällig auswählen müsste, damit unter ihnen mit einer Wahrscheinlichkeit von mindestens $99 \;\%$ mehr als 20 Personen älter als 40 Jahre sind.

(4 BE)

Der Anteil der zufriedenen Abonnenten von derzeit $60 \;\%$ soll gesteigert werden. Dazu wird ein Algorithmus entwickelt, der jedem Abonnenten täglich individuell einen Spielfilm vorschlägt. Als Basis für die Entscheidung über den dauerhaften Einsatz des Algorithmus plant das Management einen Probebetrieb.

Im Anschluss soll die Nullhypothese „Der Anteil der zufriedenen Abonnenten beträgt höchstens $60 \;\%.$ “ mit Hilfe einer Stichprobe von 200 zufällig ausgewählten Abonnenten auf einem Signifikanzniveau von $5 \;\%$ getestet werden.

2.1

Gib an, welche Überlegung des Managements zur Wahl dieser Nulllhypothese geführt haben könnte.

(2 BE)

2.2

Für den beschriebenen Test ergibt sich $\{132 ; 133 ; \ldots ; 200\}$ als der Ablehnungsbereich der Nullhypothese.

2.2.1

Zur Bestimmung der unteren Grenze dieses Ablehnungsbereichs wurden zunächst folgende Lösungsschritte ausgeführt:

$Y:$ Anzahl der zufriedenen Abonnenten in der Stichprobe

$P_{0,6}^{200}(Y \geq 132)=1-F_{200;0,6}(131)$ $\approx 0,047$

Begründe, dass die beiden Lösungsschritte zur Bestimmung der unteren Grenze nicht ausreichend sind, und gib die fehlenden Lösungsschritte an.

(4 BE)

2.2.2

Weise nach, dass die Wahrscheinlichkeit für einen Fehler zweiter Art bei diesem Ablehnungsbereich der Nullhypothese mehr als $90 \;\%$ betragen könnte.

(4 BE)

Zur Anmeldung auf der Webseite des Streamingdiensts ist ein persönliches Kennwort erforderlich. Für das Kennwort können 80 verschiedene Zeichen verwendet werden: je 26 Groß- und Kleinbuchstaben, 10 Ziffern sowie 18 Sonderzeichen.

3.1

Einige Abonnenten verwenden ein Kennwort, das genau acht Zeichen lang ist und nur aus Kleinbuchstaben besteht. Dabei können Zeichen mehrfach vorkommen.

Zeige, dass für diese Abonnenten weniger als ein Tausendstel aller möglichen Kennwörter infrage kommen, die aus genau acht Zeichen bestehen.

(2 BE)

3.2

Niclas beschließt ein Kennwort zu wählen, das die beiden folgenden Bedingungen erfüllt:

Es besteht aus genau acht Zeichen, die untereinander verschieden sind.
Die Buchstaben seines Namens sind in der korrekten Reihenfolge und unter Berücksichtigung der Groß- und Kleinschreibung enthalten.

Damit sind beispielsweise Nic4+las oder nNicl*as mögliche Kennwörter.

Bestimme die Anzahl aller derartigen Kennwörter.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$A:$

„Ein Abonnent ist höchstens 40 Jahre alt.“

$B:$

„Ein Abonnent hat das Komplettpaket.“

Baumdiagramm Videostreaming Komplettpaket Mathe Abi 2024

1.2

$\begin{array}[t]{rll} P_B(A)&=&\dfrac{P(A\cap B)}{P(B)} \\[5pt] &=&\dfrac{0,7\cdot0,8}{0,7\cdot0,8+0,3\cdot0,5} \\[5pt] &=&\dfrac{0,56}{0,71} \\[5pt] &\approx&0,79 \\[5pt] &=& 79 \,\% \end{array}$

1.3

Die Zufallsvariable $Z$ gibt die Anzahl der Abonnenten an, die älter als 40 Jahre sind und ist binomialverteilt mit unbekanntem $n$ und $p=0,3.$ Es ist nun der minimale Wert von $n$ gesucht, sodass folgende Ungleichung erfüllt ist:

$P_{0,3}^n(Z\gt20) \geq 99\,\%$

Systematisches Ausprobieren mit dem Taschenrechner liefert:

$\begin{array}[t]{rll} P_{0,3}^{103}(Z\gt20)&=&1-P_{0,3}^{103}(Z\leq20) \\[5pt] &\approx&0,9896 \\[5pt] &=&98,96\,\% \end{array}$

$\begin{array}[t]{rll} P_{0,3}^{104}(Z\gt20)&=&1-P_{0,3}^{104}(Z\leq20) \\[5pt] &\approx&0,991 \\[5pt] &=&99,1\,\% \end{array}$

Es müssen somit mindestens $104$ Abonnenten zufällig ausgewählt werden, damit unter ihnen mit einer Wahrscheinlichkeit von mindestens $99\,\%$ mehr als 20 Personen älter als 40 Jahre sind.

2.1

Das Management möchte vermeiden, dass der Algorithmus dauerhaft eingesetzt wird, obwohl der Einsatz des Algorithmus die Zufriedenheit unter den Abonnenten in Wirklichkeit nicht erhöht.

2.2.1

Die beiden angegebenen Lösungsschritte sind nicht ausreichend, da zusätzlich überprüft werden muss, ob es keinen Wert $k$ gibt, der kleiner als 132 ist und für den $P_{0,6}^{200}(Y \geq k) \leq 0,05$ gilt. Mit dem Taschenrechner folgt für $k=131:$

$\begin{array}[t]{rll} P_{0,6}^{200}(Y \geq 131)&=& 1-P_{0,6}^{200}(Y \leq 130) \\[5pt] &\approx&0,064 \end{array}$

Als eine geeignete Ergänzung der angegebenen Lösungsschritte ergibt sich somit:

$Y:\;$ Anzahl der zufriedenen Abonnenten in der Stichprobe
$P_{0,6}^{200}(Y \geq 132) \approx 0,047$
$P_{0,6}^{200}(Y \geq 131) \approx 0,064$

2.2.2

Der Fehler zweiter Art tritt auf, wenn die Nullhypothese nicht abgelehnt wird, obwohl sie in Wirklichkeit falsch ist.

Bei einem Anteil von beispielsweise $61\,\%$ zufriedenen Abonnenten folgt für die Wahrscheinlichkeit des Fehlers zweiter Art:

$\begin{array}[t]{rll} P_{0,61}^{200}(Y \leq 131)&\approx& 0,917 \\[5pt] &=& 91,7\,\% \end{array}$

3.1

Es gibt $80^8$ mögliche Kennwörter mit 80 verschiedenen Zeichen. Werden ausschließlich Kleinbuchstaben verwendet, stehen 26 Zeichen zur Verfügung und somit ergeben sich genau $26^8$ mögliche Kennwörter.

Es gilt also:

$\dfrac{26^8}{80^8} \approx 0,00012\lt 0,001$

3.2

Da der Name Niclas aus sechs unterschiedlichen Buchstaben besteht, bleiben für die restlichen zwei Stellen des Passworts 74 mögliche Zeichen übrig. Diese Zeichen können an zwei beliebige Stellen des Kennworts gesetzt werden.

Die Anzahl aller Möglichkeiten ergibt sich also zu:

$\pmatrix{8\\2} \cdot 74 \cdot 73=151256$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?