A1 - Analysis
Das Wachstum einer Bakterienkultur soll mit Hilfe geeigneter mathematischer Funktionen beschrieben werden.
 und
und 
Solltest du die Funktionen und
und  nicht bestimmt haben, verwende
für
nicht bestimmt haben, verwende
für  die Ersatzfunktion
die Ersatzfunktion  mit
mit  und
und
für die Ersatzfunktion
die Ersatzfunktion  mit
mit  .
.
1.
Bestimme die Funktionsgleichung einer Wachstumsfunktion  mit
mit  , deren Graph durch die Punkte
, deren Graph durch die Punkte  und
und  verläuft.
verläuft.
(4 BE)
2.
Biologen haben über einen Zeitraum von  Stunden das Wachstum einer Bakterienkultur untersucht, welche der Wirkung eines Toxins ausgesetzt wurde. Die gemessenen Ergebnisse sind in den ersten beiden Zeilen der Tabelle im Material protokolliert (
Stunden das Wachstum einer Bakterienkultur untersucht, welche der Wirkung eines Toxins ausgesetzt wurde. Die gemessenen Ergebnisse sind in den ersten beiden Zeilen der Tabelle im Material protokolliert ( entspricht der Zeit in Stunden,
entspricht der Zeit in Stunden,  der Anzahl der noch lebenden Bakterien in Tausend).
der Anzahl der noch lebenden Bakterien in Tausend).
Der Wachstumsvorgang soll durch zwei unterschiedliche Funktionen modelliert werden: Modell 1: Modell 2:
Modell 2: 
Der Wachstumsvorgang soll durch zwei unterschiedliche Funktionen modelliert werden: Modell 1:
2.1
Bestimme für jedes der beiden Modelle die zugehörige Funktionsgleichung. Verwende dazu ein geeignetes Regressionsverfahren unter Benutzung jeweils einer der beiden unteren Zeilen der im Material angegebenen Tabelle. Erkläre deine Vorgehensweise.
Verwende im Folgenden die in Aufgabe 2.1 bestimmten Funktionen
(8 BE)
Solltest du die Funktionen
für
2.2
Der Term  beschreibt ein Maß für die Abweichung einer Funktion
beschreibt ein Maß für die Abweichung einer Funktion  von gegebenen Wertepaaren
von gegebenen Wertepaaren  ,
,  . Erläutere den Aufbau des Terms.
. Erläutere den Aufbau des Terms.
Der Wert des Abweichungsmaßes für beträgt ungefähr
beträgt ungefähr  . Bestimme für die Funktion
. Bestimme für die Funktion  den Wert des Abweichungsmaßes und beurteile für beide Funktionen die Qualität der Anpassung.
den Wert des Abweichungsmaßes und beurteile für beide Funktionen die Qualität der Anpassung.
Der Wert des Abweichungsmaßes für
(6 BE)
2.3
Bestimme in beiden Modellen den jeweiligen Zeitpunkt des maximalen Bestandszuwachses der noch lebenden Bakterien sowie den jeweiligen Zeitpunkt des maximalen Bestandes. Gib jeweils die größte Anzahl der noch lebenden Bakterien an.
(6 BE)
2.4
Erläutere die Bedeutung des Schnittpunktes des Graphen  bzw.
bzw.  mit der
mit der  -Achse im Sachzusammenhang und bestimme jeweils mithilfe von
-Achse im Sachzusammenhang und bestimme jeweils mithilfe von  bzw.
bzw.  den Zeitpunkt, an dem erstmalig nach Beginn der Messung die Anzahl der noch lebenden Bakterien
den Zeitpunkt, an dem erstmalig nach Beginn der Messung die Anzahl der noch lebenden Bakterien  des Wertes von
des Wertes von  bzw.
bzw.  beträgt.
beträgt.
(5 BE)
2.5
Bestimme den Wert des Terms  und deute das Ergebnis im Sachzusammenhang.
und deute das Ergebnis im Sachzusammenhang.
(5 BE)
3.
Die Biologen vermuten, dass die Wachstumsrate  mit
mit  linear verläuft.
linear verläuft.
Berechne die Wachstumsraten und
und  für die allgemeinen Modellfunktionen
für die allgemeinen Modellfunktionen  und
und  und prüfe jeweils, ob die Vermutung der Biologen zutrifft.
und prüfe jeweils, ob die Vermutung der Biologen zutrifft.
Material
Berechne die Wachstumsraten
(6 BE)
| Zeit (in Stunden) |
Anzahl der noch lebenden Bakterien |
1/ |
|
|---|---|---|---|
1.
Funktionsgleichung bestimmen
Einsetzen von  in
in  liefert für
liefert für  Durch Einsetzen von
Durch Einsetzen von  folgt weiter:
Die Funktion für das Wachstum lautet damit
folgt weiter:
Die Funktion für das Wachstum lautet damit  .
.
2.1
Funktionsgleichung für Modell 1 bestimmen
 Unter CALC
Unter CALC  Regressionen
Regressionen  Quadratische Reg. werden nun die Parameter für die Ersatzfunktion bestimmt. Es ergibt sich
Quadratische Reg. werden nun die Parameter für die Ersatzfunktion bestimmt. Es ergibt sich  ,
,  und
und  Für die Ersatzfunktion folgt:
Für die Ersatzfunktion folgt:




 Die Funktion
Die Funktion  ergibt sich somit wie folgt:
ergibt sich somit wie folgt:

 Funktionsgleichung für Modell 2 bestimmen
Mit Hilfe einer quadratischen Regression im CAS unter Zuhilfenahme der Werte von
Funktionsgleichung für Modell 2 bestimmen
Mit Hilfe einer quadratischen Regression im CAS unter Zuhilfenahme der Werte von  und
und  ergeben sich die Parameter der Ersatzfunktion
ergeben sich die Parameter der Ersatzfunktion 
 als
als 
 und
und  Damit folgt für
Damit folgt für 


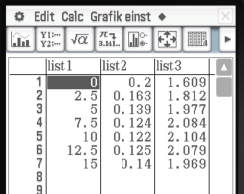
Für die Durchführung einer quadratischen Regression mit Hilfe den Werten aus der dritten Zeile der Tabelle wird zunächst eine Liste der Werte für  und
und  unter MENU
unter MENU  Statistik angelegt:
Statistik angelegt:

2.2
Termaufbau beschreiben
Der Ausdruck berechnet zunächst die Differenz zwischen den Funktionswerten  und den gegebenen Werten
und den gegebenen Werten  Diese Differenz wird quadriert und über alle
Diese Differenz wird quadriert und über alle  von
von  bis
bis  aufsummiert. Die Wurzel dieser Summe wird nun durch
aufsummiert. Die Wurzel dieser Summe wird nun durch  geteilt, was die durchschnittliche Differenz zwischen
geteilt, was die durchschnittliche Differenz zwischen  und
und  ergibt.
Wert der Abweichung berechnen
Einsetzen verschiedener Werte für
ergibt.
Wert der Abweichung berechnen
Einsetzen verschiedener Werte für  in die Funktionsgleichung von
in die Funktionsgleichung von  mit Hilfe des CAS und Betrachtung der dazugehörigen Werte
mit Hilfe des CAS und Betrachtung der dazugehörigen Werte  in der Tabelle aus dem Material liefert folgende Werte:
in der Tabelle aus dem Material liefert folgende Werte:
Durch Einsetzen dieser Werte in die oben beschriebene Formel folgt für die Abweichung von  Die Werte der Abweichung sind für beide Funktionen fast gleich und relativ klein, somit stellen beide Funktionen eine gute Annäherung der echten Werte dar.
Die Werte der Abweichung sind für beide Funktionen fast gleich und relativ klein, somit stellen beide Funktionen eine gute Annäherung der echten Werte dar.
| Zeit |
||
|---|---|---|
2.3
Maximalstellen für Modell 1 bestimmen
Zunächst wird die Funktion im CAS definiert. Mit Hilfe des "fMax"-Befehl des CAS werden dann die Maximalstelle der Funktion und Ableitung berechnet. Folgender Befehl liefert die Ableitung von 
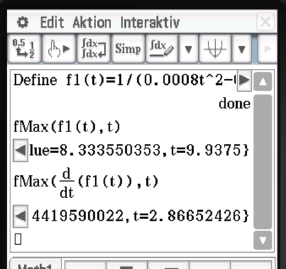 Maximalstellen für Modell 2 bestimmen
Analoges Vorgehen wie bei
Maximalstellen für Modell 2 bestimmen
Analoges Vorgehen wie bei  liefert hier, dass die Maxima bei
liefert hier, dass die Maxima bei  und
und  liegen. Die maximale Anzahl der lebenden Bakterien beträgt hier also nach
liegen. Die maximale Anzahl der lebenden Bakterien beträgt hier also nach  Stunden
Stunden 
Keyboard  Math2
Math2  Ableitung
Für die Maximalstelle von
Ableitung
Für die Maximalstelle von  folgt:
folgt:
 Da
Da 
 gilt, erreicht die Bakterienkultur nach
gilt, erreicht die Bakterienkultur nach  Stunden mit
Stunden mit  lebenden Bakterien die größte Population. Die Maximalstelle der Ableitung liegt bei
lebenden Bakterien die größte Population. Die Maximalstelle der Ableitung liegt bei  das heißt nach
das heißt nach  Stunden ist das Wachstum der Bakterienpopulation am größten.
Stunden ist das Wachstum der Bakterienpopulation am größten.

2.4
Erläutern im Sachzusammenhang
Der Schnittpunkt des Graphen von  mit der
mit der  -Achse gibt die Anzahl Bakterien zu Beginn des Beobachtungszeitraums an.
Zeitpunkt für Modell 1 bestimmen
Der CAS liefert zunächst
-Achse gibt die Anzahl Bakterien zu Beginn des Beobachtungszeitraums an.
Zeitpunkt für Modell 1 bestimmen
Der CAS liefert zunächst 
 Aufstellen von
Aufstellen von  liefert mit Hilfe des solve-Befehls des CAS:
liefert mit Hilfe des solve-Befehls des CAS:

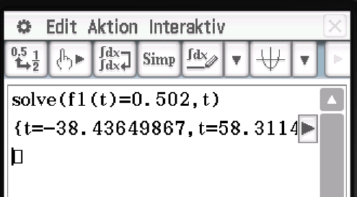 Somit beträgt die Anzahl der Bakterien nach
Somit beträgt die Anzahl der Bakterien nach  Stunden
Stunden  des Anfangswertes.
Zeitpunkt für Modell 2 bestimmen
Analoge Vorgehensweise liefert hier mit
des Anfangswertes.
Zeitpunkt für Modell 2 bestimmen
Analoge Vorgehensweise liefert hier mit 
 den Wert
den Wert  für
für  Somit sind bei der zweiten Funktion nach
Somit sind bei der zweiten Funktion nach  Stunden
Stunden  der Anfangspopulation erreicht.
der Anfangspopulation erreicht.

2.5
Integralwert bestimmen
Unter Keyboard  Math2
Math2  Integral kann das folgende Integral im CAS berechnet werden:
Integral kann das folgende Integral im CAS berechnet werden:



 Im Sachzusammenhang deuten
Das Integral gibt die Differenz der beiden Funktionen zwischen
Im Sachzusammenhang deuten
Das Integral gibt die Differenz der beiden Funktionen zwischen  und
und  an. Da durch
an. Da durch  geteilt wird, berechnet der Term die durchschnittliche Differenz im angegebenen Zeitraum. Die erste Funktion gibt somit im Zeitraum zwischen sieben und zwölf Stunden somit durchschnittlich
geteilt wird, berechnet der Term die durchschnittliche Differenz im angegebenen Zeitraum. Die erste Funktion gibt somit im Zeitraum zwischen sieben und zwölf Stunden somit durchschnittlich  Bakterien mehr an als
Bakterien mehr an als 
3.
Wachstumsrate für Modell 1 berechnen
Mit Hilfe der Kettenregel folgt für die Ableitung von 





 Für
Für  folgt dann:
folgt dann:




 Da die Potenz von
Da die Potenz von  im Nenner von
im Nenner von  größer als die im Zähler ist, kann es sich hier nicht um eine lineare Funktion handeln. Die Biologen haben damit in diesem Fall Unrecht.
Wachstumsrate für Modell 2 berechnen
Für die Ableitung der Funktion
größer als die im Zähler ist, kann es sich hier nicht um eine lineare Funktion handeln. Die Biologen haben damit in diesem Fall Unrecht.
Wachstumsrate für Modell 2 berechnen
Für die Ableitung der Funktion  folgt mit der Kettenregel:
folgt mit der Kettenregel:


 Für
Für  folgt dann:
folgt dann:


 Das ist eine lineare Funktion, die Behauptung ist somit für
Das ist eine lineare Funktion, die Behauptung ist somit für  korrekt.
korrekt.
1.
Funktionsgleichung bestimmen
Einsetzen von  in
in  liefert für
liefert für  Durch Einsetzen von
Durch Einsetzen von  folgt weiter:
Die Funktion für das Wachstum lautet damit
folgt weiter:
Die Funktion für das Wachstum lautet damit  .
.
2.1
Funktionsgleichung für Modell 1 bestimmen
 Unter CALC
Unter CALC  Regressionen
Regressionen  Quadratische Reg. werden nun die Parameter für die Ersatzfunktion bestimmt. Es ergibt sich
Quadratische Reg. werden nun die Parameter für die Ersatzfunktion bestimmt. Es ergibt sich  ,
,  und
und  Für die Ersatzfunktion folgt:
Für die Ersatzfunktion folgt:




 Die Funktion
Die Funktion  ergibt sich somit wie folgt:
ergibt sich somit wie folgt:

 Funktionsgleichung für Modell 2 bestimmen
Mit Hilfe einer quadratischen Regression im CAS unter Zuhilfenahme der Werte von
Funktionsgleichung für Modell 2 bestimmen
Mit Hilfe einer quadratischen Regression im CAS unter Zuhilfenahme der Werte von  und
und  ergeben sich die Parameter der Ersatzfunktion
ergeben sich die Parameter der Ersatzfunktion 
 als
als 
 und
und  Damit folgt für
Damit folgt für 


Für die Durchführung einer quadratischen Regression mit Hilfe den Werten aus der dritten Zeile der Tabelle wird zunächst eine Liste der Werte für  und
und  unter MENU
unter MENU  Statistik angelegt:
Statistik angelegt:

2.2
Termaufbau beschreiben
Der Ausdruck berechnet zunächst die Differenz zwischen den Funktionswerten  und den gegebenen Werten
und den gegebenen Werten  Diese Differenz wird quadriert und über alle
Diese Differenz wird quadriert und über alle  von
von  bis
bis  aufsummiert. Die Wurzel dieser Summe wird nun durch
aufsummiert. Die Wurzel dieser Summe wird nun durch  geteilt, was die durchschnittliche Differenz zwischen
geteilt, was die durchschnittliche Differenz zwischen  und
und  ergibt.
Wert der Abweichung berechnen
Einsetzen verschiedener Werte für
ergibt.
Wert der Abweichung berechnen
Einsetzen verschiedener Werte für  in die Funktionsgleichung von
in die Funktionsgleichung von  mit Hilfe des CAS und Betrachtung der dazugehörigen Werte
mit Hilfe des CAS und Betrachtung der dazugehörigen Werte  in der Tabelle aus dem Material liefert folgende Werte:
in der Tabelle aus dem Material liefert folgende Werte:
Durch Einsetzen dieser Werte in die oben beschriebene Formel folgt für die Abweichung von  Die Werte der Abweichung sind für beide Funktionen fast gleich und relativ klein, somit stellen beide Funktionen eine gute Annäherung der echten Werte dar.
Die Werte der Abweichung sind für beide Funktionen fast gleich und relativ klein, somit stellen beide Funktionen eine gute Annäherung der echten Werte dar.
| Zeit |
||
|---|---|---|
2.3
Maximalstellen für Modell 1 bestimmen
Zunächst wird die Funktion im CAS definiert. Mit Hilfe des "fMax"-Befehl des CAS werden dann die Maximalstelle der Funktion und Ableitung berechnet. Folgender Befehl liefert die Ableitung von 
 Maximalstellen für Modell 2 bestimmen
Analoges Vorgehen wie bei
Maximalstellen für Modell 2 bestimmen
Analoges Vorgehen wie bei  liefert hier, dass die Maxima bei
liefert hier, dass die Maxima bei  und
und  liegen. Die maximale Anzahl der lebenden Bakterien beträgt hier also nach
liegen. Die maximale Anzahl der lebenden Bakterien beträgt hier also nach  Stunden
Stunden 
Keyboard  Math2
Math2  Ableitung
Für die Maximalstelle von
Ableitung
Für die Maximalstelle von  folgt:
folgt:
 Da
Da 
 gilt, erreicht die Bakterienkultur nach
gilt, erreicht die Bakterienkultur nach  Stunden mit
Stunden mit  lebenden Bakterien die größte Population. Die Maximalstelle der Ableitung liegt bei
lebenden Bakterien die größte Population. Die Maximalstelle der Ableitung liegt bei  das heißt nach
das heißt nach  Stunden ist das Wachstum der Bakterienpopulation am größten.
Stunden ist das Wachstum der Bakterienpopulation am größten.

2.4
Erläutern im Sachzusammenhang
Der Schnittpunkt des Graphen von  mit der
mit der  -Achse gibt die Anzahl Bakterien zu Beginn des Beobachtungszeitraums an.
Zeitpunkt für Modell 1 bestimmen
Der CAS liefert zunächst
-Achse gibt die Anzahl Bakterien zu Beginn des Beobachtungszeitraums an.
Zeitpunkt für Modell 1 bestimmen
Der CAS liefert zunächst 
 Aufstellen von
Aufstellen von  liefert mit Hilfe des solve-Befehls des CAS:
liefert mit Hilfe des solve-Befehls des CAS:

 Somit beträgt die Anzahl der Bakterien nach
Somit beträgt die Anzahl der Bakterien nach  Stunden
Stunden  des Anfangswertes.
Zeitpunkt für Modell 2 bestimmen
Analoge Vorgehensweise liefert hier mit
des Anfangswertes.
Zeitpunkt für Modell 2 bestimmen
Analoge Vorgehensweise liefert hier mit 
 den Wert
den Wert  für
für  Somit sind bei der zweiten Funktion nach
Somit sind bei der zweiten Funktion nach  Stunden
Stunden  der Anfangspopulation erreicht.
der Anfangspopulation erreicht.

2.5
Integralwert bestimmen
Unter Keyboard  Math2
Math2  Integral kann das folgende Integral im CAS berechnet werden:
Integral kann das folgende Integral im CAS berechnet werden:



 Im Sachzusammenhang deuten
Das Integral gibt die Differenz der beiden Funktionen zwischen
Im Sachzusammenhang deuten
Das Integral gibt die Differenz der beiden Funktionen zwischen  und
und  an. Da durch
an. Da durch  geteilt wird, berechnet der Term die durchschnittliche Differenz im angegebenen Zeitraum. Die erste Funktion gibt somit im Zeitraum zwischen sieben und zwölf Stunden somit durchschnittlich
geteilt wird, berechnet der Term die durchschnittliche Differenz im angegebenen Zeitraum. Die erste Funktion gibt somit im Zeitraum zwischen sieben und zwölf Stunden somit durchschnittlich  Bakterien mehr an als
Bakterien mehr an als 
3.
Wachstumsrate für Modell 1 berechnen
Mit Hilfe der Kettenregel folgt für die Ableitung von 





 Für
Für  folgt dann:
folgt dann:




 Da die Potenz von
Da die Potenz von  im Nenner von
im Nenner von  größer als die im Zähler ist, kann es sich hier nicht um eine lineare Funktion handeln. Die Biologen haben damit in diesem Fall Unrecht.
Wachstumsrate für Modell 2 berechnen
Für die Ableitung der Funktion
größer als die im Zähler ist, kann es sich hier nicht um eine lineare Funktion handeln. Die Biologen haben damit in diesem Fall Unrecht.
Wachstumsrate für Modell 2 berechnen
Für die Ableitung der Funktion  folgt mit der Kettenregel:
folgt mit der Kettenregel:


 Für
Für  folgt dann:
folgt dann:


 Das ist eine lineare Funktion, die Behauptung ist somit für
Das ist eine lineare Funktion, die Behauptung ist somit für  korrekt.
korrekt.