C2 - Stochastik

Auf einem Flughafen werden die aufgegebenen Gepäckstücke unabängig voneinander auf ein Förderband gelegt. Die Wahrscheinlichkeit, dass ein Gepäckstück das Ziel Frankfurt hat, sei $p.$

1.1

Die Wahrscheinlichkeit, dass von zwei aufeinanderfolgenden Gepäckstücken mindestens eines nicht das Ziel Frankfurt hat, sei $93,75\,\%$ .

Berechne daraus die Wahrscheinlichkeit $p.$

$[$ zur Kontrolle: $p=0,25]$

(5 BE)

1.2

Nun werden 10 aufeinanderfolgende Gepäckstücke betrachtet.

Berechne die Wahrscheinlichkeit dafür, dass genau drei Gepäckstücke Frankfurt als Ziel haben.

(3 BE)

1.3

Von 10 aufeinanderfolgenden Gepäckstücken hat keines Frankfurt als Ziel.

Entscheide begründet, ob $P_1$ oder $P_2$ die Wahrscheinlichkeit für dieses Ereignis darstellt:

$P_{1}=(1-p)^{10}$ oder $P_{2}=1-p^{10}$

Beschreibe das Ereignis, das zu der anderen Wahrscheinlichkeit gehört.

(4 BE)

Das Handgepäck wird wie folgt kontrolliert:

Bei Kontrolle 1 wird das Gepäck mit einem Spezialgerät durchleuchtet. Nur wenn dieser Vorgang kein eindeutiges Ergebnis liefert, wird er ein zweites Mal durchgeführt (Kontrolle 2). Liegt dann immer noch kein eindeutiges Ergebnis vor, wird das Gepäckstück geöffnet und geprüft (Kontrolle 3).

Kontrolle 1 und Kontrolle 2 dauern je 10 Sekunden, Kontrolle 3 dauert 5 Minuten. Zwischen zwei Kontrollvorgängen vergehen 30 Sekunden.

Kontrolle 1 führt mit $90\,\%$ iger Wahrscheinlichkeit zu einem eindeutigen Ereignis, Kontrolle 2 nur mit $60\,\%.$

2.1

Stelle den Sachverhalt ohne Berücksichtigung der Zeiten in einem Baumdiagramm dar.

(5 BE)

2.2

Berechne die zu erwartende durchschnittliche Dauer für eine Gepäckkontrolle.

(4 BE)

Einer Fluggesellschaft wird ein automatisches Lesegerät für das Sortieren des Gepäcks angeboten, das eine Quote von weniger als $1\,\%$ an Lesefehlern verspricht. Die Fluggesellschaft ist skeptisch und will ihre Vermutung mit einer Irrtumswahrscheinlichkeit von maximal $2,5\,\%$ an 3000 gekennzeichneten Gepäckstücken testen lassen.

Bestimme die Entscheidungsregel für diesen Test.

Berechne die Wahrscheinlichkeit für einen Fehler 2. Art für diese Entscheidungsregel, wenn Lesefehler tatsächlich nur mit einer Wahrscheinlichkeit von $0,5\,\%$ auftreten.

(9P)

1.1

$X$ beschreibt die Anzahl der Gepäckstücke, die das Ziel Frankfurt haben und kann als binomialverteilt mit den Parametern $n=2$ und $p$ angenommen werden.

Es gilt:

$\begin{array}[t]{rll} P(X \leq 1)&=& 0,9375&\\[5pt] 1- P(X=2)&=& 0,9375 \end{array}$

Mit der Pfadregel ergibt sich die Wahrscheinlichkeit dafür, dass beide Gepäckstücke das Ziel Frankfurt haben, zu:

$P(X=2)= p\cdot p=p^2$

Es gilt also:

$\begin{array}[t]{rll} 1-P(X=2)&=& 0,9375&\quad \scriptsize \\[5pt] 1-p^2&=& 0,9375 &\quad \scriptsize \mid -1 \\[5pt] -p^2&=& -0,0625&\quad \scriptsize \mid \cdot (-1) \\[5pt] p^2&=& 0,0625 &\quad \scriptsize \mid \sqrt{\;} \\[5pt] p&=& 0,25 \end{array}$

Die Wahrscheinlichkeit, dass ein Gepäckstück das Ziel Frankfurt hat, beträgt somit $p = 0,25.$

1.2

$X$ beschreibt die Anzahl der Gepäckstücke mit Ziel Frankfurt und kann als binomialverteilt mit den Parametern $n = 10$ und $p = 0,25$ angenommen werden.

Es gilt also:

Rechenweg anzeigen

$P(X =3) \approx 25,03\,\%$

Mit einer Wahrscheinlichkeit von ca. $25,03\,\%$ haben unter 10 aufeinanderfolgenden Gepäckstücken genau 3 das Ziel Frankfurt.

1.3

Entscheidung

Die Wahrscheinlichkeit dafür, dass von 10 aufeinanderfolgenden Gepäckstücken keines das Ziel Frankfurt hat, ergibt sich mit:

$\begin{array}[t]{rll} P(X=0)&=&\pmatrix{10\\0} \cdot p^0\cdot (1-p)^{10} &\quad \scriptsize \\[5pt] &=&1\cdot1\cdot(1-p)^{10} &\quad \scriptsize \\[5pt] &=&(1-p)^{10} \end{array}$

Somit beschreibt $P_1 = (1-p)^{10}$ die passende Wahrscheinlichkeit.

Ereignis beschreiben

$p^{10}$ beschreibt die Wahrscheinlichkeit dafür, dass von 10 aufeinanderfolgenden Gepäckstücken genau 10 das Ziel Frankfurt haben.

Die Wahrscheinlichkeit $P_2$ beschreibt somit die Wahrscheinlichkeit des Gegenereignisses dazu, dass von 10 aufeinanderfolgenden Gepäckstücken genau 10 das Ziel Frankfurt haben. Dies entspricht dem Ereignis, dass nicht 10 der 10 aufeinanderfolgenden Gepäckstücke das Ziel Frankfurt haben.

Insgesamt ist $P_2$ also die Wahrscheinlichkeit dafür, dass unter $10$ aufeinanderfolgenden Gepäckstücken höchstens $9$ Stück das Ziel Frankfurt haben, bzw. dass mindestens eines ein anderes Ziel hat.

2.1

$E:$ Eindeutiges Ergebnis

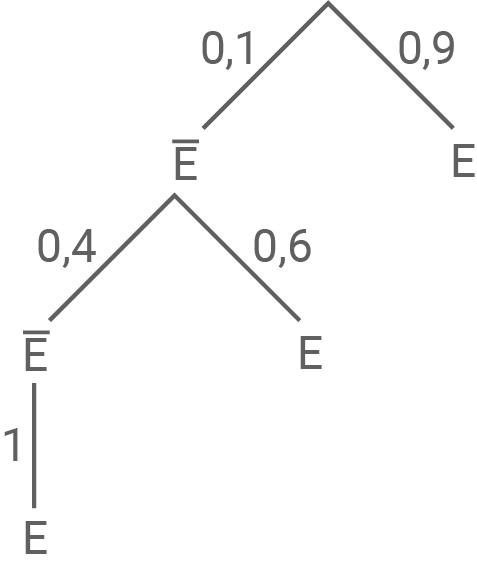
Ergebnis Kontrolle Gepaeckstueck Baumdiagramm

2.2

Es sind die folgenden Zeiten möglich:

Nach der ersten Kontrolle liegt bereits ein eindeutiges Ergebnis vor:
$10$ Sekunden

Das eindeutige Ergebnis erscheint nach der zweiten Kontrolle:
$10 + 30 +10$ Sekunden $= 50$ Sekunden

Das Gepäckstück muss alle drei Kontrollen durchlaufen:
$10+30+10 +30 + 5\cdot60$ Sekunden $= 380$ Sekunden

Damit ergibt sich:

$E(\text{Dauer}) = 10 \cdot p_{10} + 50\cdot p_{50} + 380\cdot p_{380}$

Aus dem Baumdiagramm folgt:

$p_{10} = 0,9$

$p_{50} = 0,1\cdot0,6 = 0,06$

$p_{380} = 0,1\cdot0,4\cdot1 =0,04$

Somit gilt:

Rechenweg anzeigen

$E(\text{Dauer})= 27,2 \; [\text{s}]$

Die zu erwartende durchschnittliche Dauer der Kontrolle beträgt folglich 27,2 Sekunden.

Entscheidungsregel für den Hypothesentest bestimmen

$H_0: p_0 \geq 0,01$

$H_1: p_1 \lt 0,01$

Wegen $p_0 \gt p_1$ muss ein rechtsseitiger Hypothesentest durchgeführt werden.

Gesucht ist das größte $k$ , für das gilt:

$P(X\leq k) \leq 0,025$

Hierbei beschreibt $X$ die Anzahl der Gepäckstücke, bei denen ein Lesefehler auftritt und kann als binomialverteilt mit den Parametern $p = 0,01$ und $n = 3000$ angenommen werden,

Der WTR liefert:

$\begin{array}[t]{rll} P(X\leq 20)&\approx& 0,035 & \\[5pt] &\gt& 0,025 \end{array}$

$\begin{array}[t]{rll} P(X \leq 19)&\approx& 0,021& \\[5pt] &\lt& 0,025 \end{array}$

Der Annahmebereich von $H_0$ ist somit gegeben durch $[20; 3000].$

Es dürfen folglich höchstens 19 Gepäckstücke im Test falschsortiert werden, damit die Fluggesellschaft ihre Nullhypothese ablehnt und dem Hersteller des Geräts vertraut.

Wahrscheinlichkeit für den Fehler 2. Art berechnen

Gesucht ist die Wahrscheinlichkeit des Fehlers 2. Art, wenn eine Fehlerquote von nur $0,5\,\%$ gilt.

Der Fehler 2. Art beschreibt das Ereignis, dass die Anzahl der falschsortierten Gepäckstücke in der Stichprobe mindestens $k = 20$ ist, die Hypothese $H_0: p \geq 0,01$ also angenommen wird, obwohl eigentlich die Wahrscheinlichkeit $p =0,005$ aus der Aufgabenstellung gilt.

$X$ beschreibt die Anzahl der falschsortierten Gepäckstücke und kann als binomialverteilt mit $n=3000$ und $p=0,005$ angenommen werden.

Es gilt:

$\begin{array}[t]{rll} P(X\geq 20)&=& 1-P(X \leq 19)& \quad \scriptsize \mid\; WTR \\[5pt] &\approx & 1-0,876 & \\[5pt] &= & 0,124 & \\[5pt] &= & 12,4% & \\[5pt] \end{array}$

Die Wahrscheinlichkeit für einen Fehler 2. Art beträgt ca. $12,4\,\%$ , wenn eigentlich eine Fehlerquote von $p =0,5\,\%$ gilt.

1.1

$X$ beschreibt die Anzahl der Gepäckstücke, die das Ziel Frankfurt haben und kann als binomialverteilt mit den Parametern $n=2$ und $p$ angenommen werden.

Es gilt:

$\begin{array}[t]{rll} P(X \leq 1)&=& 0,9375&\\[5pt] 1- P(X=2)&=& 0,9375 \end{array}$

Mit der Pfadregel ergibt sich die Wahrscheinlichkeit dafür, dass beide Gepäckstücke das Ziel Frankfurt haben, zu:

$P(X=2)= p\cdot p=p^2$

Es gilt also:

Die Wahrscheinlichkeit, dass ein Gepäckstück das Ziel Frankfurt hat, beträgt somit $p = 0,25.$

1.2

$X$ beschreibt die Anzahl der Gepäckstücke mit Ziel Frankfurt und kann als binomialverteilt mit den Parametern $n = 10$ und $p = 0,25$ angenommen werden.

Es gilt also:

Rechenweg anzeigen

$P(X =3) \approx 25,03\,\%$

Mit einer Wahrscheinlichkeit von ca. $25,03\,\%$ haben unter 10 aufeinanderfolgenden Gepäckstücken genau 3 das Ziel Frankfurt.

1.3

Entscheidung

Die Wahrscheinlichkeit dafür, dass von 10 aufeinanderfolgenden Gepäckstücken keines das Ziel Frankfurt hat, ergibt sich mit:

$\begin{array}[t]{rll} P(X=0)&=&\pmatrix{10\\0} \cdot p^0\cdot (1-p)^{10} &\quad \scriptsize \\[5pt] &=&1\cdot1\cdot(1-p)^{10} &\quad \scriptsize \\[5pt] &=&(1-p)^{10} \end{array}$

Somit beschreibt $P_1 = (1-p)^{10}$ die passende Wahrscheinlichkeit.

Ereignis beschreiben

$p^{10}$ beschreibt die Wahrscheinlichkeit dafür, dass von 10 aufeinanderfolgenden Gepäckstücken genau 10 das Ziel Frankfurt haben.

2.1

$E:$ Eindeutiges Ergebnis

2.2

Es sind die folgenden Zeiten möglich:

Nach der ersten Kontrolle liegt bereits ein eindeutiges Ergebnis vor:
$10$ Sekunden

Das eindeutige Ergebnis erscheint nach der zweiten Kontrolle:
$10 + 30 +10$ Sekunden $= 50$ Sekunden

Das Gepäckstück muss alle drei Kontrollen durchlaufen:
$10+30+10 +30 + 5\cdot60$ Sekunden $= 380$ Sekunden

Damit ergibt sich:

$E(\text{Dauer}) = 10 \cdot p_{10} + 50\cdot p_{50} + 380\cdot p_{380}$

Aus dem Baumdiagramm folgt:

$p_{10} = 0,9$

$p_{50} = 0,1\cdot0,6 = 0,06$

$p_{380} = 0,1\cdot0,4\cdot1 =0,04$

Somit gilt:

Rechenweg anzeigen

$E(\text{Dauer})= 27,2 \; [\text{s}]$

Die zu erwartende durchschnittliche Dauer der Kontrolle beträgt folglich 27,2 Sekunden.

Entscheidungsregel für den Hypothesentest bestimmen

$H_0: p_0 \geq 0,01$

$H_1: p_1 \lt 0,01$

Wegen $p_0 \gt p_1$ muss ein rechtsseitiger Hypothesentest durchgeführt werden.

Gesucht ist das größte $k$ , für das gilt:

$P(X\leq k) \leq 0,025$

Hierbei beschreibt $X$ die Anzahl der Gepäckstücke, bei denen ein Lesefehler auftritt und kann als binomialverteilt mit den Parametern $p = 0,01$ und $n = 3000$ angenommen werden,

Der WTR liefert:

$\begin{array}[t]{rll} P(X\leq 20)&\approx& 0,035 & \\[5pt] &\gt& 0,025 \end{array}$

$\begin{array}[t]{rll} P(X \leq 19)&\approx& 0,021& \\[5pt] &\lt& 0,025 \end{array}$

Der Annahmebereich von $H_0$ ist somit gegeben durch $[20; 3000].$

Es dürfen folglich höchstens 19 Gepäckstücke im Test falschsortiert werden, damit die Fluggesellschaft ihre Nullhypothese ablehnt und dem Hersteller des Geräts vertraut.

Wahrscheinlichkeit für den Fehler 2. Art berechnen

Gesucht ist die Wahrscheinlichkeit des Fehlers 2. Art, wenn eine Fehlerquote von nur $0,5\,\%$ gilt.

$X$ beschreibt die Anzahl der falschsortierten Gepäckstücke und kann als binomialverteilt mit $n=3000$ und $p=0,005$ angenommen werden.

Es gilt:

$\begin{array}[t]{rll} P(X\geq 20)&=& 1-P(X \leq 19)& \quad \scriptsize \mid\; WTR \\[5pt] &\approx & 1-0,876 & \\[5pt] &= & 0,124 & \\[5pt] &= & 12,4% & \\[5pt] \end{array}$

Die Wahrscheinlichkeit für einen Fehler 2. Art beträgt ca. $12,4\,\%$ , wenn eigentlich eine Fehlerquote von $p =0,5\,\%$ gilt.