B2 - Analytische Geometrie
1
Eine Fabrikhalle soll in einen gleichmäßig ansteigenden Hang hinein gebaut werden. Dazu wird aus dem Hang Erde abgetragen. Der entstehende Einschnitt in den Hang wird im Folgenden als Baugrube bezeichnet. Das Gelände vor der Baugrube ist eben und liegt in der 
-Ebene.
Der Übergang von der -Ebene in den Hang wird von der Geraden 
beschrieben, die durch die Punkte 
und 
verläuft (Material). Diese Punkte sind gleichzeitig die beiden vorderen Eckpunkte der rechteckigen Grundfläche der Baugrube. Der Punkt 
ist ein weiterer Eckpunkt dieser Grundfläche.
Modellhaft kann angenommen werden, dass der Hang in einer Ebene 
liegt. In dieser Ebene liegen auch die beiden oberen Eckpunkte 
und 
der Baugrube.
Alle Angaben erfolgen in Metern.
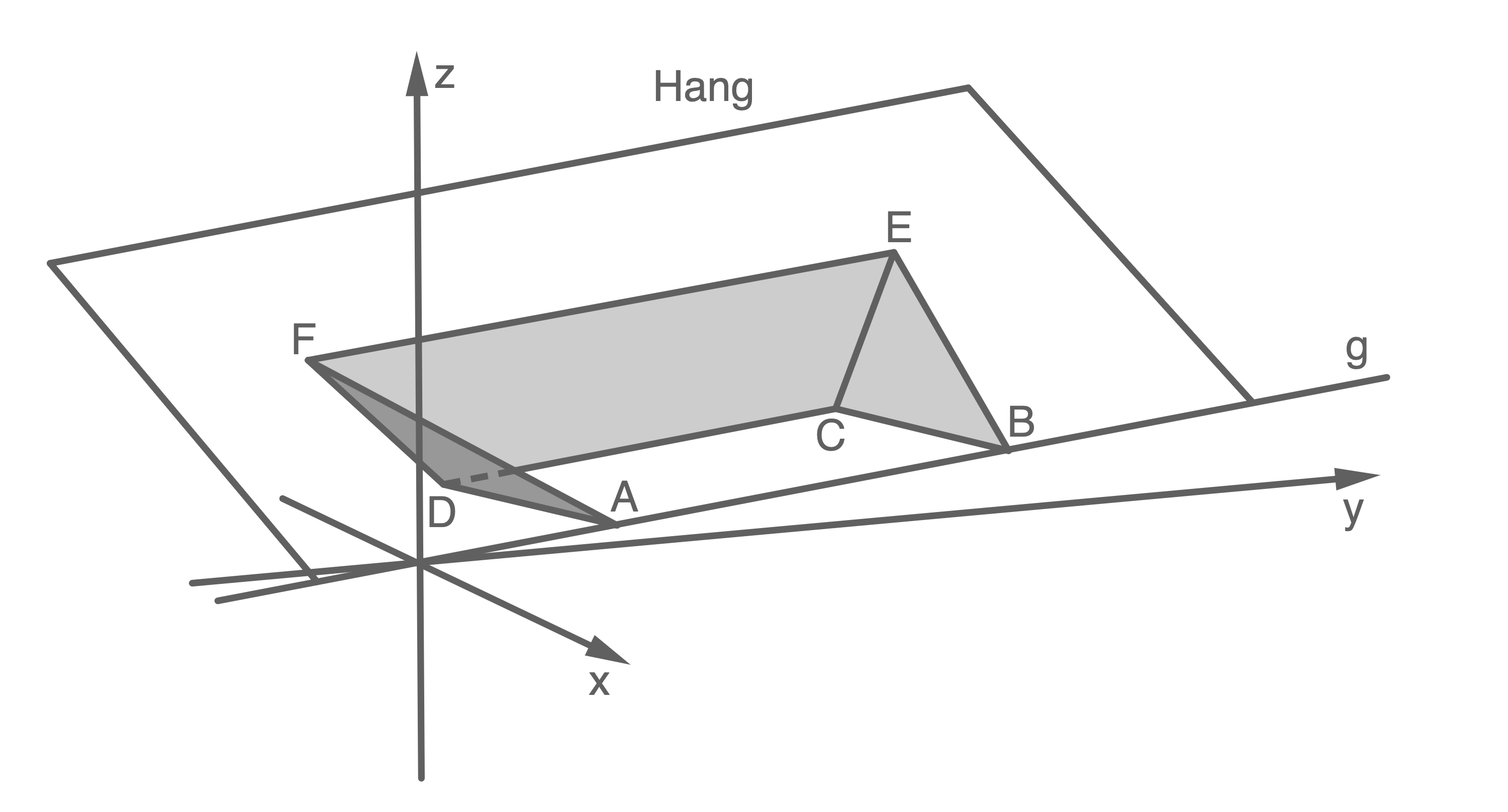
Hang und Baugrube
1.1
Berechne den fehlenden Eckpunkt 
der Grundfläche 
der Baugrube.
Bestätige durch Rechnung, dass diese Grundfläche bei
einen rechten Winkel besitzt.
Bestätige durch Rechnung, dass diese Grundfläche bei
(4 BE)
1.2
Gib eine Gleichung der Hangebene in Parameterform an und bestimme eine Koordinatengleichung dieser Ebene.
[zur Kontrolle: 
]
(6 BE)
1.3
Von einem festen Messpunkt 
außerhalb der Baustelle wird der obere Eckpunkt der Baugrube über den Vektor 
anvisiert.
Bestimme die Koordinaten des Punktes.
Bestimme die Koordinaten des Punktes
(4 BE)
1.4
Die Punkte 
, , und 
sind die Eckpunkte der „hinteren Wand“ der Baugrube. Sie liegen in der steil abfallenden Ebene 
.
Eine Koordinatengleichung dieser Ebene lautet
.
Nach Bauvorschrift darf eine solche Ebene gegenüber der Grundfläche höchstens einen Steigungswinkel von
besitzen.
Untersuche, ob die Ebene die Vorgabe der Bauvorschrift erfüllt.
Eine Koordinatengleichung dieser Ebene lautet
Nach Bauvorschrift darf eine solche Ebene gegenüber der Grundfläche höchstens einen Steigungswinkel von
Untersuche, ob die Ebene
(3 BE)
2
Zwei Meter unterhalb des Mittelpunktes der Grundfläche beginnt die Entwässerungsleitung des gesamten Bauvorhabens. Sie hat ein gleichmäßiges Gefälle von 
.
Die Gerade, die sich durch die Projektion der Entwässerungsleitung in die-Ebene ergibt, hat den Richtungsvektor 
.
Die Gerade, die sich durch die Projektion der Entwässerungsleitung in die
2.1
Bestimme für den dreidimensionalen Raum die Gleichung der Geraden 
, die den Verlauf der Entwässerungsleitung beschreibt.
(5 BE)
2.2
Der öffentliche Hauptkanal, an den die Entwässerungsleitung angeschlossen werden soll, lässt sich mithilfe folgender Geradengleichung modellhaft beschreiben:
Da sich die Entwässerungsleitung und der Hauptkanal nicht schneiden, ist ein vertikaler, in Richtung der
-Achse verlaufender Fallschacht einzubauen, der die Entwässerungsleitung mit dem Hauptkanal verbindet.
Ermittle die Höhe dieses Fallschachtes.
Da sich die Entwässerungsleitung und der Hauptkanal nicht schneiden, ist ein vertikaler, in Richtung der
Ermittle die Höhe dieses Fallschachtes.
(4 BE)
3
Entwickle eine Lösungsstrategie, mit der das Volumen des Erdaushubs für die Baugrube berechnet werden kann. Erläutere die einzelnen Schritte deines Lösungsweges.
Eine Durchführung der entsprechenden Rechnungen ist nicht erforderlich.
Eine Durchführung der entsprechenden Rechnungen ist nicht erforderlich.
(4P)
1
1.1
Koordinaten von berechnen
Da die Grundfläche laut Aufgabenstellung rechteckig ist, gilt, dass die jeweils gegenüberliegenden Seiten parallel und gleich lang sind.
Es muss also gelten:
Damit folgt der fehlende Eckpunkt mit 
.
Rechten Winkel überprüfen
Der Winkel bei entspricht dem Winkel zwischen den Verbindungsvektoren 
und 
Ist das Skalarprodukt zweier Vektoren gleich Null, so stehen diese beiden senkrecht aufeinander und bilden somit einen rechten Winkel.
Damit ist gezeigt, dass die Grundfläche bei einen rechten Winkel besitzt.
1.2
Parameterform angeben
Aus den Punkten , 
und in der Hangebene kann eine Gleichung der Ebene in Parameterform aufgestellt werden. Eine mögliche solche Gleichung in Parameterform ist:
Die Vektoren 
und wurden bereits in 1.1 berechnet. Der Vektor 
folgt mit:
![\(\begin{array}[t]{rll}
\overrightarrow{AF}&=& \overrightarrow{OF}-\overrightarrow{OA}& \\[5pt]
&=& \begin{pmatrix}-45\\ 5\\ 15\end{pmatrix} - \begin{pmatrix}-10\\ 30\\ 0\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}-35\\ -25\\ 15\end{pmatrix}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/8172c892b6cefeaddee48b5ae51f3c9dd93b8bafed9a10d9a778ae1ac2a287bc?color=5a5a5a)
Damit lautet eine mögliche Gleichung in Parameterform:
Koordinatenform bestimmen
Mit dem Vektorproduktder der beiden Richtungsvektoren der Ebene kann ein Normalenvektor 
berechnet werden. Dieser kann durch folgenden Befehl mit dem CAS bestimmt werden:
Es folgt ein Normalenvektor der Ebene mit 
Eine mögliche Gleichung in Koordinatenform lautet somit beispielsweise:
Da die Ebene durch den Ursprung verläuft, gilt 
. Somit lautet eine Ebenengleichung in Koordinatenform:
menu 
7: Matrix und Vektor C: Vektor 2: Kreuzprodukt
Nach Eingabe der beiden Vektoren kann nun das Kreuzprodukt bestimmt werden:
1.3
Der Punkt befindet sich auf der Geraden 
, welche durch den Punkt 
entlang des Vektors 
verläuft. Die Geradengleichung von lautet somit:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=&\overrightarrow{OP} + s \cdot \overrightarrow{v} &\\[5pt]
\overrightarrow{x}&=& \begin{pmatrix}30\\ 20\\ 5\end{pmatrix} + \begin{pmatrix}21\\ 15\\ 2\end{pmatrix} \cdot s&\\[5pt]
\overrightarrow{x}&=&\begin{pmatrix}30 -21 \cdot s\\ 20 + 15 \cdot s\\ 5 + 2 \cdot s\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/d4b4256da901557b1924b7c2be5667a164466abd98b5607c0e265c537de24166?color=5a5a5a)
Da der Punkt auch in der Ebene liegt, entspricht er dem Schnittpunkt der Geraden mit der Ebene .
Dieser kann durch Einsetzen der Geradengleichung in die Koordinatengleichung von bestimmt werden:
Die Koordinaten von folgen mit:
![\(\begin{array}[t]{rll}
\overrightarrow{OE} &=& \begin{pmatrix}30 -21 \cdot 5\\ 20 + 15 \cdot 5\\ 5 + 2 \cdot 5\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}30 -105\\ 20 + 75\\ 5 + 10\end{pmatrix}& \\[5pt]
&=& \begin{pmatrix}-75\\ 95\\ 15\end{pmatrix}& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/97f95ddb1ed318a260dd1bf0e5d091a454a029400fe6a3adc011f324f17b255f?color=5a5a5a)
Der gesuchte Punkt ist somit gegeben durch 
1.4
Der gesuchte Winkel 
entspricht dem Winkel zwischen der -Ebene und der Ebene .
Ein Normalenvektor 
der 
-
-Ebene ist beispielsweise 
Ein Normalenvektor 
der Ebene kann direkt aus der gegebenen Koordinatengleichung abgelesen werden.
Mit der Formel für Schnittwinkel folgt nun:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=& \dfrac{\left| \overrightarrow{n_J} \circ \overrightarrow{n_{xy}} \right|}{ \left| \overrightarrow{n_J} \right| \cdot \left| \overrightarrow{n_{xy}} \right|}& \\[5pt]
\cos(\alpha)&=& \dfrac{\left| \left(\begin{array}{c}3\\ 1\\ 2\end{array}\right) \circ \left(\begin{array}{c}0\\0\\1\end{array}\right) \right|}{ \left|\left(\begin{array}{c}3\\ 1\\ 2\end{array}\right) \right| \cdot \left|\left(\begin{array}{c}0\\0\\1\end{array}\right) \right|}& \\[5pt]
\cos(\alpha)&=& \dfrac{2}{\sqrt{14}}& \quad \scriptsize \mid \arccos\\[5pt]
\alpha&=& \cos^{-1}\left(\dfrac{2}{\sqrt{14}}\right)& \\[5pt]
\alpha&\approx& 57,69^{\circ}
\end{array}\)](https://mathjax.schullv.de/6fcbbee109cef09dcb1becb51af37235d461c32c0cf0470dc9242769ef556acb?color=5a5a5a)
Der Steigungswinkel beträgt somit etwa 
und überschreitet folglich nicht die Bauvorschrift von 
2
2.1
1. Schritt: Punkt auf der Geraden bestimmen
Der Beginn der Entwässerungsleitung liegt laut Aufgabenstellung 2 Meter unter dem Mittelpunkt 
des Rechtecks und entsprechend auf der Geraden .
Der Mittelpunkt der Grundfläche kann mit Hilfe der Diagonalen berechnet werden:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OA} + \dfrac{1}{2} \cdot \overrightarrow{AC} &\\[5pt]
&=& \begin{pmatrix}-10\\ 30\\ 0\end{pmatrix} + \dfrac{1}{2} \cdot \begin{pmatrix}-50\\ 50\\ 0\end{pmatrix}&\\[5pt]
&=& \begin{pmatrix}-10\\ 30\\ 0\end{pmatrix} + \begin{pmatrix}-25\\25\\ 0\end{pmatrix}&\\[5pt]
&=&\begin{pmatrix}-35\\55\\0\end{pmatrix}
\end{array}\)](https://mathjax.schullv.de/bfe62dfe5648e7bd4553fd376995b91dfa7d3a98b26c3ee3c06651722ecc4075?color=5a5a5a)
Nach Aufgabenstellung befindet sich der Punkt 2 Meter unter dem Mittelpunkt 
ist somit gegeben durch:
2. Schritt: Richtung der Geraden bestimmen
Die - und -Koordinaten sind bereits durch 
gegeben. Damit lautet der Richtungsvektor der Geraden : 
.
Da die Leitung ein gleichmäßiges Gefälle von hat, geht die Leitung auf einer Länge von 100 Metern in der -Ebene 2 Meter nach unten. Die Länge des Richtungsvektor in der -Ebene entspricht dem Betrag des Vektors 
Auf einer Länge von 5 Metern geht die Leitung bei einem Gefälle von somit um 0,1 Meter nach unten.
Damit ist ein Richtungsvektor der Geraden gegeben durch 
.
Insgesamt folgt eine Geradngleichung also mit:
2.2
1. Schritt: Lage des Fallschachts in der -Ebene bestimmen
Da der Fallschacht in -Richtung verläuft, hat dieser feste - und -Koordinaten. Die Berührungspunkte 
und 
der Geraden und 
mit dem Fallschacht müssen folglich die selben - und -Koordinaten besitzen.
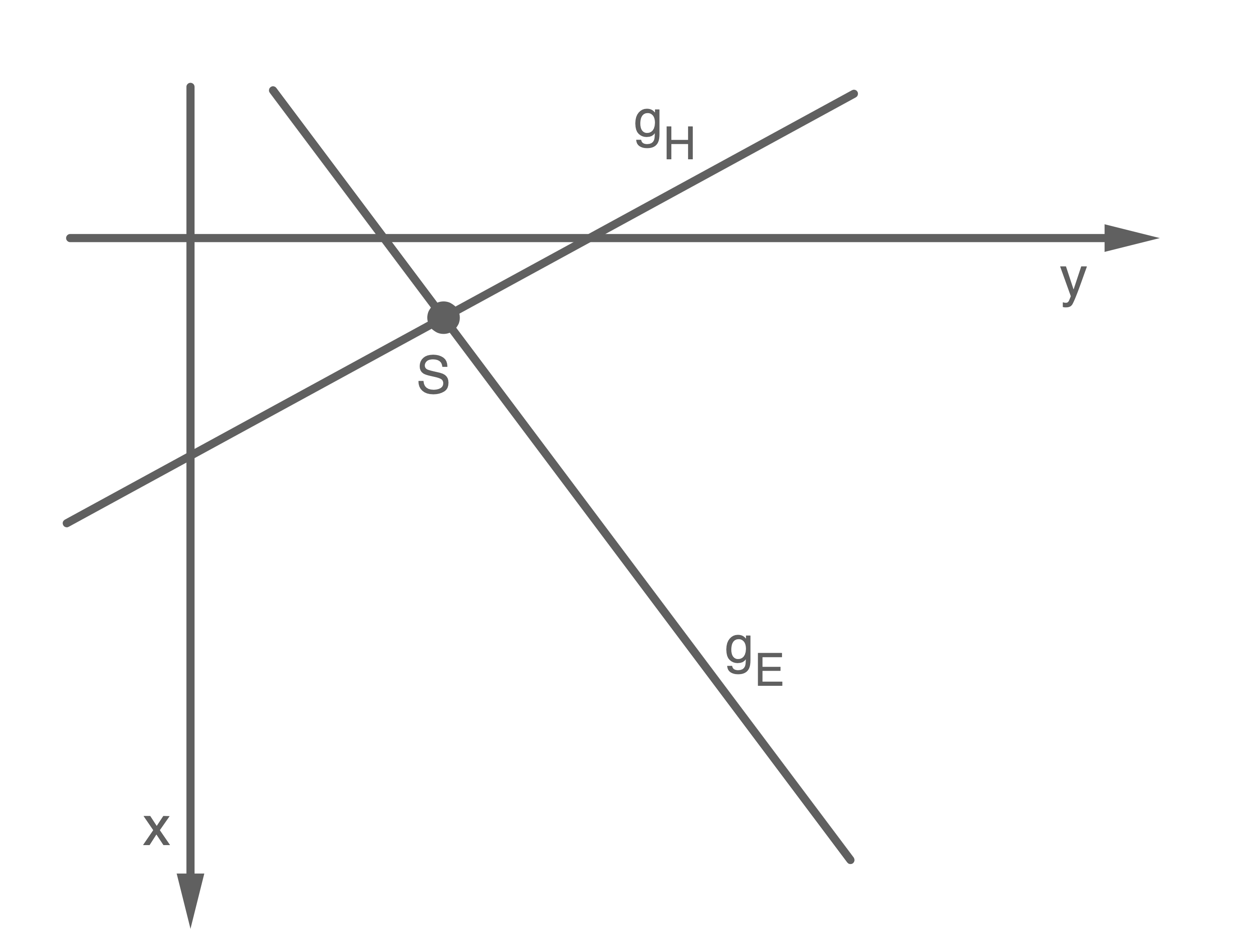Durch Gleichsetzen der - und -Komponenten der Geraden und ergibt sich folgendes lineares Gleichungssystem:
![\(\begin{array}{lrll}
\text{I}\quad&-35 +4s&=65 -2r\\[5pt]
\text{II}\quad&55 +3s&=20+4r
\end{array}\)](https://mathjax.schullv.de/7ea664b6bea3f9db7fb50de1e33d5b9896a6a1aa9b240fc607b15c597ac141f3?color=5a5a5a)
Dieses kann mit dem CAS gelöst werden:
und 
sowie der dazugehörigen Gleichungen ergibt sich:
Lösungen des Gleichungssystems sind folglich 
und 
Damit ergeben sich die - und -Koordinaten:
Der Projektionspunkt besitzt somit die Koordinaten 
.
2. Schritt: Berührungspunkte bestimmen
Die -Koordinaten der Ortsvektoren der Berührungspunkte und mit dem Fallschacht lassen sich durch Wählen eines passenden Werts für die Parameter und bestimmen. Diese müssen so gewählt werden, dass die - und -Koordinaten mit dem Projektionspunkt 
übereinstimmen.
Für 
und folgt:
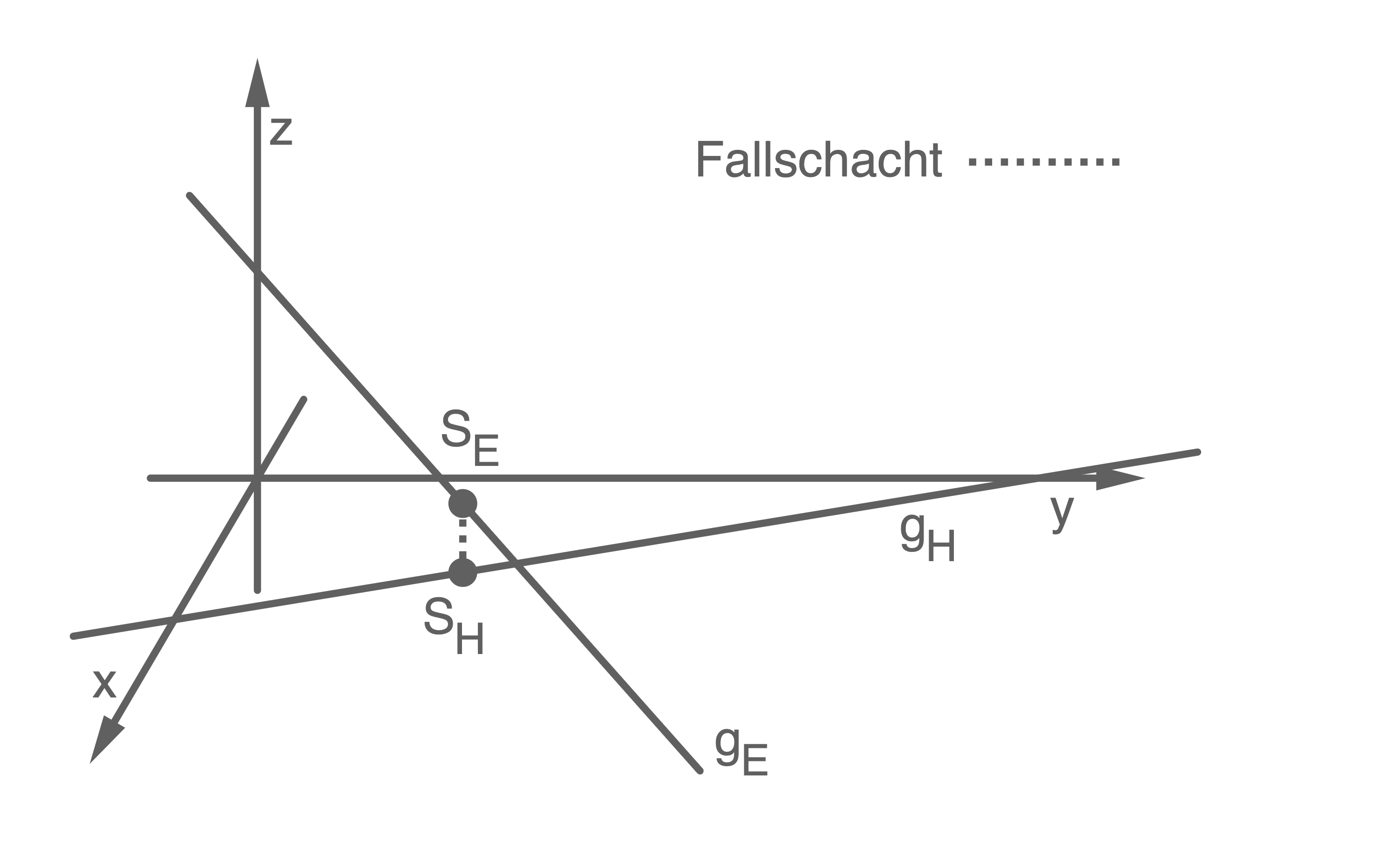3. Schritt: Höhe des Fallschachts berechnen
Die Höhe des Fallschachts entspricht der Länge der Verbindungsstrecke 
:
![\(\begin{array}[t]{rll}
\left|\overrightarrow{S_ES_H}\right|&=&\left|\begin{pmatrix}25\\ 100\\ -3,5\end{pmatrix} - \begin{pmatrix}25\\ 100\\ -3,7\end{pmatrix} \right| &\\[5pt]
&=&\left|\begin{pmatrix}0\\ 0\\ -0,2\end{pmatrix}\right| &\\[5pt]
&=& 0,2 \; [\,\text{m}]
\end{array}\)](https://mathjax.schullv.de/9025fe6534af9b42c3e4472b25cda41cbb42e5bfa556fb5ef3afdc936886037c?color=5a5a5a)
Der Fallschacht ist also 0,2 Meter hoch.
Lage der Geraden in der -Ebene
menu 3: Algebra 7 1: Gleichungssystem lösen...
Nach Eingabe der Variablen
3
Lösungsstrategie
Der Erdaushub kann in 3 Teilbereiche aufgeteilt und die Volumina der Teilbereiche jeweils einzeln bestimmt werden. Die äußeren Teilbereiche entsprechen hierbei einer Pyramide, der mittlere Teilbereich einem Prisma.
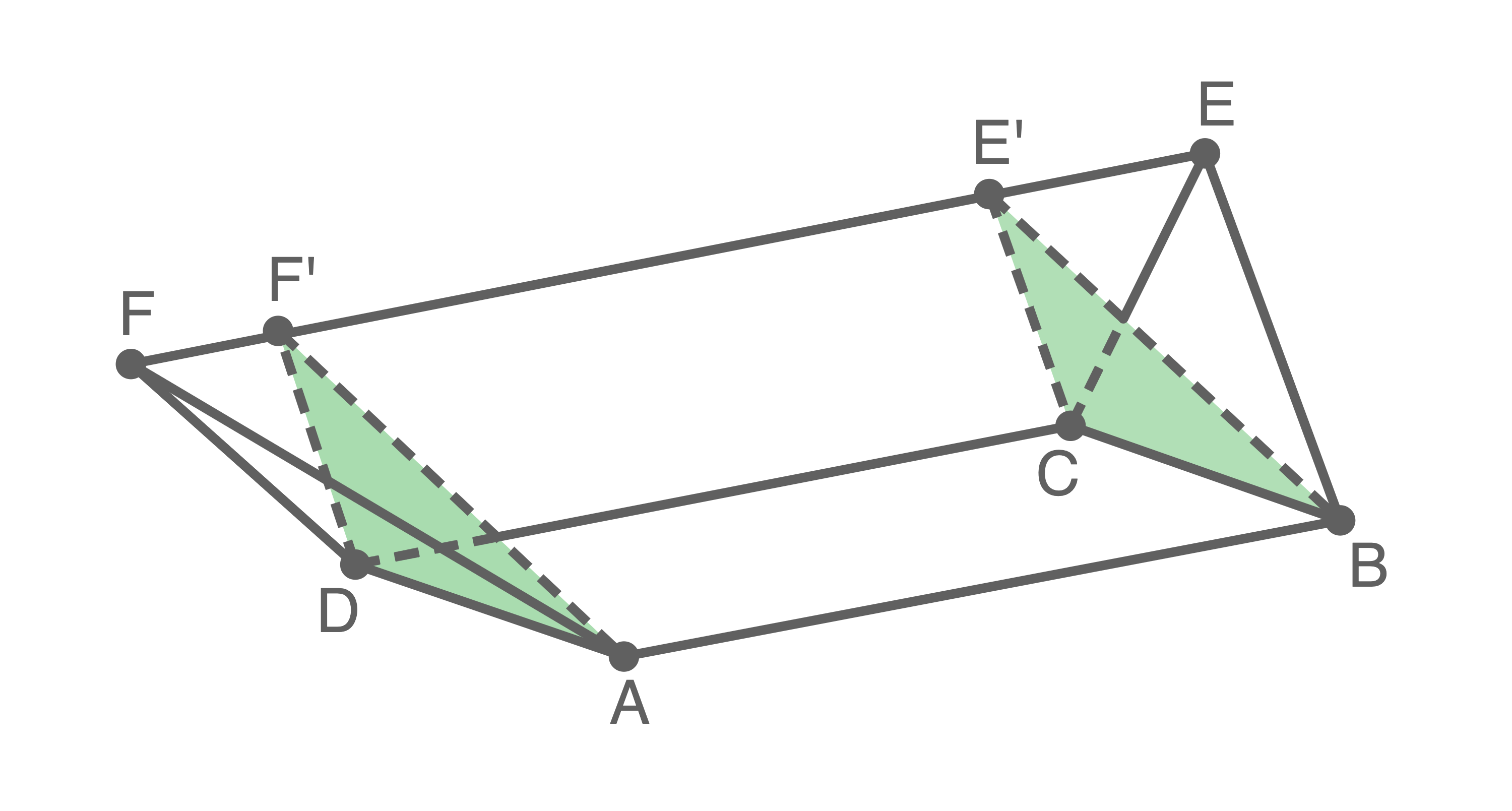1. Schritt: Aufteilen der Baugrube in drei Teilbereiche
Es können die beiden Punkte 
und 
definiert werden, welche auf der Verbindungsstrecke 
liegen und bei Projektion in die --Ebene auf einer Geraden mit und beziehungsweise mit und liegen.
In der -Ebene bilden sich so zwei Dreiecke 
und 
. Diese Dreiecke teilen den Erdaushub in die drei Teilstücke. Die Flächen der Dreiecke sind gleich groß und können wie folgt berechnet werden:
2. Schritt: Volumen 
des mittleren Teilstücks bestimmen
Die Grund- und Deckfläche des Prismas entsprechen beiden Dreiecksflächen, die parallel und kongruent sind. Das Volumen des mittleren Teilstücks berechnet sich nun mit der Grundläche, also der Fläche des Dreiecks, und der Höhe des Prismas,welche der Grundseite beziehungsweise 
entspricht:
3. Schritt: Volumen der äußeren Teilstücke bestimmen
Durch Drehen des Teilstücks am Eckpunkt auf die Dreiecksfläche erhält man eine Pyramide mit dem Dreieck als Grundfläche und dem Punkt als Spitze. Die Spitze liegt über dem Punkt , somit beträgt die Höhe der Pyramide genau 
.
Für das Volumen 
einer Pyramide folgt also:
Analog ergibt sich 
.
4. Schritt: Gesamtvolumen 
bestimmen
1
1.1
Koordinaten von berechnen
Da die Grundfläche laut Aufgabenstellung rechteckig ist, gilt, dass die jeweils gegenüberliegenden Seiten parallel und gleich lang sind.
Es muss also gelten:
Damit folgt der fehlende Eckpunkt mit .
Rechten Winkel überprüfen
Der Winkel bei entspricht dem Winkel zwischen den Verbindungsvektoren und Ist das Skalarprodukt zweier Vektoren gleich Null, so stehen diese beiden senkrecht aufeinander und bilden somit einen rechten Winkel.
Damit ist gezeigt, dass die Grundfläche bei einen rechten Winkel besitzt.
1.2
Parameterform angeben
Aus den Punkten , und in der Hangebene kann eine Gleichung der Ebene in Parameterform aufgestellt werden. Eine mögliche solche Gleichung in Parameterform ist:
Die Vektoren und wurden bereits in 1.1 berechnet. Der Vektor folgt mit:
Damit lautet eine mögliche Gleichung in Parameterform:
Koordinatenform bestimmen
Mit dem Vektorproduktder der beiden Richtungsvektoren der Ebene kann ein Normalenvektor berechnet werden. Dieser kann durch folgenden Befehl mit dem CAS bestimmt werden:
Es folgt ein Normalenvektor der Ebene mit
Eine mögliche Gleichung in Koordinatenform lautet somit beispielsweise:
Da die Ebene durch den Ursprung verläuft, gilt . Somit lautet eine Ebenengleichung in Koordinatenform:
Interaktiv Vektor crossP
Nach Eingabe der beiden Vektoren kann nun das Kreuzprodukt bestimmt werden:
1.3
Der Punkt befindet sich auf der Geraden , welche durch den Punkt entlang des Vektors verläuft. Die Geradengleichung von lautet somit:
Da der Punkt auch in der Ebene liegt, entspricht er dem Schnittpunkt der Geraden mit der Ebene .
Dieser kann durch Einsetzen der Geradengleichung in die Koordinatengleichung von bestimmt werden:
Die Koordinaten von folgen mit:
Der gesuchte Punkt ist somit gegeben durch
1.4
Der gesuchte Winkel entspricht dem Winkel zwischen der -Ebene und der Ebene .
Ein Normalenvektor der --Ebene ist beispielsweise Ein Normalenvektor der Ebene kann direkt aus der gegebenen Koordinatengleichung abgelesen werden.
Mit der Formel für Schnittwinkel folgt nun:
Der Steigungswinkel beträgt somit etwa und überschreitet folglich nicht die Bauvorschrift von
2
2.1
1. Schritt: Punkt auf der Geraden bestimmen
Der Beginn der Entwässerungsleitung liegt laut Aufgabenstellung 2 Meter unter dem Mittelpunkt des Rechtecks und entsprechend auf der Geraden .
Der Mittelpunkt der Grundfläche kann mit Hilfe der Diagonalen berechnet werden:
Nach Aufgabenstellung befindet sich der Punkt 2 Meter unter dem Mittelpunkt
ist somit gegeben durch:
2. Schritt: Richtung der Geraden bestimmen
Die - und -Koordinaten sind bereits durch gegeben. Damit lautet der Richtungsvektor der Geraden : .
Da die Leitung ein gleichmäßiges Gefälle von hat, geht die Leitung auf einer Länge von 100 Metern in der -Ebene 2 Meter nach unten. Die Länge des Richtungsvektor in der -Ebene entspricht dem Betrag des Vektors
Auf einer Länge von 5 Metern geht die Leitung bei einem Gefälle von somit um 0,1 Meter nach unten.
Damit ist ein Richtungsvektor der Geraden gegeben durch .
Insgesamt folgt eine Geradngleichung also mit:
2.2
1. Schritt: Lage des Fallschachts in der -Ebene bestimmen
Da der Fallschacht in -Richtung verläuft, hat dieser feste - und -Koordinaten. Die Berührungspunkte und der Geraden und mit dem Fallschacht müssen folglich die selben - und -Koordinaten besitzen.
Durch Gleichsetzen der - und -Komponenten der Geraden und ergibt sich folgendes lineares Gleichungssystem:
Dieses kann mit dem CAS gelöst werden:
und sowie der dazugehörigen Gleichungen ergibt sich:
Lösungen des Gleichungssystems sind folglich und
Damit ergeben sich die - und -Koordinaten:
Der Projektionspunkt besitzt somit die Koordinaten .
2. Schritt: Berührungspunkte bestimmen
Die -Koordinaten der Ortsvektoren der Berührungspunkte und mit dem Fallschacht lassen sich durch Wählen eines passenden Werts für die Parameter und bestimmen. Diese müssen so gewählt werden, dass die - und -Koordinaten mit dem Projektionspunkt übereinstimmen.
Für und folgt:
3. Schritt: Höhe des Fallschachts berechnen
Die Höhe des Fallschachts entspricht der Länge der Verbindungsstrecke :
Der Fallschacht ist also 0,2 Meter hoch.
Lage der Geraden in der -Ebene
Keyboard 
Nach Eingabe der Variablen
3
Lösungsstrategie
Der Erdaushub kann in 3 Teilbereiche aufgeteilt und die Volumina der Teilbereiche jeweils einzeln bestimmt werden. Die äußeren Teilbereiche entsprechen hierbei einer Pyramide, der mittlere Teilbereich einem Prisma.
1. Schritt: Aufteilen der Baugrube in drei Teilbereiche
Es können die beiden Punkte und definiert werden, welche auf der Verbindungsstrecke liegen und bei Projektion in die --Ebene auf einer Geraden mit und beziehungsweise mit und liegen.
In der -Ebene bilden sich so zwei Dreiecke und . Diese Dreiecke teilen den Erdaushub in die drei Teilstücke. Die Flächen der Dreiecke sind gleich groß und können wie folgt berechnet werden:
2. Schritt: Volumen des mittleren Teilstücks bestimmen
Die Grund- und Deckfläche des Prismas entsprechen beiden Dreiecksflächen, die parallel und kongruent sind. Das Volumen des mittleren Teilstücks berechnet sich nun mit der Grundläche, also der Fläche des Dreiecks, und der Höhe des Prismas,welche der Grundseite beziehungsweise entspricht:
3. Schritt: Volumen der äußeren Teilstücke bestimmen
Durch Drehen des Teilstücks am Eckpunkt auf die Dreiecksfläche erhält man eine Pyramide mit dem Dreieck als Grundfläche und dem Punkt als Spitze. Die Spitze liegt über dem Punkt , somit beträgt die Höhe der Pyramide genau .
Für das Volumen einer Pyramide folgt also:
Analog ergibt sich .
4. Schritt: Gesamtvolumen bestimmen