C1.2 - Lineare Algebra/Analytische Geometrie

In einem kartesischen Koordinatensystem sind die Punkte $A(0\mid 0\mid 0),$ $B(2\mid 0\mid 0),$ $C(2\mid 3\mid 0),$ $D(0\mid 3\mid 0),$ $E(0\mid 0\mid 3),$ $F(2\mid 0\mid 2)$ und $H(0\mid 3\mid 1)$ die Eckpunkte eines Körpers $K$ mit rechteckiger Grundfläche (Material). Alle diesen Körper $K$ begrenzende Flächen sind eben.

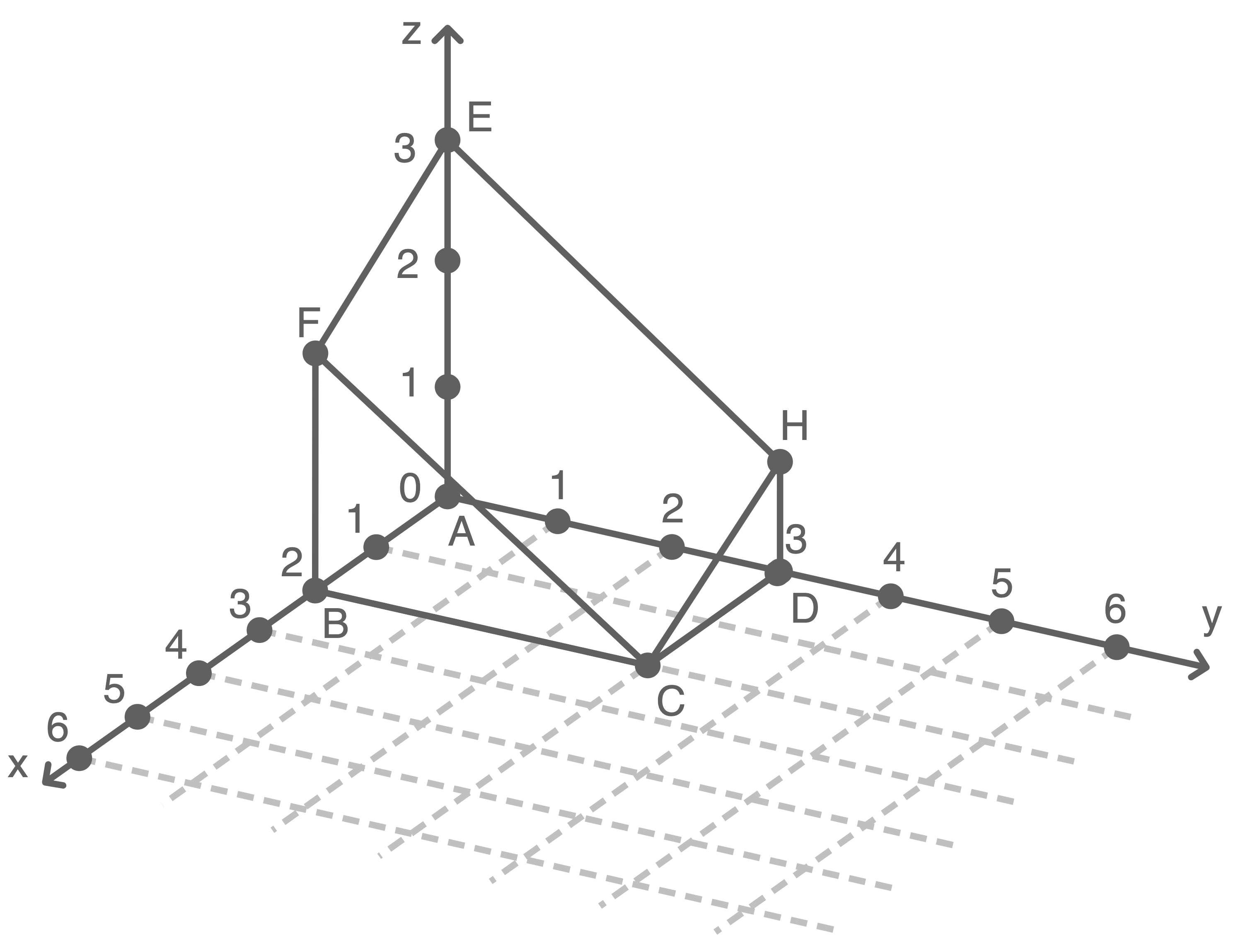
Material

1.1

Zeige, dass das Viereck $EFCH$ ein Parallelogramm, aber kein Rechteck ist.

(4 BE)

1.2

Gib eine Parametergleichung der Ebene $J$ an, in der die Fläche $EFCH$ liegt.
Bestimme eine zugehörige Koordinatengleichung.
[Zur Kontrolle: Eine mögliche Koordinatengleichung lautet $J: 3x+4y+6z=18$ .]

(5 BE)

1.3

Berechne den Neigungswinkel der Ebene $J$ gegenüber der $x$ - $y$ -Ebene.

(3 BE)

1.4

Ein Schnittpunkt der Ebene $J$ mit den Koordinatenachsen ist der Punkt $E$ . Die anderen beiden Schnittpunkte haben die Koordinaten $S_x(6\mid 0 \mid 0)$ und $S_y(0 \mid 4,5 \mid 0)$ .
Beschreibe, wie man die Koordinaten des Punktes $S_y$ berechnen kann.
Zeichne die Punkte $S_x$ und $S_y$ sowie die Kanten der Pyramide $AS _{ x } S _{ y } E$ in das Material ein.

(4 BE)

1.5

Der Körper $K$ ist ein Teilkörper der Pyramide $AS_xS_yE$ . Berechne den prozentualen Anteil des Volumens des Körpers $K$ am Volumen der Pyramide $AS_xS_yE$ .

(5 BE)

Gegeben ist die Geradenschar

Geradenschar anzeigen

1.6

Zeige rechnerisch, dass alle Geraden der Schar in der Ebene $J$ liegen.

(3 BE)

1.7

Berechne den Wert des Parameters $a$ , für den die zugehörige Gerade der Schar durch den Punkt $C$ verläuft.
Begründe, dass für den berechneten Wert des Parameters $a$ die zugehörige Gerade der Schar die gesamte Strecke $\overline{ EC }$ enthält.
[Zur Kontrolle: $a =0,5$ ]

(4 BE)

1.8

Bestimme alle Werte des Parameters $a$ , für welche die zugehörigen Geraden der Schar mehr als einen Punkt mit dem Parallelogramm $EFCH$ gemeinsam haben.

(4 BE)

1.9

Erläutere die Ansätze und deren geometrische Bedeutungen in den Zeilen $\,\text I$ und $\,\text {II}$ und gib die geometrische Bedeutung des Ergebnisses in Zeile $\,\text {III}$ an.

Gleichungssystem anzeigen

(6 BE)

Ein Künstler will eine auf ebenem Boden stehende Betoninstallation herstellen, die als Sonnenuhr fungiert. Der Betonkörper entspricht dabei dem oben beschriebenen Körper $K$ .
Die Sonnenuhr besteht neben dem Betonkörper aus einer massiven Stange, die einen Schatten auf den Betonkörper bzw. auf den Boden wirft. Die Stange wird im Folgenden als Strecke modelliert.
Der ebene Boden wird durch die $x$ - $y$ -Ebene dargestellt; eine Einheit entspricht einem Meter.

2.1

Die Stange ist insgesamt $3\,\text{m}$ lang und wird senkrecht zur Fläche $EFCH$ im Betonkörper verankert, ein Teil der Stange steckt also im Betonkörper. Die Stange endet im Modell im Punkt $Q (1,5\mid 2\mid 3)$ außerhalb des Betonkörpers.
Berechne die Koordinaten des anderen Endpunktes der Stange, der innerhalb des Betonkörpers liegt.

(5 BE)

2.2

Zu einem bestimmten Zeitpunkt fällt der Schatten des Punktes $Q$ auf den Punkt $H$ .
Ermittle einen Vektor, der zum betrachteten Zeitpunkt die Richtung der parallel einfallenden Sonnenstrahlen beschreibt.

(1 BE)

2.3

Zu einem anderen Zeitpunkt kann die Richtung der parallel einfallenden Sonnenstrahlen durch den Vektor $\overrightarrow{ v }=\left(\begin{array}{c}-1,5 \\ 0 \\ -1\end{array}\right)$ beschrieben werden. Der Schatten des Punktes $Q$ fällt nun auf den Boden.
Berechne die Koordinaten des Schattenpunktes $\(Q$ .
Bestimme die Koordinaten des Punktes der Kante $\overline{ EH }$ , der im Schatten der Stange liegt.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Parallelogramm nachweisen

$\overrightarrow{EF}=\pmatrix{2\\0\\2}-\pmatrix{0\\0\\3}=\pmatrix{2\\0\\-1}$

$\overrightarrow{CH}=\pmatrix{0\\3\\1}-\pmatrix{2\\3\\0}=\pmatrix{-2\\0\\1}$

$\overrightarrow{EH}=\pmatrix{0\\3\\1}-\pmatrix{0\\0\\3}=\pmatrix{0\\3\\-2}$

$\overrightarrow{FC}=\pmatrix{2\\3\\0}-\pmatrix{2\\0\\2}=\pmatrix{0\\3\\-2}$

Da $\overrightarrow{EF}=\overrightarrow{CH}$ und somit auch $|\overrightarrow{EF}|=|\overrightarrow{CH}|$ ebenso wie $\overrightarrow{EH}=\overrightarrow{FC}$ und $|\overrightarrow{EH}|=|\overrightarrow{FC}|$ gilt, sind die gegenüberliegenden Seiten jeweils gleich lang und parallel zueinander.

Das Viereck $EFCH$ ist somit ein Parallelogramm.

Winkel bestimmen

In einem Rechteck müssen alle Winkel $90^{\circ}$ betragen, es genügt also, nachzuweisen, dass einer der Innenwinkel kein rechter Winkel ist:

$\begin{array}[t]{rll} \overrightarrow{EF}\circ\overrightarrow{FC}&=&\pmatrix{2\\0\\-1}\circ\pmatrix{0\\3\\-2} & \\[5pt] &=& 2\cdot 0+0\cdot 3+ (-1) \cdot 2 & \\[5pt] &=& -2 \end{array}$

Da im Viereck $EFCH$ folglich nicht alle Innenwinkel auch rechte Winkel sind, handelt es sich hierbei um kein Rechteck.

1.2

Parametergleichung angeben

$J: \overrightarrow{x}=\overrightarrow{OE}+s\cdot \overrightarrow{EF}+t\cdot \overrightarrow{EH}$

Parametergleichung anzeigen

Koordinatengleichung ermitteln

Bestimmen eines Normalenvektors von $J$ durch das Kreuzprodukt der Spannvektoren:

$\begin{array}[t]{rll} \overrightarrow{n_J}&=&\pmatrix{2\\0\\-1}\times \pmatrix{0\\3\\-2} & \\[5pt] &=& \pmatrix{0\cdot (-2)-(-1)\cdot 3\\ (-1) \cdot 0-(-2)\cdot 2\\2\cdot 3-0\cdot 0} & \\[5pt] &=& \pmatrix{3\\4\\6} \end{array}$

Eingesetzt in die allgemeine Koordinatengleichung folgt:

$\begin{array}[t]{rll} J: 3\cdot x+4\cdot y+6\cdot z&=&c \end{array}$

Koordinaten des Punktes $E$ einsetzen:

$\begin{array}[t]{rll} J: 3\cdot 0+4\cdot 0+6\cdot 3&=& c& \\[5pt] 18&=&c \end{array}$

Somit ergibt sich folgende Koordinatenform der Ebene $J$ :

$J: 3x+4y+6z=18$

1.3

Der Neigungswinkel $\varphi$ der beiden Ebenen entspricht dem Winkel zwischen ihren Normalenvektoren. Ein Normalenvektor von $J$ wurde in 1.2 durch $n_J=\pmatrix{3\\4\\6}$ berechnet, ein Normalenvektor der $x$ - $y$ -Ebene ist $n_{xy}=\pmatrix{0\\0\\1}.$

$\begin{array}[t]{rll} \cos (\varphi) &=& \dfrac{|n_J\circ n_{xy}|}{|n_J|\cdot |n_{xy}|}& \\[5pt] \cos (\varphi) &=& \dfrac{\left|\pmatrix{3\\4\\6}\circ \pmatrix{0\\0\\1}\right|}{\left|\pmatrix{3\\4\\6}\right|\cdot \left|\pmatrix{0\\0\\1}\right|}& \quad \scriptsize \mid\; \arccos\\[5pt] \cos (\varphi) &=& \dfrac{6}{\sqrt{61}\cdot 1}& \quad \scriptsize \mid\; \arccos\\[5pt] \varphi&\approx & 39,81 ^{\circ} \end{array}$

Der Neigungswinkel der Ebene $J$ gegenüber der $x$ - $y$ -Ebene beträgt somit ungefähr $39,81 ^{\circ}.$

1.4

$S_y$ ist der Spurpunkt der Ebene mit der $y$ -Achse. Die Koordinaten des Punktes sind $(0 \mid y \mid 0).$ Durch eine Punktprobe würde $y=4,5$ bestimmt werden.

Skizze der Pyramide $AS_xS_yE$

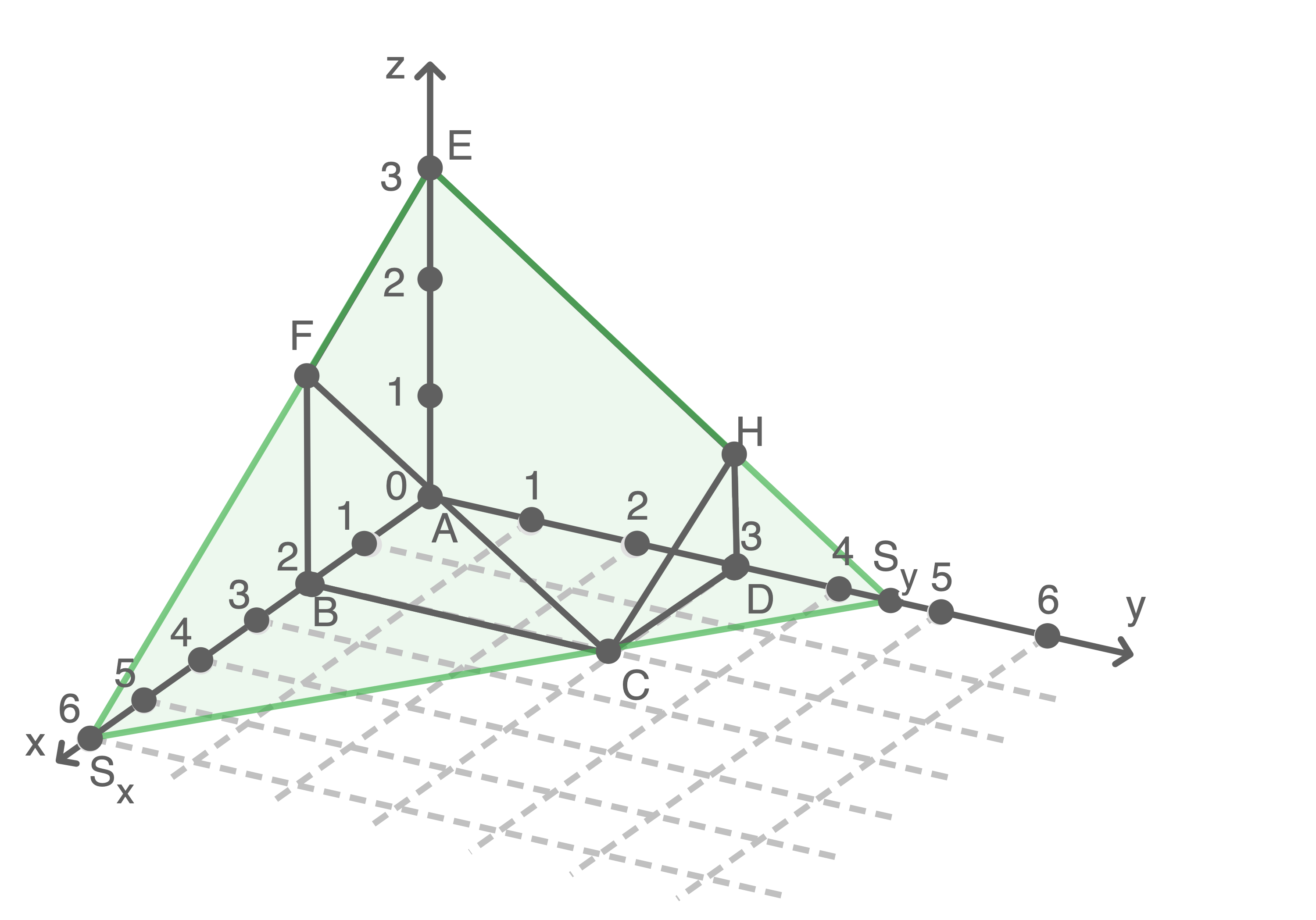
Pyramide kartesisches Koordinatensystem Hessen

1.5

1. Schritt: Volumen der Pyramide berechnen

$\begin{array}[t]{rll} V_P&=& \dfrac{1}{3}\cdot A_{AS_xS_y}\cdot h&\\[5pt] &=& \dfrac{1}{3}\cdot \dfrac{6\cdot 4,5}{2}\cdot 3&\\[5pt] &=& 13,5 \; \text{[VE]} &\\[5pt] \end{array}$

2. Schritt: Volumen der "abschnittenen" Pyramiden berechnen

Pyramide $DCS_yH:$

$\begin{array}[t]{rll} V_1&=& \dfrac{1}{3}\cdot A_{CDS_y}\cdot h& \\[5pt] &=& \dfrac{1}{3}\cdot \dfrac{2\cdot 1,5}{2}\cdot 1& \\[5pt] &=& 0,5 \; \text{[VE]} \end{array}$

Pyramide $BS_xCF:$

$\begin{array}[t]{rll} V_2&=& \dfrac{1}{3}\cdot A_{BS_xC}\cdot h& \\[5pt] &=& \dfrac{1}{3}\cdot \dfrac{4\cdot 3}{2}\cdot 2& \\[5pt] &=& 4 \; \text{[VE]} \end{array}$

3. Schritt: Prozentualen Anteil bestimmen

Der prozentuale Anteil des Körpers $K$ an der Pyramide entspricht also $\dfrac{9}{13,5}=\dfrac{2}{3}=0,6\overline{6}$ und somit etwa $66,6 \,\%.$

1.6

Durch Einsetzen der Komponenten der Geradengleichung in die Koordinatengleichung folgt:

$\begin{array}[t]{rll} 3\cdot (2t-2at)+4\cdot (3at)+6\cdot (3-t-at)&=& 18 &; \\[5pt] 6t -6at +12at+18-6t -6at&=& 18&; \\[5pt] 18&=& 18 \end{array}$

Somit liegen alle Punkte, die auf den Geraden der Schar liegen und somit auch alle Geraden der Schar in der Ebene $J.$

1.7

Wert des Parameters bestimmen

$\begin{array}[t]{rll} \pmatrix{2\\3\\0}&=& \pmatrix{0\\0\\3}+t\cdot \pmatrix{2-2a\\3a\\-1-a} & \\[5pt] \end{array}$

Aus der zweiten Zeile ergibt sich:

$\begin{array}[t]{rll} 3&=&t\cdot 3 \cdot a &\quad \scriptsize \mid\; :3 \quad \scriptsize \mid\; :a\\[5pt] \dfrac{1}{a}&=& t \end{array}$

Durch Einsetzen von $t$ in die erste Zeile folgt:

$\begin{array}[t]{rll} 2&=&\dfrac{1}{a}\cdot (2-2a) & \\[5pt] 2&=&\dfrac{2}{a}-2 &\quad \scriptsize \mid\; +2 \quad \scriptsize \mid\; \cdot a \\[5pt] 4a&=& 2 & \quad \scriptsize \mid\; :4 \\[5pt] a&=& 0,5 \end{array}$

Probe durch Lösen der dritten Zeile :

$\begin{array}[t]{rll} 0&=& 3+\dfrac{1}{a}\cdot (-1-a) &\\[5pt] 0&=& 3+\dfrac{1}{0,5}\cdot (-1-0,5) &\\[5pt] &=& 0 \end{array}$

Somit verläuft die Gerade der Schar mit dem Parameter $a=0,5$ durch den Punkt $C.$

Begründung

Die Gerade der Schar enthält die Strecke $\overline{EC}$ genau dann, wenn sie die Punkte $E$ und $C$ enthält.

Punkt $C$ liegt wie berechnet auf der Geraden mit dem Parameter $a=0,5$ .

Die Gerade verläuft außerdem durch den Punkt $E$ , da der Ortsvektor $\overrightarrow{OE}$ als Stützvektor der Geraden angegeben ist.

Somit enthält die Gerade der Schar auch die gesamte Strecke $\overline{EC}.$

1.8

Geraden, die durch $E$ verlaufen, bestimmen

Der Punkt $E$ ist in allen Geraden der Schar $g_a$ enthalten, da der Vektor $\overrightarrow{OE}$ Stützvektor der Geradengleichungen ist. Zu prüfen ist, für welche $a$ die Punkte $F$ und $H$ in der Geraden der Schar enthalten sind.

1. Schritt: $t$ und $a$ der Geraden, die durch $F$ verlaufen, bestimmen

Rechenweg anzeigen

$\pmatrix{2\\0\\-1}=t\cdot \pmatrix{2-2a\\3a\\-1-a}$

Aus der zweiten Zeile folgt $a=0.$

Einsetzen in die dritte Zeile ergibt:

$\begin{array}[t]{rll} -1&=& t \cdot (-1-0) \\[5pt] -1&=& -t &\quad \scriptsize \mid\;\cdot (-1) \\[5pt] 1&=& t \end{array}$

Probe durch Einsetzen in die erste Zeile ergibt:

$\begin{array}[t]{rll} 2&=& 1 \cdot (2-2\cdot 0) \\[5pt] 2&=& 2 \end{array}$

Es ergibt sich $a=0$ und $t=1.$

2. Schritt: $t$ und $a$ der Geraden, die durch $H$ verlaufen, bestimmen

Rechenweg anzeigen

$\pmatrix{0\\3\\-2} = t\cdot \pmatrix{2-2a\\3a\\-1-a}$

Aus der zweiten Zeile folgt:

$\begin{array}[t]{rll} 3&=& t\cdot 3\cdot a &\quad \scriptsize \mid\;:3t \\[5pt] \dfrac{1}{t}&=& a \end{array}$

Aus der ersten Zeile folgt:

$\begin{array}[t]{rll} 0&=& t\cdot \left(2-2\cdot \dfrac{1}{t} \right) \\[5pt] 0&=& 2t -2 &\quad \scriptsize \mid\;+2 \mid :2 \\[5pt] 1&=&t \end{array}$

Daraus folgt $a=1.$

Probe durch Einsetzen und Lösen der dritten Zeile ergibt:

$\begin{array}[t]{rll} -2 &=& 1\cdot (-1-1)\\[5pt] -2 &=& -2 \end{array}$

Es ergibt sich $a=1$ und $t=1.$

Für alle $0 \leq a \leq 1$ haben die zugehörigen Geraden der Schar mehr als einen Punkt mit dem Parallelogramm $EFCH$ gemeinsam.

1.9

$(\text{I})$ Der Vektor $\pmatrix{-6\\4,5\\0}$ entspricht dem Vektor $\overrightarrow{S_xS_y}.$ Durch das Skalarprodukt mit dem Richtungsvektor der Geradenschar wird der Wert des Parameters $a$ bestimmt, für welchen die zugehörige Gerade orthogonal zur Strecke $\overline{S_xS_y}$ verläuft.

$(\text{II})$ Die zu $\overline{S_xS_y}$ orthogonale Gerade $g$ mit dem berechneten Wert für $a$ wird mit der Geraden, welche die Strecke $\overline{S_xS_y}$ enthält, gleichgesetzt. So kann der Wert von $t$ , für welchen sich die beiden Geraden schneiden, ermittelt werden.

$(\text{III})$ Es wird der Abstand vom Schnittpunkt der beiden Geraden zum Punkt $P(0 \mid 0 \mid 3)$ berechnet.

2.1

Da die Stange senkrecht zur Fläche $EFCH$ und somit zur Ebene $J$ stehen soll, verläuft die Stange entlag $\overrightarrow{n_J}.$

Vektor normieren

$\begin{array}[t]{rll} \overrightarrow{n_{J1}}&=&\dfrac{1}{|\overrightarrow{n_J}|}\cdot \overrightarrow{n_J} & \\[5pt] &=&\dfrac{1}{\sqrt{3^2+4^2+6^2}}\cdot \pmatrix{3\\4\\6} & \\[5pt] &=&\dfrac{1}{\sqrt{61}}\cdot \pmatrix{3\\4\\6} \end{array}$

Koordinaten des Endpunkts $P$ berechnen

$\begin{array}[t]{rll} \overrightarrow{OP}&=& \overrightarrow{OQ}-3\cdot \dfrac{1}{\sqrt{61}}\cdot \pmatrix{3\\4\\6} & \\[5pt] &=& \pmatrix{1,5\\2\\3}-3\cdot \dfrac{1}{\sqrt{61}}\cdot \pmatrix{3\\4\\6} & \\[5pt] &\approx& \pmatrix{1,5\\2\\3}-\pmatrix{1,15\\1,54\\2,3}& \\[5pt] &=& \pmatrix{0,35\\0,46\\0,7} \end{array}$

Die Koordinaten des Endpunkts der Stange, welcher innerhalb des Betonkörpers liegt, sind somit $P(0,35 \mid 0,46 \mid 0,7).$

2.2

$\begin{array}[t]{rll} \overrightarrow{v_S}&=&\overrightarrow{OH}-\overrightarrow{OQ} & \\[5pt] &=&\pmatrix{0\\3\\1}-\pmatrix{1,5\\2\\3} & \\[5pt] &=&\pmatrix{-1,5\\1\\-2} \end{array}$

Der Vektor $\overrightarrow{v_S}=\pmatrix{-1,5\\1\\-2}$ beschreibt die parallel einfallenden Sonnenstrahlen.

2.3

Geradengleichung des Sonnenstrahls, der auf den Punkt $Q$ einfällt:

$\begin{array}[t]{rll} g: \overrightarrow{x}&=&\overrightarrow{OQ}+t\cdot \overrightarrow{v} & \\[5pt] g: \overrightarrow{x}&=&\pmatrix{1,5\\2\\3}+t\cdot \pmatrix{-1,5\\0\\-1}& \\[5pt] \end{array}$

Da der Schattenpunkt $\(Q$ auf dem Boden liegt, muss seine $z$ -Koordinate null sein. Diese Bedingung ist für $t=3$ erfüllt.

Koordinaten von $\(Q$ bestimmen:

$\(\begin{array}[t]{rll} \overrightarrow{OQ$

Der Schattenpunkt $\(Q$ besitzt somit die Koordinaten $\(Q$

Schattenpunkt auf der Kante $EH$ bestimmen

Der gesuchte Punkt der Kante $\overline{EH},$ der im Schatten der Stange liegt, ist der Schnittpunkt der Gerade durch $E$ und $H$ und der Schattenebene.

Die Gerade durch $E$ und $H$ lässt sich wie folgt aufstellen:

$\begin{array}[t]{rll} g_{EH}: \overrightarrow{x}&=& \overrightarrow{OE}+r\cdot \overrightarrow{EH} & \\[5pt] &=&\pmatrix{0\\0\\3} +r\cdot \pmatrix{0\\3\\-2} \end{array}$

Die Schattenebene kann wie folgt aufgestellt werden:

$\begin{array}[t]{rll} E_S&=& \overrightarrow{OQ}+s\cdot \overrightarrow{v}+t\cdot \overrightarrow{n}& \\[5pt] &=&\pmatrix{1,5\\2\\3}+s\cdot \pmatrix{-1,5\\0\\-1}+t\cdot \pmatrix{3\\4\\6} \end{array}$

Durch Gleichsetzen der Gleichung der Schattenebene mit der Geradengleichung von $g_{EH}$ ergibt sich:

$\begin{array}[t]{rll} g_{EH}&=& E_S & \\[5pt] \pmatrix{0\\0\\3} +r\cdot \pmatrix{0\\3\\-2}&=& \pmatrix{1,5\\2\\3}+s\cdot \pmatrix{-1,5\\0\\-1}+t\cdot \pmatrix{3\\4\\6} & \\[5pt] \end{array}$

Mit dem Taschenrechner folgt:

$r=\dfrac{3}{5},s=\dfrac{9}{10}, t=-\dfrac{1}{20}$

Der Schnittpunkt kann nun wie folgt berechnet werden:

$\begin{array}[t]{rll} \overrightarrow{OP}&=& \pmatrix{0\\0\\3} + \dfrac{3}{5}\cdot \pmatrix{0\\3\\-2} & \\[5pt] &=&\pmatrix{0\\1,8\\1,8} \end{array}$

Der Punkt $S\left(0\,\bigg \vert \, 1,8\,\bigg \vert \, 1,8\right)$ auf der Strecke $EH$ liegt folglich im Schatten der Stange.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?