B1 – Analysis

Gegeben ist die Funktionenschar $f_k$ mit $f_k(x)=\left(k^2 \cdot x+k\right) \cdot \mathrm e^{-0,1 k \cdot x}, \; k \in \mathbb{R}^+.$

Im Folgenden soll die Funktionenschar $f_k$ untersucht werden.

1.1

In der folgenden Abbildung sind die Graphen der drei Scharfunktionen $f_2, f_3$ und $f_{3,2}$ dargestellt.

Ordne jedem Graphen den passenden Parameterwert zu.

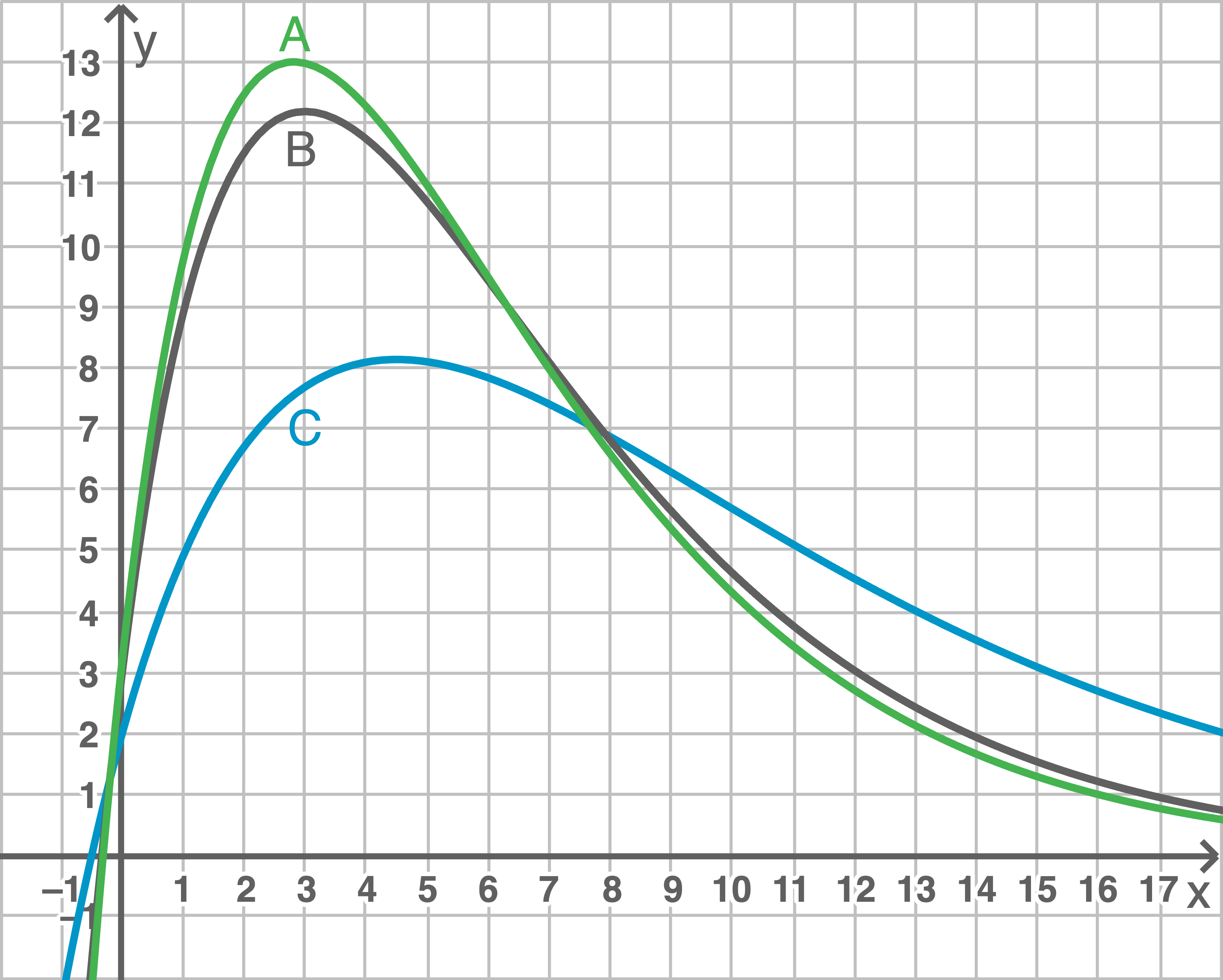
Funktionenschar ABC Hessen Mathe Abi 2024

(2 BE)

1.2

Begründe anhand des Funktionsterms der Funktionenschar, dass sich die Graphen aller Funktionen der Schar für größer werdende $x$ -Werte der $x$ -Achse annähern.

(3 BE)

1.3.1

Gib die Funktionsgleichungen der ersten beiden Ableitungen der Schar $f_k$ an. Diese Gleichungen können ohne weitere Herleitung verwendet werden.

Berechne in Abhängigkeit von $k$ den Wendepunkt jeder Scharkurve.

Die Untersuchung der notwendigen Bedingung ist ausreichend.

$\bigg[$ zur Kontrolle: $W_k \left(\dfrac{19}{k} \,\bigg \vert \, 20k \cdot \mathrm{e}^{-1,9}\right) \bigg]$

(4 BE)

1.3.2

Berechne die Gleichung der Ortskurve der Wendepunkte der Schar $f_k$ und skizziere diese in der Abbildung aus Aufgabe 1.1.

(4 BE)

Die Form bestimmter Vasen soll durch Rotationskörper modelliert werden, die im Intervall $[0;17]$ durch Rotation von Flächen um die $x$ -Achse entstehen.

Dabei soll als äußere Randfunktion der Fläche eine Funktion $g,$ als innere Randfunktion eine geeignete Funktion der Schar $f_k$ verwendet werden.

Im Modell liegt der Boden jeder Vase auf der $y$ -Achse, die Dicke des Bodens soll vernachlässigt werden. Eine Einheit im Koordinatensystem entspricht einem Zentimeter.

2.1

Beschreibe unter Angabe zweier Aspekte, welchen Einfluss der Parameter $k$ der Schar $f_k$ auf die innere Form der zu den Graphen in der Abbildung gehörigen Vasen hat.

(4 BE)

Im Folgenden wird die Vase mit der inneren Randfunktion $f_3$ betrachtet.

Diese Vase hat eine Höhe von $17\,\text{cm}.$

2.2

Um das Füllvolumen der Vase zu berechnen, wird folgender Ansatz gewählt:

$V=\pi \displaystyle\int_{0}^{17}(81x^2+54x+9)\cdot \mathrm e^{-0,6x}\;\mathrm dx$

2.2.1

Leite diesen Ansatz her und gib das Füllvolumen an.

(3 BE)

2.2.2

Bestimme die Füllhöhe der Vase, wenn diese nur zur Hälfte des Füllvolumens mit Wasser gefüllt ist.

(4 BE)

2.3

Für die äußere Randfunktion werden die Funktion $f_{3,2}$ der Funktionenschar und die Funktion $g$ mit $g(x)=(10,24 x+3,2) \cdot \mathrm{e}^{-0,3 x}$ vorgeschlagen.

2.3.1

Beurteile jeweils für die beiden Funktionen $f_{3,2}$ und $g,$ ob sie als äußere Randfunktion geeignet sind.

(4 BE)

2.3.2

Ermittle den Materialverbrauch der Vase in $\,\text{cm}^3$ unter Verwendung der äußeren Randfunktion $g.$

Die Dicke des Bodens der Vase soll dabei vernachlässigt werden.

(3 BE)

2.4

Es wird eine Vase betrachtet, deren Höhe $12\,\text{cm}$ beträgt. Die innere Randfunktion $f_3$ soll so verändert werden, dass ihr Graph ab dem Wendepunkt (Aufgabe 1.3.1) ohne Knick geradlinig weiter verläuft.

Bestimme den Durchmesser der Halsöffnung dieser Vase.

(5 BE)

Es soll eine neue Vase mit einer inneren Randfunktion $r$ entworfen werden. Der innere Rotationskörper der neuen Vase ist im Vergleich zu dem der Vase mit der inneren Randfunktion $f_3$ schlanker (d.h. $r(x)\lt f_3(x)$ ), dafür aber höher (als $17\,\text{cm}$ ).

Der Inhalt der Schnittflächen beider Rotationskörper bei einem Längsschnitt soll gleich bleiben, es gilt also:

$\begin{array}[t]{rll} A_{f_3}&=& 2 \cdot \displaystyle\int_{0}^{17}(9x+3)\cdot \mathrm e^{-0,3x}\;\mathrm dx & \\[5pt] &=& 2 \cdot \displaystyle\int_{0}^{h}r(x)\;\mathrm dx & \\[5pt] &=& A_r \end{array}$

Entscheide begründet, ob das Füllvolumen der neuen Vase kleiner oder größer ist als das Füllvolumen der Vase mit der inneren Randfunktion $f_3$ , oder ob beide Füllvolumen gleich groß sind.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Der Linearfaktor $k^2 \cdot x+k$ im Funktionsterm der Schar beschreibt einen linearen Anstieg mit einer Steigung, die von $k^2$ abhängt. Der Exponentialfaktor $\mathrm{e}^{-0,1 k \cdot x}$ sorgt dafür, dass die Funktion für größere $x$ -Werte abfällt. Dieser Abfall ist umso schneller, je größer $k$ ist, da der Exponent schneller negativ wird.

Somit ergibt sich folgende Zuordnung:

Graph A: $\quad k=3,2$

Graph B: $\quad k=3$

Graph C: $\quad k=2$

1.2

Für große Werte von $x$ dominiert der exponentielle Faktor $\mathrm{e}^{-0,1 k \cdot x}$ den Term $f_k(x).$

Da der Exponentialterm gegen null geht, nähert sich auch $f_k(x)$ für große $x$ -Werte der $x$ -Achse an.

1.3.1

Ableitungen angeben

Mit dem Cas folgt:

$\(f_k$

Wendepunkt jeder Scharkurve bestimmen

1. Schritt: Notwendige Bedingung für Wendestellen anwenden

Rechenweg anzeigen $x= \dfrac{19}{k}$

2. Schritt: $\boldsymbol{y}$ -Koordinate bestimmen

$\begin{array}[t]{rll} f_k\left( \dfrac{19}{k} \right)&=& \left(k^2 \cdot \dfrac{19}{k}+k\right) \cdot \mathrm{e}^{-0,1 k \cdot \frac{19}{k}} & \\[5pt] &=& 20k\cdot \mathrm e^{-1,9} \end{array}$

Die Koordinaten des Wendepunkts jeder Scharkurve sind somit gegeben durch $\left( \dfrac{19}{k} \,\bigg \vert \, 20k\cdot \mathrm e^{-1,9} \right).$

1.3.2

Gleichung der Ortskurve ermitteln

Aus der $x$ -Koordinate des Wendepunkts ergibt sich:

$\begin{array}[t]{rll} x&=& \dfrac{19}{k}&\quad \scriptsize \mid\; \cdot k \quad \scriptsize \mid\;:x \\[5pt] k&=& \dfrac{19}{x} \end{array}$

Die $y$ -Koordinate der Wendepunkte ist in Abhängigkeit von $k$ gegeben durch $y=20k\cdot \mathrm e^{-1,9}.$

Einsetzen von $k=\dfrac{19}{x}$ liefert:

$\begin{array}[t]{rll} y&=& 20\cdot \dfrac{19}{x}\cdot \mathrm e^{-1,9} & \\[5pt] &=& \dfrac{380}{x}\cdot \mathrm e^{-1,9} \end{array}$

Die Gleichung der Ortskurve der Wendepunkte lautet also $y = \dfrac{380}{x} \cdot \mathrm{e}^{-1,9}$ .

Ortskurve skizzieren

Mit dem CAS kann die Ortskurve graphisch dargestellt werden. Der Graph muss durch die Wendepunkte der bereits abgebildeten Graphen verlaufen.

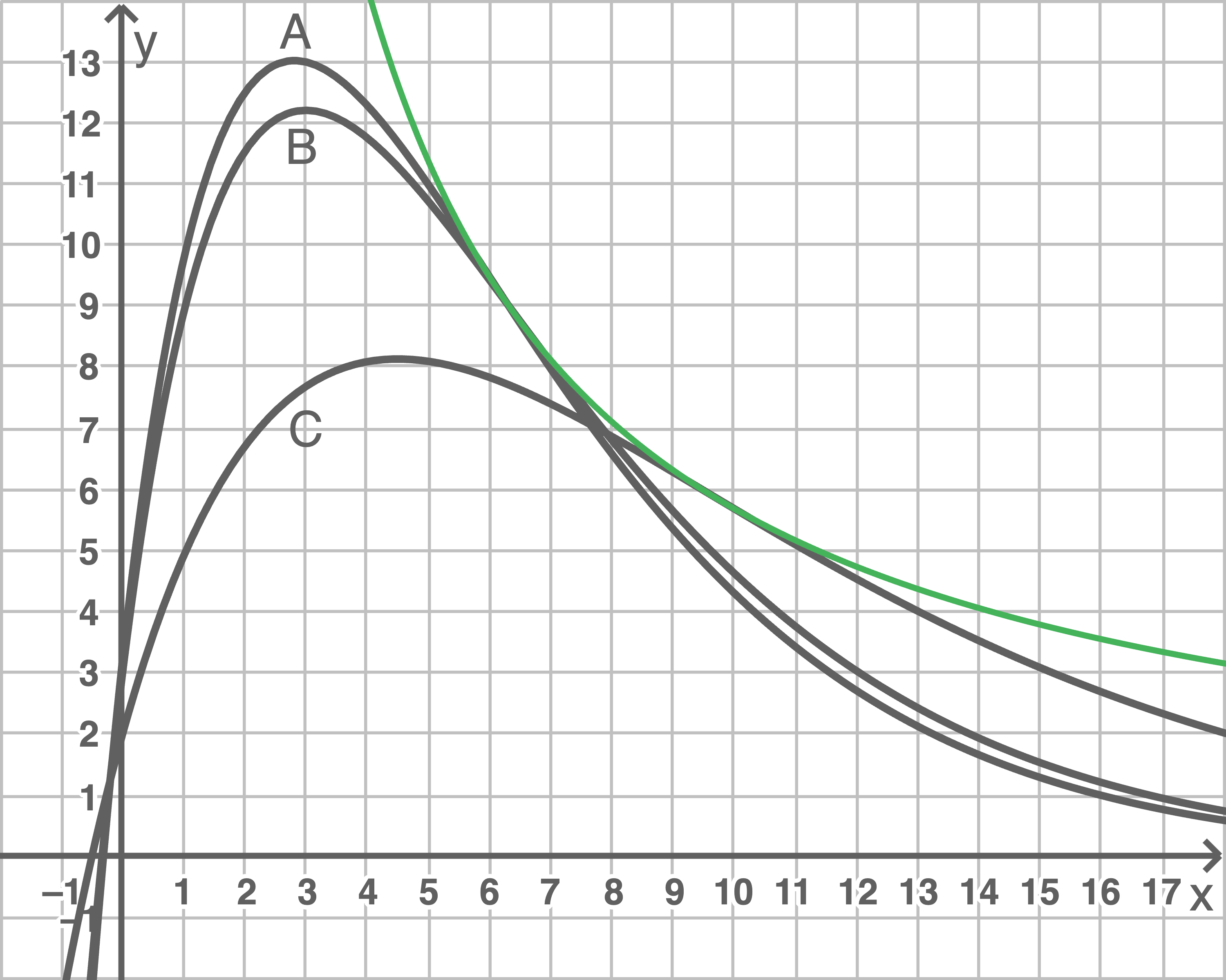
2.1

Der Parameter $k$ beeinflusst die Form der Vase wie folgt:

Umso größer der Wert von $k,$ desto größer ist die Wölbung des unteren inneren Teils der Vase und somit die Breite der inneren Form.
Umso größer der Wert von $k,$ desto schmaler ist der obere innere Teil der Vase und somit die Öffnung der Vase.

2.2.1

Ansatz herleiten

Der Ansatz zur Berechnung des Volumens der Vase ergibt sich durch das Rotieren der Funktion $f_3$ um die $x$ -Achse.

Mit $f_3(x)=(9x + 3) \cdot \mathrm{e}^{-0,3x}$ gilt für das Rotationsvolumen:

$V= \pi\cdot \displaystyle\int_{0}^{17}f_3(x)^2 \;\mathrm dx$

Vollständige Herleitung anzeigen

Füllvolumen angeben

Mit dem CAS ergibt sich:

$\begin{array}[t]{rll} V&=& \pi\cdot \displaystyle\int_{0}^{17} (81x^2 + 54x + 9) \cdot \mathrm{e}^{-0,6x} \;\mathrm dx & \\[5pt] &\approx& 2868,8 \, [\,\text{cm}^3] \end{array}$

Das Füllvolumen der Vase beträgt somit etwa $2868,8 \,\text{cm}^3,$ also ca. $2,9$ Liter.

2.2.2

Die Hälfte des Füllvolumens beträgt $2868,8 \,\text{cm}^3 :2= 1434,4 \,\text{cm}^3.$

Beschreibt $h$ die Füllhöhe der Vase, so muss gelten:

$\pi\cdot \displaystyle\int_{0}^{h} (81x^2 + 54x + 9) \cdot \mathrm{e}^{-0,6x} \;\mathrm dx = 1434,4$

Mit dem solve-Befehl des CAS ergibt sich:

$h\approx 4,13 [\,\text{cm}]$

2.3.1

Als äußere Randfunktion sind alle Funktionen zugelassen, die im Intervall $[0; 17]$ stets oberhalb der inneren Randfunktion $f_3$ verlaufen.

Aus der Abbildung in Aufgabe 1.1 kann abgelesen werden, dass sich die Graphen der Funktionen $f_3$ und $f_{3,2}$ in diesem Intervall schneiden. Die Funktion $f_{3,2}$ ist somit nicht als äußere Randfunktion geeignet.

Für die Funktion $g$ gilt:

$g(x)= f_3(x)$

Vollständige Gleichung anzeigen

Das CAS liefert, dass diese Gleichung keine Lösung im Intervall $[0; 17]$ besitzt.

Darstellen der beiden Graphen im CAS liefert außerdem, dass der Graph von $g$ im betrachteten Intervall oberhalb des Graphen von $f_3$ verläuft.

Die Funktion $g$ ist folglich als äußere Randfunktion geeignet.

2.3.2

Der Materialverbrauch der Vase ergibt sich als Differenz der Volumina, die sich durch die äußere und innere Funktion ergeben:

Mit dem CAS ergibt sich also:

$V_{\text{Material}} \approx 799,5 \; [\,\text{cm}^3]$

Rechnung anzeigen

Der Materialverbrauch der Vase beträgt somit etwa $799,5 \,\text{cm}^3.$

2.4

Aus der Aufgabe 1.3.1 sind die Koordinaten der Wendepunkte der Schar in Abhängigkeit von $k$ bekannt. Für $f_3$ folgt also:

$W_3\left(\dfrac{19}{3}\,\bigg \vert \, 60\cdot \mathrm e^{-1,9}\right)$

Ab dem Wendepunkt verläuft die innere Randfunktion linear mit der Steigung $\(m=f_3$

Mit dem CAS ergibt sich die erste Ableitung von $f_3$ zu:

$\(f_3$

Es gilt also:

$\(\begin{array}[t]{rll} m&=& f_3$

Einsetzen der Steigung $m$ sowie der Koordinaten des Wendepunkts in die allgemeine Tangentengleichung liefert:

$\begin{array}[t]{rll} t: \quad \quad \quad y&=& m\cdot x+c& \\[5pt] 60\cdot \mathrm e^{-1,9}&=& -1,35\cdot \dfrac{19}{3}+c& \\[5pt] 60\cdot \mathrm e^{-1,9}&=& -8,55+c&\quad \scriptsize \mid\; +8,55 \\[5pt] 17,52&\approx& c \end{array}$

Ab dem Wendepunkt verläuft die Vase somit entlang der Tangente $t: \; y=-1,35\cdot x+17,52.$

Da die Vase $12\,\text{cm}$ hoch sein soll, entspricht der Radius ihrer Halsöffnung der $y$ -Koordinate an der Stelle $x=12:$

$\begin{array}[t]{rll} y&=& -1,35\cdot 12+17,52& \\[5pt] &=& 1,32 \end{array}$

Der Durchmesser der Halsöffnung der Vase ist somit gegeben durch $2\cdot 1,32 \; \text{cm} = 2,64 \; \text{cm}.$

Das Füllvolumen der Vase lässt sich wie in Aufgabe 2.2.1 hergeleitet mit folgender Formel berechnen:

$V=\pi \cdot \displaystyle\int_{0}^{17}f_3(x)^2 \;\mathrm dx$

Analog gilt für das Füllvolumen der neuen Vase:

$V_\text{neu}=\pi \cdot \displaystyle\int_{0}^{h}r(x)^2 \;\mathrm dx$

Die Höhe $h$ der neuen Vase und somit die obere Integralsgrenze ist genau so gewählt, dass trotz $r(x) \lt f_3(x)$ Gleichheit der Integrale zur Bestimmung der Schnittflächen gilt.

Wegen $r(x) \lt f_3(x)$ gilt auch $r(x)^2\lt f_3(x)^2.$

Durch das Quadrieren der Randfunktionen zur Bestimmung der Füllmenge wird jedoch auch die Differenz der Integrale über die beiden Funktionen proportional zum Quadrat der Randfunktion größer, während die obere Integralsgrenze $h$ konstant bleibt.

Das Füllvolumen der neuen Vase wird folglich geringer sein.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?