A2 - Analysis

Auf einem Abenteuerspielplatz befindet sich eine Balancierbrücke für Kinder. Zur Absturzsicherung sind auf beiden Seiten der Brücke jeweils sechs vertikal zum Boden verlaufende Stützpfeiler angebracht. Auf beiden Seiten der Brücke verbindet jeweils ein Handlaufseil die oberen Enden der Stützpfeiler. Die Abbildung in Material 1 zeigt das Profil der Brücke mit den vorderen $6$ Stützpfeilern und den Aufhängepunkten $A,$ $B,$ $C,$ $D,$ $E$ und $F$ des Handlaufseils. Eine Einheit entspricht dabei einem Meter.
Die $x$ -Achse verläuft im horizontalen, ebenen Boden des Spielplatzes. Der Verlauf der Brücke und der Handlaufseile ist symmetrisch zur Brückenmitte. Die vertikalen Entfernungen von den Aufhängepunkten zur Brücke sind (auf Millimeter gerundet) jeweils gleich. Der Verlauf des Handlaufseils von Punkt $A$ bis Punkt $B$ kann durch den Graphen der Funktion $f_1$ mit

$f_1(x) = ...$

Vollständige Lösung anzeigen

beschrieben werden.

1.1

Berechne die Höhe der Aufhängepunkte $A$ und $B$ über dem Spielplatzboden und zeige, dass beide Aufhängepunkte eine vertikale Entfernung von $90\,\text{cm}$ zur Brücke haben.

(3 BE)

1.2

Die Kurve, die in Material 1 von Punkt $B$ bis Punkt $C$ verläuft, ist deckungsgleich zu derjenigen, die von Punkt $A$ bis Punkt $B$ verläuft. Sie kann durch den Graphen einer Funktion $f_2$ beschrieben werden.

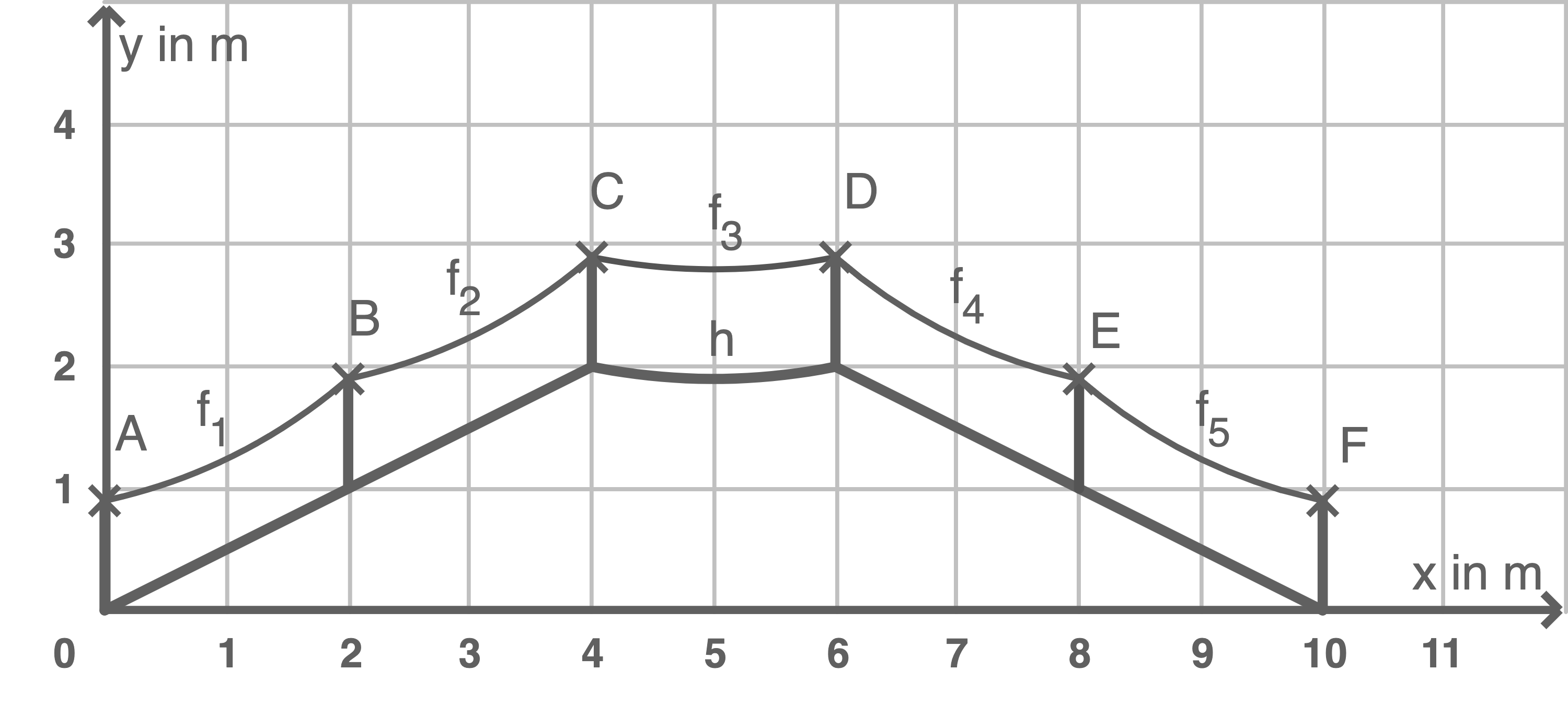
Material 1

1.2.1

Berechne, unter welchem Winkel die beiden Seilenden im Aufhängepunkt $B$ aneinanderstoßen.

(6 BE)

1.2.2

Bestimme den Term der Funktion $f_2.$

(2 BE)

1.3

Deute die untenstehenden Rechenschritte (1) bis (4) im Sachzusammenhang. Die vier als Schritt (2) notierten Zeilen können zusammenhängend gedeutet werden.

(1)

Rechenschritt anzeigen

(2)

Rechenschritt anzeigen

$d‘(x)=0$ $\Rightarrow x\approx 1,064$

$d‘‘(1,064) \gt 0$

$d(1,064)\approx 0,741$

(3)

$y=0,5x$ $\Rightarrow \arctan(0,5) \approx 26,565^{\circ}$

(4)

$d^{*}$ $= 0,741\cdot \cos(26,565^{\circ})$ $\approx 0,663$

(6 BE)

Betrachtet wird die Funktionenschar $g_{a,c}$ mit $g_{a,c}(x) = \frac{a}{2c}\left(\mathrm e^{c\cdot x}+\mathrm e^{-c\cdot x} \right),$ wobei $a \gt 0$ und $c \gt 0$ gelten soll.

2.1

Zeige, dass die Graphen aller Funktionen der Schar $g_{a,c}$ achsensymmetrisch zur $y$ -Achse sind und an der Stelle $x = 0$ einen Tiefpunkt besitzen.

(7 BE)

2.2

Zwischen den Punkten $C$ und $D$ hängt das Seil in der Mitte $10\,\text{cm}$ durch.
Zeige anhand der drei vorgegebenen Punkte, dass sich der Verlauf des Handlaufseils von Punkt $C$ bis Punkt $D$ annähernd durch den im Material 1 dargestellten Graphen der Funktion $f_3$ mit

$f_3(x)=...$

Vollständige Lösung anzeigen

beschreiben lässt.
Bestätige, dass es sich beim Graphen der Funktion $f_3$ um einen in Richtung der positiven $x$ -Achse verschobenen Graphen einer Funktion der Schar $g_{a,c}$ handelt, und gib die zugehörigen Werte der Parameter $a$ und $c$ an.

(6 BE)

2.3

Bestimme unter Verwendung von Material 2 die Gesamtlänge der verwendeten Handlaufseile der Brücke.

Material 2

Der im Intervall $[a;b]$ liegende Abschnitt des Graphen einer differenzierbaren Funktion $f$ hat die Bogenlänge $s= \displaystyle\int_{a}^{b}\sqrt{1+\left(f‘(x)\right)^2}\;\mathrm dx.$

(5 BE)

2.4

Der mittlere Teil der Brücke hat im Bereich von Punkt $C$ bis Punkt $D$ zu dem darüber hängenden Handlaufseil überall die gleiche vertikale Entfernung. Begründe, dass der Verlauf des mittleren Teils der Brücke durch den Graphen der Funktion $h$ mit

$h(x)=...$

Vollständige Lösung anzeigen

beschrieben werden kann.

(1 BE)

Zur größeren Sicherheit für die Kinder sollen die freien Flächen zwischen den Handlaufseilen und der Brücke mit Netzen bespannt werden. Bestimme den Flächeninhalt der gesamten Fläche, die mit Netzen zu bespannen ist.

(4 BE)

1.1

Höhe der Aufhängepunkte bestimmen

Die Höhe des Aufhängepunkts $A$ über dem Spielplatzboden wird durch $f_1(0)$ beschrieben, die Höhe von $B$ durch $f_1(2):$

Rechenweg anzeigen

$f_1(0)=0,9$

Rechenweg anzeigen

$f_1(2)\approx 1,90$

Der Aufhängepunkt $A$ befindet sich folglich in einer Höhe von $90\,\text{cm}$ über dem Spielplatzboden, der Aufhängepunkt $B$ befindet sich in einer Höhe von ca. $1,90\,\text{m}$ über dem Spielplatzboden.

Vertikale Entfernung prüfen

Die Brücke beginnt auf dem Spielplatzboden. Der Punkt auf der Brücke, der direkt vertikal unter dem Aufhängepunkt $A$ verläuft, ist also der Koordinatenursprung $(0\mid0).$ Der vertikale Abstand von $A$ zum Koordinatenursprung entspricht der $y$ -Koordinate von $A$ und beträgt demnach $90\,\text{cm}.$

Da der vertikale Abstand der Aufhängepunkte zur Brücke laut Aufgabentext jeweils bis auf Millimeter genau identisch ist, ist auch der vertikale Abstand vom Aufhängepunkt $B$ zur Brücke ca. $90\,\text{cm}.$

1.2.1

Gesucht ist der Schnittwinkel der beiden Kurven $f_1$ und $f_2$ an der Stelle $x=2.$

Da die Kurve $f_2$ deckungsgleich ist zur Kurve $f_1,$ entspricht ihre Steigung an der Stelle $x=2$ der Steigung des Graphen von $f_1$ an der Stelle $x=0.$

Erste Ableitung bilden:

Ableitung anzeigen

Steigungen am Punkt $A$ und $B$ berechnen:

Rechenweg anzeigen

$\( f_1$

Rechenweg anzeigen

$\( f_1$

Einsetzen in die Formel für den Schnittwinkel zweier Funktionen liefert:

Rechenweg anzeigen

$\alpha \approx 28,4^{\circ}$

Im Aufhängepunkt $B$ stoßen die beiden Seile folglich in einem Winkel von ca. $28,4^{\circ}$ aufeinander.

1.2.2

Der Graph von $f_2$ entsteht durch Verschiebung des Graphen von $f_1$ entlang der $x$ -Achse und entlang der $y$ -Achse. Die Verschiebung entlang der $x$ -Achse muss zwei Einheiten in positive Richtung betragen:

$f_2(x)= f_1(x-2)+c$

Nun muss $c$ so bestimmt werden, dass der Funktionswert von $f_2$ an der Stelle $x=2$ dem von $f_1$ entspricht:

$\begin{array}[t]{rll} f_2(2)&=& f_1(2) \\[5pt] f_1(2-2)+c&=& f_1(2) \\[5pt] f_1(0) +c &=& f_1(2) \\[5pt] 0,90 + c&\approx& 1,90 &\quad \scriptsize \mid\;-0,90 \\[5pt] c&\approx& 1,00 \end{array}$

Der Term der Funktion $f_2$ lautet somit:

$f_2(x)=...$

Lösung anzeigen

1.3

(1)

Der Term $0,6675 \cdot \mathrm e^{0,5x} + 0,2325 \cdot \mathrm e^{-0,5x}$ beschreibt den Graphen von $f_1,$ also den Verlauf des Handlaufseils zwischen den Aufhängepunkten $A$ und $B.$ Der Term $0,5x$ beschreibt den Graphen einer Geraden. Diese beschreibt den Verlauf des linken Brückenteils.

In der ersten Zeile wird die Differenzenfunktion $d$ dieser beiden Funktionen gebildet. Diese beschreibt also den vertikalen Abstand der beiden Graphen und im Sachzusammenhang somit den vertikalen Abstand zwischen Handlaufseil und Brücke.

(2)

Es wird die erste Ableitung der Abstandsfunktion $d$ gebildet und mit Null gleichgesetzt. Dies entspricht der Anwendung des notwendigen Kriteriums für Extremstellen von $d.$
Das Ergebnis wird in die zweite Ableitungsfunktion $d‘‘$ eingesetzt. Dieser Funktionswert ist positiv. Aufgrund des hinreichenden Kriteriums für Extremstellen handelt es sich bei $x\approx 1,064$ also um ein lokales Minimum von $d.$
Der zugehörige Funktionswert von $d$ wird mit $d(1,064)\approx 0,741$ berechnet.
Der kleinste vertikale Abstand zwischen dem Handlaufseil und der Brücke zwischen den Aufhängungspunkten $A$ und $B$ beträgt also ca. $74,1\,\text{cm}.$

(3)

In der dritten Zeile wird der Steigungswinkel der Gerade berechnet, die den Verlauf des linken Brückenteils beschreibt. Diese steigt in einem Winkel von ca. $26,565^{\circ}$ an.

(4)

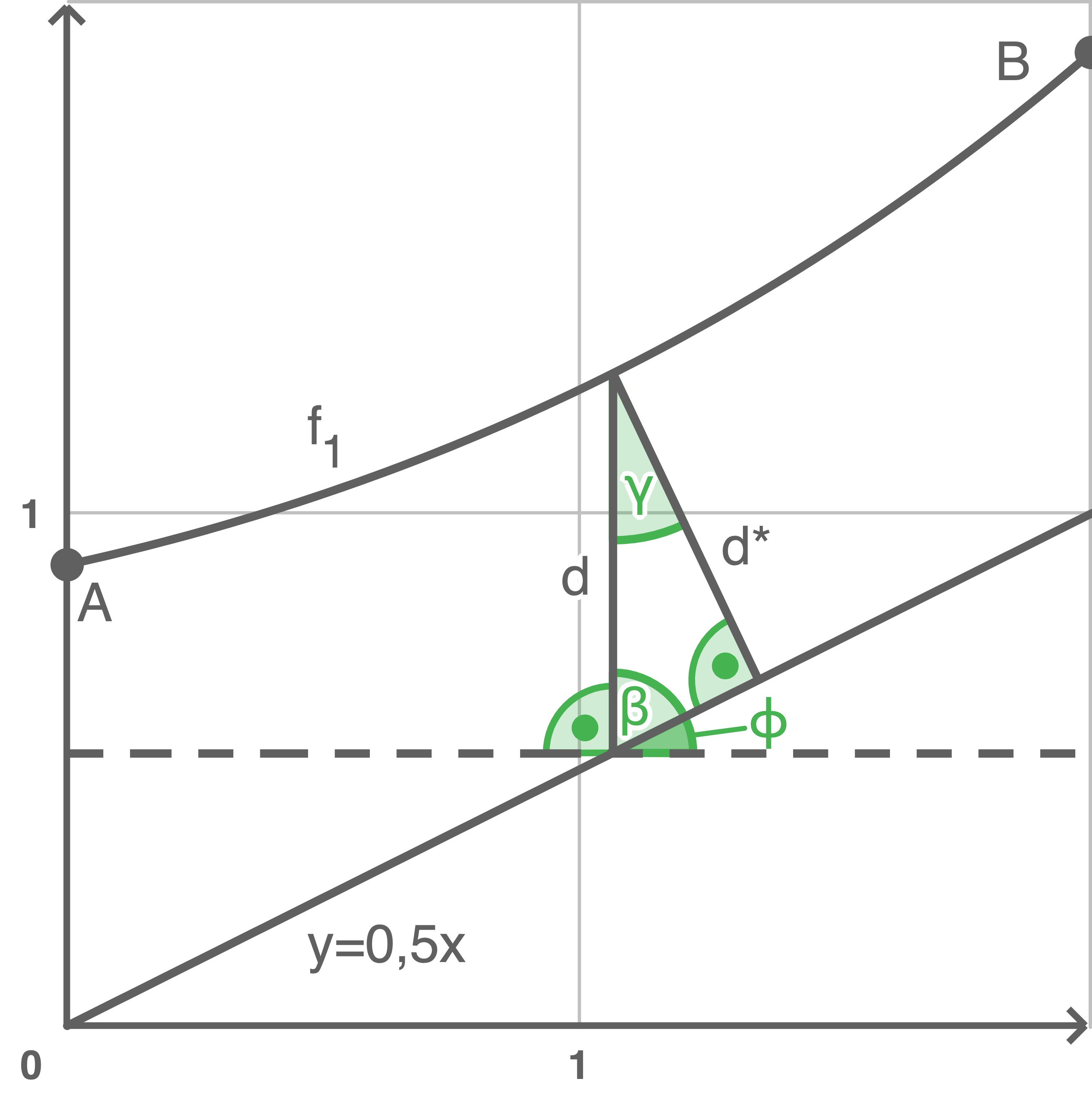
In der nebenstehenden Skizze bezeichnet der Winkel $\phi$ den oben beschriebenen Steigungswinkel der Geraden $y=0,5x.$ Dieser bildet gemeinsam mit dem Winkel $\beta$ einen rechten Winkel, wodurch die Beziehung $\beta = 90^{\circ} -\phi$ gilt.

Zudem besitzt das eingezeichnete Dreieck einen rechten Winkel, den die Strecke $d^*$ und die Gerade $y=0,5x$ zusammen bilden. Für den dritten Winkel des Dreiecks gilt dann aufgrund der Winkelsumme:

$\begin{array}[t]{rll} \gamma &=& 180^{\circ} - 90^{\circ} - \beta & \\[5pt] &=& 90^{\circ}-(90^{\circ}-\phi)& \\[5pt] &=& \phi \end{array}$

Hilfsskizze Haengebruecke Hessen Abi CAS

Dieser entspricht also wiederum dem Steigungswinkel $\phi$ der Geraden. Die Strecke $d^*$ bildet die Ankathete zu $\gamma$ und $d$ die Hypotenuse des rechtwinkligen Dreiecks. In der vierten Zeile wurde daher nun die Cosinus-Beziehung ausgenutzt um $d^*$ mithilfe des Winkels $\phi$ beziehungsweise $\gamma$ und der Strecke $d$ zu berechnen.

Der Skizze kann man nun entnehmen, dass $d*$ dem kürzesten Abstand zwischen der Brücke und dem Punkt, in dem das Handlaufseil den kürzesten vertikalen Abstand zur Brücke besitzt, entspricht.

In dem Punkt, in dem das Handlaufseil den kürzesten vertikalen Abstand zur Brücke besitzt, ist das Handlaufseil also ca. $66,3\,\text{cm}$ von der Brücke entfernt.

2.1

Symmetrie zeigen

$\begin{array}[t]{rll} g_{a,c}(-x)&=& \frac{a}{2c}\left(\mathrm e^{c\cdot (-x)} +\mathrm e^{-c\cdot (-x)} \right) \\[5pt] &=& \frac{a}{2c}\left(\mathrm e^{-c\cdot x} +\mathrm e^{c\cdot x} \right) \\[5pt] &=& \frac{a}{2c}\left(\mathrm e^{c\cdot x} +\mathrm e^{-c\cdot x}\right) \\[5pt] &=& g_{a,c}(x) \\[5pt] \end{array}$

Es gilt also für alle $a\gt 0, \; c\gt 0:$

$g_{a,c}(-x)=g_{a,c}(x)$

Die Graphen von $g_{a,c}$ sind somit symmetrisch zur $y$ -Achse.

Tiefpunkt nachweisen

Ableitungsfunktionen bestimmen:

$\begin{array}[t]{rll} g_{a,c}(x)&=& \frac{a}{2c}\left(\mathrm e^{c\cdot x} +\mathrm e^{-c\cdot x}\right) \\[10pt] \end{array}$

$\(\begin{array}[t]{rll} g_{a,c}$

1. Schritt: Notwendiges Kriterium anwenden

$\(\begin{array}[t]{rll} g_{a,c}$

2. Schritt: Hinreichendes Kriterium überprüfen

$\(\begin{array}[t]{rll} g_{a,c}$

Da $a\gt 0$ und $c\gt 0$ vorgegeben sind folgt $\(g_{a,c}$

Die Graphen von $g_{a,c}$ besitzen also jeweils einen Tiefpunkt an der Stelle $x=0.$

2.2

1. Schritt: Verlauf des Graphen zeigen

$\begin{array}[t]{rll} f_2(4)&=& f_1(4-2)+1 \\[5pt] &=& f_1(2)+1\\[5pt] &=& 1,90 +1 \\[5pt] &=& 2,90 \end{array}$

Da die Brücke sowie auch die Handlaufseile symmetrisch zur Brückenmitte verlaufen, folgen die Koordinaten der Punkte $C$ und $D$ mit $C(4\mid 2,90)$ und $D(6\mid 2,90).$

Die Koordinaten des Durchhängepunkts lauten entsprechend $M(5\mid 2,80).$

2. Schritt: Koordinaten der Punkte überprüfen

Rechenweg anzeigen

$f_3(4)\approx 2,90$

Rechenweg anzeigen

$f_3(5)= 2,8$

Rechenweg anzeigen

$f_3(6)\approx 2,90$

Auf zwei Nachkommastellen gerundet stimmen die Funktionswerte von $f_3$ also mit den Koordinaten der Punkte $C,\; D$ und $M$ überein. Der Verlauf des Handlaufseils zwischen den Punkten $C$ und $D$ lässt sich also annähernd durch den Graphen von $f_3$ darstellen.

Zugehörigkeit zur Schar bestätigen

Der Term $(x-5)$ in den Exponenten der Funktion $f_3$ führt zu einer Verschiebung des Graphen um $5$ Einheiten entlang der $x$ -Achse in positiver Richtung.

Durch einen Koeffizientenvergleich folgt, dass $c= 0,26647$ sein muss.

Mithilfe des Faktors vor der Klammer lässt sich nun $a$ bestimmen:

Rechenweg anzeigen

$a=0,746116$

Die Funktion $g_{0,746116;0,26647}$ ist also gegeben durch:

$g_{0,746116;0,26647}(x) =...$

Funktion anzeigen

Somit ist sie für $a= 0,746116$ und $c=0,26647$ Teil der Schar $g_{a,c}.$

Durch eine Verschiebung des zugehörigen Graphen um $5$ Einheiten entlang der $x$ -Achse in positive Richtung entsteht der Graph von $f_3.$

2.3

Da die Kurve zwischen den Punkten $B$ und $C$ deckungsgleich mit der zwischen $A$ und $B$ ist, und die Brücke achsensymmetrisch zur Brückenmitte ist, genügt es die Bogenlänge von $f_1$ zwischen $A$ und $B$ und die Bogenlänge von $f_3$ zwischen $C$ und $D$ zu berechnen:

$s_{f_1}=...$

Rechnung anzeigen

Mit dem CAS kann das Integral berechnet werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

Es folgt: $s_{f_1} \approx 2,260$

Ebenso kann die Bogenlänge von $f_3$ bestimmt werden.

Hierfür muss zuerst die Ableitung gebildet werden:

$\( f_3$

Ableitung anzeigen

Mit dem CAS folgt:

Rechenweg anzeigen

$s_{f_3} \approx 2,013$

Die Gesamtlänge lässt sich nun wie folt berechnen:

$\begin{array}[t]{rll} l&=&4\cdot s_{f_1} + s_{f_3} & \\[5pt] &\approx& 4\cdot 2,260 + 2,013 & \\[5pt] &=& 11,053 \end{array}$

Das gesamte Handlaufseil einer Seite ist somit etwa $11,053\,\text{m}$ lang. Für beide Seiten werden also insgesamt $22,106\,\text{m}$ Handlaufseil verwendet.

2.4

Da die Brücke an jeder Stelle den gleichen vertikalen Abstand zum Handlaufseil haben soll, muss dies auch für die beiden zugehörigen Graphen gelten. Der Graph von $h$ entsteht daher durch Verschiebung des Graphen von $f_3$ entlang der $y$ -Achse in negative Richtung.

Laut Aufgabenstellung sind die vertikalen Entfernungen der Aufhängepunkte $A$ bis $F$ zur Brücke jeweils identisch. Diese vertikale Entfernung beträgt laut Aufgabe 1.1 $90\,\text{cm}$ und gilt demnach auch für $C$ und $D,$ sowie den Verlauf des Handlaufseils dazwischen.

Der mittlere Brückenteil verläuft also $90\,\text{cm}$ unter dem Handlaufseil zwischen $C$ und $D,$ sodass der Graph von $h$ durch Verschiebung des Graphen von $f_3$ um $0,9$ Einheiten in negative Richtung entlang der $y$ -Achse entsteht.

Es gilt also:

$h(x)=...$

Rechnung anzeigen

Aufgrund der Symmetrie der Brücke kann der Flächeninhalt in zwei Teilrechnungen aufgeteilt werden:

Der Flächeninhalt $A_1$ zwischen dem Graphen von $f_1$ und der Geraden zu $y = 0,5x$ im Intervall $[0;2]$ mithilfe eines Integrals berechnet werden.

Der Flächeninhalt zwischen den Graphen von $f_3$ und $h$ im Intervall $[4;6]$ kann aufgrund des identischen vertikalen Abstandes zwischen den Graphen wie der Flächeninhalt eines Rechtecks mit den Seitenlängen $a= 2$ und $b\approx 0,90$ ermittelt werden:
$A_2 \approx 2\,\text{m}\cdot 0,90\,\text{m} = 1,80\,\text{m}^2.$