C1 - Lineare Algebra/ Analytische Geometrie
Die „Puerta de Europa“ in Madrid besteht aus zwei einander zugeneigten Türmen (Material 1), die jeweils die Form eines Spats aufweisen. Ein Spat ist ein Körper, dessen Oberfläche aus sechs Parallelogrammen besteht, wobei jeweils gegenüberliegende Flächen kongruent und parallel zueinander sind.
Im Modell liegen die Bodenflächen beider Türme in der -
- -Ebene, die den Erdboden beschreibt.
-Ebene, die den Erdboden beschreibt.
Die Dachflächen liegen in einer Ebene, die parallel zur -
- -Ebene verläuft, die Nord- und Südwände liegen jeweils in einer Ebene, die parallel zur
-Ebene verläuft, die Nord- und Südwände liegen jeweils in einer Ebene, die parallel zur  -
- -Ebene verläuft. Die (positive)
-Ebene verläuft. Die (positive)  -Achse zeigt in Richtung Süden, die (positive)
-Achse zeigt in Richtung Süden, die (positive)  -Achse in Richtung Osten.
Die Türme haben jeweils eine Höhe von
-Achse in Richtung Osten.
Die Türme haben jeweils eine Höhe von  . Der Ostturm hat unter anderem die Eckpunkte
. Der Ostturm hat unter anderem die Eckpunkte 

 und
und 
Eine Längeneinheit entspricht dabei


Im Modell liegen die Bodenflächen beider Türme in der
Die Dachflächen liegen in einer Ebene, die parallel zur
Eine Längeneinheit entspricht dabei


Material 1: Bilder der Puerta de Europa
1.1
Die Eckpunkte  und
und  begrenzen gemeinsam mit einem Punkt
begrenzen gemeinsam mit einem Punkt  die quadratische Bodenfläche des Ostturms. Gib den Eckpunkt
die quadratische Bodenfläche des Ostturms. Gib den Eckpunkt  an und bestimme den Flächeninhalt der Bodenfläche des Ostturms.
an und bestimme den Flächeninhalt der Bodenfläche des Ostturms.
(4 BE)
1.2
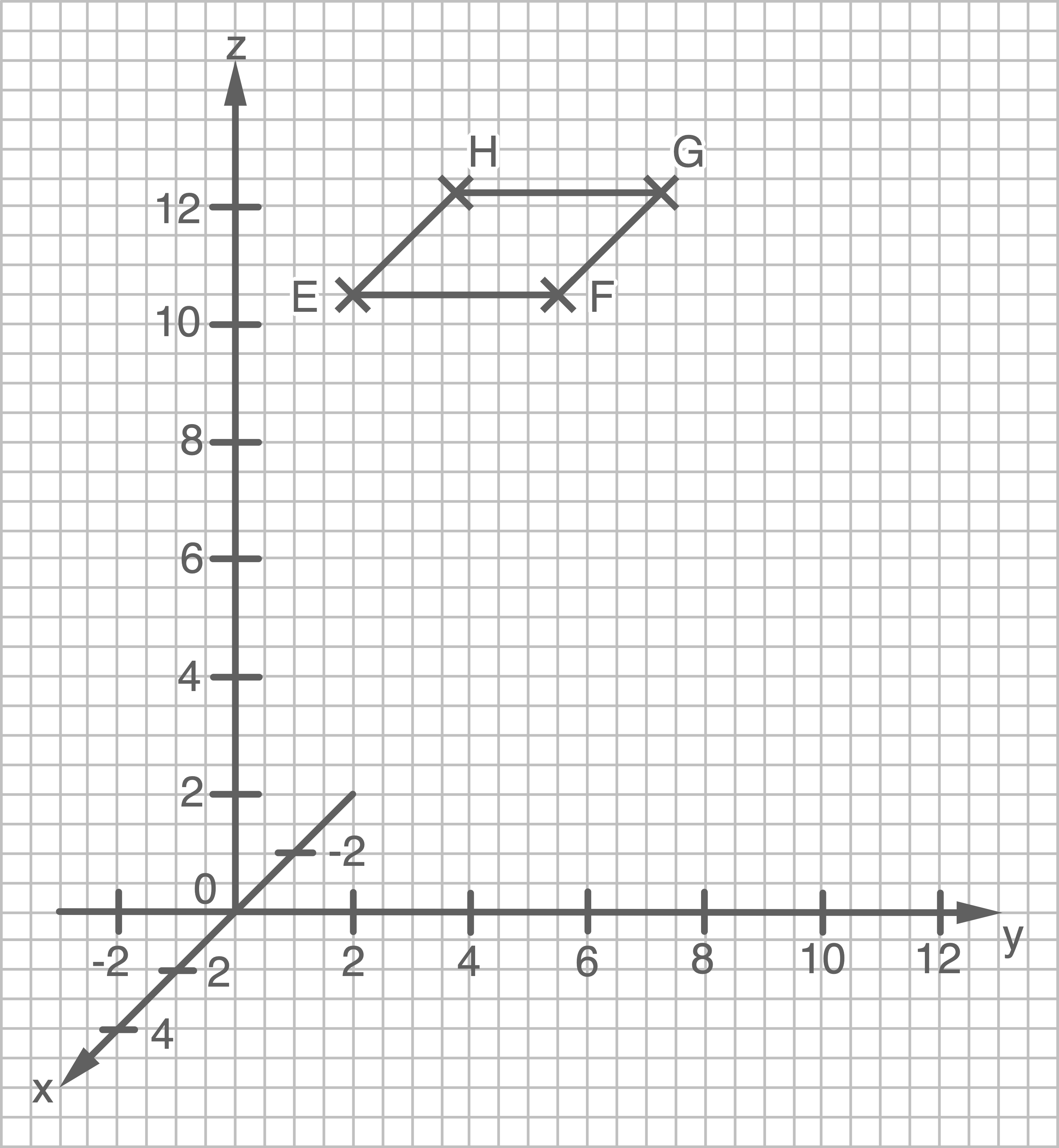
Im Koordinatensystem in Material 2 ist die Dachfläche des Ostturms eingezeichnet.
Gib die Koordinaten der fehlenden Eckpunkte und
und  des Ostturms an.
des Ostturms an.
Zeichne den gesamten Ostturm in das Koordinatensystem ein.
Gib die Koordinaten der fehlenden Eckpunkte
Zeichne den gesamten Ostturm in das Koordinatensystem ein.
(7 BE)

Material 2: Dachfläche des Ostturms
1.3
Zeige, dass der Neigungswinkel des Ostturms (in westlicher Richtung) gegenüber der Vertikalen etwa  beträgt.
beträgt.
(3 BE)
2
Im Modell entspricht der Westturm einer Spiegelung des Ostturms an der  -
- -Ebene.
-Ebene.
2.1
Gib eine Spiegelmatrix  an, mit deren Hilfe man für einen beliebigen Punkt
an, mit deren Hilfe man für einen beliebigen Punkt  des Ostturms mit Hilfe der Gleichung
des Ostturms mit Hilfe der Gleichung  den entsprechenden (gespiegelten) Punkt des Westturms ermitteln kann.
den entsprechenden (gespiegelten) Punkt des Westturms ermitteln kann.
(3 BE)
2.2
Bestimme die Koordinaten des Punktes  des Westturms und gib an, wie weit die beiden Türme am Boden voneinander entfernt sind.
des Westturms und gib an, wie weit die beiden Türme am Boden voneinander entfernt sind.
(4 BE)
3
Beide Türme haben jeweils  Etagen, die alle die gleiche Höhe besitzen. Um die Etagen eines Turms mit einem Aufzug zu erreichen, wäre ein vertikaler Aufzugschacht notwendig.
Etagen, die alle die gleiche Höhe besitzen. Um die Etagen eines Turms mit einem Aufzug zu erreichen, wäre ein vertikaler Aufzugschacht notwendig.
Zeige, dass es möglich ist, alle Etagen eines Turms mit nur einem am Boden beginnenden durchgängigen Aufzugschacht zu erreichen, der in Nord-Süd-Richtung und in Ost-West-Richtung jeweils misst. Die Deckenstärken der Etagen und die Wandstärken der Außenwände sollen hierbei vernachlässigt werden.
misst. Die Deckenstärken der Etagen und die Wandstärken der Außenwände sollen hierbei vernachlässigt werden.
Zeige, dass es möglich ist, alle Etagen eines Turms mit nur einem am Boden beginnenden durchgängigen Aufzugschacht zu erreichen, der in Nord-Süd-Richtung und in Ost-West-Richtung jeweils
(6 BE)
4
Vor einigen Jahren plante man, auf dem südlichen Vorplatz der beiden Türme einen Obelisken zu errichten. Ein Obelisk ist ein nach oben schmaler werdender Pfeiler. Der Mittelpunkt  seiner Grundfläche sollte so auf dem Erdboden platziert werden, dass er mit den Mittelpunkten der Bodenflächen der Türme ein gleichseitiges Dreieck bildet. Bestimme die Koordinaten des zur Umsetzung dieser Planung benötigten Punktes
seiner Grundfläche sollte so auf dem Erdboden platziert werden, dass er mit den Mittelpunkten der Bodenflächen der Türme ein gleichseitiges Dreieck bildet. Bestimme die Koordinaten des zur Umsetzung dieser Planung benötigten Punktes  in der
in der  -
- -Ebene.
-Ebene.
(8 BE)
5
An einem Tag im März 2021 scheint die Sonne um  Uhr näherungsweise aus südlicher Richtung auf die Puerta de Europa und den inzwischen im Mittelpunkt
Uhr näherungsweise aus südlicher Richtung auf die Puerta de Europa und den inzwischen im Mittelpunkt  der Grundfläche aus Aufgabe 4 errichteten,
der Grundfläche aus Aufgabe 4 errichteten,  hohen Obelisken. Die Spitze des Obelisken liegt in vertikaler Richtung genau oberhalb des Punktes
hohen Obelisken. Die Spitze des Obelisken liegt in vertikaler Richtung genau oberhalb des Punktes  Der Vektor
Der Vektor  beschreibt für einen sehr eng begrenzten Zeitraum in guter Näherung die Richtung der Sonnenstrahlen. Der Parameter
beschreibt für einen sehr eng begrenzten Zeitraum in guter Näherung die Richtung der Sonnenstrahlen. Der Parameter  steht dabei für die Zeit nach
steht dabei für die Zeit nach  Uhr in Stunden. Es gilt
Uhr in Stunden. Es gilt 
5.1
Berechne den Winkel, in dem die Sonnenstrahlen um  Uhr auf den Erdboden treffen und den Schattenpunkt der Spitze des Obelisken auf dem Erdboden zu dieser Uhrzeit.
Uhr auf den Erdboden treffen und den Schattenpunkt der Spitze des Obelisken auf dem Erdboden zu dieser Uhrzeit.
[Hinweis: Solltest du die Koordinaten des Punktes in Aufgabe 4 nicht bestimmt haben, verwende stattdessen den Ersatzpunkt
in Aufgabe 4 nicht bestimmt haben, verwende stattdessen den Ersatzpunkt  ]
]
[Hinweis: Solltest du die Koordinaten des Punktes
(8 BE)
5.2
Berechne die Matrix, die den Schattenwurf eines beliebigen Punktes  mit
mit  auf die
auf die  -
- -Ebene für den durch den Definitionsbereich für
-Ebene für den durch den Definitionsbereich für  gegebenen Zeitraum beschreibt.
gegebenen Zeitraum beschreibt.
Bildnachweise
(7 BE)
No machine-readable author provided. Manuel González Olaechea assumed (based on copyright claims)., TorresKio, CC BY 3.0
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
1.2
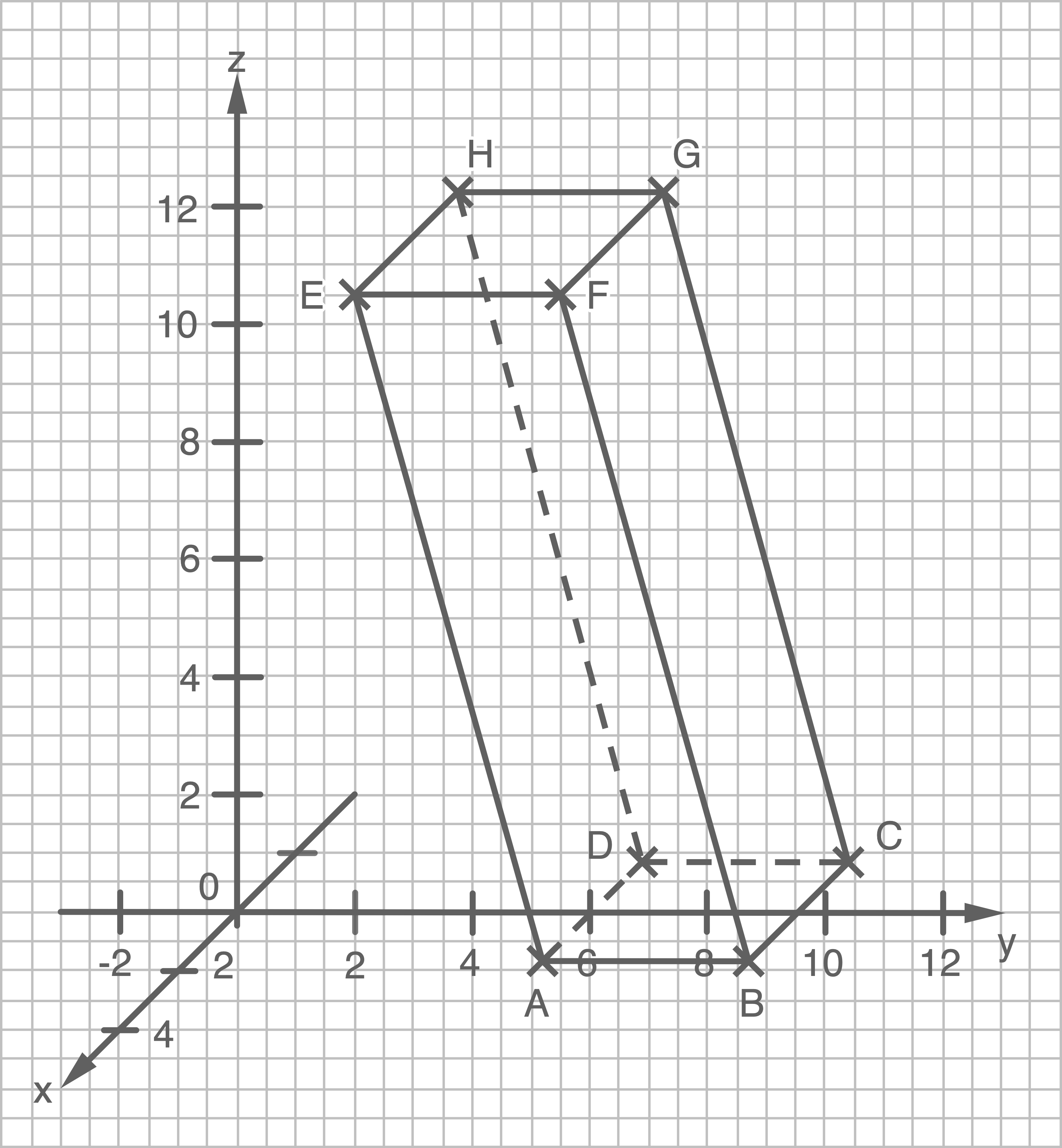
Skizze des Ostturms
1.3
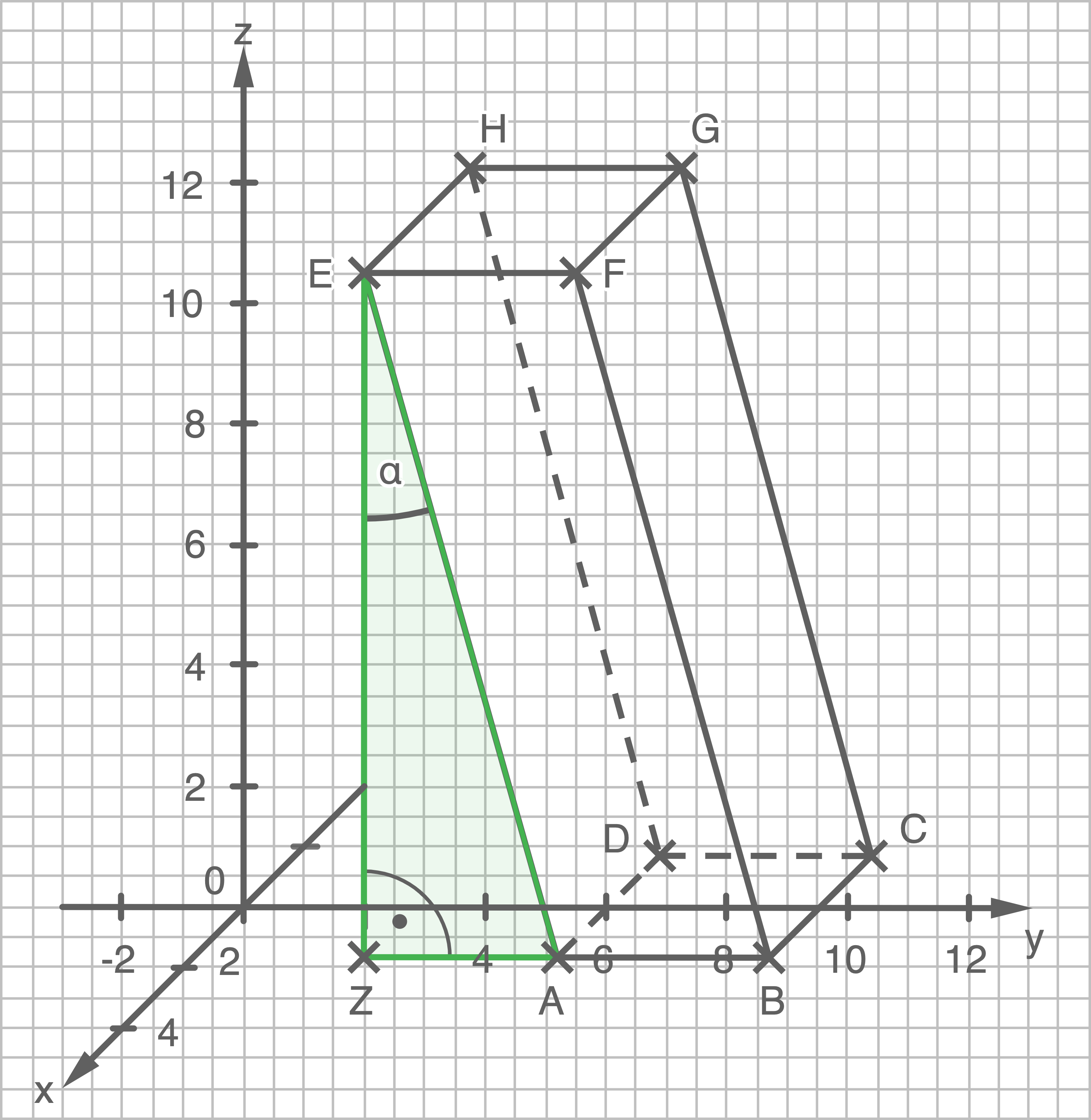
Hilfsskizze
2.1
Wird ein Punkt  an der
an der  -
- -Ebene gespiegelt, ergibt sich der Punkt
-Ebene gespiegelt, ergibt sich der Punkt  Die Gleichung
Die Gleichung  wird durch die Spiegelmatrix
wird durch die Spiegelmatrix  gelöst, da diese das Vorzeichen der
gelöst, da diese das Vorzeichen der  -Koordinate ändert, während die
-Koordinate ändert, während die  - und die
- und die  -Koordinate gleich bleiben.
-Koordinate gleich bleiben.
2.2
Die Punkte
3
Der Aufzugsschacht soll vertikal sein. Der Punkt  wird als ein Eckpunkt gewählt.
wird als ein Eckpunkt gewählt.  entsprechen
entsprechen  Damit ergeben sich die folgenden Koordinaten für die restlichen Eckpunkte des Aufzugsschachts im Boden:
Damit ergeben sich die folgenden Koordinaten für die restlichen Eckpunkte des Aufzugsschachts im Boden:



 Die Koordinaten des Aufzugsschachts in der Dachfläche liegen
Die Koordinaten des Aufzugsschachts in der Dachfläche liegen  über der Grundfläche und sind damit gegeben durch:
über der Grundfläche und sind damit gegeben durch:




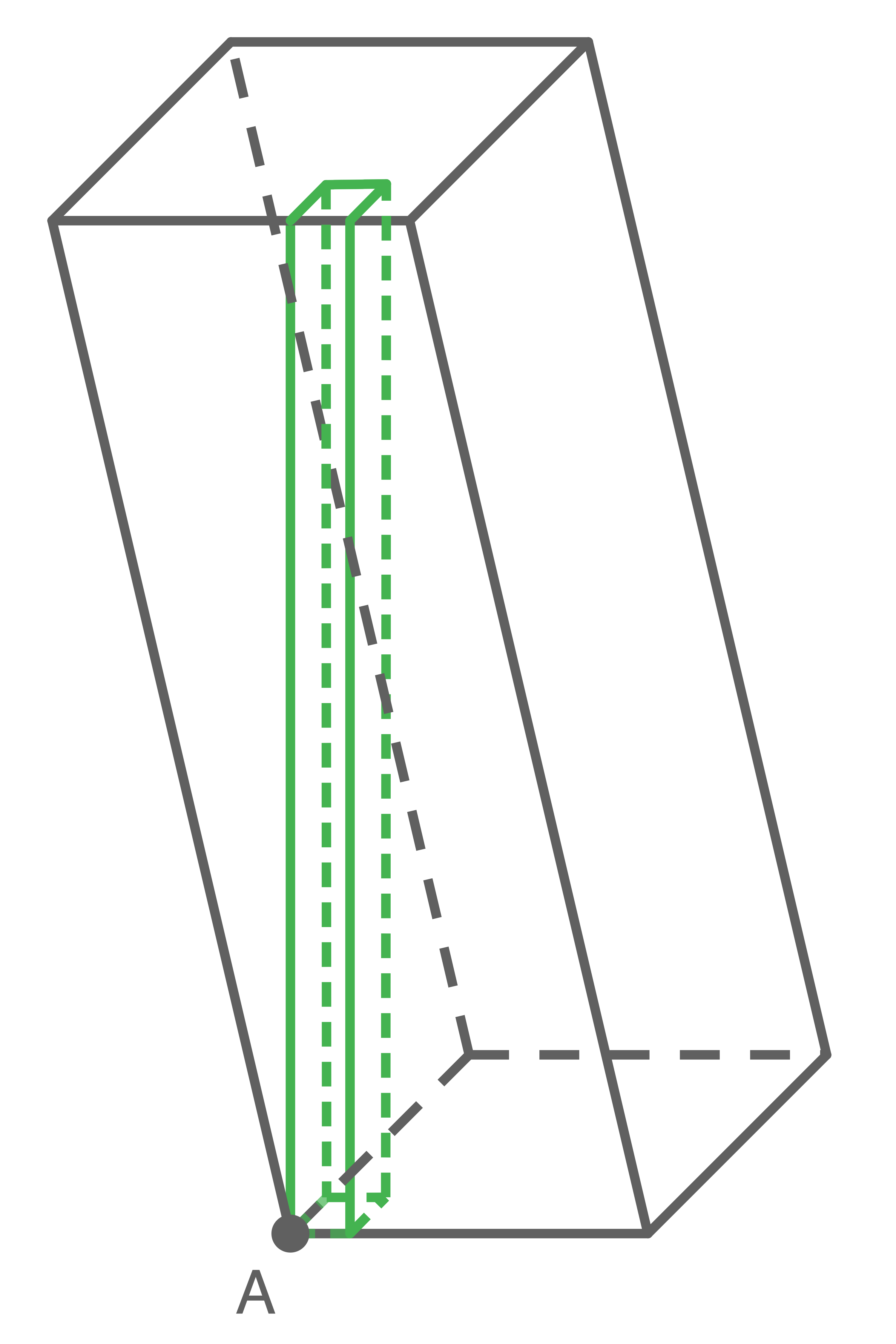
Skizze (nicht maßstäblich)
- Für die
-Koordinate:
- Für die
-Koordinate:
- Für die
-Koordiante:
4
Außerdem wird aus der dreidimensionalen Ansicht des Turms ersichtlich, dass der Punkt  auf der
auf der  -Achse liegt. Dabei lassen sich die
-Achse liegt. Dabei lassen sich die  -Koordinaten durch den Satz des Pythagoras berechnen:
Damit lauten die Koordinaten des Punktes
-Koordinaten durch den Satz des Pythagoras berechnen:
Damit lauten die Koordinaten des Punktes 
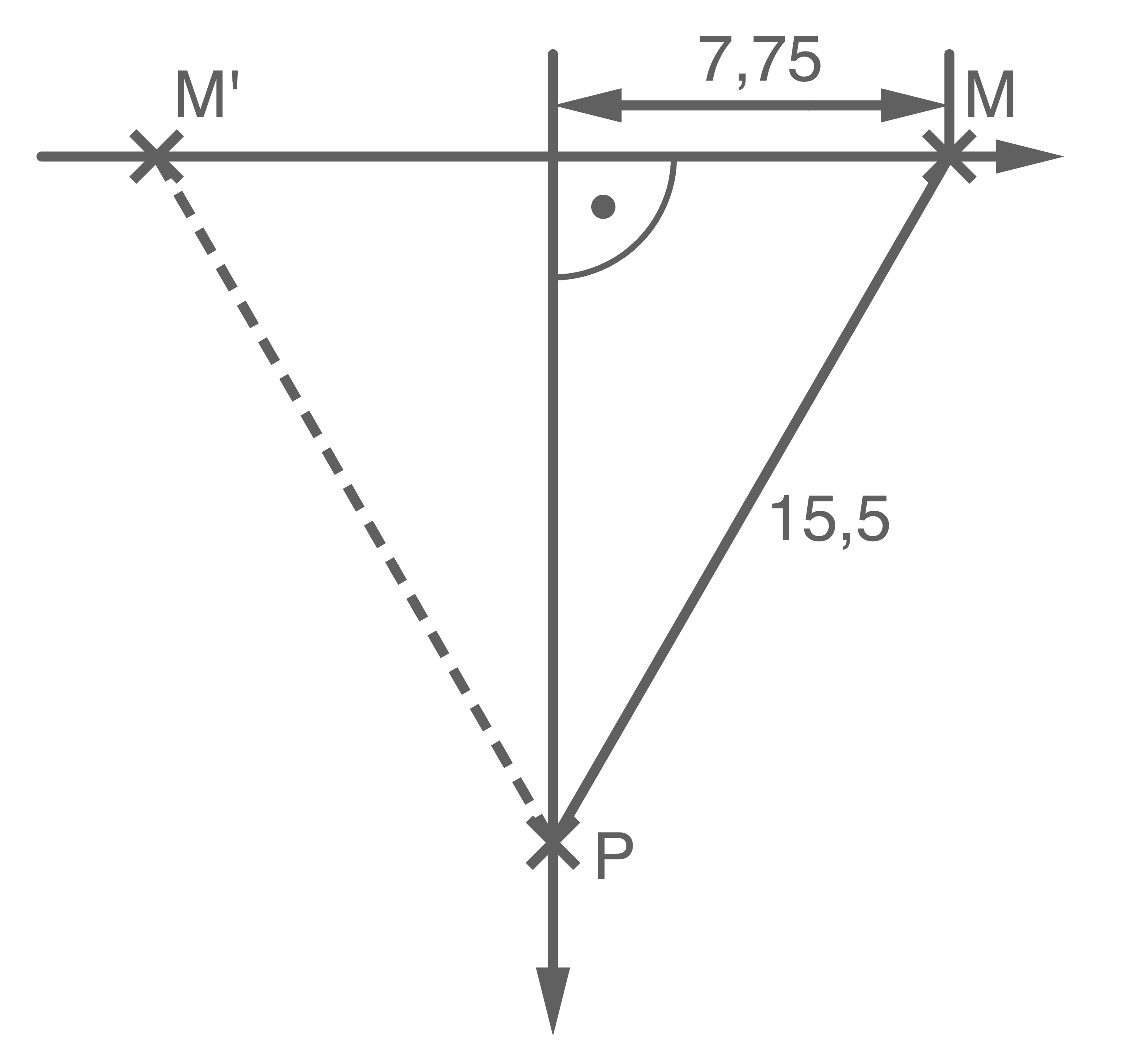
Sicht von oben
5.1
Winkel berechnen
Mit einem Normalenvektor  der Bodenfläche und dem Richtungsvektor
der Bodenfläche und dem Richtungsvektor  der Sonnenstrahlen um
der Sonnenstrahlen um  Uhr folgt:
Daraus folgt
Uhr folgt:
Daraus folgt  Koordinaten des Schattenpunkts berechnen
Um die Koordinaten des Schattenpunkts der Spitze zu berechnen, muss die Gerade der Sonnenstrahlen durch die Spitze
Koordinaten des Schattenpunkts berechnen
Um die Koordinaten des Schattenpunkts der Spitze zu berechnen, muss die Gerade der Sonnenstrahlen durch die Spitze  des Obelisken bestimmt werden:
des Obelisken bestimmt werden:
 Dann entspricht der Schattenpunkt der Spitze gerade dem Schnittpunkt der Geraden
Dann entspricht der Schattenpunkt der Spitze gerade dem Schnittpunkt der Geraden  mit der
mit der  -
- -Ebene, welche durch die Ebenengleichung
-Ebene, welche durch die Ebenengleichung  beschrieben wird.
Durch Einsetzen der Geraden in die Ebenengleichung folgt:
beschrieben wird.
Durch Einsetzen der Geraden in die Ebenengleichung folgt:
![\(\begin{array}[t]{rll}
9,3 - k \cdot 1,2 &=& 0&\quad \scriptsize \mid\; +k \cdot 1,2 \\[5pt]
9,3 &=& k\cdot 1,2 &\quad \scriptsize \mid\; :1,2 \\[5pt]
7,75&=& k
\end{array}\)](https://mathjax.schullv.de/5aa10e47504d773087b384aaabeedd72912b092dfadfd37336a9156d7b75b245?color=5a5a5a) Durch Einsetzen von
Durch Einsetzen von  in die Geradengleichung
in die Geradengleichung  ergibt sich:
ergibt sich:

 Die Koordinaten des Schattenpunktes der Spitze des Obelisken lauten somit
Die Koordinaten des Schattenpunktes der Spitze des Obelisken lauten somit  .
.
5.2
Zunächst wird eine Geradengleichung mit Stützvektor  und dem Richtungsvektor der Sonnenstrahlen
und dem Richtungsvektor der Sonnenstrahlen  aufgestellt:
Der Schattenpunkt von
aufgestellt:
Der Schattenpunkt von  ergibt sich durch Einsetzen der Geraden in die
ergibt sich durch Einsetzen der Geraden in die  -
- -Ebene, welche beschrieben wird durch
-Ebene, welche beschrieben wird durch  Durch Einsetzen in
Durch Einsetzen in  lässt sich der Ortsvektor des Schattenpunkts
lässt sich der Ortsvektor des Schattenpunkts  berechnen:
Mit der Matrix-Vektor-Multiplikation kann
berechnen:
Mit der Matrix-Vektor-Multiplikation kann  wie folgt umgeformt werden:
Damit ist
wie folgt umgeformt werden:
Damit ist  die gesuchte Abbildungsmatrix.
die gesuchte Abbildungsmatrix.