C2 - Stochastik

Linkshänder nutzen für Tätigkeiten wie Schreiben oder Werfen bevorzugt ihre linke Hand. $15\,\%$ der Bevölkerung sind Linkshänder. In einem Einkaufszentrum werden Personen zufällig ausgewählt und nacheinander danach befragt, ob sie Linkshänder sind.

1.1

Begründe, warum diese Befragung als Bernoulli-Kette aufgefasst werden kann.

(2 BE)

1.2

Berechne die Wahrscheinlichkeit, spätestens bei der dritten befragten Person zum ersten Mal auf einen Linkshänder zu treffen.

(3 BE)

1.3

Gib für die Ereignisse $A$ und $B$ jeweils eine geeignete Zufallsvariable an und bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:

Unter $70$ befragten Personen befinden sich genau $10$ Linkshänder.

Unter $100$ befragten Personen befinden sich mindestens so viele Rechtshänder, wie zu erwarten ist.

Unter $50$ befragten Personen befinden sich genau zwei Linkshänder. Sie werden direkt hintereinander befragt.

(9 BE)

1.4

Berechne die Anzahl an Personen, die man mindestens befragen muss, um mit einer Wahrscheinlichkeit von mindestens $95\,\%$ auf mindestens einen Linkshänder zu treffen.

(4 BE)

Ob jemand Rechts- oder Linkshänder wird, lässt sich bereits in der frühen Schwangerschaft absehen. Neun von zehn Ungeborenen bevorzugen im Mutterleib den rechten Daumen zum Lutschen (Rechtslutscher).
Forscher fanden heraus, dass alle Kinder, die rechts gelutscht hatten, im Alter von $10$ bis $12$ Jahren Rechtshänder waren.
Zwei Drittel der Kinder, die im Mutterleib am linken Daumen lutschten (Linkslutscher), waren im Alter von $10$ bis $12$ Jahren Linkshänder.

2.1

Stelle den Sachverhalt in einem vollständig ausgefüllten Baumdiagramm oder einer vollständig ausgefüllten Vierfeldertafel dar.

(4 BE)

2.2

Bestimme die Wahrscheinlichkeit dafür, dass ein Kind, das im Alter von $10$ bis $12$ Jahren Rechtshänder ist, im Mutterleib am linken Daumen gelutscht hat.

(3 BE)

Forscher vermuten seit Längerem, dass der Anteil an Linkshändern in der Bevölkerung größer als $15\,\%$ ist. Zur Überprüfung ihrer Vermutung werden $300$ Personen zufällig ausgewählt und danach befragt, ob sie Linkshänder sind.

3.1

Entwickle einen Hypothesentest auf einem Signifikanzniveau von $2,5\,\%$ .
Formuliere eine geeignete Entscheidungsregel im Sachzusammenhang.

(6 BE)

3.2

Der tatsächliche Anteil an Linkshändern in der Bevölkerung betrage $18\,\%$ . Beschreibe den Fehler 2. Art im Sachzusammenhang und bestimme seine Wahrscheinlichkeit.

(5 BE)

Bei einem Reaktionstest, an dem sehr viele Linkshänder teilnahmen, musste beim Auftreten eines Signals mit der rechten Hand möglichst schnell eine Taste betätigt werden.
Die Tabelle zeigt die nach der Auswertung aller Daten zusammengefassten Ergebnisse.

Reaktionszeit in Sekunden	Anteil in %
bis $0,2$	$7$
über $0,2$ bis $0,4$	$14$
über $0,4$ bis $0,6$	$51$
über $0,6$ bis $0,8$	$18$
über $0,8$ bis $1,0$	$10$

4.1

Stelle die Verteilung der gemessenen Reaktionszeiten graphisch dar.
Vereinfachend wird davon ausgegangen, dass die in der Tabelle angegebenen prozentualen Anteile den Wahrscheinlichkeiten der Werte in den Intervallmitten der gemessenen Reaktionszeiten entsprechen.
Berechne unter Verwendung der Intervallmitten den Erwartungswert und die Standardabweichung der gemessenen Reaktionszeiten.

[zur Kontrolle: $\mu = 0,52;$ $\sigma \approx 0,20$ ]

(6 BE)

4.2

Begründe durch Angabe von zwei unterschiedlichen Argumenten, dass die Zufallsvariable $Z$ : "gemessene Reaktionszeit der Versuchspersonen in Sekunden" näherungsweise als normalverteilt angenommen werden kann.

(3 BE)

4.3

Gehe davon aus, dass die gemessene Reaktionszeit in Sekunden normalverteilt ist mit den in Aufgabe 4.1 berechneten Werten.
Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse.

$D:$ Die Reaktionszeit einer zufällig herausgegriffenen Person beträgt höchstens $0,45$ Sekunden.

$E:$ Die Reaktionszeit einer zufällig herausgegriffenen Person weicht höchstens um die halbe Standardabweichung vom Erwartungswert ab.

(5 BE)

1.1

Diese Befragung kann als Bernoulli-Kette aufgefasst werden, da bei jeder neuen Befragung immer nur zwei Möglichkeiten existieren, denn entweder ist die befragte Person Linkshänder oder nicht. Dabei kann davon ausgegangen werden, dass sich die Wahrscheinlichkeiten für die beiden Möglichkeiten nicht ändern, da verhältnismäßig die Anzahl der Befragten ziemlich gering zur Gesamtbevölkerung ist und somit die beiden Ausgänge der einzelnen Versuche unabhängig voneinander sind.

1.2

$P(E)=0,15+0,85\cdot0,15$ $+0,85\cdot0,85\cdot0,15$ $=0,3859$

Die Wahrscheinlichkeit, spätestens bei der dritten befragten Person zum ersten Mal auf einen Linkshänder zu treffen, beträgt etwa $38,6\,\%$ .

1.3

Ereignis $A$ :

$X$ ist binomialverteilt mit $B_{70;0,15}$ und beschreibt die Anzahl der Linkshänder unter den befragten Personen

$P(A)\approx0,1332$

Vollständige Lösung anzeigen

Die Wahrscheinlichkeit, dass sich unter $70$ befragten Personen genau $10$ Linkshänder befinden, beträgt etwa $13,32\,\%$ .

Ereignis $B$ :

$Y$ ist binomialverteilt mit $B_{100;0,85}$ und beschreibt die Anzahl der Rechtshänder unter den befragten Personen

$E(X)=n\cdot p=100\cdot 0,85=85$

$\begin{array}[t]{rll} P(B)=P(Y\geq 85)&=&1-P(Y\leq84)\quad\\[5pt] &=& 1-F_{100;0,85}(84)\\[5pt] &\approx&1-0,4317\quad\\[5pt] &\approx&0,5683 \end{array}$

Die Wahrscheinlichkeit, dass sich unter $100$ befragten Personen mindestens so viele Rechtshänder sind, wie zu erwarten ist, beträgt etwa $56,83\,\%$ .

Ereignis $C$ :

Damit sich unter $50$ befragten Personen genau zwei Linkshänder befinden, die direkt hintereinander befragt werden, existieren $49$ verschiedene Anordnungsmöglichkeiten:

$P(C)=49\cdot 0,15^2\cdot 0,85^{48}\approx0,00045$

Die Wahrscheinlichkeit für das Ereignis $C$ beträgt etwa $0,045\,\%$ .

1.4

$n\approx18,43$

Vollständige Lösung anzeigen

Man muss mindestens $19$ Personen befragen, um mit einer Wahrscheinlichkeit von mindestens $95\,\%$ auf mindestens einen Linkshänder zu treffen.

2.1

RL: Rechtslutscher
LL: Linkslutscher
RH: Rechtshänder
LH: Linkshänder

Baumdiagramm:

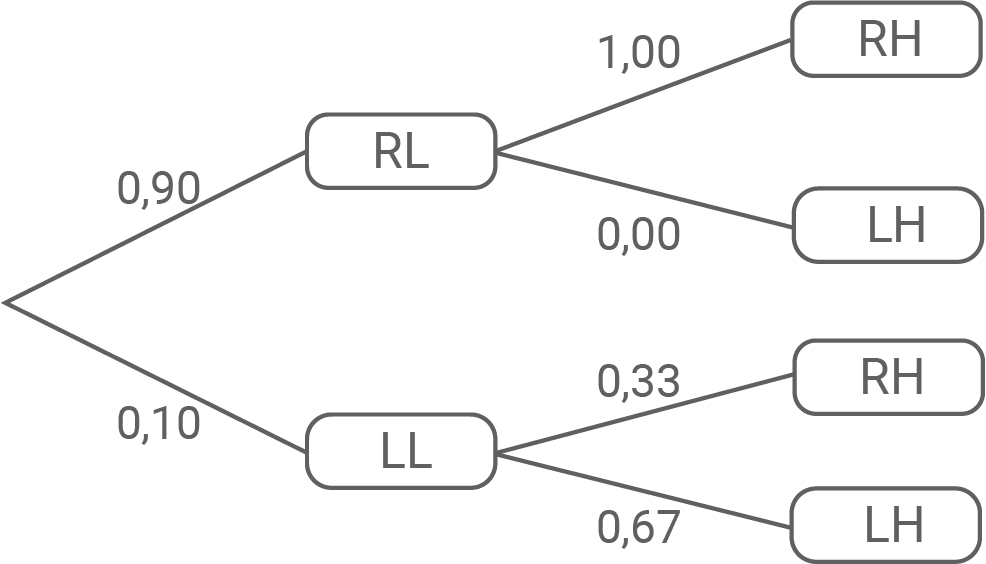
Vierfeldertafel:

	$LH$	$RH$
$LL$	$\dfrac{2}{30}$	$\dfrac {1}{30}$	$\dfrac{1}{10}$
$RL$	$0$	$\dfrac{9}{10}$	$\dfrac{9}{10}$
	$\dfrac{2}{30}$	$\dfrac{28}{30}$	$1$

2.2

$P_{RH}(LL)=\dfrac{P(LL\cap RH)}{RH}$ $=\dfrac{\frac{1}{30}}{\frac{28}{30}}=\dfrac{1}{28}\approx0,0357$

Die Wahrscheinlichkeit dafür, dass ein Kind im Alter von 10 bis 12 Jahren Rechtshänder ist, aber im Mutterleib am linken Daumen gelutscht hat, beträgt etwa $3,57\,\%$ .

3.1

Nullhypothese: $H_0:\,p=0,15$
Alternative: $H_1:\,p\gt0,15$

Es handelt sich um einen rechtsseitigen Hypothesentest.
Die Zufallsvariable $X$ beschreibt die Anzahl der Linkshänder unter den befragten Personen und ist binomialverteilt mit $n=300.$

$F_{300;0,15}(57)\approx 0,9756$

Vollständige Lösung anzeigen

Somit gilt: $k-1=57$ , also ist $k=58$ .
Der Ablehnungsbereich $A$ ist dadurch $A=\text{ { 58, ... ,300}}$

Befinden sich unter den 300 befragten Personen mindestens 58 Linkshänder, so wird die Nullhypothese verworfen und die Forscher können mit einem Signifikanzniveau von $2,5\,\%$ davon ausgehen, dass der Anteil an Linkshänder in der Bevölkerung höher als $15\,\%$ ist, ansonsten nicht.

3.2

Ein Fehler 2. Art liegt vor, wenn die Nullhypothese falsch ist, jedoch nicht verworfen wird. In diesem Sachzusammenhalt bedeutet dies, dass die Forscher aus ihren Testergebnissen schließen, dass der Anteil an Linkshänder in der Bevölkerung weiterhin $15\,\%$ beträgt, obwohl er in Wirklichkeit größer ist.

$X:$ Anzahl der Linkshänder unter den befragten Personen, $\quad n=300\,,\quad p=0,18$

$\begin{array}[t]{rll} \beta&=&P_{p=0,18}(X\leq57) &\quad \\[5pt] &=&F_{300;0,18}(57) &\quad \\[5pt] &\approx& 0,705&\quad \end{array}$

Die Wahrscheinlichkeit beträgt etwa $70,5\,\%$ .

4.1

Erwartungswert der gemessenen Reaktionszeiten:
$\mu =0,1\cdot 0,07+0,3\cdot0,14$ $+0,5\cdot0,51+0,7\cdot0,18$ $+0,9\cdot 0,1=0,52$

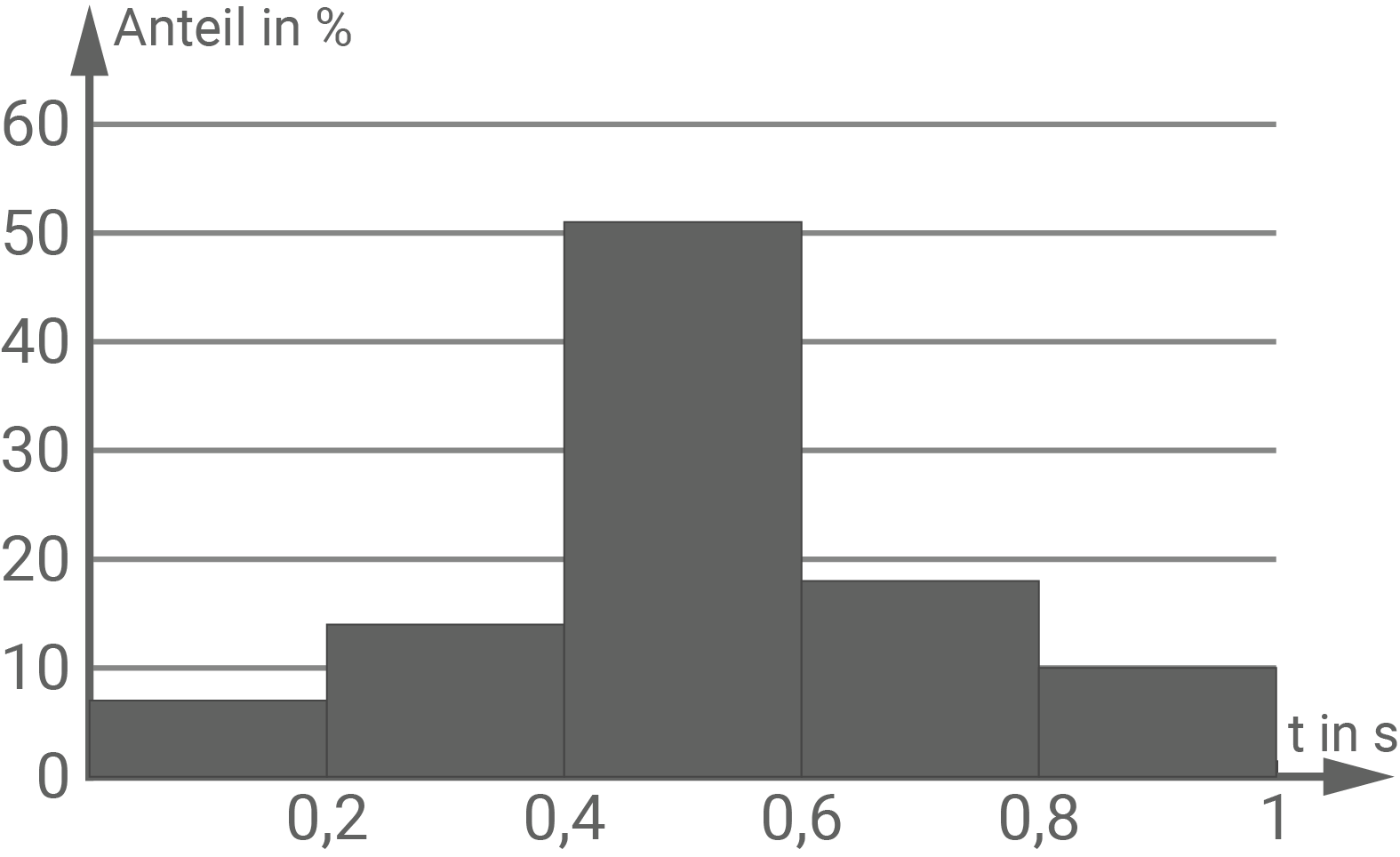
Varianz der gemessenen Reaktionszeiten:
$V(x)=(0,1-0,52)^2\cdot 0,07$ $+(0,3-0,52)^2\cdot0,14$ $+(0,5-0,52)^2\cdot0,51$ $+(0,7-0,52)^2\cdot0,18$ $+(0,9-0,52)^2\cdot 0,1$ $=0,0396$

Standardabweichung der gemessenen Reaktionszeiten:
$\sigma=\sqrt{V(x)}=\sqrt{0,0396}\approx0,2$

4.2

Die Zufallsvariable $Z$ kann näherungsweise als normalverteilt angenommen werden, da die Reaktionszeit jedes teilnehmenden Linkshänders jeden Wert in dem Zeitintervall $[0;1]$ annehmen kann. Dabei nimmt $Z$ im Intervall [0,4;0,6] die größten Wahrscheinlichkeitswerte an, bei steigender Entfernung der Werte der Zufallsvariable von diesem Intervall sinken die zugehörigen Wahrscheinlichkeiten annähernd symmetrisch, sodass annähernd die charakteristische Glockenkurve entsteht.

4.3

$Z$ ist normalverteilt mit $\mu=0,52$ und $\sigma=0,2$

Ereignis $D$ :

$P(D)=P(Z\leq0,45)\approx0,36$

Ereignis $E$ :

halbe Standardabweichung: $0,1$

$P(E)=P(0,52-0,1\leq Z\leq0,52+0,1)$ $=P(0,42\leq Z\leq0,62)\approx0,38$