B1 - Analysis

Rückhaltebecken für Regen dienen dazu, bei starkem Regen Überschwemmungen zu vermeiden, indem das Regenwasser zunächst darin gesammelt und später langsam wieder abgelassen wird.
Die Zuflussrate des Regenwassers kann bei einigen Regenfällen modelliert werden durch die Funktionenschar $f_k$ mit

$f_k(t)=100(k^2 \cdot t+k) \cdot e^{-\frac{k}{5}\cdot t},$ $t\geq 0, k \in \mathbb{R}^+.$

Dabei gibt $t$ die Zeit in Stunden nach Beobachtungsbeginn und $f_k(t)$ die Zuflussrate in $\dfrac{m^3}{h}$ an.
Der Parameter $k$ ist ein Maß für die Stärke des Regens.

1.1

Berechne die Zuflussrate zum Zeitpunkt $t=0$ in Abhängigkeit vom Parameter $k$ .

(2 BE)

1.2

Berechne die maximale Zuflussrate und den zugehörigen Zeitpunkt jeweils in Abhängigkeit vom Parameter $k$ .
Die zweite Ableitung $\(f_k$ kann ohne Nachweis verwendet werden.

[Zur Kontrolle: $t_{max}=\dfrac{4}{k}$ ]

(7 BE)

1.3

Untersuche den Einfluss des Parameters $k$ für $1\leq k\leq 4$ auf den Zeitpunkt und die Größe der maximalen Zuflussrate.
Bestimme die Funktionsgleichung der Ortskurve der Hochpunkte.

(5 BE)

1.4

Bestimme die Wendepunkte der Graphen der Scharfunktionen $f_k$ in Abhängigkeit von $k$ .
Ermittle die Gleichung der Funktionenschar $w_k$ , deren Graphen die Wendetangenten der Graphen der Scharfunktionen $f_k$ beschreiben.

[Zur Kontrolle: $w_k(t)= 100k \cdot (19-k \cdot t) \cdot e^{-\frac{9}{5}}$ ]

(8 BE)

1.5

Das nötige Fassungsvermögen des Rückhaltebeckens, das für die Aufnahme der gesamten Regenmenge bei einer Modellierung der Zuflussrate durch die Funktionenschar $f_k$ ausreicht, kann mittels zweier Verfahren bestimmt werden:

(1) Bestimmung des Grenzwerts $\lim\limits_{u\to\infty}[F_k(u)-F_k(0)],$ wobei $F_k$ eine Stammfunktionenschar der $f_k$ Funktionenschar darstellt.

(2) Bestimmung des Inhalts der Fläche, die zwischen den Koordinatenachsen und der Wendetangente $w_k$ eingeschlossen ist.

1.5.1

Mit einem der beiden Verfahren wird der genaue Wert für das nötige Fassungsvermögen ermittelt und mit dem anderen lediglich eine Näherungslösung.
Entscheide, mit welchem der beiden Verfahren bei der vorgegebenen Modellierung der genaue Wert für das nötige Fassungsvermögen bestimmt wird, und erläutere deine Entscheidung.

(3 BE)

1.5.2

Bestimme eine Stammfunktionenschar $F_k$ von $f_k$ und berechne den Wert für das nötige Fassungsvermögen nach Verfahren (1).

(3 BE)

1.5.3

Bestimme den Wert für das nötige Fassungsvermögen nach Verfahren (2) und vergleiche diesen mit dem Wert aus Aufgabe 1.5.2, indem du die prozentuale Abweichung der Näherungslösung ermittelst.

(3 BE)

Die obere Randkurve des um $90\,^{\circ}$ gekippten rotationssymmetrischen Rückhaltebeckens in Material 2 kann durch den Graphen der Funktion $g$ mit $g(x) = \sqrt{60x}, \, x \geq 0$ , modelliert werden.
Die Tiefe des Rückhaltebeckens wird mit $H$ und der Durchmesser mit $d$ bezeichnet.
Alle Längenangaben erfolgen dabei in Meter.

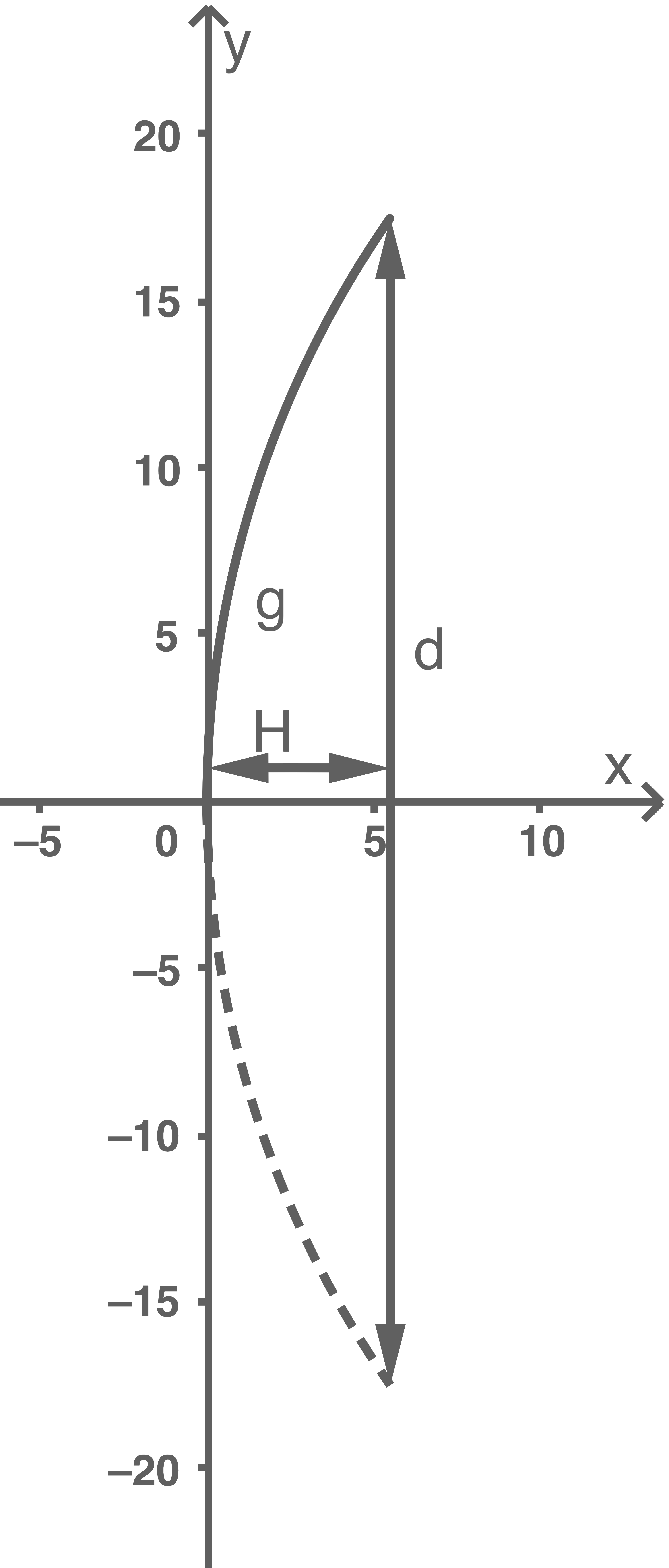
Material 2: Skizze des (um $90\,^{\circ}$ gekippten) Rückhaltebeckens

2.1

Zeige, dass für das Volumen des Rückhaltebeckens $V =\pi \cdot 30H^2$ gilt.
Berechne die Tiefe $H$ und den Durchmesser $d$ des Rückhaltebeckens, wenn dieses ein Fassungsvermögen von $3000\,\text{m}^3$ besitzt.

(5 BE)

2.2

Das vollgelaufene Rückhaltebecken wird bei konstanter Abflussrate in $100$ Stunden wieder völlig entleert.

2.2.1

Entscheide ohne eine Rechnung, ob nach $50$ Stunden die Höhe des Wasserstandes im Rückhaltebecken auf der halben Höhe über dem Beckenboden oder darüber bzw. darunter liegt.

(2 BE)

2.2.2

Begründe, dass für die Regenwassermenge (in $\,\text{m}^3$ ), die sich zum Zeitpunkt $t$ nach Beginn der Entleerung noch im Rückhaltebecken befindet, gilt:

$V(t) =-30t+ 3000$

(3 BE)

2.2.3

Leite mithilfe der Formeln aus Aufgabe 2.1 und Aufgabe 2.2.2 für die Höhe des Wasserstands über dem Beckenboden bei der Entleerung die Formel $h(t)= \sqrt{ \dfrac{1}{\pi} (100-t)}$ her.

(4 BE)

Die obere Randkurve des um $90^{\circ}$ gekippten Rückhaltebeckens kann alternativ durch den Graphen einer Funktion $r$ der Form $\;r(x)=a\cdot\ln(x+b)\;$ mit $a,\;b\gt0$ modelliert werden.
Bestimme mit Hilfe der Funktion $g$ aus Aufgabe 2 die Parameter $a$ und $b$ so, dass $r(0)=g(0)$ und $r(5)=g(5)$ gilt.

Bestimme, welche Tiefe und welchen Durchmesser ein rotationssymmetrisches Rückhaltebecken haben müsste, damit es dasselbe Fassungsvermögen von $3000\;\text{m}^3$ wie das Rückhaltebecken aus Aufgabe 2 besitzt.

(5 BE)

1.1

Zuflussrate zum Zeitpunkt $t=0$ in Anhängigkeit vom Parameter $k$ :
$\begin{array}[t]{rll} f_k(0)& = &100(k^2 \cdot 0+k) \cdot \mathrm e^{-\frac{k}{5}\cdot 0}\quad \scriptsize\; \\[5pt] & = &100k \end{array}$

1.2

$\( f_k$

Vollständige Lösung anzeigen

Notwendige Bedingung für Extrema: $\(f$

$\begin{array}[t]{rll} 20\mathrm e^{-\frac{k}{5}t}k^2(4-kt )& = &0&\quad \scriptsize\; \mid :(20\mathrm e^{-\frac{k}{5}t}k^2)\neq0\\[5pt] 4-kt& = &0&\quad \scriptsize\;\mid -4\\[5pt] -kt& = &-4&\quad \scriptsize\; \mid :(-k), \text{ da }k\in\mathbb{R}^+\\[5pt] t& = &\dfrac{4}{k}\quad \scriptsize\;\\[5pt] \end{array}$

Hinreichende Bedingung für Extrema: $\(f$ und $\(f$

$\(\begin{array}[t]{rll} f_k$

$\begin{array}[t]{rll} f_k\bigg(\dfrac{4}{k}\bigg)& = &100(k^2\cdot \dfrac{4}{k}+k) \cdot \mathrm e^{-\frac{k}{5}\cdot \frac{4}{k}}\quad \scriptsize\; \\[5pt] & = &500k\cdot \mathrm e^{-\frac{4}{5}} \end{array}$

Die Zuflussrate ist nach $t=\dfrac{4}{k}$ Stunden mit $500k\cdot \mathrm e^{-\frac{4}{5}}$ $\frac{\text{m}^3}{\text{h}}$ maximal.

1.3

Hochpunkt des Graphen von $f_k$ für $1\leq k\leq4$ bestimmen:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 6: Graph analysieren $\to$ 3: Maximum

$\blacktriangleright$ Casio Classpad II

Analyse $\to$ Grafische Lösung $\to$ Maximum

Je größer $k$ ist, desto früher ist der Zeitpunkt und desto höher ist die Größe der maximalen Zuflussrate.

Funktionsgleichung der Ortskurve der Hochpunkte
$t$ nach $k$ umformen:

$t=\dfrac{4}{k}\Leftrightarrow k=\dfrac{4}{t}$

$k$ in $y=500k\cdot\mathrm e^{-\frac{4}{5}}$ einsetzen:

$\begin{array}[t]{rll} y& = & 500\cdot \dfrac{4}{t}\cdot \mathrm e^{-\frac{4}{5}} & = &\dfrac{2000}{t}\cdot \mathrm e^{-\frac{4}{5}} \end{array}$ mit $t\gt0$

1.4

Wendepunkte der Graphen der Funktionsschar $f_k$ :

Notwendige Bedingung $\(f_k$ für Wendestellen in Abhängigkeit von $k,$ mit der Solve-Funktion des CAS Taschenrechners anwenden:

$\begin{array}[t]{rll} 4k^3(kt -9) \cdot\mathrm e^{-\frac{k}{s}t}& = &0\\[5pt] t_k & = &\dfrac{9}{k} \end{array}$

Zuflussrate durch Einsetzen von $t_k$ in $f_k(t)$ ermitteln und Lösen mit der Solve-Funktion des CAS:

$f_k\left(\dfrac{9}{k}\right)=1000k\cdot \mathrm e^{-\frac{9}{5}}$

Die Wendepunkte der Graphen der Funktionsschar $f_k$ liegen bei $W_k\left(\frac{9}{k}\mid1000k\cdot \mathrm e^{-\frac{9}{5}}\right).$

Bestimmen der Gleichung der Wendetangente durch die Solve-Funktion des CAS:

$\(w_k(t)=f_k$

$f_k\left(\dfrac{9}{k}\right)=1000k \mathrm e^{-\frac{9}{5}}$

$\(f_k$

Einsetzen in die Gleichung der Wendetangente $w_k$ :

$w_k(t)=100k\mathrm e^{-\frac{9}{5}}(19-kt)$

1.5.1

Mit dem Verfahren (1) wird der genaue Wert für das Fassungsvermögen ermittelt, da durch die Scharfunktionen $f_k$ die Zuflussrate beschrieben wird (und $f_k(t)\gt 0$ für $t\geq0$ ), gibt der mit Hilfe der Stammfunktion $F_k$ von $f_k$ als Grenzwert bestimmte Inhalt der Fläche zwischen dem Funktionsgraphen und der positiven $t$ -Achse die Wassermenge an, die insgesamt zufließen kann.
Verfahren (2) ist eine Nährungslösung.

1.5.2

Mit dem CAS folgt:

$F_k=100(-5kt-30)\cdot \mathrm e^{-{\frac{k}{5}t}}$

Verfahren (1):

$\lim\limits_{u\to\infty}[F_k(u)-F_k(0)]=3000$

Vollständige Lösung anzeigen

Nach Verfahren (1) beträgt der Wert für das nötige Fasungsvermögen $3000\,\text{m}^3$ .

1.5.3

Verfahren (2):

Mit dem CAS folgt:

$\begin{array}[t]{rll} w(0)&=& 1900k\cdot \mathrm e^{-\frac{9}{5}} \\[5pt] w_k(t)&=& 0 \\[5pt] 100k\cdot(19-kt)\cdot \mathrm e^{-\frac{9}{5}}& = &0 \\[5pt] t& = &\dfrac{19}{k} \end{array}$

Die Wendetangente bildet mit dem beiden Koordinatenachsen ein rechtwinkliges Dreieck. Der Flächeninhalt $A$ lässt sich somit mit $h=1900k\cdot \mathrm e^{-\frac{9}{5}}$ und $g=\dfrac{19}{k}$ berechnen:

$A=\dfrac{1}{2}\cdot h\cdot g=\dfrac{1}{2}\cdot 1900k\cdot \mathrm e^{-\frac{9}{5}}\cdot \dfrac{19}{k}$ $=18050\cdot \mathrm e^{-\frac{9}{5}}\approx 2983,65\;[\text{VE}]$

Mit $\dfrac{18050\cdot \mathrm e^{-\frac{9}{5}}}{3000}=0,9945$ weicht die Näherungslösung um etwa $0,55\,\%$ ab.

2.1

Volumen des Rückhaltebeckens:
$\begin{array}[t]{rll} V& = &\pi\displaystyle\int_{a}^{b}(g(x))^2\;\mathrm dx \quad \scriptsize \; \\[5pt] V& = &\pi\displaystyle\int_{0}^{H}(\sqrt{60x})^2\;\mathrm dx \quad \scriptsize \; \\[5pt] & = &\pi\displaystyle\int_{0}^{H}60x\;\mathrm dx \quad \scriptsize \; \\[5pt] & = &\pi \cdot\left[30x^2\right]_{0}^H\quad \scriptsize \; \\[5pt] & = &\pi \cdot 30H^2\quad \scriptsize \; \\[5pt] \end{array}$

Höhe $H$ und Durchmesser $d$ bei einem Fassungsvermögen von $3000\,\text{m}^3$ :

Höhe $H$ :

$\begin{array}[t]{rll} \pi \cdot 30H^2& = &3000 &\quad \scriptsize \mid :30\pi\\[5pt] H^2& = &\dfrac{100}{\pi}&\quad \scriptsize \mid \sqrt \; \\[5pt] H& = &\sqrt{\dfrac{100}{\pi}}\,\quad \scriptsize \; \\[5pt] & \approx &5,64\;[\text{m}] \end{array}$

Durchmesser $d$ :

$\begin{array}[t]{rll} 2\cdot g\bigg(\sqrt{\dfrac{100}{\pi}}\bigg)& = &2\cdot \sqrt {60\sqrt{\dfrac{100}{\pi}}} & \approx &36,8\;[\text{m}] \end{array}$

Bei einem Fassungsvermögen von $3000\,\text{m}^3$ beträgt die Höhe $5,64 \,\text{m}$ und der Druchmesser $36,8\,\text{m}$ .

2.2.1

Der Wasserstand im Rückhaltebecken liegt nach 50 Stunden nicht unter der Hälfte der Höhe des Beckens, da das Rückhaltebecken oben einen größeren Durchmesser als unten hat. Somit sinkt die Höhe des Wasserstandes bei konstanter Abflussrate zunächst langsamer und dann immer schneller.

2.2.2

Das Volumen nimmt linear ab, da die Abflussrate konstant ist. Die Steigung $m$ ergibt sich aus den Randbedingungen $V(0)=3000$ und $V(100)=0$ :

$m=\dfrac{0-3000}{100-0}=-30$

Der $y$ -Achsenabschnitt ist durch die Regenwassermenge zu Beginn mit $V(0)=3000$ gegeben.

2.2.3

$\begin{array}[t]{rll} V(t)& = &\pi\cdot 30(h(t))^2&\quad \scriptsize \mid: 30\pi \; \\[5pt] \dfrac{V(t)}{30\pi}& = &h(t)^2&\quad \scriptsize \mid: \sqrt\; \\[5pt] h(t)& = &\sqrt{\dfrac{V(t)}{30\pi}}&\quad \scriptsize \; \\[5pt] & = &\sqrt{\dfrac{-30t+3000}{30\pi}}\quad \scriptsize \\[5pt] & = &\sqrt{\dfrac{-t+100}{\pi}}\quad \scriptsize \\[5pt] & = &\sqrt{\dfrac{1}{\pi}(100-t)}\quad \scriptsize \\[5pt] \end{array}$

Gleichungssystem erstellen und mit dem CAS lösen:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 3: Algebra $\to$ 7

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math1 $\to$ $\{^{\Box}_{\Box}$

$\begin{array}{lrll} \text{I}\quad&a\cdot\ln(0+b)&=& \sqrt{60\cdot0}\\ \text{II}\quad&a\cdot\ln(5+b)&=& \sqrt{60\cdot5} \\ \hline \quad& a&=& 10\cdot\dfrac{\sqrt 3}{\ln(6)}\\ \quad& b&=&1 \\ \end{array}$

$V=\pi\displaystyle\int_{0}^{H}(r(x))^2\;\mathrm dx$

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$V=\pi\cdot300$ $\cdot\dfrac{\ln(H+1)^2(H+1)-2\ln(H+1)(H+1)+2(H+1)}{\ln(6)}$

Mit dem solve-Befehl des CAS folgt:

$H\approx9,9318\;,\quad d\approx23,1198$

Vollständige Lösung anzeigen

Das Rückhaltebecken würde eine Tiefe von ca. $9,93\text{m}$ und einen Durchmesser von ca. $23,12\text{m}$ benötigen, um ein Volumen von $3000\text{m}^3$ Regenwasser halten zu können.