C1 - Stochastik
In der sogenannten PINTA-Studie zur Internetabhängigkeit aus dem Jahr 2011 wurden bundesweit 15023 Personen im Alter von  -
- Jahren befragt, die als repräsentativ für die Gesamtbevölkerung in dieser Altersklasse angesehen werden können. In der folgenden Tabelle sind einige Ergebnisse der Studie dargestellt.
Jahren befragt, die als repräsentativ für die Gesamtbevölkerung in dieser Altersklasse angesehen werden können. In der folgenden Tabelle sind einige Ergebnisse der Studie dargestellt.
 aller Befragten wird demnach als internetabhängig eingestuft; bei
aller Befragten wird demnach als internetabhängig eingestuft; bei  aller Befragten und
aller Befragten und  der weiblichen Befragten der Altersgruppe 14 - 16 Jahren wird die Internetnutzung als problematisch eingestuft.
der weiblichen Befragten der Altersgruppe 14 - 16 Jahren wird die Internetnutzung als problematisch eingestuft.
Die Internetnutzung einer Person kann nicht gleichzeitig als problematisch und als Internetabhängigkeit eingestuft werden. Im Folgenden werden die in der PINTA-Studie ermittelten relativen Häufigkeiten bundesweit für alle Personen im Alter von -
- Jahren als Wahrscheinlichkeiten angesehen.
Jahren als Wahrscheinlichkeiten angesehen.
Binomialsummenfunktion 


 für
für 
Die Werte  und
und  bedeuten: Die angegebenen Wahrscheinlichkeiten sind auf vier Stellen gerundet
bedeuten: Die angegebenen Wahrscheinlichkeiten sind auf vier Stellen gerundet  bzw.
bzw. 
Die Internetnutzung einer Person kann nicht gleichzeitig als problematisch und als Internetabhängigkeit eingestuft werden. Im Folgenden werden die in der PINTA-Studie ermittelten relativen Häufigkeiten bundesweit für alle Personen im Alter von
1.
Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:
- Eine zufällig ausgewählte männliche Person aus der Altersgruppe
-
wird als internetabhängig eingestuft.
- Unter
zufällig ausgewählten
-
-jährigen Mädchen sind genau
, deren Internetnutzung als problematisch eingestuft wird.
- Unter
zufällig gewählten
-
-jährigen Mädchen sind mehr als
, aber weniger als
, deren Internetnutzung als problematisch oder gar als Internetabhängigkeit eingestuft wird.
(7 BE)
2.
Im Internet finden sich zahlreiche Online-Tests, bei denen ein ähnlicher Fragenkatalog wie bei der Durchführung der PINTA-Studie zum Einsatz kommt. Hier können sich die Nutzer selbst bezüglich Internetabhängigkeit testen.
Die Wahrscheinlichkeit, dass ein bestimmter Online-Test einen tatsächlich internetabhängigen Nutzer auch als internetabhängig einstuft (Sensitivität), liegt bei . Für die Wahrscheinlichkeit, dass dieser Online-Test einen nicht internetabhängigen Nutzer auch als nicht internetabhängig einstuft (Spezifität), wird ein Wert von
. Für die Wahrscheinlichkeit, dass dieser Online-Test einen nicht internetabhängigen Nutzer auch als nicht internetabhängig einstuft (Spezifität), wird ein Wert von  angegeben. Eine zufällig ausgewählte Person aus der Altersgruppe
angegeben. Eine zufällig ausgewählte Person aus der Altersgruppe  -
- Jahre macht diesen Online-Test.
Jahre macht diesen Online-Test.
Die Wahrscheinlichkeit, dass ein bestimmter Online-Test einen tatsächlich internetabhängigen Nutzer auch als internetabhängig einstuft (Sensitivität), liegt bei
2.1
Berechne die Wahrscheinlichkeit für das Ereignis  „Wenn der Test die Person als internetabhängig einstuft, ist die Person auch tatsächlich internetabhängig.“
„Wenn der Test die Person als internetabhängig einstuft, ist die Person auch tatsächlich internetabhängig.“
(6 BE)
2.2
Die Wahrscheinlichkeit dafür, dass eine Person aus der Altersgruppe  -
- Jahre tatsächlich nicht internetabhängig ist, wenn der Test sie als nicht internetabhängig einstuft, beträgt ca.
Jahre tatsächlich nicht internetabhängig ist, wenn der Test sie als nicht internetabhängig einstuft, beträgt ca.  .
.
Beurteile die Qualität des Online-Tests anhand dieser und der in Aufgabe 2.1 berechneten Wahrscheinlichkeit.
Beurteile die Qualität des Online-Tests anhand dieser und der in Aufgabe 2.1 berechneten Wahrscheinlichkeit.
(2 BE)
3.
Aus dem Abschlussbericht zur PINTA-Studie geht hervor, dass von den 15023 befragten Personen  das Internet weniger als eine Stunde täglich privat nutzen. Dieser Personenkreis wird im Folgenden als „Wenignutzer“ bezeichnet.
Ein Mathematik-Leistungskurs an einer sehr großen Schule hat die Vermutung, dass der Anteil der Wenignutzer unter den Schülerinnen und Schülern der Schule niedriger ist als der in der PINTA-Studie ermittelte Wert. Der bevorstehende Tag der offenen Tür soll dazu genutzt werden, die Vermutung mit Hilfe eines Hypothesentests zu überprüfen. Hierzu sollen 100 zufällig ausgewählte Schülerinnen und Schüler der Schule befragt werden.
das Internet weniger als eine Stunde täglich privat nutzen. Dieser Personenkreis wird im Folgenden als „Wenignutzer“ bezeichnet.
Ein Mathematik-Leistungskurs an einer sehr großen Schule hat die Vermutung, dass der Anteil der Wenignutzer unter den Schülerinnen und Schülern der Schule niedriger ist als der in der PINTA-Studie ermittelte Wert. Der bevorstehende Tag der offenen Tür soll dazu genutzt werden, die Vermutung mit Hilfe eines Hypothesentests zu überprüfen. Hierzu sollen 100 zufällig ausgewählte Schülerinnen und Schüler der Schule befragt werden.
3.1
Entwickle zu der oben genannten Vermutung einen geeigneten Hypothesentest auf einem Signifikanzniveau von  und gib die Entscheidungsregel im Sachzusammenhang an.
und gib die Entscheidungsregel im Sachzusammenhang an.
(6 BE)
3.2
Beschreibe die Fehler 1. und 2. Art im Sachzusammenhang und berechnen Sie die Wahrscheinlichkeit für den Fehler 2. Art, wenn der Anteil der Wenignutzer unter den Schülerinnen und Schülern der Schule tatsächlich  beträgt.
beträgt.
(6 BE)
3.3
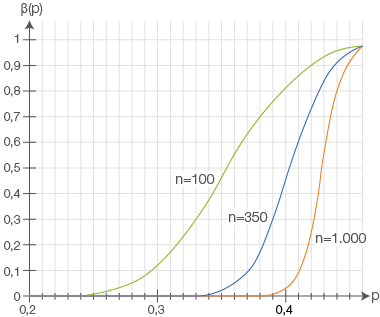
Die Graphen im Material zeigen für unterschiedliche Werte von  , wie sich bei einem gleich bleibenden Signifikanzniveau von
, wie sich bei einem gleich bleibenden Signifikanzniveau von  die Fehlerwahrscheinlichkeit
die Fehlerwahrscheinlichkeit  für den Fehler 2 . Art in Abhängigkeit vom tatsächlichen Anteil
für den Fehler 2 . Art in Abhängigkeit vom tatsächlichen Anteil  der Wenignutzer verhält.
der Wenignutzer verhält.
Beurteile anhand geeigneter Beispielwerte, ob sich eine Erhöhung des Stichprobenumfangs auf die Güte des Tests auswirkt.
auf die Güte des Tests auswirkt.
Material
Beurteile anhand geeigneter Beispielwerte, ob sich eine Erhöhung des Stichprobenumfangs
(3 BE)
1.
Wahrscheinlichkeiten bestimmen
Wahrscheinlichkeit für Ereignis  Die Wahrscheinlichkeit des Ereignisses
Die Wahrscheinlichkeit des Ereignisses  lässt sich aus der Tabelle ablesen.
lässt sich aus der Tabelle ablesen.  .
Wahrscheinlichkeit für Ereignis
.
Wahrscheinlichkeit für Ereignis  Hierbei ist
Hierbei ist  die Anzahl der 14-16-jährigen Mädchen, deren Internetnutzung als problematisch eingestuft wird.
die Anzahl der 14-16-jährigen Mädchen, deren Internetnutzung als problematisch eingestuft wird.  ist
ist  -verteilt. Unter 5: Wahrscheinlichkeit
-verteilt. Unter 5: Wahrscheinlichkeit  5: Verteilungen
5: Verteilungen  D: Binomial Pdf kann nun mit Hilfe des CAS
D: Binomial Pdf kann nun mit Hilfe des CAS  berechnet werden:
berechnet werden:



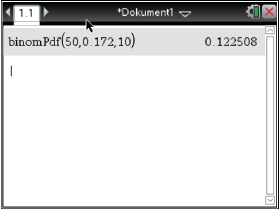 Somit tritt Ereignis
Somit tritt Ereignis  mit einer Wahrscheinlichkeit von ca.
mit einer Wahrscheinlichkeit von ca.  auf.
Wahrscheinlichkeit für Ereignis
auf.
Wahrscheinlichkeit für Ereignis  Bei Ereignis
Bei Ereignis  beschreibt
beschreibt  die Anzahl der
die Anzahl der  -jährigen Mädchen, deren Internetnutzung als problematisch oder gar als Internetabhängigkeit eingestuft wird. X ist binomial verteilt.
-jährigen Mädchen, deren Internetnutzung als problematisch oder gar als Internetabhängigkeit eingestuft wird. X ist binomial verteilt.

![\(\begin{array}[t]{rll}
p&=& p_{Abh} + p_{probl} \\[5pt]
&=& 0,049 + 0,172\\[5pt]
&=& 0,221
\end{array}\)](https://mathjax.schullv.de/5bd8e5ca433c3132ee172545f3bf70a4477815ae95403cc854d7a284aa70726c?color=5a5a5a) Mit Hilfe dieser Werte kann nun unter 5: Wahrscheinlichkeit
Mit Hilfe dieser Werte kann nun unter 5: Wahrscheinlichkeit  5: Verteilungen
5: Verteilungen  D: Binomial Cdf im CAS
D: Binomial Cdf im CAS 


 berechnet werden:
berechnet werden:

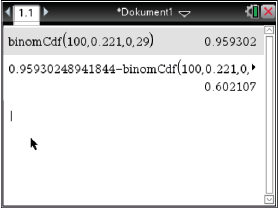 Somit tritt Ereignis
Somit tritt Ereignis  mit einer Wahrscheinlichkeit von
mit einer Wahrscheinlichkeit von  auf.
auf.


2.1
Wahrscheinlichkeit berechnen
Die Aufgabe lässt sich mit einer Vierfeldertafel lösen.
 : Person ist internetabhängig.
: Person ist internetabhängig.
 : Online-Test stuft Person als internetabhängig ein (Test positiv).
: Online-Test stuft Person als internetabhängig ein (Test positiv).


![\(\begin{array}[t]{rll}
P(\overline{A})&=& 1-P(A) \\[5pt]
&=& 1- 0,024\\[5pt]
&=& 0,976
\end{array}\)](https://mathjax.schullv.de/b6b798bf765be696ee6bbeb6ecd84cf8a0342a1b6748bbcee03c92f4d3c15c04?color=5a5a5a)
 In der Aufgabenstellung sind folgende Wahrscheinlichkeiten bereits gegeben :
In der Aufgabenstellung sind folgende Wahrscheinlichkeiten bereits gegeben :  und
und  Für eine bedingte Wahrscheinlichkeit gilt die Formel:
Für eine bedingte Wahrscheinlichkeit gilt die Formel:
 Somit kann nun die Wahrscheinlichkeiten
Somit kann nun die Wahrscheinlichkeiten  und
und  folgendermaßen bestimmt werden:
Für
folgendermaßen bestimmt werden:
Für  folgt entsprechend:
folgt entsprechend:
![\(\begin{array}[t]{rll}
P(\overline{A} \cap \overline{B})&=& P_{\overline{A}}(\overline{B}) \cdot P(\overline{A}) \\[5pt]
&=& 0,75 \cdot 0,976 \\[5pt]
&=& 0,7327
\end{array}\)](https://mathjax.schullv.de/f6d80bd4826f2ef4be6c220da2b30fbe273ef977e0e8c525e29965bfac76300a?color=5a5a5a) Nun kann die Vierfeldertafel erstellt werden:
Nun kann die Vierfeldertafel erstellt werden:
Schließlich kann  berechnet werden.
berechnet werden.




2.2
Qualität des Tests beurteilen
Die Wahrscheinlichkeit  erscheint mit ca.
erscheint mit ca.  sehr gering. Bei einem positiven Testergebnis sind also weitere Untersuchungen ratsam. Die in Aufgabe
sehr gering. Bei einem positiven Testergebnis sind also weitere Untersuchungen ratsam. Die in Aufgabe  angegebene Wahrscheinlichkeit ist mit
angegebene Wahrscheinlichkeit ist mit  sehr hoch. Personen, die ein negatives Testergebnis erhalten, können also mit hoher Wahrscheinlichkeit davon ausgehen, dass sie tatsächlich nicht internetabhängig sind. Deshalb ist der Online-Test gut geeignet, um eine Internetabhängigkeit auszuschließen.
sehr hoch. Personen, die ein negatives Testergebnis erhalten, können also mit hoher Wahrscheinlichkeit davon ausgehen, dass sie tatsächlich nicht internetabhängig sind. Deshalb ist der Online-Test gut geeignet, um eine Internetabhängigkeit auszuschließen.
3.1
Hypothesentest entwickeln und Entscheidungsregel im Sachzusammenhang angeben
 : Anzahl der Schüler, die zur Gruppe der Wenignutzer gehören
: Anzahl der Schüler, die zur Gruppe der Wenignutzer gehören
 = 100
Die Nullhypothese
= 100
Die Nullhypothese  und die Alternativhypothese
und die Alternativhypothese  können nun wie folgt formuliert werden:
können nun wie folgt formuliert werden:

 In Worten lautet die Nullhypothese: Es sind mindestens
In Worten lautet die Nullhypothese: Es sind mindestens  der Schüler Wenignutzer.
Das heißt, es wird ein linksseitiger Hypothesentest durchgeführt. Der Ablehnungsbereich
der Schüler Wenignutzer.
Das heißt, es wird ein linksseitiger Hypothesentest durchgeführt. Der Ablehnungsbereich  lautet:
lautet:
 Deshalb muss gelten:
Deshalb muss gelten:
 Aus der Tabelle folgt:
Aus der Tabelle folgt:
 und
und  .
Somit folgt für den Ablehungsbereich:
.
Somit folgt für den Ablehungsbereich:
 Das bedeutet, dass wenn
Das bedeutet, dass wenn  oder weniger der befragten Nutzer zu der Gruppe der Wenignutzer gehören wird die Nullhypothese verworfen und somit wird die Vermutung des Mathematik-Leisungskurs als bestätigt betrachtet.
oder weniger der befragten Nutzer zu der Gruppe der Wenignutzer gehören wird die Nullhypothese verworfen und somit wird die Vermutung des Mathematik-Leisungskurs als bestätigt betrachtet.
3.2
Fehler 1. und 2. Art beschreiben
Der Fehler 1. Art beschreibt, dass die Nullhypothese abgelehnt wird, obwohl diese in Wahrheit zutrifft. Im Sachzusammenhang bedeutet dies, dass man aufgrund des Hypothesentests davon ausgeht, dass der Anteil der Wenignutzer geringer als  ist, also dass die Nullhypothese abgelehnt wird, obwohl der Anteil in Wahrheit
ist, also dass die Nullhypothese abgelehnt wird, obwohl der Anteil in Wahrheit  oder mehr beträgt.
Der Fehler 2. Art beschreibt, dass die Nullhypothese angenommen wird, obwohl diese in Wahrheit nicht zutrifft. Im Sachzusammenhang bedeutet dies, dass man aufgrund des Hypothesentests davon ausgeht, dass der Anteil der Wenignutzer gleich oder größer als
oder mehr beträgt.
Der Fehler 2. Art beschreibt, dass die Nullhypothese angenommen wird, obwohl diese in Wahrheit nicht zutrifft. Im Sachzusammenhang bedeutet dies, dass man aufgrund des Hypothesentests davon ausgeht, dass der Anteil der Wenignutzer gleich oder größer als  ist, also dass die Nullhypothese angenommen wird, obwohl der Anteil in Wahrheit kleiner als
ist, also dass die Nullhypothese angenommen wird, obwohl der Anteil in Wahrheit kleiner als  ist.
Wahrscheinlichkeit für den Fehler 2.Art bestimmen:
Es wird die Wahrscheinlichkeit berechnet, dass
ist.
Wahrscheinlichkeit für den Fehler 2.Art bestimmen:
Es wird die Wahrscheinlichkeit berechnet, dass  im Annahmebereich liegt mit
im Annahmebereich liegt mit 
 .
Somit berechnet sich die Wahrscheinlichkeit für einen Fehler 2. Art wie folgt:
.
Somit berechnet sich die Wahrscheinlichkeit für einen Fehler 2. Art wie folgt:


 Mit Hilfe des CAS folgt dann weiter:
Mit Hilfe des CAS folgt dann weiter:



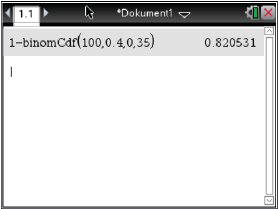 Somit beträgt die Wahrscheinlichkeit für einen Fehler 2. Art
Somit beträgt die Wahrscheinlichkeit für einen Fehler 2. Art  .
.

3.3
Güte des Tests beurteilen
Die Kurven werden mit wachsendem  immer steiler. Die Betrachtung von
immer steiler. Die Betrachtung von  (p) für verschiedene
(p) für verschiedene  bei einem festen Wert
bei einem festen Wert  , beispielsweise
, beispielsweise  , zeigt: Für
, zeigt: Für  ergibt sich der Wert
ergibt sich der Wert  , für
, für  der Wert
der Wert  und für
und für  der Wert
der Wert  . Je größer
. Je größer  ist, desto kleiner ist also
ist, desto kleiner ist also  , d.h. desto kleiner ist die Wahrscheinlichkeit für einen Fehler 2. Art. Eine Erhöhung des Stichprobenumfangs
, d.h. desto kleiner ist die Wahrscheinlichkeit für einen Fehler 2. Art. Eine Erhöhung des Stichprobenumfangs  wirkt sich somit positiv auf die Güte des Tests aus.
wirkt sich somit positiv auf die Güte des Tests aus.
1.
Wahrscheinlichkeiten bestimmen
Wahrscheinlichkeit für Ereignis  Die Wahrscheinlichkeit des Ereignisses
Die Wahrscheinlichkeit des Ereignisses  lässt sich aus der Tabelle ablesen.
lässt sich aus der Tabelle ablesen.  .
Wahrscheinlichkeit für Ereignis
.
Wahrscheinlichkeit für Ereignis  Hierbei ist
Hierbei ist  die Anzahl der 14-16-jährigen Mädchen, deren Internetnutzung als problematisch eingestuft wird.
die Anzahl der 14-16-jährigen Mädchen, deren Internetnutzung als problematisch eingestuft wird.  ist
ist  -verteilt. Unter 5: Wahrscheinlichkeit
-verteilt. Unter 5: Wahrscheinlichkeit  5: Verteilungen
5: Verteilungen  D: Binomial Pdf kann nun mit Hilfe des CAS
D: Binomial Pdf kann nun mit Hilfe des CAS  berechnet werden:
berechnet werden:



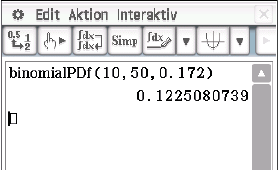 Somit tritt Ereignis
Somit tritt Ereignis  mit einer Wahrscheinlichkeit von ca.
mit einer Wahrscheinlichkeit von ca.  auf.
Wahrscheinlichkeit für Ereignis
auf.
Wahrscheinlichkeit für Ereignis  Bei Ereignis
Bei Ereignis  beschreibt
beschreibt  die Anzahl der
die Anzahl der  -jährigen Mädchen, deren Internetnutzung als problematisch oder gar als Internetabhängigkeit eingestuft wird. X ist binomial verteilt.
-jährigen Mädchen, deren Internetnutzung als problematisch oder gar als Internetabhängigkeit eingestuft wird. X ist binomial verteilt.

![\(\begin{array}[t]{rll}
p&=& p_{Abh} + p_{probl} \\[5pt]
&=& 0,049 + 0,172\\[5pt]
&=& 0,221
\end{array}\)](https://mathjax.schullv.de/5bd8e5ca433c3132ee172545f3bf70a4477815ae95403cc854d7a284aa70726c?color=5a5a5a) Mit Hilfe dieser Werte kann nun unter 5: Wahrscheinlichkeit
Mit Hilfe dieser Werte kann nun unter 5: Wahrscheinlichkeit  5: Verteilungen
5: Verteilungen  D: Binomial Cdf im CAS
D: Binomial Cdf im CAS 


 berechnet werden:
berechnet werden:

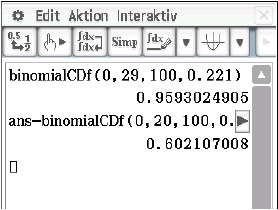 Somit tritt Ereignis
Somit tritt Ereignis  mit einer Wahrscheinlichkeit von
mit einer Wahrscheinlichkeit von  auf.
auf.


2.1
Wahrscheinlichkeit berechnen
Die Aufgabe lässt sich mit einer Vierfeldertafel lösen.
 : Person ist internetabhängig.
: Person ist internetabhängig.
 : Online-Test stuft Person als internetabhängig ein (Test positiv).
: Online-Test stuft Person als internetabhängig ein (Test positiv).


![\(\begin{array}[t]{rll}
P(\overline{A})&=& 1-P(A) \\[5pt]
&=& 1- 0,024\\[5pt]
&=& 0,976
\end{array}\)](https://mathjax.schullv.de/b6b798bf765be696ee6bbeb6ecd84cf8a0342a1b6748bbcee03c92f4d3c15c04?color=5a5a5a)
 In der Aufgabenstellung sind folgende Wahrscheinlichkeiten bereits gegeben :
In der Aufgabenstellung sind folgende Wahrscheinlichkeiten bereits gegeben :  und
und  Für eine bedingte Wahrscheinlichkeit gilt die Formel:
Für eine bedingte Wahrscheinlichkeit gilt die Formel:
 Somit kann nun die Wahrscheinlichkeiten
Somit kann nun die Wahrscheinlichkeiten  und
und  folgendermaßen bestimmt werden:
Für
folgendermaßen bestimmt werden:
Für  folgt entsprechend:
folgt entsprechend:
![\(\begin{array}[t]{rll}
P(\overline{A} \cap \overline{B})&=& P_{\overline{A}}(\overline{B}) \cdot P(\overline{A}) \\[5pt]
&=& 0,75 \cdot 0,976 \\[5pt]
&=& 0,7327
\end{array}\)](https://mathjax.schullv.de/f6d80bd4826f2ef4be6c220da2b30fbe273ef977e0e8c525e29965bfac76300a?color=5a5a5a) Nun kann die Vierfeldertafel erstellt werden:
Nun kann die Vierfeldertafel erstellt werden:
Schließlich kann  berechnet werden.
berechnet werden.




2.2
Qualität des Tests beurteilen
Die Wahrscheinlichkeit  erscheint mit ca.
erscheint mit ca.  sehr gering. Bei einem positiven Testergebnis sind also weitere Untersuchungen ratsam. Die in Aufgabe
sehr gering. Bei einem positiven Testergebnis sind also weitere Untersuchungen ratsam. Die in Aufgabe  angegebene Wahrscheinlichkeit ist mit
angegebene Wahrscheinlichkeit ist mit  sehr hoch. Personen, die ein negatives Testergebnis erhalten, können also mit hoher Wahrscheinlichkeit davon ausgehen, dass sie tatsächlich nicht internetabhängig sind. Deshalb ist der Online-Test gut geeignet, um eine Internetabhängigkeit auszuschließen.
sehr hoch. Personen, die ein negatives Testergebnis erhalten, können also mit hoher Wahrscheinlichkeit davon ausgehen, dass sie tatsächlich nicht internetabhängig sind. Deshalb ist der Online-Test gut geeignet, um eine Internetabhängigkeit auszuschließen.
3.1
Hypothesentest entwickeln und Entscheidungsregel im Sachzusammenhang angeben
 : Anzahl der Schüler, die zur Gruppe der Wenignutzer gehören
: Anzahl der Schüler, die zur Gruppe der Wenignutzer gehören
 = 100
Die Nullhypothese
= 100
Die Nullhypothese  und die Alternativhypothese
und die Alternativhypothese  können nun wie folgt formuliert werden:
können nun wie folgt formuliert werden:

 In Worten lautet die Nullhypothese: Es sind mindestens
In Worten lautet die Nullhypothese: Es sind mindestens  der Schüler Wenignutzer.
Das heißt, es wird ein linksseitiger Hypothesentest durchgeführt. Der Ablehnungsbereich
der Schüler Wenignutzer.
Das heißt, es wird ein linksseitiger Hypothesentest durchgeführt. Der Ablehnungsbereich  lautet:
lautet:
 Deshalb muss gelten:
Deshalb muss gelten:
 Aus der Tabelle folgt:
Aus der Tabelle folgt:
 und
und  .
Somit folgt für den Ablehungsbereich:
.
Somit folgt für den Ablehungsbereich:
 Das bedeutet, dass wenn
Das bedeutet, dass wenn  oder weniger der befragten Nutzer zu der Gruppe der Wenignutzer gehören wird die Nullhypothese verworfen und somit wird die Vermutung des Mathematik-Leisungskurs als bestätigt betrachtet.
oder weniger der befragten Nutzer zu der Gruppe der Wenignutzer gehören wird die Nullhypothese verworfen und somit wird die Vermutung des Mathematik-Leisungskurs als bestätigt betrachtet.
3.2
Fehler 1. und 2. Art beschreiben
Der Fehler 1. Art beschreibt, dass die Nullhypothese abgelehnt wird, obwohl diese in Wahrheit zutrifft. Im Sachzusammenhang bedeutet dies, dass man aufgrund des Hypothesentests davon ausgeht, dass der Anteil der Wenignutzer geringer als  ist, also dass die Nullhypothese abgelehnt wird, obwohl der Anteil in Wahrheit
ist, also dass die Nullhypothese abgelehnt wird, obwohl der Anteil in Wahrheit  oder mehr beträgt.
Der Fehler 2. Art beschreibt, dass die Nullhypothese angenommen wird, obwohl diese in Wahrheit nicht zutrifft. Im Sachzusammenhang bedeutet dies, dass man aufgrund des Hypothesentests davon ausgeht, dass der Anteil der Wenignutzer gleich oder größer als
oder mehr beträgt.
Der Fehler 2. Art beschreibt, dass die Nullhypothese angenommen wird, obwohl diese in Wahrheit nicht zutrifft. Im Sachzusammenhang bedeutet dies, dass man aufgrund des Hypothesentests davon ausgeht, dass der Anteil der Wenignutzer gleich oder größer als  ist, also dass die Nullhypothese angenommen wird, obwohl der Anteil in Wahrheit kleiner als
ist, also dass die Nullhypothese angenommen wird, obwohl der Anteil in Wahrheit kleiner als  ist.
Wahrscheinlichkeit für den Fehler 2.Art bestimmen:
Es wird die Wahrscheinlichkeit berechnet, dass
ist.
Wahrscheinlichkeit für den Fehler 2.Art bestimmen:
Es wird die Wahrscheinlichkeit berechnet, dass  im Annahmebereich liegt mit
im Annahmebereich liegt mit 
 .
Somit berechnet sich die Wahrscheinlichkeit für einen Fehler 2. Art wie folgt:
.
Somit berechnet sich die Wahrscheinlichkeit für einen Fehler 2. Art wie folgt:


 Mit Hilfe des CAS folgt dann weiter:
Mit Hilfe des CAS folgt dann weiter:



 Somit beträgt die Wahrscheinlichkeit für einen Fehler 2. Art
Somit beträgt die Wahrscheinlichkeit für einen Fehler 2. Art  .
.

3.3
Güte des Tests beurteilen
Die Kurven werden mit wachsendem  immer steiler. Die Betrachtung von
immer steiler. Die Betrachtung von  (p) für verschiedene
(p) für verschiedene  bei einem festen Wert
bei einem festen Wert  , beispielsweise
, beispielsweise  , zeigt: Für
, zeigt: Für  ergibt sich der Wert
ergibt sich der Wert  , für
, für  der Wert
der Wert  und für
und für  der Wert
der Wert  . Je größer
. Je größer  ist, desto kleiner ist also
ist, desto kleiner ist also  , d.h. desto kleiner ist die Wahrscheinlichkeit für einen Fehler 2. Art. Eine Erhöhung des Stichprobenumfangs
, d.h. desto kleiner ist die Wahrscheinlichkeit für einen Fehler 2. Art. Eine Erhöhung des Stichprobenumfangs  wirkt sich somit positiv auf die Güte des Tests aus.
wirkt sich somit positiv auf die Güte des Tests aus.