B2 - Analysis
1
Gegeben ist die Funktionenschar  mit
mit 

1.1
Berechne die Extrempunkte des Graphen von  und gib die verwendeten Ableitungsregeln an. Dabei darf die zweite Ableitung
ohne Nachweis verwendet werden.
und gib die verwendeten Ableitungsregeln an. Dabei darf die zweite Ableitung
ohne Nachweis verwendet werden.
(11 BE)
1.2
Der Hochpunkt des Graphen von  hat die Koordinaten
hat die Koordinaten  Begründe, dass für einen festen Wert von
Begründe, dass für einen festen Wert von  alle Hochpunkte auf einer Parallelen zur
alle Hochpunkte auf einer Parallelen zur  -Achse liegen.
-Achse liegen.
Für einen festen Wert von liegen alle Hochpunkte auf einer Parabel mit der Gleichung
liegen alle Hochpunkte auf einer Parabel mit der Gleichung  Leite diese Gleichung her und skizziere die Parabel für
Leite diese Gleichung her und skizziere die Parabel für  in der Abbildung in Material 1.
in der Abbildung in Material 1.

Für einen festen Wert von
(6 BE)

Material 1: Funktionenschar
1.3
Bestimme die Werte der Parameter  und
und  für diejenige Funktion der Schar
für diejenige Funktion der Schar  die an der Stelle
die an der Stelle  den Funktionswert
den Funktionswert  und an der Stelle
und an der Stelle  den Funktionswert
den Funktionswert  annimmt.
annimmt.
(3 BE)
2
Ein Sportartikelhersteller bringt ein neues Modell eines Laufschuhs auf den Markt. Die Wochen nach Verkaufsstart werden durchnummeriert und es wird für jede Woche die Anzahl der verkauften Paare des neuen Modells ermittelt. Seit Verkaufsstart sind  Wochen vergangen. Die Kreuze in Material 2 zeigen die Verkaufszahlen für den genannten Zeitraum.
Wochen vergangen. Die Kreuze in Material 2 zeigen die Verkaufszahlen für den genannten Zeitraum.
Eine gute Modellierung des Verlaufs der Verkaufszahlen liefert die Scharfunktion mit
mit  deren Graphen in Material 3 eingezeichnet ist.
deren Graphen in Material 3 eingezeichnet ist.
Nach den ersten Wochen liegen insgesamt noch etwa
Wochen liegen insgesamt noch etwa  Schuhpaare des neuen Modells auf Lager und der Hersteller möchte wissen, ob diese reichen werden, oder ob weitere Schuhe produziert werden müssen. Um diese Frage zu beantworten, soll eine auf der Integralrechnung basierende Methode entwickelt werden, die es ermöglicht, die Verkaufszahlen näherungsweise zu berechnen und Prognosen für die Zukunft zu erstellen.
Schuhpaare des neuen Modells auf Lager und der Hersteller möchte wissen, ob diese reichen werden, oder ob weitere Schuhe produziert werden müssen. Um diese Frage zu beantworten, soll eine auf der Integralrechnung basierende Methode entwickelt werden, die es ermöglicht, die Verkaufszahlen näherungsweise zu berechnen und Prognosen für die Zukunft zu erstellen.


Eine gute Modellierung des Verlaufs der Verkaufszahlen liefert die Scharfunktion
Nach den ersten

Material 2: Verkaufszahlen in den ersten  Wochen
Wochen

Material 3: Modellierung der Verkaufszahlen mit der Funktion 
2.1
In der 1. Woche wurden  , in der 2. Woche
, in der 2. Woche  , in der 3. Woche
, in der 3. Woche  und der 4. Woche
und der 4. Woche  Schuhpaare des neuen Modells verkauft, also
Schuhpaare des neuen Modells verkauft, also  Schuhpaare insgesamt.
Schuhpaare insgesamt.
Hierfür liefert die Summe
 einen guten Näherungswert. Bestimme diese Summe und zeige, dass die prozentuale Abweichung dieses Näherungswertes von der tatsächlichen Verkaufszahl weniger als
einen guten Näherungswert. Bestimme diese Summe und zeige, dass die prozentuale Abweichung dieses Näherungswertes von der tatsächlichen Verkaufszahl weniger als  beträgt.
beträgt.
Hierfür liefert die Summe
(3 BE)
2.2
Die Summe der vier Funktionswerte aus Aufgabe 2.1 lässt sich als Gesamtflächeninhalt von vier Rechtecken darstellen. Diese vier Rechtecke sind in den Abbildungen  und
und  in Material 4 jeweils zusammen mit dem Graphen der Funktion
in Material 4 jeweils zusammen mit dem Graphen der Funktion  dargestellt.
dargestellt.
Der Flächeninhalt der vier Rechtecke - und somit auch die Anzahl der in den ersten vier Wochen verkauften Schuhpaare - lässt sich durch den Inhalt einer Fläche unter dem Graphen von sehr gut approximieren.
sehr gut approximieren.

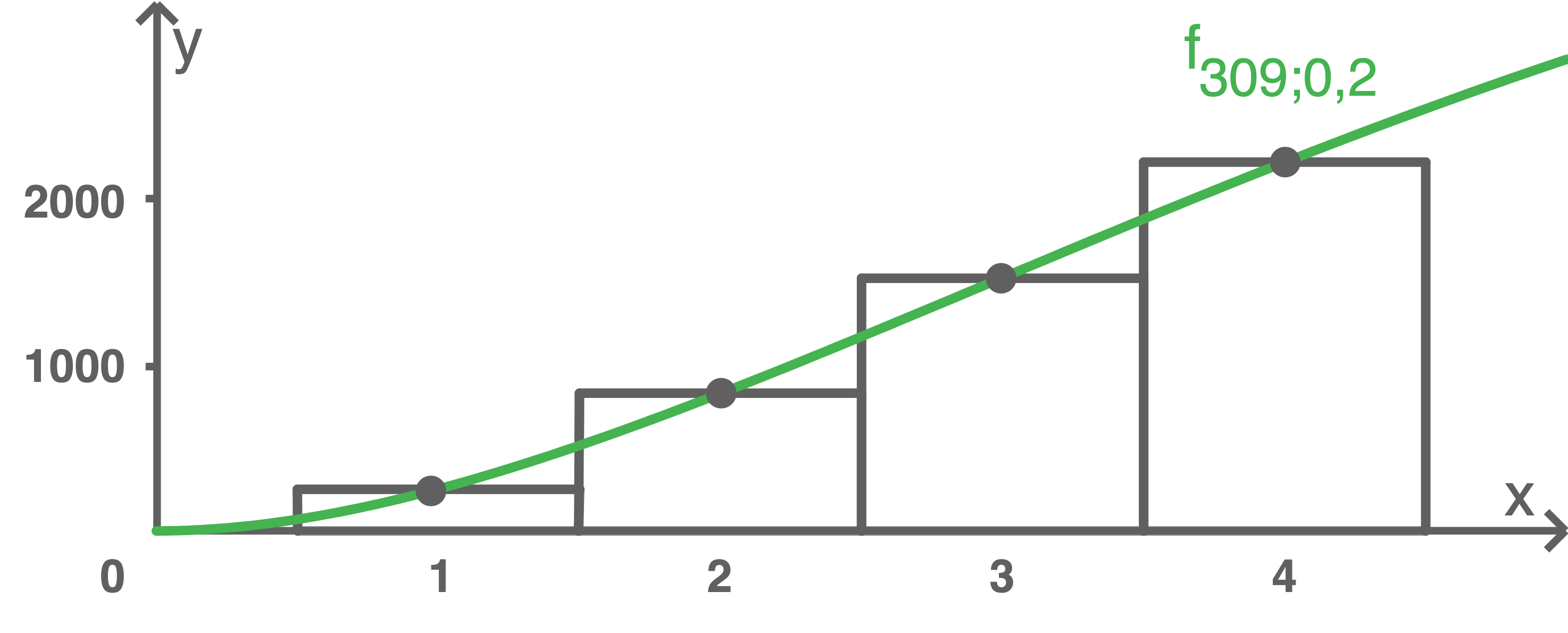
Der Flächeninhalt der vier Rechtecke - und somit auch die Anzahl der in den ersten vier Wochen verkauften Schuhpaare - lässt sich durch den Inhalt einer Fläche unter dem Graphen von

Abbildung A

Abbildung B
Material 4: Darstellung der Funktionswerte von  als Rechteckflächen
als Rechteckflächen
2.2.1
Bestimme (mit Hilfe des CAS) die Werte der beiden Integrale  und
und 
(2 BE)
2.2.2
Begründe anschaulich mithilfe von Material 4, warum das Integral  eine sehr gute, das Integral
eine sehr gute, das Integral  hingegen eine weniger gute Approximation für die Summe der Flächeninhalte der Rechtecke darstellt.
hingegen eine weniger gute Approximation für die Summe der Flächeninhalte der Rechtecke darstellt.
(3 BE)
2.3
Bestimme die kleinste natürliche Zahl  für die
für die  gilt, und deute das Ergebnis im Sachzusammenhang.
gilt, und deute das Ergebnis im Sachzusammenhang.
(5 BE)
2.4
Bestimme den Grenzwert  und deute das Ergebnis im Sachzusammenhang unter Berücksichtigung der vom Sportartikelhersteller aufgeworfenen Frage.
und deute das Ergebnis im Sachzusammenhang unter Berücksichtigung der vom Sportartikelhersteller aufgeworfenen Frage.
(4 BE)
3
Ein Sommerschuh wird seit vielen Jahren erfolgreich verkauft, wobei die Verkaufszahlen saisonalen Schwankungen unterliegen. Die Wochen nach dem Verkaufsstart des Schuhs werden analog zu Aufgabe 2 durchnummeriert. Am Ende jeder Woche wird die Gesamtzahl der bis dahin verkauften Schuhpaare ermittelt.
Die Gesamtverkaufszahlen für den Sommerschuh werden in sehr guter Näherung durch die Funktion mit
mit  modelliert, deren Graph in Material 5 dargestellt ist.
Material 5
modelliert, deren Graph in Material 5 dargestellt ist.
Material 5
Gesamtverkaufszahlen des Sommerschuhs seit Verkaufsstart
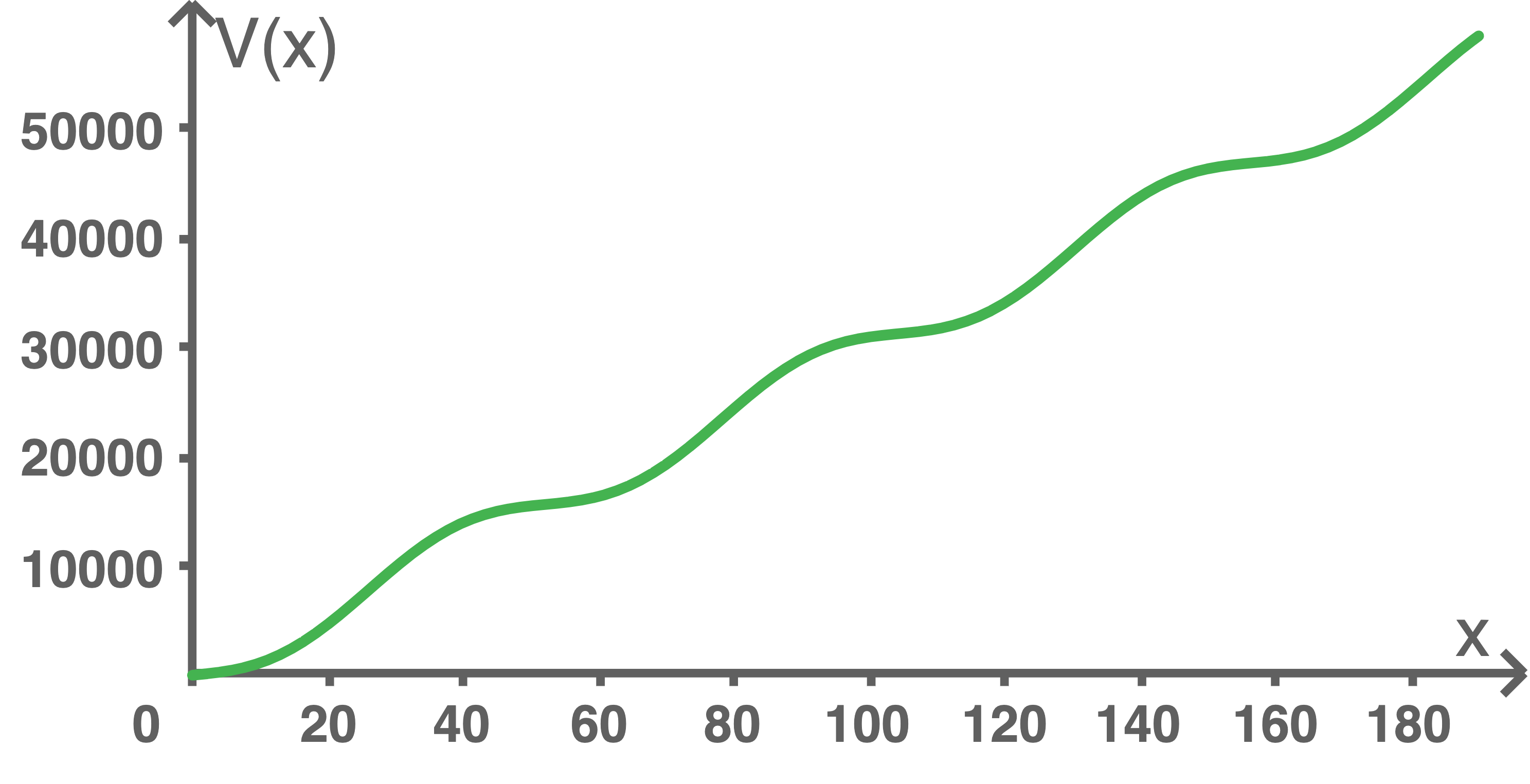
Die Gesamtverkaufszahlen für den Sommerschuh werden in sehr guter Näherung durch die Funktion
Gesamtverkaufszahlen des Sommerschuhs seit Verkaufsstart

Material 5: Gesamtverkaufszahlen des Sommerschuhs seit Verkaufsstart
3.1
In einer Sonderaktion erhält der Käufer des zehntausendsten Schuhpaars einen Bonus-Gutschein. Ermittle, in der wievielten Woche dieser Preis vergeben wird.
(3 BE)
3.2
Berechne die Funktionsgleichung der Ableitungsfunktion 
Begründe, dass gilt, und erläutere die Bedeutung der Grenzen
gilt, und erläutere die Bedeutung der Grenzen  und
und  des Wertebereiches von
des Wertebereiches von  im Sachzusammenhang.
im Sachzusammenhang.
Begründe, dass
(6 BE)
3.3
Bestimme den Grenzwert  und deute das Ergebnis im Sachzusammenhang.
und deute das Ergebnis im Sachzusammenhang.
(4BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
1. Schritt: Ableitung berechnen
 Für die erste Ableitung wird zunächst die Produktregel angewandt. Zur Ableitung des Terms
Für die erste Ableitung wird zunächst die Produktregel angewandt. Zur Ableitung des Terms  wird dann die Kettenregel angewandt:
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
wird dann die Kettenregel angewandt:
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f_{a;k}](https://mathjax.schullv.de/f338ec190421731f0a992208025532bad053118ffc6e93941f8d26764c68d2cd?color=5a5a5a) Wegen
Wegen  und
und  muss
muss  gelten. Nach dem Satz vom Nullprodukt gilt
gelten. Nach dem Satz vom Nullprodukt gilt  oder
oder  Durch Umstellen folgt
Durch Umstellen folgt  3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

 Es gilt
Es gilt  und
und  Damit liegt bei
Damit liegt bei  ein Tiefpunkt und bei
ein Tiefpunkt und bei  ein Hochpunkt vor.
ein Hochpunkt vor.
1.2
Hochpunkte für festes  Die
Die  Koordinate des Hochpunkts von
Koordinate des Hochpunkts von  ist fest, da sie nur von
ist fest, da sie nur von  abhängt. Da die
abhängt. Da die  Koordinate außerdem von
Koordinate außerdem von  abhängt, verschieben sich die Hochpunkte parallel zur
abhängt, verschieben sich die Hochpunkte parallel zur  -Achse. Also liegen alle Hochpunkte auf einer zur
-Achse. Also liegen alle Hochpunkte auf einer zur  -Achse parallelen Gerade.
Ortskurve für festes
-Achse parallelen Gerade.
Ortskurve für festes 
 wird nach
wird nach  umgestellt:
umgestellt:
![\(\begin{array}[t]{rll}
x&=& \dfrac{2}{k}& \quad \mid\,\cdot k \scriptsize \\[5pt]
x\cdot k&=& 2 & \quad \mid\,:x\scriptsize \\[5pt]
k &=& \dfrac{2}{x}& \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f99a387402bb6097bfbdb7f829248e0164be1536e6e99accda9f6a1dd7271b9a?color=5a5a5a) Einsetzen in die
Einsetzen in die  Koordinate:
Damit liegen alle Hochpunkte auf der angegebenen Parabel
Koordinate:
Damit liegen alle Hochpunkte auf der angegebenen Parabel 
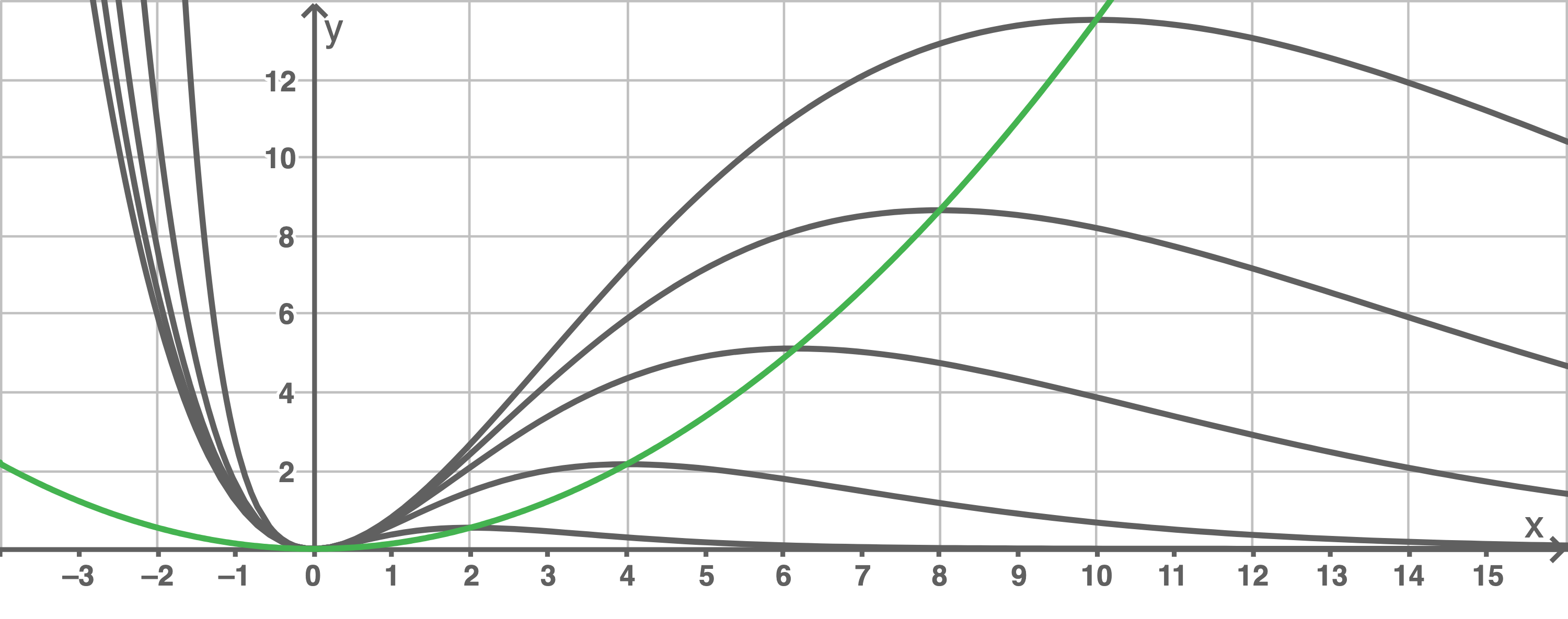

Material 1: Funktionenschar und Ortskurve
1.3
Es gilt:  und
und  Die Parameter
Die Parameter  und
und  lassen sich durch ein Gleichungssystem mit dem CAS bestimmen:
lassen sich durch ein Gleichungssystem mit dem CAS bestimmen:

 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Die Werte
Casio Classpad II
Die Werte  und
und  erfüllen die Gleichungen.
erfüllen die Gleichungen.
menu  3: Algebra
3: Algebra  7
7
keyboard  Math1
Math1 

2.1
1. Schritt: Summe berechnen
2. Schritt: Prozentuale Abweichung berechnen
 Somit beträgt die prozentuale Abweichung des Näherungswertes von der tatsächlichen Verkaufszahl ungefähr
Somit beträgt die prozentuale Abweichung des Näherungswertes von der tatsächlichen Verkaufszahl ungefähr  und damit weniger als
und damit weniger als  .
.
2.2.1
Die Integrale können mit dem CAS gelöst werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II


menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

2.2.2
In Abbildung A werden die Rechtecke im Intervall ![\([0;4]\)](https://mathjax.schullv.de/1560f98ba45b1bf50e4254268fc3492c704d99f31b7a236afb4a70174b7d628e?color=5a5a5a) dargestellt. Hier wird der Flächeninhalt der Rechtecke also durch das Integral
dargestellt. Hier wird der Flächeninhalt der Rechtecke also durch das Integral  approximiert. Entsprechend wird in Abbildung B der Flächeninhalt der Rechtecke durch das Integral
approximiert. Entsprechend wird in Abbildung B der Flächeninhalt der Rechtecke durch das Integral  approximiert.
In Abbildung A ist der Flächeninhalt der Fläche der Rechtecke deutlich größer als der Flächeninhalt der Fläche, die der Graph von
approximiert.
In Abbildung A ist der Flächeninhalt der Fläche der Rechtecke deutlich größer als der Flächeninhalt der Fläche, die der Graph von  im Intervall
im Intervall ![\([0;4]\)](https://mathjax.schullv.de/1560f98ba45b1bf50e4254268fc3492c704d99f31b7a236afb4a70174b7d628e?color=5a5a5a) mit der
mit der  -Achse einschließt. Somit ist das Integral
-Achse einschließt. Somit ist das Integral  eine weniger gute Approximation für die Summe der Flächeninhalte der Rechtecke.
Mit Abbildung B lässt sich erkennen, dass der Teil der Rechtecke, der über dem Graphen von
eine weniger gute Approximation für die Summe der Flächeninhalte der Rechtecke.
Mit Abbildung B lässt sich erkennen, dass der Teil der Rechtecke, der über dem Graphen von  liegt, ungefähr so groß ist wie der Flächeninhalt der Fläche unter dem Graphen, der nicht in den Rechtecken enthalten ist. Somit gleichen sich diese Flächen aus und das Integral
liegt, ungefähr so groß ist wie der Flächeninhalt der Fläche unter dem Graphen, der nicht in den Rechtecken enthalten ist. Somit gleichen sich diese Flächen aus und das Integral  liefert eine gute Approximation für die Summe der Flächeninhalte der Rechtecke.
liefert eine gute Approximation für die Summe der Flächeninhalte der Rechtecke.
2.3
Mit dem solve-Befehl des CAS ergibt sich für  die Lösung
die Lösung  Die kleinste natürliche Zahl, für die
Die kleinste natürliche Zahl, für die  gilt, ist somit
gilt, ist somit  Im Sachzusammenhang bedeutet dies, dass im Zeitraum von der 14. Woche bis zur 21. Woche mehr als
Im Sachzusammenhang bedeutet dies, dass im Zeitraum von der 14. Woche bis zur 21. Woche mehr als  Schuhe verkauft werden.
Schuhe verkauft werden.
2.4
Der CAS liefert:
 Im Sachzusammenhang bedeutet dies, dass nach der
Im Sachzusammenhang bedeutet dies, dass nach der  Woche noch etwa
Woche noch etwa  Schuhe verkauft werden. Die
Schuhe verkauft werden. Die  Schuhe, die noch auf Lager liegen, werden also ausreichen.
Schuhe, die noch auf Lager liegen, werden also ausreichen.
3.1
Es muss gelten:
Mit dem solve-Befehl des CAS gilt  Damit wird der Preis in der
Damit wird der Preis in der  Woche vergeben.
Woche vergeben.
3.2
Ableitung bestimmen
Mit der Kettenregel gilt:
Wertebereich begründen
Die Kosinus-Funktion nimmt Werte zwischen  und
und  an. Es müssen die
an. Es müssen die  -Werte bestimmt werden, für die
-Werte bestimmt werden, für die  und
und  gilt.
Für
gilt.
Für  gilt
gilt  und für
und für  gilt
gilt  Einsetzen von
Einsetzen von  und
und  in die Ableitungsfunktion ergibt:
in die Ableitungsfunktion ergibt:
 Damit wird ersichtlich, dass
Damit wird ersichtlich, dass  gilt.
Bedeutung im Sachzusammenhang
Die Verkaufszahlen der Schuhpaare schwanken folglich in der Woche periodisch zwischen
gilt.
Bedeutung im Sachzusammenhang
Die Verkaufszahlen der Schuhpaare schwanken folglich in der Woche periodisch zwischen  und
und  .
.
3.3
Im Sachzusammenhang bedeutet das Ergebnis, dass durchschnittlich 300 Schuhpaare pro Monat verkauft werden.