C1 - Lineare Algebra/ Analytische Geometrie
Für eine Kirmes soll in einem Dorf ein Festzelt errichtet werden, das aus einem quaderförmigen Unterbau und einem symmetrischen Dach in Form eines dreieckigen Prismas besteht.
Im Modell sind die Eckpunkte 


 des Unterbaus und der Endpunkt
des Unterbaus und der Endpunkt  der waagrecht verlaufenden Dachkante
der waagrecht verlaufenden Dachkante  vorgegeben.
Die durch die Punkte
vorgegeben.
Die durch die Punkte  begrenzte Vorderseite des Festzelts liegt in einer Ebene. Der Erdboden liegt in der
begrenzte Vorderseite des Festzelts liegt in einer Ebene. Der Erdboden liegt in der  -Ebene. Alle Einheiten sind in Meter angegeben.
-Ebene. Alle Einheiten sind in Meter angegeben.
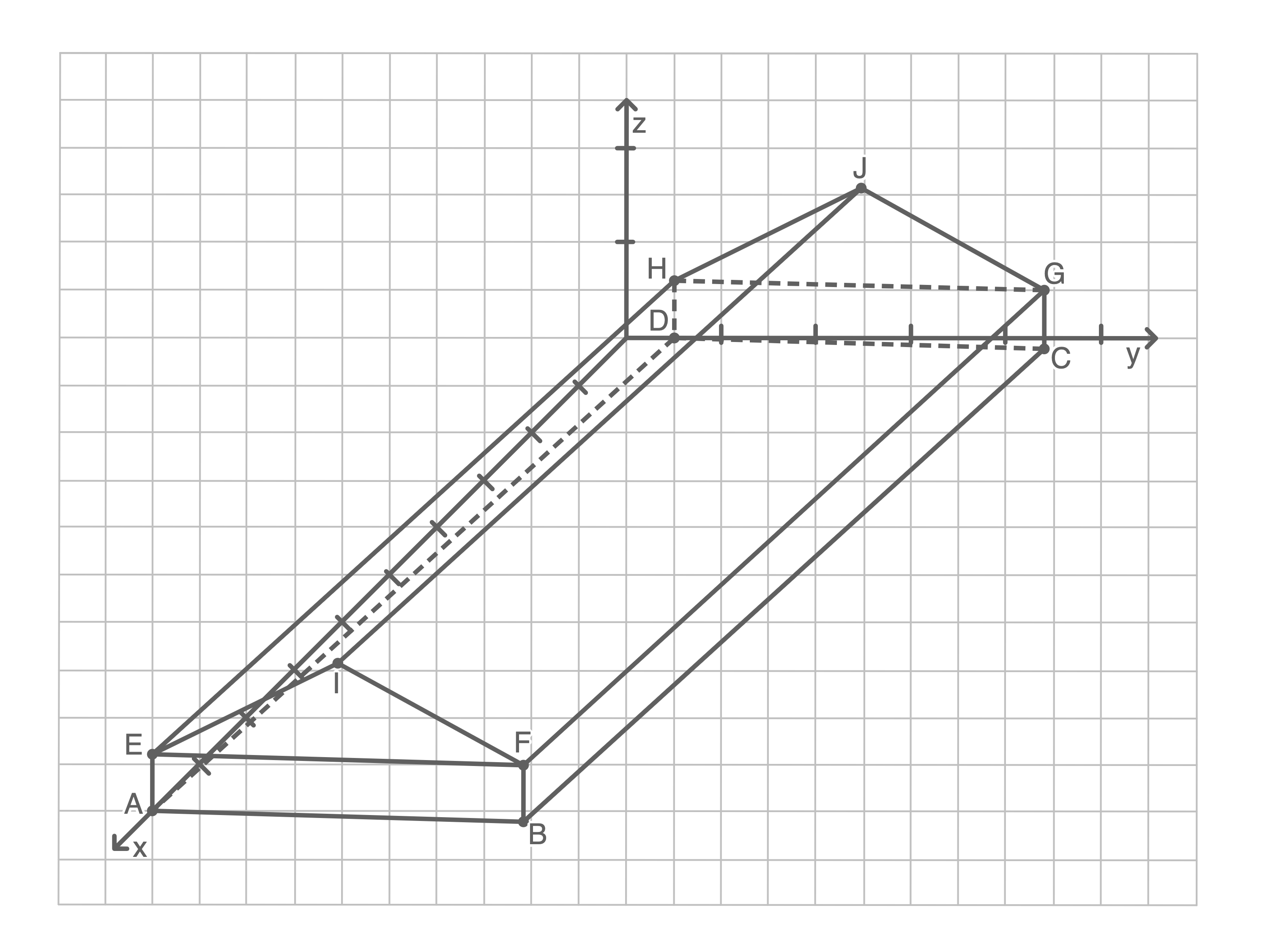

1.1
Gib die Koordinaten der Punkte  und
und  an.
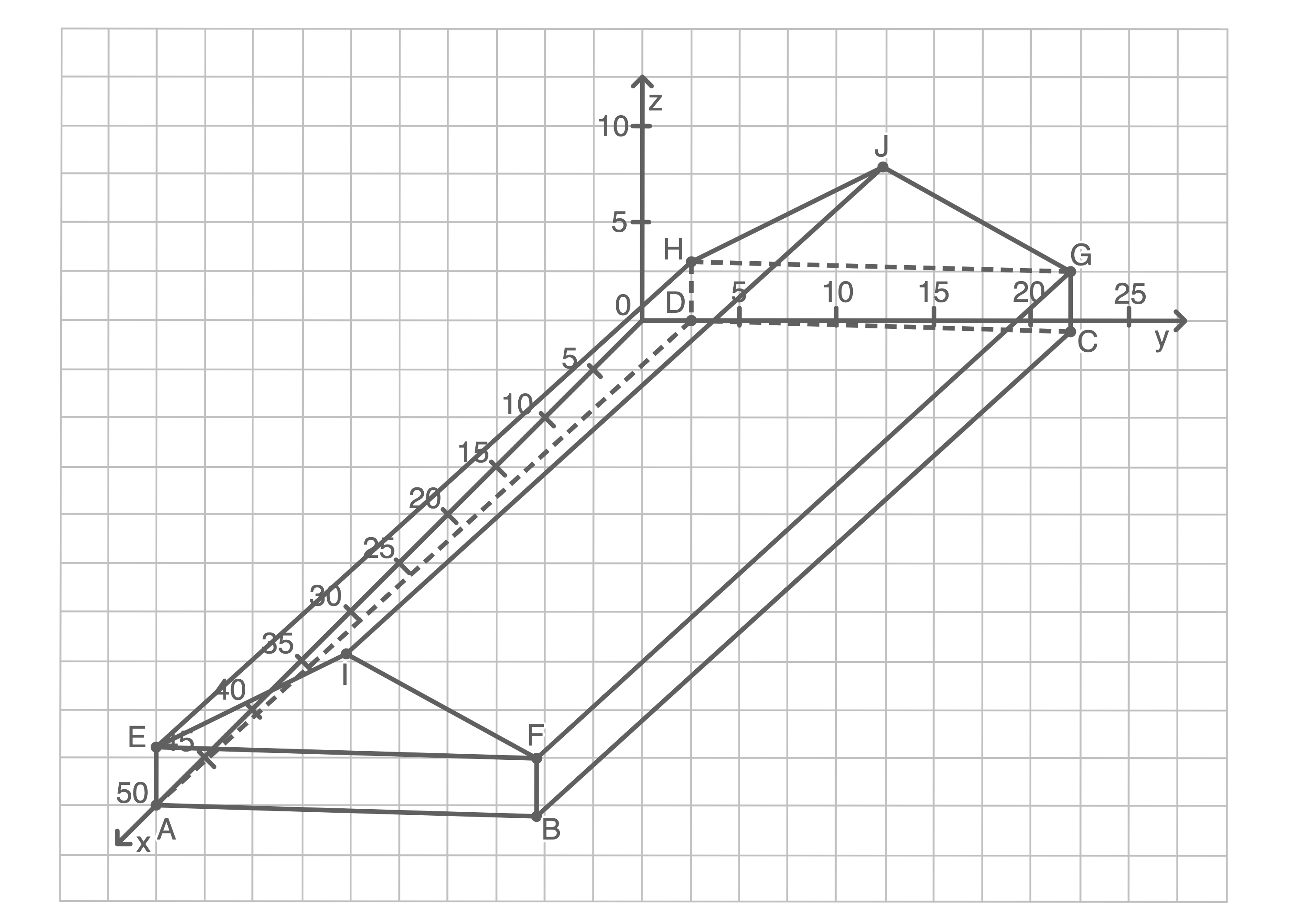
Beschrifte die Achsen im Material mit der fehlenden Skalierung.
an.
Beschrifte die Achsen im Material mit der fehlenden Skalierung.
(5 BE)
1.2
Berechne das Gesamtvolumen des Festzelts.
(4 BE)
1.3
Der Eingangsbereich  liegt in der Ebene
liegt in der Ebene  Gib eine Parametergleichung der Ebene
Gib eine Parametergleichung der Ebene  an und bestimme eine Koordinatengleichung dieser Ebene.
an und bestimme eine Koordinatengleichung dieser Ebene.
 Zur Kontrolle: Eine mögliche Koordinatengleichung ist
Zur Kontrolle: Eine mögliche Koordinatengleichung ist ![\(K: 20 x-y=1000. \big]\)](https://mathjax.schullv.de/edc9827c76de927dba22414ac24c3a4921b7f4f34747a8814254e0a6068402b6?color=5a5a5a)
(5 BE)
2
Gegeben ist die Ebenenschar 
2.1
Zeige, dass die Ebene  aus Aufgabe 1.3 eine Ebene der Schar
aus Aufgabe 1.3 eine Ebene der Schar  ist.
Begründe, dass alle Ebenen der Schar
ist.
Begründe, dass alle Ebenen der Schar  parallel zueinander verlaufen.
parallel zueinander verlaufen.
(3 BE)
2.2
Das Festzelt soll im Inneren einen separaten Bereich erhalten. Dafür wird eine zum Eingangsbereich  parallele Trennwand eingezogen. Im Modell liegt diese Trennwand in einer Ebene der Schar
parallele Trennwand eingezogen. Im Modell liegt diese Trennwand in einer Ebene der Schar  Erläutere hierzu die dargestellten Vorgehensweisen in den Zeilen
Erläutere hierzu die dargestellten Vorgehensweisen in den Zeilen  bis
bis  und gib die in der Zeile
und gib die in der Zeile  durch Auslassungspunkte gekennzeichneten fehlenden Berechnungen an.
Beschreibe abschließend die Lage der Trennwand.
durch Auslassungspunkte gekennzeichneten fehlenden Berechnungen an.
Beschreibe abschließend die Lage der Trennwand.
(7 BE)
3
Im Modell steht im Punkt  ein
ein  hoher, vertikal ausgerichteter Kirmesbaum. Die rechte Zeltwand, die durch die Punkte
hoher, vertikal ausgerichteter Kirmesbaum. Die rechte Zeltwand, die durch die Punkte  und
und  begrenzt wird, liegt in der Ebene
begrenzt wird, liegt in der Ebene 
3.1
Zu einem bestimmten Zeitpunkt des Festsamstags fällt das Sonnenlicht in Richtung des Vektors  ein.
Prüfe, ob der Schatten der Kirmesbaumspitze zu diesem Zeitpunkt auf die rechte Zeltwand trifft.
ein.
Prüfe, ob der Schatten der Kirmesbaumspitze zu diesem Zeitpunkt auf die rechte Zeltwand trifft.
(6 BE)
3.2
Im Modell ist im Punkt  der rechten Zeltwand ein punktförmiger Strahler angebracht, der genau in Richtung der Kirmesbaumspitze ausgerichtet ist. Der austretende Lichtstrahl verläuft unter einem Winkel von
der rechten Zeltwand ein punktförmiger Strahler angebracht, der genau in Richtung der Kirmesbaumspitze ausgerichtet ist. Der austretende Lichtstrahl verläuft unter einem Winkel von  zur Horizontalen.
Zeige, dass
zur Horizontalen.
Zeige, dass  gilt, und bestimme den Wert von
gilt, und bestimme den Wert von 
(5 BE)
4
Im Festzelt findet am Samstagabend eine Musikveranstaltung statt. Dazu werden vorab von drei Sponsoren  und
und  Freikarten für Sitzplätze in den Kategorien „VIP"
Freikarten für Sitzplätze in den Kategorien „VIP"  und „Normal“
und „Normal“  verlost.
In der Kategorie
verlost.
In der Kategorie  werden Freikarten für insgesamt 40 Sitzplätze und in der Kategorie
werden Freikarten für insgesamt 40 Sitzplätze und in der Kategorie  Freikarten für insgesamt 100 Sitzplätze verlost. Alle Freikarten finden Abnehmer.
Die folgende Tabelle gibt für die drei Sponsoren die (prozentualen) Anteile der beiden Kategorien an den jeweils verlosten Freikarten an.
Freikarten für insgesamt 100 Sitzplätze verlost. Alle Freikarten finden Abnehmer.
Die folgende Tabelle gibt für die drei Sponsoren die (prozentualen) Anteile der beiden Kategorien an den jeweils verlosten Freikarten an.
4.1
Deute den Wert  in der Tabelle im Sachzusammenhang.
Leite unter Angabe der Bedeutung der verwendeten Variablen ein lineares Gleichungssystem zur Berechnung der Anzahl der von den drei Sponsoren jeweils verlosten Freikarten her.
Berechne (ohne Betrachtung des Sachzusammenhangs) die Lösungsmenge des Gleichungssystems.
in der Tabelle im Sachzusammenhang.
Leite unter Angabe der Bedeutung der verwendeten Variablen ein lineares Gleichungssystem zur Berechnung der Anzahl der von den drei Sponsoren jeweils verlosten Freikarten her.
Berechne (ohne Betrachtung des Sachzusammenhangs) die Lösungsmenge des Gleichungssystems.
 zur Kontrolle: Ein mögliches Ergebnis ist
zur Kontrolle: Ein mögliches Ergebnis ist ![\(\mathbb{L} =\{(120-2 c \mid 20+c\mid c) \mid c \in \mathbb{R}\}.\bigg]\)](https://mathjax.schullv.de/6930d4c51d94316de4629fb79f788b2c4a19431b8bbb04ab033a34def96470f3?color=5a5a5a)
(6 BE)
4.2
Ermittle die zulässigen Werte des Parameters  in dem in Aufgabe 4.1 angegebenen Kontrollergebnis, wenn jeder der drei Sponsoren mindestens 20 der 140 Freikarten verlost.
in dem in Aufgabe 4.1 angegebenen Kontrollergebnis, wenn jeder der drei Sponsoren mindestens 20 der 140 Freikarten verlost.
(5 BE)
4.3
Ein Gleichungssystem, das weniger Gleichungen als Variablen besitzt, heißt unterbestimmt. Ein Gleichungssystem, das mehr Gleichungen als Variablen besitzt, heißt überbestimmt.
Beurteile (ohne Betrachtung des Sachzusammenhangs) die folgenden beiden Aussagen:
Aussage  „Jedes unterbestimmte Gleichungssystem besitzt eine Lösung.“
Aussage
„Jedes unterbestimmte Gleichungssystem besitzt eine Lösung.“
Aussage  „Es gibt überbestimmte Gleichungssysteme, die keine eindeutige Lösung besitzen.“
„Es gibt überbestimmte Gleichungssysteme, die keine eindeutige Lösung besitzen.“
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Koordinaten angeben



 Achsen beschriften
Achsen beschriften

1.2
1. Schritt: Volumen des quaderförmigen Unterbaus berechnen
 Damit folgt:
Damit folgt:
![\(\begin{array}[t]{rll}
V_U&=& | \overline{EH} |\cdot | \overline{AB} |\cdot | \overline{AE} | \\[5pt]
&=& 50,06\cdot 20,02\cdot 3 \\[5pt]
&=& 3006,6 \; [\,\text{m}^3] \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7fdaf109c76165e331cb165346b220add8ed2e6bac3062c684e02351ce99a810?color=5a5a5a) 2. Schritt: Volumen des Dachs berechnen
2. Schritt: Volumen des Dachs berechnen
![\(\begin{array}[t]{rll}
V_D&=& \dfrac{1}{2}\cdot |\overline{EF}|\cdot h\cdot |\overline{EH}| \\[5pt]
\end{array}\)](https://mathjax.schullv.de/46ffd837f1540fe4efe5ff30da86d34ef559ce65934c2099b0faf460299c43ba?color=5a5a5a) Die Höhe
Die Höhe  des Dachs ergibt sich aus Subtraktion der
des Dachs ergibt sich aus Subtraktion der  -Koordinaten der Punkte
-Koordinaten der Punkte  und
und  mit
mit ![\(h = z_J-z_E=8-3=5\; [\text{m}].\)](https://mathjax.schullv.de/1b6cb59c4cc188267429267779e4c919d20c1638499ca31a879e92411d9d62cc?color=5a5a5a) Außerdem gilt
Außerdem gilt ![\(|\overline{EF}| = |\overline{AB}| \approx 20,02\; [\text{m}].\)](https://mathjax.schullv.de/f3c237d9c5fc5c4b80c87c263c1b34bac0a2a16d33eb5053348773a721f6948f?color=5a5a5a)
![\(\begin{array}[t]{rll}
V_D &=& \dfrac{1}{2}\cdot 20,02\cdot 5\cdot 50,06 \\[5pt]
&\approx& 2505,5 \; [\text{m}^3] \\[5pt]
\end{array}\)](https://mathjax.schullv.de/acb809461a79064c1696876c60687d211e2dac5704011b5ea746191f073d6302?color=5a5a5a) 3. Schritt: Gesamtvolumen berechnen
3. Schritt: Gesamtvolumen berechnen
![\(\begin{array}[t]{rll}
V_{Ges}&=& V_U+V_D \\[5pt]
&=& 3006,6+2505,5 \\[5pt]
&=& 5512,1 \; [\text{m}^3]
\end{array}\)](https://mathjax.schullv.de/6171e36be6bdac15593933597d0529f9c230004e9583947eb578969ed9b29949?color=5a5a5a)
1.3
Parametergleichung angeben
Ebenengleichung ermitteln
Mittels Kreuzprodukt ergibt sich ein Normalenvektor von 
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=& \pmatrix{1\\20\\0} \times \pmatrix{0\\0\\3}&\\[5pt]
&=& \pmatrix{20\cdot 3-0\cdot 0\\0\cdot 0-3\cdot 1\\1\cdot 0-0\cdot 20}&\\[5pt]
&=& \pmatrix{60\\-3\\0} &\\[5pt]
&=& 3\cdot \pmatrix{20\\-1\\0}
\end{array}\)](https://mathjax.schullv.de/957960512c40efca84587066e4d7a62d0df4c194414b099307230fc82a219aa5?color=5a5a5a) Mit
Mit  folgt also:
Eine mögliche Koordinatengleichung ist somit
folgt also:
Eine mögliche Koordinatengleichung ist somit 
2.1
Es gilt:
![\(\begin{array}[t]{rll}
K: 20x-y&=& 1000 & \\[5pt]
20x-y&=& 2\cdot 500
\end{array}\)](https://mathjax.schullv.de/21a1277deef58041a0f0e0dd4e0f408c1189da874baa2f4192122f1aaca02a63?color=5a5a5a) Somit folgt
Somit folgt  Da die linke Seite der Koordinatengleichung unabhängig von
Da die linke Seite der Koordinatengleichung unabhängig von  bei allen Ebenen der Schar gleich ist und somit alle Ebenen der Schar die gleichen Normalenvektoren besitzen, verlaufen diese parallel zueinander.
bei allen Ebenen der Schar gleich ist und somit alle Ebenen der Schar die gleichen Normalenvektoren besitzen, verlaufen diese parallel zueinander.
2.2
Vorgehensweisen erklären
 Die Gerade
Die Gerade  verläuft orthogonal zum Eingangsbereich bzw. zur Ebene
verläuft orthogonal zum Eingangsbereich bzw. zur Ebene  durch den Punkt
durch den Punkt  Einer der Eckpunkte der Trennwand wird mit
Einer der Eckpunkte der Trennwand wird mit  bezeichnet und liegt auf
bezeichnet und liegt auf 
 Der Abstand zwischen
Der Abstand zwischen  und
und  soll
soll  betragen. Die Trennwand soll also 20 Meter hinter dem Eingangsbereich eingezogen werden.
betragen. Die Trennwand soll also 20 Meter hinter dem Eingangsbereich eingezogen werden.
 Für die Werte
Für die Werte  und
und  besitzen die Punkte der Gerade
besitzen die Punkte der Gerade  einen Abstand von 20 Metern zum Punkt
einen Abstand von 20 Metern zum Punkt  im Eingangsbereich. Mit
im Eingangsbereich. Mit  ergeben sich die Koordinaten des Punkts
ergeben sich die Koordinaten des Punkts  der innerhalb des Zelts liegt.
der innerhalb des Zelts liegt.
 Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in die Ebenenschar
in die Ebenenschar  liefert die Ebenengleichung
liefert die Ebenengleichung  Fehlende Berechnung angeben
Lage der Trennwand beschreiben
Die Trennwand liegt parallel zum Eingangsbereich
Fehlende Berechnung angeben
Lage der Trennwand beschreiben
Die Trennwand liegt parallel zum Eingangsbereich  lediglich um 20 Meter entlang der Strecke
lediglich um 20 Meter entlang der Strecke  in negative
in negative  -Richtung und somit in den hinteren Teil des Zeltes verschoben.
-Richtung und somit in den hinteren Teil des Zeltes verschoben.
3.1
1. Schritt: Geradengleichung aufstellen
Die Sonnenstrahlen, die auf die Kirmesbaumspitze  treffen, können mit folgender Gleichung beschrieben werden:
treffen, können mit folgender Gleichung beschrieben werden:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OS}+t\cdot \overrightarrow{v} \\[5pt]
&=& \pmatrix{26\\29,25\\14} +t\cdot \pmatrix{0\\-2\\-3}
\end{array}\)](https://mathjax.schullv.de/92ca5469cad69c5e16c5606cf856ffac26e12f3e87d18bb31a16ec2007f8b81c?color=5a5a5a) 2. Schritt: Schnittpunkt mit der Zeltwandebene bestimmen
Einsetzen der Geradengleichung in die Ebenengleichung
2. Schritt: Schnittpunkt mit der Zeltwandebene bestimmen
Einsetzen der Geradengleichung in die Ebenengleichung  der rechten Zeltwand:
Daraus ergibt sich der Schnittpunkt
der rechten Zeltwand:
Daraus ergibt sich der Schnittpunkt  der Sonnengerade mit der Zeltwandebene:
der Sonnengerade mit der Zeltwandebene:
 Da die Koordinaten des Schnittpunkts innerhalb des Rechtecks
Da die Koordinaten des Schnittpunkts innerhalb des Rechtecks  liegen, trifft der Schatten der Kirmesbaumspitze auf die rechte Zeltwand.
liegen, trifft der Schatten der Kirmesbaumspitze auf die rechte Zeltwand.
3.2
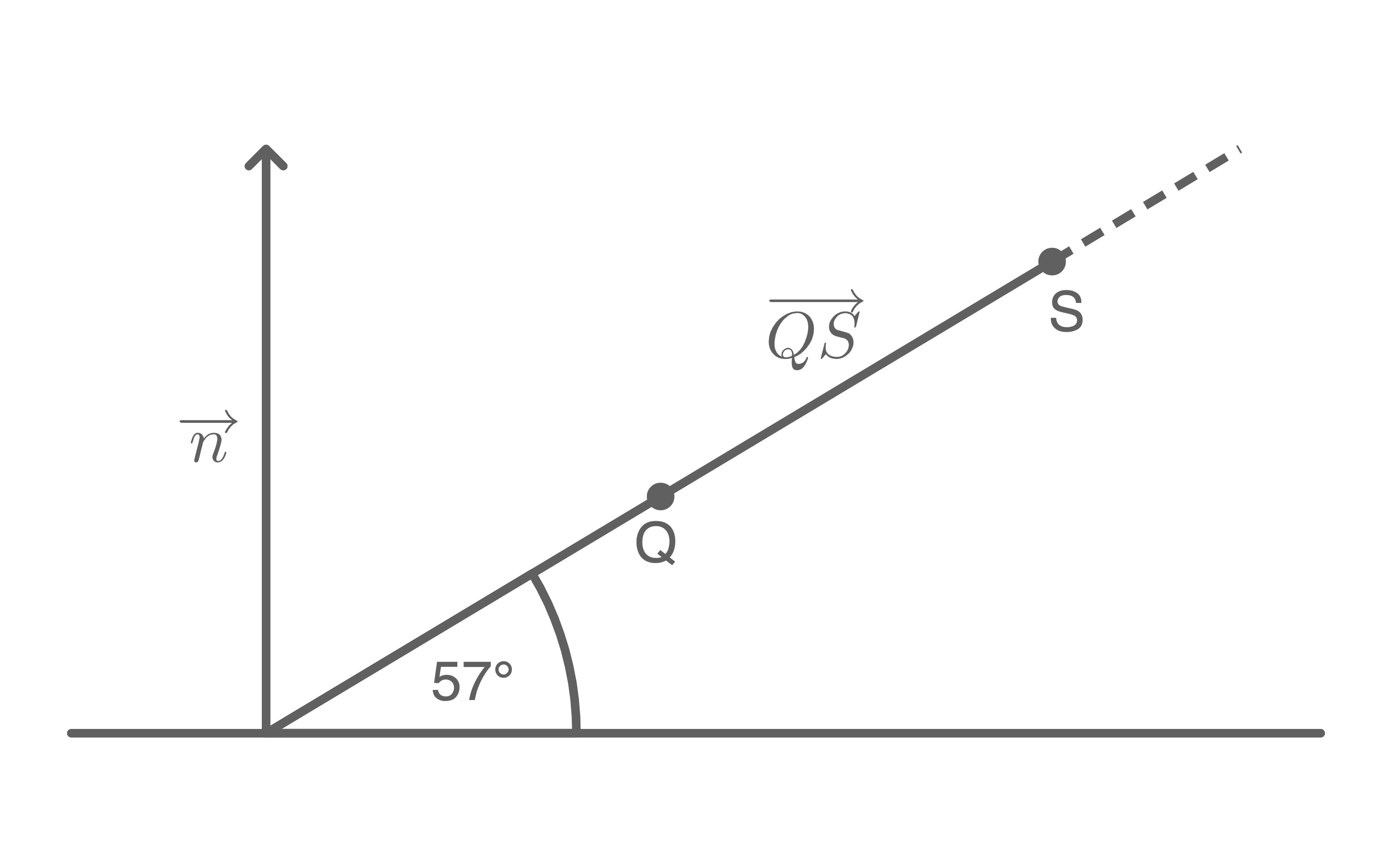
Hilfsskizze (nicht maßstäblich)
4.1
Wert deuten
Der Wert  beschreibt den Anteil der VIP-Tickets an der Gesamtanzahl der Tickets, die der Sponsor
beschreibt den Anteil der VIP-Tickets an der Gesamtanzahl der Tickets, die der Sponsor  verlost.
Lineares Gleichungssystem herleiten
verlost.
Lineares Gleichungssystem herleiten
 Gesamtanzahl der Freikarten, die von Sponsor A verlost werden
Gesamtanzahl der Freikarten, die von Sponsor A verlost werden
 Gesamtanzahl der Freikarten, die von Sponsor B verlost werden
Gesamtanzahl der Freikarten, die von Sponsor B verlost werden
 Gesamtanzahl der Freikarten, die von Sponsor C verlost werden
Aus der Tabelle ergibt sich nun folgendes Gleichunssystem:
Lösungsmenge berechnen
Aus
Gesamtanzahl der Freikarten, die von Sponsor C verlost werden
Aus der Tabelle ergibt sich nun folgendes Gleichunssystem:
Lösungsmenge berechnen
Aus  folgt:
folgt:
![\(\begin{array}[t]{rll}
b-c&=& 20&\quad \scriptsize \mid\; +c \\[5pt]
b&=& 20+c
\end{array}\)](https://mathjax.schullv.de/1fafe2350f398c19cb38174dc11967f0725b5638cffeff3ef246638fa19eb867?color=5a5a5a) Einsetzen in
Einsetzen in  ergibt:
Somit ist die Lösungsmenge des Gleichungssystems gegeben durch
ergibt:
Somit ist die Lösungsmenge des Gleichungssystems gegeben durch 
4.2
Damit Sponsor  eine passende Anzahl an Karten verlost, muss gelten:
eine passende Anzahl an Karten verlost, muss gelten:
 Für Sponsor
Für Sponsor  muss gelten:
muss gelten:
![\(\begin{array}[t]{rlcll}
20 &\leq & 120-2c &\leq & 140 &\quad \scriptsize \mid\;-120 \\[5pt]
-100 &\leq & -2c &\leq & 20 &\quad \scriptsize \mid\;:(-2) \\[5pt]
50&\geq & c &\geq& -10
\end{array}\)](https://mathjax.schullv.de/2226ead46c64af52e6a14dc9b5b848626e02920df130241a275d2cd05f315d34?color=5a5a5a) Für Sponsor
Für Sponsor  muss gelten:
muss gelten:
![\(\begin{array}[t]{rlcll}
20 &\leq & 20+c &\leq & 140 &\quad \scriptsize \mid\;-20 \\[5pt]
0 &\leq & c &\leq & 120
\end{array}\)](https://mathjax.schullv.de/958ab18e9e47045a966c0dcf7559621f3b460cc0603bab32ba8ae81bcbe61a98?color=5a5a5a) Aus allen drei Einschränkungen ergibt sich also
Aus allen drei Einschränkungen ergibt sich also 
4.3
Aussage  Die Aussage ist nicht korrekt. Beispielsweise ist folgendes Gleichungssystem unterbestimmt und besitzt keine Lösung:
Die Aussage ist nicht korrekt. Beispielsweise ist folgendes Gleichungssystem unterbestimmt und besitzt keine Lösung:
 Aussage
Aussage  Die Aussage ist korrekt.
Beispielsweise ist folgendes Gleichungssystem überbestimmt, besitzt aber keine eindeutige Lösung:
Die Aussage ist korrekt.
Beispielsweise ist folgendes Gleichungssystem überbestimmt, besitzt aber keine eindeutige Lösung:
 Alle drei Gleichungen sind linear abhängig, wodurch das Gleichungssystem keine eindeutige Lösung besitzt.
Alle drei Gleichungen sind linear abhängig, wodurch das Gleichungssystem keine eindeutige Lösung besitzt.