C2.1 - Stochastik

Bei der Aussaat von Raps können Landwirte aus verschiedenen Sorten mit jeweils spezifischen Eigenschaften wählen.
Zunächst wird der Fall betrachtet, dass ein Landwirt Saatgut einer Sorte $A$ ausgebracht hat, die unter den vorliegenen Bedingungen mit einer Wahrscheinlichkeit von $95 \,\%$ keimt.

1.1

Es werden dem Boden zufällig einige Körner entnommen und untersucht, ob diese gekeimt haben. Erläutere die untenstehende Gleichung sowie die einzelnen Faktoren des Terms auf der rechten Seite der Gleichung in diesem Sachzusammenhang. Gib den zugehörigen Zahlenwert an.
$P(X=55)=\pmatrix{60\\55}\cdot 0,95^{55}\cdot 0,05^5$
Begründe, warum das zugrunde gelegte mathematische Modell hier angewendet werden kann.

(5 BE)

1.2

Bestimme die Wahrscheinlichkeit folgender Ereignisse:
$E_1$ : Unter $80$ dem Boden zufällig entnommenen Körnern haben höchstens $4$ nicht gekeimt.
$E_2$ : Unter $80$ dem Boden zufällig entnommenen Körnern weicht die Anzahl der gekeimten Körner höchstens um $2$ vom zu erwartenden Wert ab.

(5 BE)

1.3

Der Landwirt vermutet, dass der Anteil der Samenkörner der Sorte $A,$ die unter den vorliegenden Bedingungen keimen, niedriger ist als $95 \,\%$ .

1.3.1

Entwickle einen Hypothesentest auf einem Signifikanzniveau von $5 \,\%$ , mit dem bei $250$ zufällig dem Boden entnommenen Körnern die Vermutung überprüft werden könnte. Formuliere im Sachzusammenhang eine Entscheidungsregel.
Beschreibe den Fehler 2. Art im Sachzusammenhang.

(8 BE)

1.3.2

Bestimme mithilfe deiner Entscheidungsregel aus Aufgabe 1.3.1 die Wahrscheinlichkeit für einen Fehler 2. Art für den Fall, dass der Anteil der Körner, die gekeimt haben, tatsächlich nur $90 \,\%$ beträgt.
Beschreibe, wie die Fehlerwahrscheinlichkeit für einen Fehler 2. Art reduziert werden könnte, obwohl das Signifikanzniveau weiterhin eingehalten werden soll.

(4 BE)

Betrachtet wird nun der Fall, dass der Landwirt sich für unterschiedliche Sorten entscheidet. Er sät auf $85 \,\%$ seiner für Raps vorgesehenen Fläche Samenkörner der Sorte $A$ aus Aufgabe 1. Auf der restlichen für Raps vorhergesehenen Fläche sät er Samenkörner der Sorte $B,$ die unter den vorliegenden Bedingungen mit einer Wahrscheinlichkeit von $90 \,\%$ keimen.
Die verwendeten Mengen an Saatgut sind hierbei proportional zur Größe der genutzten Flächen.

2.1

Berechne die Wahrscheinlichkeit, dass ein nach der Aussaat dem Boden zufällig entnommenes Korn, welches gekeimt hat, ein Korn der Sorte $B$ ist.

(4 BE)

2.2

Zeige, dass die Wahrscheinlichkeit, dass ein nach der Aussaat dem Boden zufällig entnommenes Korn nicht gekeimt hat, $5,75 \,\%$ beträgt.

(2 BE)

2.3

Eine junge Pflanze, die aus einem Samenkorn durch Keimung entsteht, wird als Sämling bezeichnet. In manchen Jahren werden diese von Schnecken angefressen. Der Landwirt stellt fest, dass insgesamt $20 \,\%$ aller Rapssämlinge angefressen wurden und insbesondere, dass $30 \,\%$ der Rapssämlinge der Sorte $B$ angefressen wurden.
Erläutere im Sachzusammenhang, was im Folgenden berechnet wird:

$\dfrac{0,15\cdot 0,9\cdot 0,3}{0,9425\cdot 0,2}$

(4 BE)

Bei der Aussaat von Raps gibt es die Varianten Drillsaat und Einzelkornsaat. Bei letzterer erhofft man sich neben einer Reduzierung der benötigten Menge an Saatgut durch eine gleichmäßige Verteilung des Saatguts auf das Feld besonders gute Erträge. Die Körner werden einzeln durch eine Maschine in Reihen auf dem Feld abgelegt. Im Untersuchungsbericht eines Modellversuchs wird festgestellt, dass die Zufallsgröße $Y$ : „Abstand zwischen zwei benachbarten Körnern innerhalb einer Reihe“ normalverteilt ist. Ferner habe man ermittelt, dass der Mittelwert $5\,\text{cm}$ und die Standardabweichung $1,5\,\text{cm}$ beträgt.
Bestimme jeweils, mit welcher Wahrscheinlichkeit für einen zufällig ausgewählten und gemessenen Abstand zweier benachbarter Körner gemäß dieses Untersuchungsberichts Folgendes gilt:
$A:$ Der Abstand weicht um maximal $1\,\text{cm}$ vom Mittelwert ab.
$B:$ Der Abstand weicht um mindestens $2\,\text{cm}$ vom Mittelwert ab.

(5 BE)

Abstand (in cm) im Intervall	Absolute Häufigkeit
$\color{#fff}{[0;1)}$	$60$
$\color{#fff}{[1;2)}$	$43$
$\color{#fff}{[2;3)}$	$30$
$\color{#fff}{[3;4)}$	$21$
$\color{#fff}{[4;5)}$	$15$
$\color{#fff}{[5;6)}$	$11$
$\color{#fff}{[6;7)}$	$8$
$\color{#fff}{[7;8)}$	$5$
$\color{#fff}{[8;9)}$	$4$
$\color{#fff}{[9;10)}$	$3$
$\color{#fff}{[10;\infty)}$	$0$

Material 1: Häufigkeitsverteilung von Kornabständen bei Drillsaat $(n=200)$

Bei einer genaueren Untersuchung der Resultate einer Drillsaatmaschine, welche die Körner ungenauer und im Mittel näher beieinander ablegt, hat man die im Material dargestellten Beobachtungen zu den Abständen benachbarter Körner gemacht. Es wird die Zufallsvariable $Z:$ „Abstand zwischen zwei benachbarten Körnern innerhalb einer Reihe“ betrachtet.

4.1

Stelle die Daten aus dem Material unter Verwendung der zugehörigen relativen Häufigkeiten in Form eines Säulendiagramms dar.

(4 BE)

4.2

Erläutere anhand der Daten, warum zur Beschreibung der Verteilung des Kornabstands $Z$ eine Exponentialfunktion $f$ der Form $f(z)=a\cdot \mathrm e^{-b\cdot z},a,b\gt 0,$ für $z\geq 0$ als Dichtefunktion geeignet ist.

(2 BE)

4.3

Es gilt $P(0\leq Z\leq u)$ $=\displaystyle\int_{0}^{u}f(z)\;\mathrm dz$ $=\dfrac{a}{b}\cdot \left(1-\mathrm e^{-b\cdot u}\right)$ und somit $\lim\limits_{u\to\infty}\left(P\left(0\leq Z\leq u \right)\right)=\dfrac{a}{b}.$
Begründe, dass hieraus $a=b$ folgt und bestätige mithilfe der relativen Häufigkeit für das Intervall $[0;1),$ dass $a=b\approx 0,36$ gilt.

(4 BE)

4.4

Die Verteilung des Kornabstands $Z$ wird nun für $z\geq0$ durch die Dichtefunktion $f$ mit $f(z)=0,365\cdot \mathrm e^{-0,365\cdot z}$ modelliert. Es gilt beispielsweise $P(0\leq Z\leq 3)=\displaystyle\int_{0}^{3}f(z)\;\mathrm dz \approx 66,55 \;\%.$ Erläutere die Bedeutung dieses Ergebnisses im Sachzusammenhang und prüfe, ob dieser Wert in guter Näherung mit der Häufigkeitsverteilung im Material übereinstimmt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Gleichung erläutern

Mit der Gleichung wird die Wahrscheinlichkeit berechnet, dass von $60$ Körnern genau $55$ keimen.

$\pmatrix{60\\55}:$ Anzahl Möglichkeiten, dass von $60$ Körnern genau $55$ keimen

$0,95^{55}:$ Wahrscheinlichkeit, dass $55$ Körner mit einer Wahrscheinlichkeit von jeweils $95\,\%$ keimen

$0,05^5:$ Wahrscheinlichkeit, dass $5$ Körner mit einer Wahrscheinlichkeit von jeweils $5\,\%$ nicht keimen

Wert der Gleichung angeben

$P(X=55) \approx 0,1016 = 10,16 \%$

Modell begründen

Das Modell der Binomialverteilung kann in diesem Fall verwendet werden, da es genau zwei mögliche Ereignisse gibt (keimen oder nicht keimen) und sich die Wahrscheinlichkeit für das Eintreffen dieser Ereignisse nicht verändert.

1.2

Die Zufallsgröße $X$ beschreibt die Anzahl der aufkeimenden Körner. $X$ ist $B_{80; 0,95}$ -verteilt.

$\begin{array}[t]{rll} E_1: \; P(X \geq 76) &=& 1 - P(X \leq 75) & \\[5pt] & \approx& 0,6289 \end{array}$

Der Erwartungswert $E(X)$ beträgt $n\cdot p= 80 \cdot 0,95 = 76.$

Rechenweg anzeigen

$E_2: \; P(74 \leq X \leq 78)=0,8086$

1.3.1

Hypothesentest

Es soll ein linksseitiger Hypothesentest durchgeführt werden:

$H_0: p \geq 0,95 \qquad H_1: p \lt 0,95 \qquad$ $\alpha = 0,05$

Sei $X$ die Anzahl der aufkeimenden Körner. $X$ ist $B_{250; 0,95}$ -verteilt.

Der Ablehnungsbereich wird durch $A = \{0; 1; \dots ; g \}$ definiert.

Gesucht ist die größte natürliche Zahl $g$ , sodass Folgendes gilt:

$\begin{array}[t]{rll} P(X \leq g)& \leq& 0,05&\quad \scriptsize \\[5pt] \end{array}$

Durch systematisches Ausprobieren mit dem Taschenrechner folgt:

$P (X \leq 232) = 0,0788$
$P(X \leq 231) = 0,0474$

Damit gilt für den Ablehnungsbereich: $A = \{0; \dots ; 231 \}$ .

Entscheidungsregel

Wenn maximal $231$ Körner aufkeimen, wird die Nullhypothese abgelehnt. Wenn mindestens $232$ Körner aufkeimen, wird die Nullhypothese nicht abgelehnt.

Fehler $2.$ Art im Sachzusammenhang beschreiben

Der Fehler $2$ . Art bedeutet, dass die Nullhypothese fälschlicherweise nicht abgelehnt wird, obwohl die Alternativhypothese korrekt ist.

Im Sachzusammenhang bedeutet der Fehler 2. Art folglich:

Es wird fälschlicherweise angenommen, dass die Körner mit einer Wahrscheinlichkeit von mehr als $95\,\%$ aufkeimen, da dies nach der Entscheidungsregel von dem Versuchsergebnis gilt. In Wirklichkeit keimen jedoch weniger als $95\,\%$ auf.

1.3.2

Wahrscheinlichkeit für einen Fehler 2. Art

Aus der Entscheidungsregel ergibt sich folgender Annahmebereich für $H_0: A =\{232; \dots; 250 \}$ . Zu ermitteln ist die Wahrscheinlichkeit, dass die Anzahl $X$ der aufgekeimten Körner im Annahmebereich $A$ liegt, obwohl die Wahrscheinlichkeit dafür, dass die Körner aufkeimen, nur $90 \%$ beträgt. Dabei gilt $n = 250$ und $p = 0,9$ .

$\begin{array}[t]{rll} P(X \geq 232)&=&1 - P(X \leq 231) & \\[5pt] &\approx& 0,0808 \end{array}$

Fehlerwahrscheinlichkeit reduzieren

Die Wahrscheinlichkeit für den Fehler $2$ . Art lässt sich reduzieren, indem die Anzahl der überprüften Körner erhöht wird.

2.1

$K$ : Das Korn ist aufgekeimt

$B$ : Das Korn ist von der Sorte B

Die Wahrscheinlichkeit, dass es sich um ein aufgekeimtes Korn handelt, ist gegeben durch $P(K)=0,85 \cdot 0,95 + 0,15 \cdot 0,9.$ Die Wahrscheinlichkeit, dass es sich dabei um ein Korn der Sorte B handelt, wird wie folgt berechnet:

Rechenweg anzeigen

$P_K(B)=14,32 \,\%$

2.2

Für jede Sorte von Samenkorn wird die Wahrscheinlichkeit berechnet, dass ein Korn nicht aufkeimt:

$P(A\cap\overline{K})=0,85 \cdot (1-0,95)=0,0425$

$P(B\cap\overline{K})=0,15 \cdot (1-0,9)=0,015$

Die Wahrscheinlichkeit, dass ein zufällig entnommenes Korn nicht keimt ist somit gegeben durch $0,0425+0,0075=0,0575=5,75\,\%.$

2.3

1. Schritt: Zähler interpretieren

Im Zähler wird mit $0,15\cdot 0,9 \cdot 0,3$ die Wahrscheinlichkeit beschrieben, dass ein zufällig dem Boden entnommenes Korn von der Sorte $B$ ist, welches aufgekeimt ist und durch Schnecken angefressen wurde.

2. Schritt: Nenner interpretieren

Es gilt $0,9425 = (1-0,0575).$ Dies entspricht der Gegenwahrscheinlichkeit zum Ergebnis aus Aufgabe 2.2, also der Gegenwahrscheinlichkeit dazu, dass ein dem Boden zufällig entnommenes Korn gekeimt hat.

Damit wird im Nenner mit $0,9425\cdot 0,2$ die Wahrscheinlichkeit beschrieben, dass ein zufällig dem Boden entnommenes Korn aufgekeimt ist und durch Schnecken angefressen wurde.

3. Schritt: Gesamtinterpretation

Insgesamt wird berechnet, mit welcher Wahrscheinlichkeit ein dem Boden zufällig entnommener aufgekeimter und angefressener Sämling von der Sorte $B$ ist.

Aus der Aufgabenstellung gehen $\mu = 5 \,\text{cm}$ und $\sigma = 1,5 \,\text{cm}$ hervor.

Da die Normalverteilung symmetrisch um den Mittelwert $\mu = 5 \,\text{cm}$ ist, gilt:

Ereignis A

$\begin{array}[t]{rll} P(A)&=&P(4 \leq X \leq 6) & \\[5pt] &=&P(X\leq6)-P(X\leq 3)& \\[5pt] &\approx& 0,5 \end{array}$

Ereignis B

$\begin{array}[t]{rll} P(B)&=&P(X \geq 7) + P(X \leq 3) & \\[5pt] &=& 2 \cdot P(X \leq 3) & \\[5pt] &\approx& 0,18 \end{array}$

Die Wahrscheinlichkeit für Ereignis $A$ beträgt somit $50 \%$ und für Ereignis $B$ $18 \%.$

4.1

Um die relative Häufigkeit zu berechnen, muss die absolute Häufigkeit durch die Anzahl $n$ aller Häufigkeiten geteilt werden. Es gilt $n=200.$

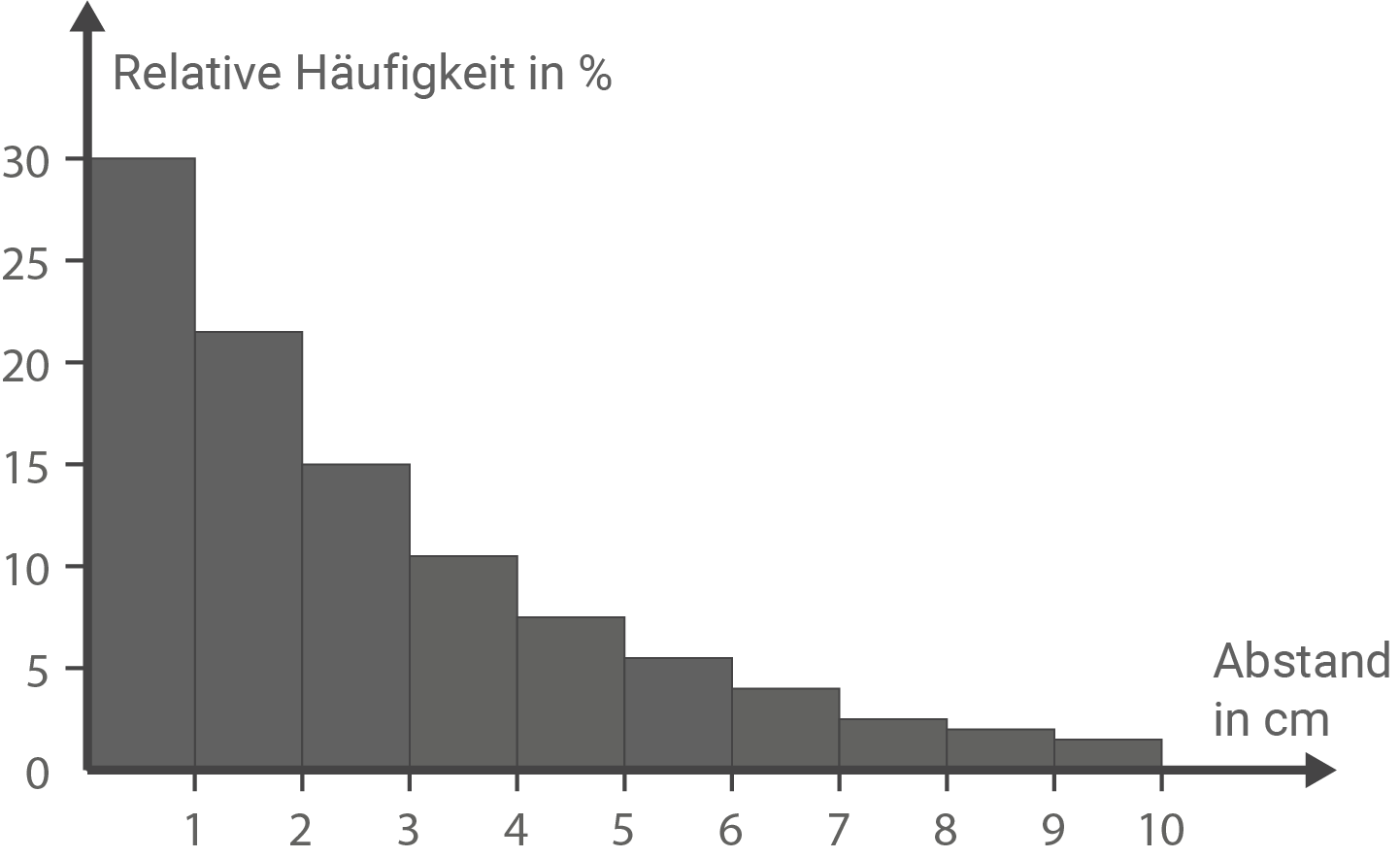
Abstand (in cm) im Intervall	Relative Häufigkeit in %
$[0;1)$	$30$
$[1;2)$	$21,5$
$[2;3)$	$15$
$[3;4)$	$10,5$
$[4;5)$	$7,5$
$[5;6)$	$5,5$
$[6;7)$	$4$
$[7;8)$	$2,5$
$[8;9)$	$2$
$[9;10)$	$1,5$
$[10;\infty)$	$0$

Säulendiagramm der Häufigkeitsverteilung

Balkendiagramm Relative Haeufigkeit Hessen Abi

4.2

Anhand des Säulendiagramms lässt sich erkennen, dass die Beschreibung des Kornabstands $Z$ einem Ausschnitt einer an der $y$ -Achse gespiegelten Exponentialfunktion entspricht.

Mit Zunahme der Abstände nimmt die relative Häufigkeit monoton ab und nimmt ab einem Abstand von $10\,\text{cm}$ den Wert null an.

Eine allgemeine Funktion dafür wird gerade durch $f(z) = a \cdot \mathrm{e}^{-b \cdot z}$ mit $a,b \gt 0$ beschrieben.

4.3

Folgerung begründen

Da es sich um eine Dichtefunktion handelt, muss die gesamte Fläche unterhalb dieser Funktion der Gesamtwahrscheinlichkeit $100\,\%,$ also $1$ entsprechen. Damit muss Folgendes gelten:

$\begin{array}[t]{rll} \lim\limits_{u\to\infty}P(0 \leq Z \leq u)&=& 1&\quad \scriptsize \\[5pt] \dfrac{a}{b} &=& 1 & \quad \scriptsize \mid\; \cdot b \\[5pt] a& =& b& \end{array}$

Aussage bestätigen

Für das Integral im Intervall $[0;1)$ gilt mit $a=b:$

Vollständigen Rechenweg anzeigen

$b \approx 0,36$

Damit gilt $a = b \approx 0,36$ .

4.4

Im Sachzusammenhang beschreibt das Ergebnis die Wahrscheinlichkeit dafür, dass ein zufällig gemessener Abstand zweier Körner maximal $3 \,\text{cm}$ beträgt.

Durch Berechnen dieser Wahrscheinlichkeit anhand der Häufigkeitsverteilung im Material folgt:

$\dfrac{60}{200} + \dfrac{43}{200} + \dfrac{30}{200} = 0,665$ $= 66,5 \%$

Damit ist der durch die Funktion $f$ berechnete Wert eine gute Näherung an den exakten Wert aus dem Material.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?