A2 - Analysis
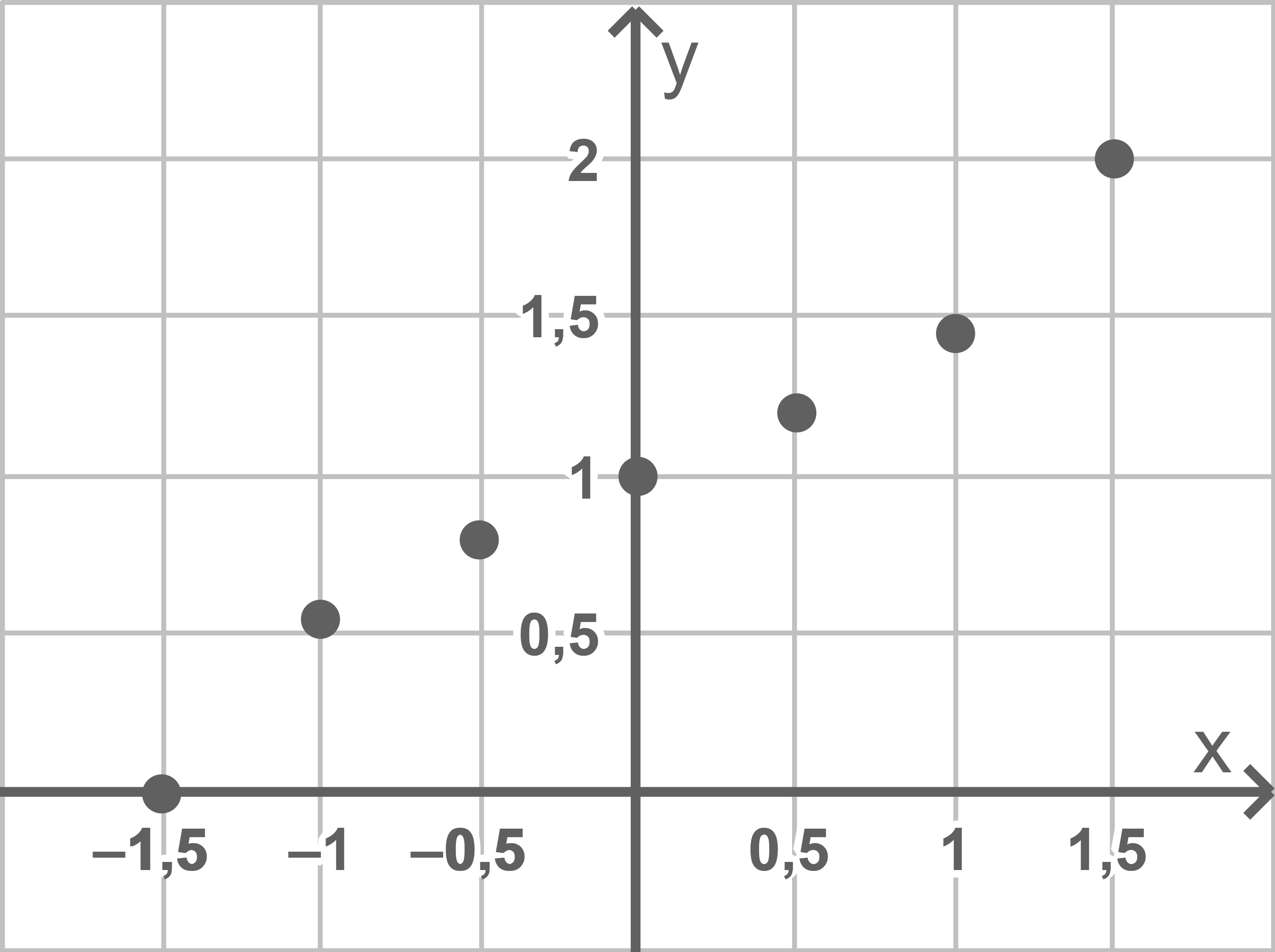
Eine Schokoladenglocke soll mathematisch modelliert werden. Dazu werden an sieben verschiedenen Stellen die Radien der Glocke gemessen. Im Material 1 sind die Messdaten als Punkte eingetragen. Die Punkte liegen auf dem oberen Rand der Querschnittsfläche, die bei einem Querschnitt durch eine Symmetrieebene der Glocke entsteht. Durch Rotation des oberen Randes der Querschnittsfläche um die  -Achse erhält man die Glockenform.
-Achse erhält man die Glockenform.
Die Wertetabelle gibt die im Koordinatensystem eingetragenen Punkte an. Eine Einheit entspricht dabei einem Zentimeter.
 Material 2
Methode A:
Material 2
Methode A:
Lässt man den Graphen einer Funktion für
für  um die
um die  -Achse rotieren, dann lässt sich der Flächeninhalt
-Achse rotieren, dann lässt sich der Flächeninhalt  der Mantelfläche des Rotationskörpers folgendermaßen mit Hilfe eines Integrals ermitteln:
der Mantelfläche des Rotationskörpers folgendermaßen mit Hilfe eines Integrals ermitteln:


 Methode B:
Der Flächeninhalt
Methode B:
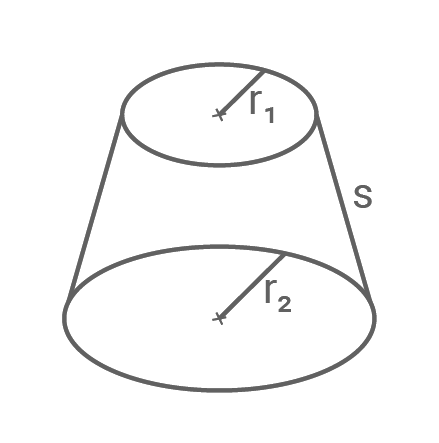
Der Flächeninhalt  der Mantelfläche eines geraden Kreiskegelstumpfs lässt sich mit folgender Formel berechnen:
der Mantelfläche eines geraden Kreiskegelstumpfs lässt sich mit folgender Formel berechnen:


Die Wertetabelle gibt die im Koordinatensystem eingetragenen Punkte an. Eine Einheit entspricht dabei einem Zentimeter.
1.
Die Form des oberen Randes der Querschnittsfläche soll in einem ersten Modell anhand der in der Wertetabelle gegebenen Punkte annähernd durch den Graphen einer ganzrationalen Funktion  beschrieben werden.
beschrieben werden.
1.1
Begründe unter Verwendung von Material 1, warum die ganzrationale Funktion  mindestens dritten Grades sein muss.
mindestens dritten Grades sein muss.
(4 BE)
1.2
Bestimme eine ganzrationale Funktion  dritten Grades so, dass ihr Graph durch
dritten Grades so, dass ihr Graph durch  und
und  verläuft und in
verläuft und in  einen Wendepunkt besitzt.
einen Wendepunkt besitzt.
(8 BE)
1.3
Begründe, dass es keine ganzrationale Funktion dritten Grades geben kann, die durch alle in der Wertetabelle gegebenen Punkte verläuft und in  einen Wendepunkt besitzt.
einen Wendepunkt besitzt.
(3 BE)
2.
Eine weitere Möglichkeit, eine Näherungsfunktion für die Datenpunkte zu erhalten ist die Methode der Regression.
2.1
Gib eine mit Hilfe dieser Methode bestimmte ganzrationale Funktion  dritten Grades an, welche die Datenpunkte der Tabelle annähert. Die Koeffizienten sollen auf vier Nachkommastellen gerundet sein.
dritten Grades an, welche die Datenpunkte der Tabelle annähert. Die Koeffizienten sollen auf vier Nachkommastellen gerundet sein.
(3 BE)
2.2
Bestimme als Näherungswert für das Volumen der Glocke das Volumen des Rotationskörpers, der durch Rotation des Graphen der Funktion  im Intervall
im Intervall ![\([-1,5;1,5]\)](https://mathjax.schullv.de/95a8eab160b321fbd0798c793caea028e422cc35c2182c7449b2ca241ede2b92?color=5a5a5a) um die
um die  -Achse entsteht.
-Achse entsteht.
Solltest du den Funktionsterm von in Aufgabe 2.1 nicht bestimmt haben, verwende die Ersatzfunktion
in Aufgabe 2.1 nicht bestimmt haben, verwende die Ersatzfunktion  mit
mit 
Solltest du den Funktionsterm von
(3 BE)
3.
Die Form des oberen Randes der Querschnittsfläche soll in einem dritten Modell in einer Umgebung von  für eine geeignete Wahl des Parameters
für eine geeignete Wahl des Parameters  näherungsweise durch einen Graphen der Funktionenschar
näherungsweise durch einen Graphen der Funktionenschar  mit
mit 

 und
und  beschrieben werden.
beschrieben werden.
Berechne die Funktionsgleichungen der ersten drei Ableitungen der Funktionenschar . Zeige, dass alle Graphen der Schar
. Zeige, dass alle Graphen der Schar  genau einen Wendepunkt besitzen, und entscheide, ob dort ein Wechsel von einer Rechts- in eine Linskrümmung oder ein Wechsel von einer Links- in eine Rechtskrümmung erfolgt.
genau einen Wendepunkt besitzen, und entscheide, ob dort ein Wechsel von einer Rechts- in eine Linskrümmung oder ein Wechsel von einer Links- in eine Rechtskrümmung erfolgt.
Berechne die Funktionsgleichungen der ersten drei Ableitungen der Funktionenschar
(7 BE)
4.
Die Schokoladenglocke soll mit Blattgold verziert werden. Dazu wird eine extrem dünne, essbare Blattgoldfolie benötigt. Das Blattgold soll in einem Streifen von  bis
bis  rund um die Glocke aufgetragen werden. Um einen ersten Näherungswert für den Materialbedarf zu erhalten, wird zunächst vereinfachend eine Funktion
rund um die Glocke aufgetragen werden. Um einen ersten Näherungswert für den Materialbedarf zu erhalten, wird zunächst vereinfachend eine Funktion  betrachtet, deren Graph vom Punkt
betrachtet, deren Graph vom Punkt  bis zum Punkt
bis zum Punkt  geradlinig verläuft und in diesem Intervall um die
geradlinig verläuft und in diesem Intervall um die  -Achse rotiert.
-Achse rotiert.
Es ergibt sich die Form eines geraden Kegelstumpfs. Als Maß für den Materialbedarf dient der Flächeninhalt der Mantelfläche des Kegelstumpfs.
Es ergibt sich die Form eines geraden Kegelstumpfs. Als Maß für den Materialbedarf dient der Flächeninhalt der Mantelfläche des Kegelstumpfs.
4.1
Zeige, dass beim Bestimmen des Flächeninhalts der Mantelfläche des Kegelstumpfs, der bei Rotation des Graphen von  für
für  um die
um die  -Achse entsteht, beide in Material 2 angegebenen Methoden A und B zum gleichen Ergebnis führen.
-Achse entsteht, beide in Material 2 angegebenen Methoden A und B zum gleichen Ergebnis führen.
(7 BE)
4.2
Bestimme mit Hilfe der Methode A den Inhalt der mit Blattgold bedeckten Fläche unter Verwendung der Scharkurve von  aus Aufgabe 3 für
aus Aufgabe 3 für  und vergleiche das Ergebnis mit dem Ergebnis aus Aufgabe 4.1.
und vergleiche das Ergebnis mit dem Ergebnis aus Aufgabe 4.1.
Material 1
(5 BE)

Lässt man den Graphen einer Funktion

1.1
Zwischen den Punkten  und
und  weist der Graph eine Rechtskrümmung auf. Vom Punkt
weist der Graph eine Rechtskrümmung auf. Vom Punkt  bis zum Punkt
bis zum Punkt  existiert allerdings eine Linkskrümmung. Es handelt sich bei
existiert allerdings eine Linkskrümmung. Es handelt sich bei  somit um einen Wendepunkt und die ganzrationale Funktion muss damit mindestens Grad drei haben.
somit um einen Wendepunkt und die ganzrationale Funktion muss damit mindestens Grad drei haben.
1.2
Eine ganzrationale Funktion  dritten Grades hat die allgemeine Form
dritten Grades hat die allgemeine Form  und soll die Punkte
und soll die Punkte  ,
,  und
und  durchlaufen, wobei
durchlaufen, wobei  ein Wendepunkt ist.
ein Wendepunkt ist.
Mit Hilfe des CAS folgt, dass die zweite Ableitung von durch
durch  gegeben ist. Mit dem notwendingen Kriterium für Wendestellen ergibt sich folgendes Gleichungssystem:
Mit Hilfe der folgenden Befehle wird das Gleichungssystem nun mit dem CAS gelöst:
gegeben ist. Mit dem notwendingen Kriterium für Wendestellen ergibt sich folgendes Gleichungssystem:
Mit Hilfe der folgenden Befehle wird das Gleichungssystem nun mit dem CAS gelöst:
 Für die Variablen folgt damit:
Für die Variablen folgt damit:




 Für die gesuchte Funktion
Für die gesuchte Funktion  folgt damit:
folgt damit:




Mit Hilfe des CAS folgt, dass die zweite Ableitung von
on  Calculator
Calculator  Menu
Menu  Algebra
Algebra  Gleichungssysteme lösen
Gleichungssysteme lösen  System linearer Gleichungen lösen...
System linearer Gleichungen lösen...  Anzahl der Gleichungen: 4
Anzahl der Gleichungen: 4  Variablen: Variablennamen mit Komma getrennt eingeben
Variablen: Variablennamen mit Komma getrennt eingeben  OK
OK


1.3
Einsetzen des Punktes  in die in der vorherigen Teilaufgabe bestimmten Funktion liefert:
in die in der vorherigen Teilaufgabe bestimmten Funktion liefert:





 Der Punkt aus der Wertetabelle liegt nicht auf
Der Punkt aus der Wertetabelle liegt nicht auf  somit kann keine ganzrationale Funktion dritten Grades existieren, welche die Forderungen erfüllt.
somit kann keine ganzrationale Funktion dritten Grades existieren, welche die Forderungen erfüllt.
2.1
Mit Hilfe von Listen für die  - und
- und  -Werte, welche im CAS unter on
-Werte, welche im CAS unter on  List & Spreadsheet erstellt werden, folgt die Durchführung der kubischen Regression wie folgt:
List & Spreadsheet erstellt werden, folgt die Durchführung der kubischen Regression wie folgt:
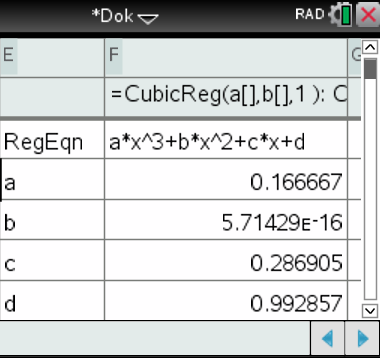 Die Methode der Regression liefert somit die Funktion
Die Methode der Regression liefert somit die Funktion 



Menu  Statistik
Statistik  1: statistische Berechnung
1: statistische Berechnung  7: Kubische Regression
7: Kubische Regression  x-Liste: a[], y-Liste: b[]
x-Liste: a[], y-Liste: b[]  ok
Der CAS liefert folgende Werte:
ok
Der CAS liefert folgende Werte:





2.2
Das Volumenintegral bei Rotation um die  -Achse im Intervall
-Achse im Intervall ![\([a; b]\)](https://mathjax.schullv.de/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3?color=5a5a5a) ist beschrieben durch folgende Gleichung:
ist beschrieben durch folgende Gleichung:

 Zunächst wird der Funktionsterm von
Zunächst wird der Funktionsterm von  unter on
unter on  Graphs eingegeben. Anschließend wird im CAS wie folgt von
Graphs eingegeben. Anschließend wird im CAS wie folgt von  bis
bis  integriert:
integriert:
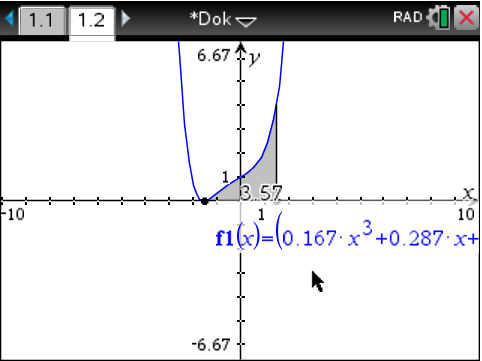
Menu  Graph analysieren
Graph analysieren  7: Integral
7: Integral  untere Schranke: $-1,5
untere Schranke: $-1,5 \rightarrow$ ENTER
\rightarrow$ ENTER  obere Schranke: $1,5
obere Schranke: $1,5 \rightarrow$ ENTER
Nach Multiplikation des Werts des Integrals mit
\rightarrow$ ENTER
Nach Multiplikation des Werts des Integrals mit  folgt für das Volumen:
folgt für das Volumen:



3
1. Schritt: Funktionsgleichungen dreimal ableiten
Dreimaliges Ableiten der Funktionenschar  nach
nach  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_t](https://mathjax.schullv.de/950f7d0fe2bf7a827017caa6d99196dd2ff6b35622cef47b4dda1d18961fefc6?color=5a5a5a) 2. Schritt: Zeigen, dass es nur einen Wendepunkt gibt
Zunächst wird die notwendige Bedingung für einen Wendepunkt überprüft:
Überprüfung des hinreichenden Kriteriums für eine Wendestelle liefert weiter:
Die Funktion
2. Schritt: Zeigen, dass es nur einen Wendepunkt gibt
Zunächst wird die notwendige Bedingung für einen Wendepunkt überprüft:
Überprüfung des hinreichenden Kriteriums für eine Wendestelle liefert weiter:
Die Funktion  hat also genau einen Wendepunkt, und zwar an der Stelle
hat also genau einen Wendepunkt, und zwar an der Stelle  mit dem Funktionswert
mit dem Funktionswert 


 3. Schritt: Krümmungsverhalten bestimmen
Da die dritte Ableitung am Wendepunkt wie oben berechnet größer Null ist, erfolgt an dem Wendepunkt eine Änderung der Krümmung von rechts nach links.
3. Schritt: Krümmungsverhalten bestimmen
Da die dritte Ableitung am Wendepunkt wie oben berechnet größer Null ist, erfolgt an dem Wendepunkt eine Änderung der Krümmung von rechts nach links.
4.1
1. Schritt: Funktionsgleichung  aufstellen
Erstellen zweier Listen für die
aufstellen
Erstellen zweier Listen für die  - und
- und  -Werte der beiden Punkte liefert die Variablen der allgemeinen Funktionsgleichung
-Werte der beiden Punkte liefert die Variablen der allgemeinen Funktionsgleichung  im CAS wie folgt:
im CAS wie folgt:
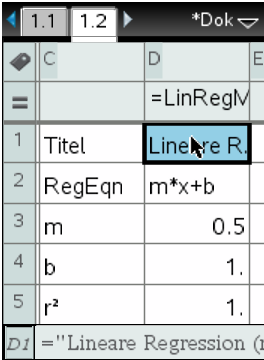 Die Funktion
Die Funktion  hat also folgende Funktionsgleichung:
hat also folgende Funktionsgleichung:
 2. Schritt: Mantelfläche nach Methode A berechnen
Mit Hilfe der ersten Ableitung
2. Schritt: Mantelfläche nach Methode A berechnen
Mit Hilfe der ersten Ableitung  folgt:
folgt:


 Eingabe des Terms unterhalb des Integrals in den CAS und Integrieren von den Grenzen
Eingabe des Terms unterhalb des Integrals in den CAS und Integrieren von den Grenzen  bis
bis  liefert multipliziert mit
liefert multipliziert mit 

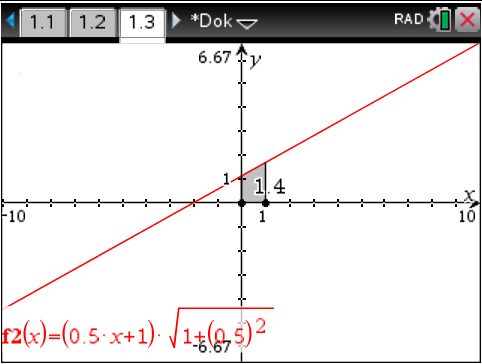 3. Schritt: Mantelfläche nach Methode B berechnen
Für den Kegelstumpf aus dieser Aufgabe sind die Werte für die beiden Radien die
3. Schritt: Mantelfläche nach Methode B berechnen
Für den Kegelstumpf aus dieser Aufgabe sind die Werte für die beiden Radien die  -Werte der beiden Punkte
-Werte der beiden Punkte  und
und  das heißt es gilt
das heißt es gilt  und
und  Weiter folgt die Länge der Mantellinie
Weiter folgt die Länge der Mantellinie  als die Länge der Verbindungslinie der Punkte
als die Länge der Verbindungslinie der Punkte  und
und  Insgesamt folgt damit für die Mantelfläche:
Insgesamt folgt damit für die Mantelfläche:







 4. Schritt: Vergleich der Ergebnisse
Die Ergebnisse der Methoden
4. Schritt: Vergleich der Ergebnisse
Die Ergebnisse der Methoden  und
und  sind identisch.
sind identisch.
Menu  Statistik
Statistik  1: statistische Berechnung
1: statistische Berechnung  3: Lineare Regression
3: Lineare Regression  x-Liste: a[], y-Liste: b[]
x-Liste: a[], y-Liste: b[]  ok
Für die Variablen folgt dann:
ok
Für die Variablen folgt dann:




4.2
Der CAS liefert für die erste Ableitung der Funktion  folgendes:
folgendes:

 Einsetzen in die Formel aus Methode A und Berechnung des Integrals mit dem CAS liefert als Wert für die Mantellinie, nach Multiplikation mit
Einsetzen in die Formel aus Methode A und Berechnung des Integrals mit dem CAS liefert als Wert für die Mantellinie, nach Multiplikation mit 

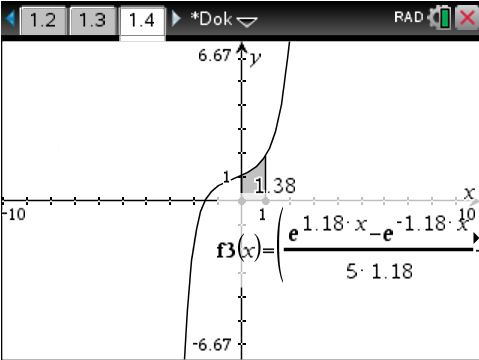 Verglichen mit dem Wert
Verglichen mit dem Wert  aus Aufgabe 4.1 ist das hier berechnete Ergebnis um
aus Aufgabe 4.1 ist das hier berechnete Ergebnis um  geringerer.
geringerer.

1.1
Zwischen den Punkten  und
und  weist der Graph eine Rechtskrümmung auf. Vom Punkt
weist der Graph eine Rechtskrümmung auf. Vom Punkt  bis zum Punkt
bis zum Punkt  existiert allerdings eine Linkskrümmung. Es handelt sich bei
existiert allerdings eine Linkskrümmung. Es handelt sich bei  somit um einen Wendepunkt und die ganzrationale Funktion muss damit mindestens Grad drei haben.
somit um einen Wendepunkt und die ganzrationale Funktion muss damit mindestens Grad drei haben.
1.2
Eine ganzrationale Funktion  dritten Grades hat die allgemeine Form
dritten Grades hat die allgemeine Form  und soll die Punkte
und soll die Punkte  ,
,  und
und  durchlaufen, wobei
durchlaufen, wobei  ein Wendepunkt ist.
ein Wendepunkt ist.
Mit Hilfe des CAS folgt, dass die zweite Ableitung von durch
durch  gegeben ist. Mit dem notwendingen Kriterium für Wendestellen ergibt sich folgendes Gleichungssystem:
Mit Hilfe der folgenden Befehle wird das Gleichungssystem nun mit dem CAS gelöst:
gegeben ist. Mit dem notwendingen Kriterium für Wendestellen ergibt sich folgendes Gleichungssystem:
Mit Hilfe der folgenden Befehle wird das Gleichungssystem nun mit dem CAS gelöst:
 Mit den erhaltenen Variablen
Mit den erhaltenen Variablen  und
und  folgt für die gesuchte Funktion
folgt für die gesuchte Funktion  damit:
damit:




Mit Hilfe des CAS folgt, dass die zweite Ableitung von
solve({lin. Gleichungen}, {Variablen})  ENTER
ENTER

1.3
Einsetzen des Punktes  in die in der vorherigen Teilaufgabe bestimmten Funktion liefert:
in die in der vorherigen Teilaufgabe bestimmten Funktion liefert:





 Der Punkt aus der Wertetabelle liegt nicht auf
Der Punkt aus der Wertetabelle liegt nicht auf  somit kann keine ganzrationale Funktion dritten Grades existieren, welche die Forderungen erfüllt.
somit kann keine ganzrationale Funktion dritten Grades existieren, welche die Forderungen erfüllt.
2.1
Mit Hilfe von Listen für die  - und
- und  -Werte, welche im CAS unter MENU
-Werte, welche im CAS unter MENU  Statistics erstellt werden, folgt die Durchführung der kubischen Regression wie folgt:
Statistics erstellt werden, folgt die Durchführung der kubischen Regression wie folgt:
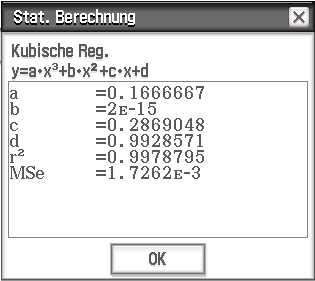 Die Methode der Regression liefert somit die Funktion
Die Methode der Regression liefert somit die Funktion 



Calc  Regression
Regression  Cubic Reg
Cubic Reg  OK
Der CAS liefert folgende Werte:
OK
Der CAS liefert folgende Werte:





2.2
Das Volumenintegral bei Rotation um die  -Achse im Intervall
-Achse im Intervall ![\([a; b]\)](https://mathjax.schullv.de/55d9c86ce052c8cc565dcfb2a42d040a408cd01e6029a75d99c52b506b61c5b3?color=5a5a5a) ist beschrieben durch folgende Gleichung:
ist beschrieben durch folgende Gleichung:

 Zunächst wird der Funktionsterm von
Zunächst wird der Funktionsterm von  unter MENU
unter MENU  Graph & Table eingegeben. Anschließend wird im CAS wie folgt von
Graph & Table eingegeben. Anschließend wird im CAS wie folgt von  bis
bis  integriert:
integriert:
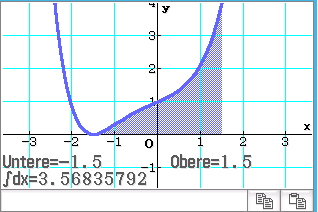
Graph-Icon  Analysis
Analysis  G-Solve
G-Solve  Integral $\rightarrow
Integral $\rightarrow \displaystyle\int\;\mathrm dx
\displaystyle\int\;\mathrm dx \rightarrow$ lower:
\rightarrow$ lower:  , upper: $1,5
, upper: $1,5 \rightarrow$ OK
Nach Multiplikation des Werts des Integrals mit
\rightarrow$ OK
Nach Multiplikation des Werts des Integrals mit  folgt für das Volumen:
folgt für das Volumen:



3
1. Schritt: Funktionsgleichungen dreimal ableiten
Dreimaliges Ableiten der Funktionenschar  nach
nach  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_t](https://mathjax.schullv.de/950f7d0fe2bf7a827017caa6d99196dd2ff6b35622cef47b4dda1d18961fefc6?color=5a5a5a) 2. Schritt: Zeigen, dass es nur einen Wendepunkt gibt
Zunächst wird die notwendige Bedingung für einen Wendepunkt überprüft:
Überprüfung des hinreichenden Kriteriums für eine Wendestelle liefert weiter:
Die Funktion
2. Schritt: Zeigen, dass es nur einen Wendepunkt gibt
Zunächst wird die notwendige Bedingung für einen Wendepunkt überprüft:
Überprüfung des hinreichenden Kriteriums für eine Wendestelle liefert weiter:
Die Funktion  hat also genau einen Wendepunkt, und zwar an der Stelle
hat also genau einen Wendepunkt, und zwar an der Stelle  mit dem Funktionswert
mit dem Funktionswert 


 3. Schritt: Krümmungsverhalten bestimmen
Da die dritte Ableitung am Wendepunkt wie oben berechnet größer Null ist, erfolgt an dem Wendepunkt eine Änderung der Krümmung von rechts nach links.
3. Schritt: Krümmungsverhalten bestimmen
Da die dritte Ableitung am Wendepunkt wie oben berechnet größer Null ist, erfolgt an dem Wendepunkt eine Änderung der Krümmung von rechts nach links.
4.1
1. Schritt: Funktionsgleichung  aufstellen
Erstellen zweier Listen für die
aufstellen
Erstellen zweier Listen für die  - und
- und  -Werte der beiden Punkte liefert die Variablen der allgemeinen Funktionsgleichung
-Werte der beiden Punkte liefert die Variablen der allgemeinen Funktionsgleichung  im CAS wie folgt:
im CAS wie folgt:
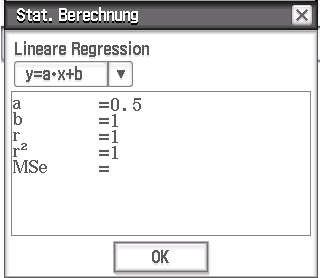 Die Funktion
Die Funktion  hat also folgende Funktionsgleichung:
hat also folgende Funktionsgleichung:
 2. Schritt: Mantelfläche nach Methode A berechnen
Mit Hilfe der ersten Ableitung
2. Schritt: Mantelfläche nach Methode A berechnen
Mit Hilfe der ersten Ableitung  folgt:
folgt:


 Eingabe des Terms unterhalb des Integrals in den CAS und Integrieren von den Grenzen
Eingabe des Terms unterhalb des Integrals in den CAS und Integrieren von den Grenzen  bis
bis  liefert multipliziert mit
liefert multipliziert mit 

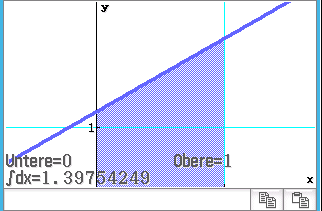 3. Schritt: Mantelfläche nach Methode B berechnen
Für den Kegelstumpf aus dieser Aufgabe sind die Werte für die beiden Radien die
3. Schritt: Mantelfläche nach Methode B berechnen
Für den Kegelstumpf aus dieser Aufgabe sind die Werte für die beiden Radien die  -Werte der beiden Punkte
-Werte der beiden Punkte  und
und  das heißt es gilt
das heißt es gilt  und
und  Weiter folgt die Länge der Mantellinie
Weiter folgt die Länge der Mantellinie  als die Länge der Verbindungslinie der Punkte
als die Länge der Verbindungslinie der Punkte  und
und  Insgesamt folgt damit für die Mantelfläche:
Insgesamt folgt damit für die Mantelfläche:







 4. Schritt: Vergleich der Ergebnisse
Die Ergebnisse der Methoden
4. Schritt: Vergleich der Ergebnisse
Die Ergebnisse der Methoden  und
und  sind identisch.
sind identisch.
Calc  Regression
Regression  Linear Reg
Linear Reg  OK
Für die Variablen folgt dann:
OK
Für die Variablen folgt dann:




4.2
Der CAS liefert für die erste Ableitung der Funktion  folgendes:
folgendes:

 Einsetzen in die Formel aus Methode A und Berechnung des Integrals mit dem CAS liefert als Wert für die Mantellinie, nach Multiplikation mit
Einsetzen in die Formel aus Methode A und Berechnung des Integrals mit dem CAS liefert als Wert für die Mantellinie, nach Multiplikation mit 

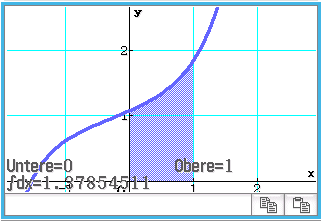 Verglichen mit dem Wert
Verglichen mit dem Wert  aus Aufgabe 4.1 ist das hier berechnete Ergebnis um
aus Aufgabe 4.1 ist das hier berechnete Ergebnis um  geringerer.
geringerer.
