C2.1 - Stochastik

In einem Restaurant können die Gäste beim Bestellen eines Salattellers zwischen einem Essig-Öl-Dressing und einem Joghurtdressing wählen.

An einem bestimmten Tag werden $15 \;\%$ der Salatteller von Kindern bestellt, wobei $90 \; \%$ dieser Kinder das Joghurtdressing wählen. Von den übrigen Gästen (Erwachsene), die einen Salatteller bestellen, wählen $70 \%$ das Joghurtdressing.

Betrachtet werden folgende Ereignisse:

$K:$ Der Salatteller wird von einem Kind bestellt.

$J:$ Für den bestellten Salatteller wird das Joghurtdressing gewählt.

1.1

Zeige rechnerisch mit Angabe eines vollständig beschrifteten Baumdiagramms, dass insgesamt für $73 \;\%$ der bestellten Salatteller das Joghurtdressing gewählt wird.

(4 BE)

1.2

Berechne den Anteil der Kinder unter den Gästen, die für den bestellten Salatteller das Joghurtdressing wählen.

(2 BE)

1.3

Gib die Wahrscheinlichkeiten $P_K(J), P_{\overline{K}}(J)$ und $P(J)$ an.

Erläutere im Sachzusammenhang, dass man aus $P_K(J) \neq P_{\overline{K}}(J)$ auch $P_K(J) \neq P(J)$ folgern kann.

(3 BE)

$35 \;\%$ der Personen eines Landes kennen ein bestimmtes Olivenölprodukt. Im Folgenden werden ausschließlich Personen dieses Landes betrachtet.

2.1

Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:

$E_1:$ Von 40 zufällig ausgewählten Personen kennen genau 10 das Produkt.

$E_2:$ Von 100 zufällig ausgewählten Personen kennen mindestens 29, aber höchstens 37 das Produkt.

(5 BE)

2.2

Nach einer Werbeaktion im Radio besteht die Vermutung, dass der Bekanntheitsgrad des Produkts auf über $35 \;\%$ gestiegen ist. Hierzu sollen 200 zufällig ausgewählte Personen befragt werden.

2.2.1

Entwickle einen Hypothesentest auf einem Signifikanzniveau von $5 \; \%$ und formuliere eine Entscheidungsregel im Sachzusammenhang.

(6 BE)

2.2.2

Bestimme die Wahrscheinlichkeit des Fehlers 2. Art für den Fall, dass der Bekanntheitsgrad des Produkts tatsächlich auf $45 \; \%$ gestiegen ist.

(3 BE)

2.2.3

In Abbildung 1 und 2 sind für den betrachteten Hypothesentest die Wahrscheinlichkeiten für das Annehmen und für das Verwerfen der Hypothese $H_0$ in Abhängigkeit von der wahren Wahrscheinlichkeit $p$ dargestellt. Beide Graphen werden an der Stelle $p=0,35$ jeweils in zwei Abschnitte geteilt.

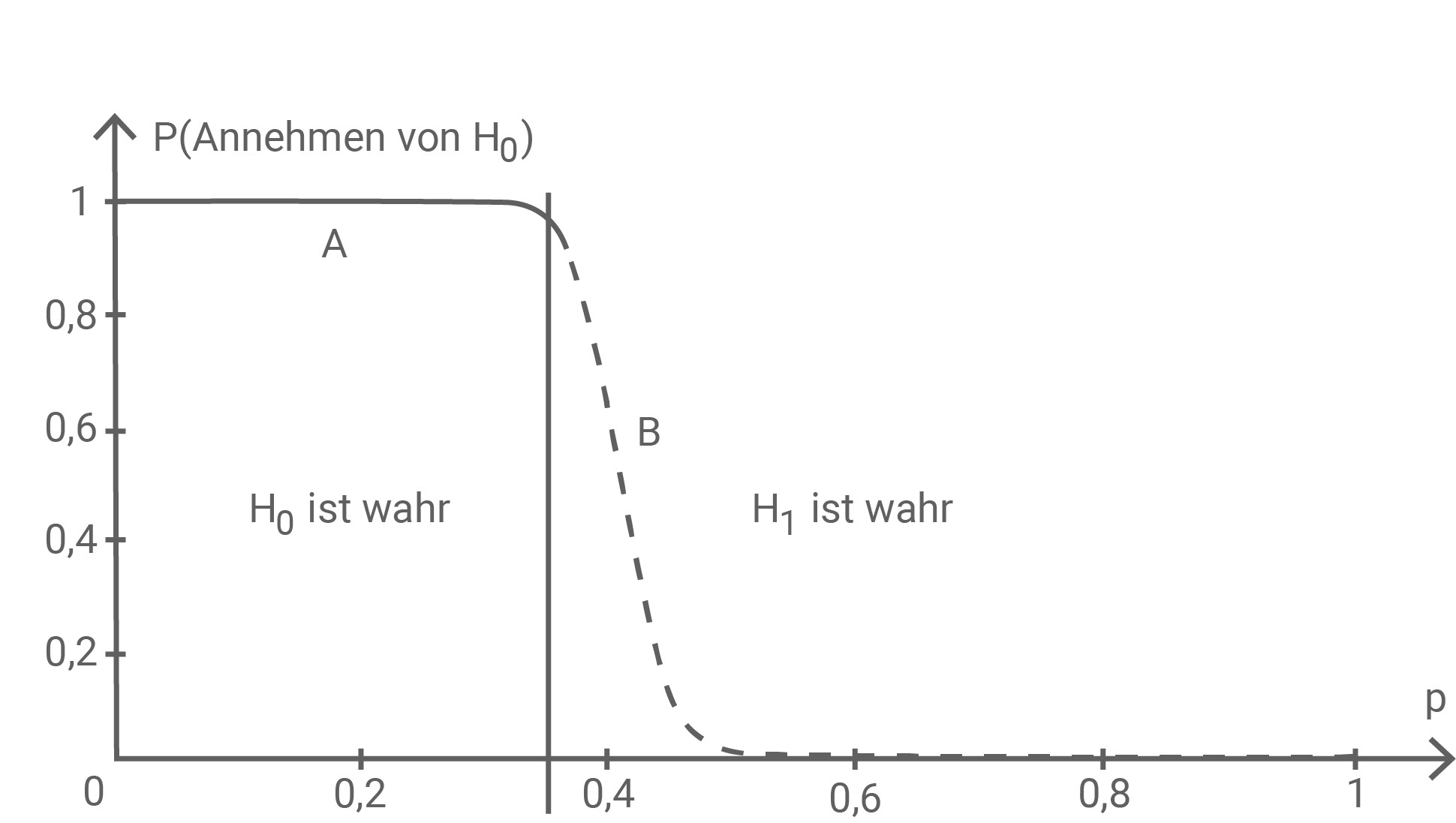
Annahmebereich Nullhypothese Olivenoel Hessen Abi 2023

Abbildung 1

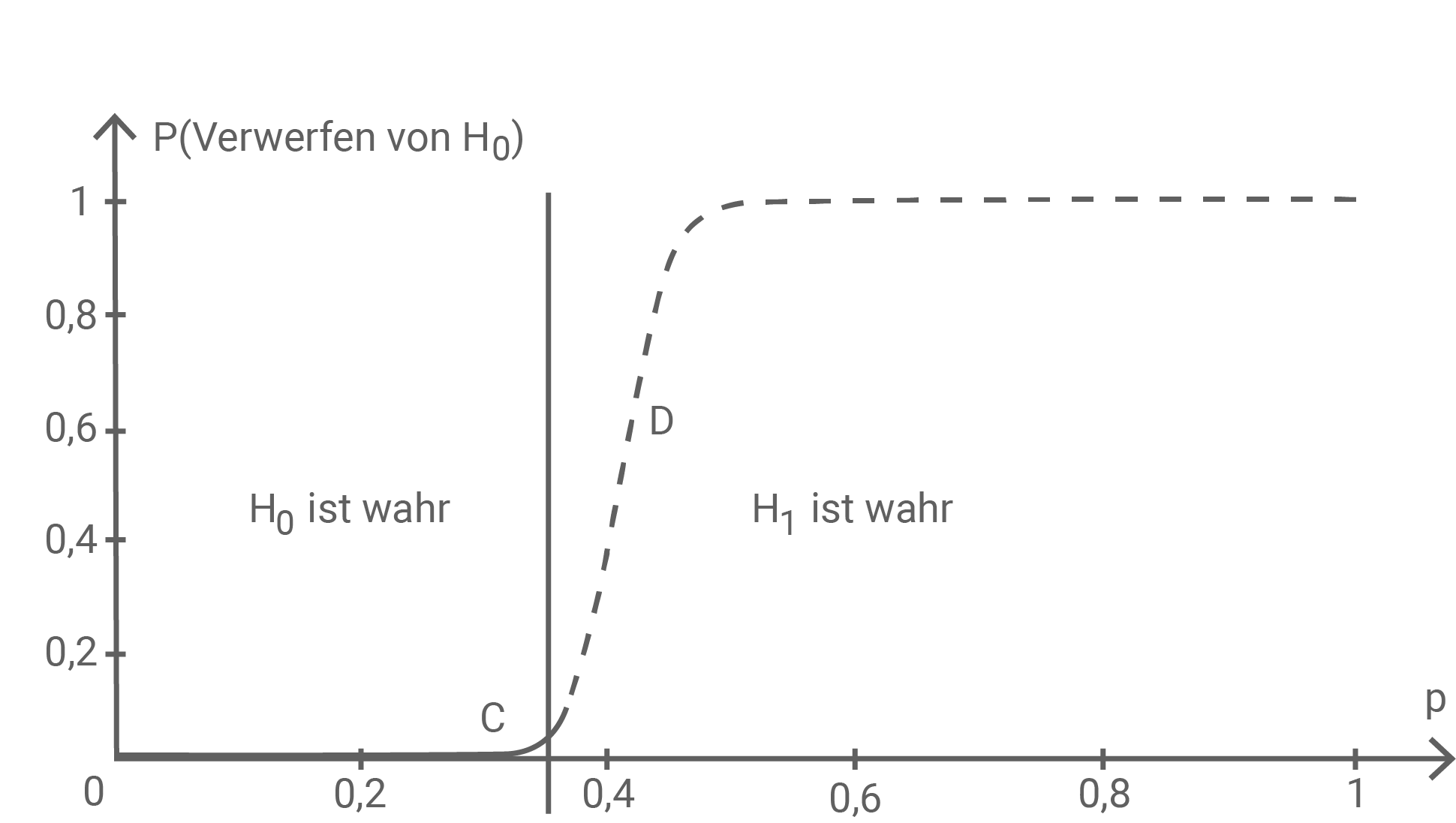Verwerfen der Nullhypothese Olivenoel Hessen Abi 2023

Abbildung 2

Für alle Werte von $p,$ die in den Abschnitten $A$ und $C$ liegen, ist die Hypothese $H_0$ wahr, wohingegen für alle Werte von $p,$ die in den Abschnitten $B$ und $D$ liegen, die Hypothese $H_1$ wahr ist.

Gib zu den Wahrscheinlichkeiten $\text{I},$ $\text{II},$ $\text{III},$ $\text{IV}$ jeweils den Buchstaben des zugehörigen Abschnitts an.

$\text{I}: \quad$ Die Wahrscheinlichkeit $\alpha (p),$ den Fehler 1. Art zu begehen

$\text{II}: \quad$ Die Wahrscheinlichkeit $1-\alpha(p),$ den Fehler 1. Art nicht zu begehen

$\text{III}: \quad$ Die Wahrscheinlichkeit $\beta(p),$ den Fehler 2. Art zu begehen

$\text{IV}: \quad$ Die Wahrscheinlichkeit $1-\beta(p),$ den Fehler 2. Art nicht zu begehen

(2 BE)

Ein Unternehmen stellt Olivenöl her und füllt es in Flaschen ab. Laut Aufdruck beträgt die Füllmenge jeder Flasche $600 \mathrm{ml}.$

3.1

Die Flaschen werden in Kartons verpackt; jeder Karton enthält zwölf Flaschen. Ein Karton gilt als fehlerhaft, wenn mehr als eine Flasche weniger als $600 \;\mathrm{ml}$ Öl enthält.

Für jede Flasche beträgt die Wahrscheinlichkeit dafür, dass sie weniger als $600 \;\mathrm{ml}$ Öl enthält, $1,5 \; \%$ .

3.1.1

Die Rechnung $0,985^{12} \approx 83,4 \;\%$ stellt im Sachzusammenhang die Lösung einer Aufgabe dar.

Formuliere eine passende Aufgabenstellung und erläutere den Ansatz der Rechnung.

(3 BE)

3.1.2

An einen Supermarkt wird regelmäßig die gleiche Anzahl von Flaschen geliefert. Dabei enthalten im Mittel mehr als 780 Flaschen mindestens $600 \;\mathrm{ml}$ Öl.

Ermittle, wie viele Flaschen mindestens geliefert werden.

(3 BE)

3.1.3

Ein Supermarkt erhält eine Lieferung von 150 Kartons.

Bestimme die Wahrscheinlichkeit dafür, dass mehr als $3 \;\%$ der Kartons fehlerhaft sind.

(4 BE)

3.2

Die Füllmenge der Flaschen soll als normalverteilt mit einem Erwartungswert von $600,5 \;\mathrm{ml}$ und einer Standardabweichung von $0,23 \;\mathrm{ml}$ angenommen werden.

3.2.1

Eine Flasche wird zufällig ausgewählt.

Ermittle für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:

$A:$ Die Flasche enthält mehr als $601 \;\mathrm{ml}$ Öl.

$B:$ Die Füllmenge der Flasche weicht höchstens um $0,5\;\mathrm{ml}$ vom Erwartungswert ab.

(3 BE)

3.2.2

Die Füllmenge einer Flasche ist nie negativ. Die Dichtefunktion der Normalverteilung, die zur Beschreibung der Füllmenge der Flaschen verwendet wird, ist jedoch auch für negative reelle Zahlen definiert und nimmt dabei ausschließlich positive Werte an.

Begründe, dass die Verwendung der Normalverteilung dennoch sinnvoll ist.

(2 BE)

3.2.3

Das Unternehmen möchte die Wahrscheinlichkeit dafür, dass eine Flasche weniger als $600 \;\mathrm{ml}$ Öl enthält, verringern. Für die nötige Änderung der Maschine, die die Flaschen befüllt, gibt es zwei Vorschläge:

Vorschlag 1: Die eingestellte Füllmenge von $600,5 \;\mathrm{ml}$ wird erhöht.

Vorschlag 2: Die Genauigkeit, mit der die eingestellte Füllmenge von $600,5 \;\mathrm{ml}$ erreicht wird, wird erhöht.

Die Abbildungen 3 und 4 zeigen jeweils den Graphen der Dichtefunktion, die vor der Änderung der Maschine die Füllmenge der Flaschen beschreibt.

Skizziere in der Abbildung 3 den Graphen einer Dichtefunktion, die sich aus dem Vorschlag 1 ergeben könnte, und in der Abbildung 4 den Graphen einer Dichtefunktion, die zum Vorschlag 2 passt.

Begründe für jeden Vorschlag mithilfe des skizzierten Graphen, dass damit das Ziel des Unternehmens erreicht wird.

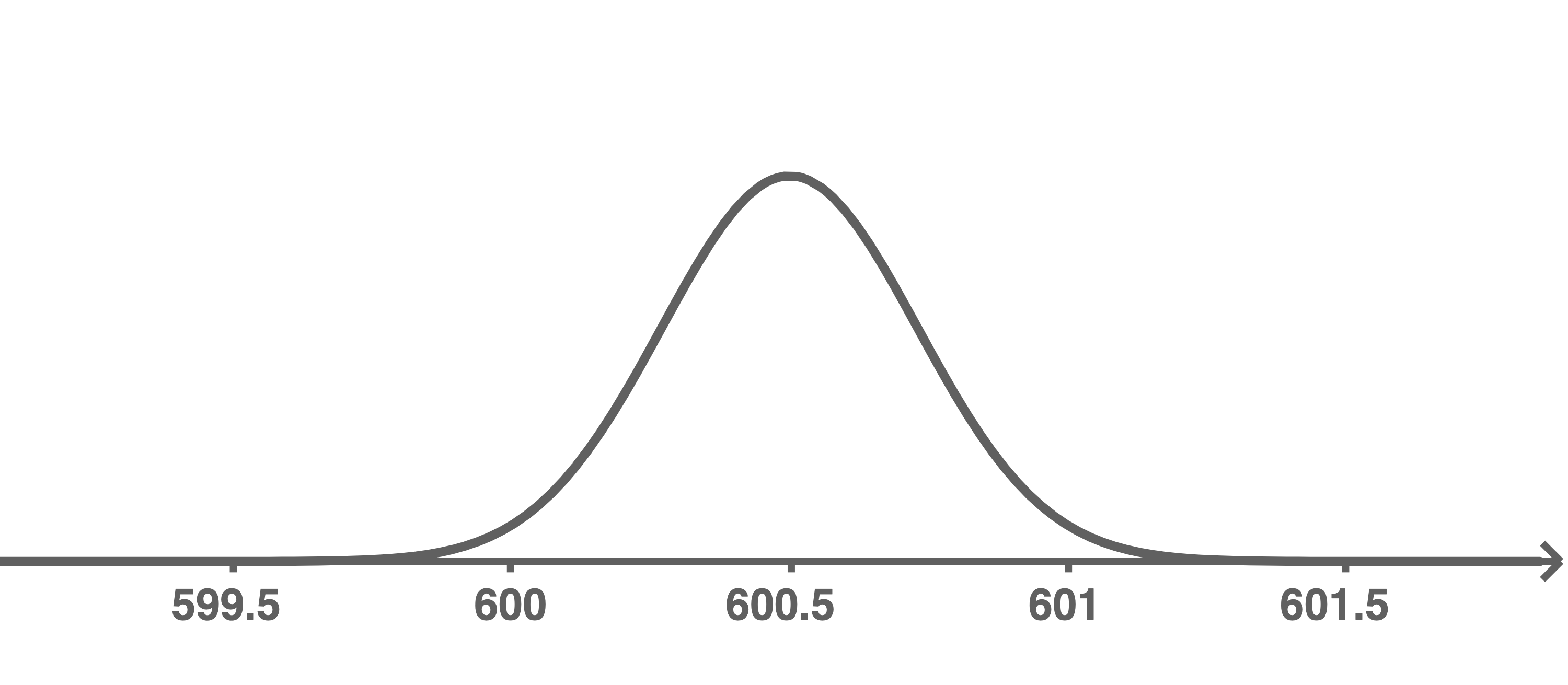
Normalverteilung Oel Flaschen BW Mathe Abi

Abbildung 3

Abbildung 4

(6 BE)

3.3

Jede Flasche wird mit einem Anhänger versehen. Die Anhänger gibt es mit $n$ verschiedenen Motiven. Für jede Flasche wird eines dieser Motive zufällig ausgewählt.

Die Wahrscheinlichkeit dafür, dass bei $n$ zufällig ausgewählten Flaschen alle Motive verschieden sind, ist kleiner als $1 \;\%.$

Ermittle den kleinsten möglichen Wert von $n.$

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Baumdiagramm angeben

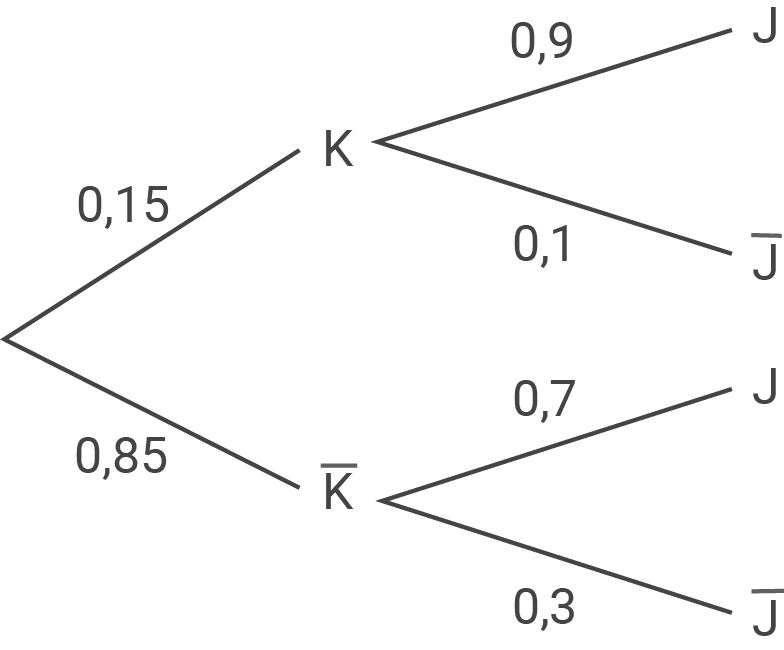Salatdressing Joghurt Stochastik Hessen Abi Baumdiagramm

Aussage nachweisen

$\begin{array}[t]{rll} P(J)&=& 0,15\cdot 0,9+0,85\cdot 0,7 &\ \\[5pt] &=& 0,73 & \\[5pt] &=& 73 \; \% \end{array}$

1.2

$\begin{array}[t]{rll} P_J(K)&=& \dfrac{P(J \cap K)}{P(J)}&\\[5pt] &=& \dfrac{0,15\cdot 0,9}{0,73}&\\[5pt] &\approx& 0,185 &\\[5pt] &=& 18,5 \;\% \end{array}$

1.3

Wahrscheinlichkeiten angeben

$P_K(J)=0,9$

$P_{\overline{K}}(J)=0,7$

$P(J)=0,73$

Folgerungen erläutern

Die Ungleichung $P_K(J)\neq P_{\overline{K}}(J)$ bedeutet, dass der Anteil der Kinder, die das Joghurtdressing wählen, ungleich dem Anteil der Erwachsenen ist, die das Joghurtdressing wählen.

Würden sowohl Kinder als auch Erwachsene jeweils zum gleichen Anteil das Joghurtdressing wählen, so würde gelten:

$P(J)=P_K(J)=P_{\overline{K}}(J)$

Wenn die Erwachsenen jedoch zu einem höheren bzw. geringeren Anteil als die Kinder das Joghurtdressing wählen, so wird auch $P(J)$ größer bzw. kleiner als $P_K(J).$

2.1

Ereignis 1

$X$ beschreibt die Anzahl der Personen, die das Olivenölprodukt kennen und wird mit $n=40$ und $p=0,35$ als binomialverteilt betrachtet.

$\begin{array}[t]{rll} P(E_1)&=& P(X=10)&\quad \scriptsize \mid\; CAS \\[5pt] &\approx& 0,057 \end{array}$

Ereignis 2

$X$ beschreibt die Anzahl der Personen, die das Olivenölprodukt kennen und wird mit $n=100$ und $p=0,35$ als binomialverteilt betrachtet.

Rechenweg anzeigen

$P(E_2) \approx 0,617$

2.2.1

1. Schritt: Nullhypothese definieren

Betrachtet wird die Zufallsvariable $X,$ die die Anzahl der befragten Personen beschreibt, die das Produkt kennen. $X$ kann als binomialverteilt mit $n=200$ und $p$ angenommen werden.

Es wird folgende Nullhypothese betrachtet:

$H_0:$ Der Anteil der Personen, die das Olivenölprodukt kennen, beträgt höchstens $35\,\%: p\leq 0,35$

2. Schritt: Ablehnungsbereich bestimmen

Es ist das kleinste $k$ gesucht, sodass folgendes gilt:

$P(X\geq k)\lt 0,05$

Umformungen anzeigen

Systematisches Ausprobieren mit dem CAS liefert:

$P(X\leq 80)\approx 0,939$

$P(X\leq 81)\approx 0,955$

Somit folgt der Ablehnungsbereich mit $\overline{A}=[82;200].$

3. Schritt: Entscheidungsregel formulieren

Geben mindestens 82 der 200 befragten Besucher an, das Produkt zu kennen, so wird die Nullhypothese abgelehnt und angenommen, dass mehr als $35\,\%$ der Personen das Olivenölprodukt kennen.

2.2.2

$X$ beschreibt die Anzahl der Personen, die das Olivenölprodukt kennen, und ist binomialverteilt mit $n=200$ und $p=0,45.$

$P(X\leq 81)\approx 0,113=11,3\,\%$

Die Wahrscheinlichkeit für den Fehler 2. Art bei einer tatsächlichen Erhöhung des Anteils der Personen, die das Olivenölprodukt kennen, auf $45\,\%$ beträgt somit ungefähr $11,3\,\%.$

2.2.3

$\text{I:}$ Der Fehler 1. Art ist eine irrtümliche Ablehnung der Nullhypothese. $\alpha (p)$ wird somit in Abschnitt $C$ dargestellt.

$\text{II:}$ Der Fehler 1. Art wird nicht begangen, wenn die Nullhypothese wahr ist und nicht abgelehnt wird. Dies entspricht Abschnitt $A.$

$\text{III:}$ Beim Fehler 2. Art wird die Nullhypothese nicht abgelehnt obwohl sie nicht wahr ist. $\beta(p)$ wird somit in Abschnitt $B$ dargestellt.

$\text{IV:}$ Der Fehler 2. Art wird nicht begangen, wenn die Nullhypothese nicht wahr ist und abgelehnt wird. Dies entspricht Abschnitt $D.$

3.1.1

Aufgabenstellung formulieren

„Es wird ein Karton zufällig ausgewählt. Berechne die Wahrscheinlichkeit dafür, dass jede Flasche aus dem Karton mindestens $600\,\text{ml}$ Öl enthält."

Ansatz erläutern

Wahrscheinlichkeit dafür, dass eine Flasche mindestens $600\,\text{ml}$ enthält:

$1-0,015=0,985$

Wahrscheinlichkeit dafür, dass alle 12 Flaschen aus einem Karton mindestens $600\,\text{ml}$ enthalten:

$0,985^{12}$

3.1.2

Das Mittel von mehr als 780 Flaschen entspricht dem Erwartungswert. Hierbei beschreibt $n$ die Anzahl der gelieferten Flaschen.

Es soll gelten:

$\begin{array}[t]{rll} \mu&\gt& 780& \\[5pt] n\cdot 0,985&\gt& 780&\quad \scriptsize \mid\; :0,985 \\[5pt] n&\gt& 791,9& \\[5pt] \end{array}$

Da die Anzahl der Flaschen eine natürliche Zahl sein muss, gilt $n \gt 792.$

Es werden also mindestens 792 Flaschen geliefert.

3.1.3

$X$ beschreibt die Anzahl der Flaschen in einem Karton, die weniger als $600\,\text{ml}$ enthalten und ist binomialverteilt mit $n=12$ und $p=0,015.$

Mit dem binomcdf-Befehl folgt:

$\begin{array}[t]{rll} P(„\text{fehlerhaft}")&=& P(X \geq 2) \\[5pt] &=& 1- P(X \leq 1)\quad \scriptsize \mid\; CAS \\[5pt] &\approx& 0,013 \end{array}$

$Y$ beschreibt die Anzahl der fehlerhaften Kartons und ist binomialverteilt mit $n=150$ und $p=0,013.$

$3\,\%$ der Kartons entspricht $150\cdot 0,03=4,5.$ Da die Anzahl der Kartons eine natürliche Zahl sein muss und mehr als $3\,\%$ fehlerhaft sein sollen, müssen in diesem Fall also mindestens 5 Kartons fehlerhaft sein.

Es gilt also:

$\begin{array}[t]{rll} P(Y \geq 5) &=& 1-P(Y \leq 4) \\[5pt] &\approx & 0,05 \end{array}$

Die Wahrscheinlichkeit dafür, dass mehr als $3\,\%$ der Kartons fehlerhaft sind, beträgt somit ca. $5\,\%.$

3.2.1

$Z$ beschreibt die Füllmenge der Flasche in $\,\text{ml}$ und ist normalverteilt mit $\mu=600,5$ und $\sigma=0,23.$

Mit dem normalcdf-Befehl des CAS folgt:

Ereignis A

$\begin{array}[t]{rll} P(A)&=& P(Z\gt 601) \\[5pt] &=& 1- P( Z\leq 601) &\quad \scriptsize \mid\; CAS \\[5pt] &\approx& 0,015 \\[5pt] &=& 1,5\,\% \end{array}$

Ereignis B

$\begin{array}[t]{rll} P(B)&=& P(600 \leq Z\leq 601) \\[5pt] &\approx& 0,970 \\[5pt] &=& 97\,\% \end{array}$

3.2.2

Die verwendete Normalverteilung liefert für die negativen Füllmengen so geringe Wahrscheinlichkeiten, dass diese vernachlässigt werden können.

3.2.3

Graphen skizzieren

Mögliche Graphen für die beiden Vorschläge sind beispielsweise:

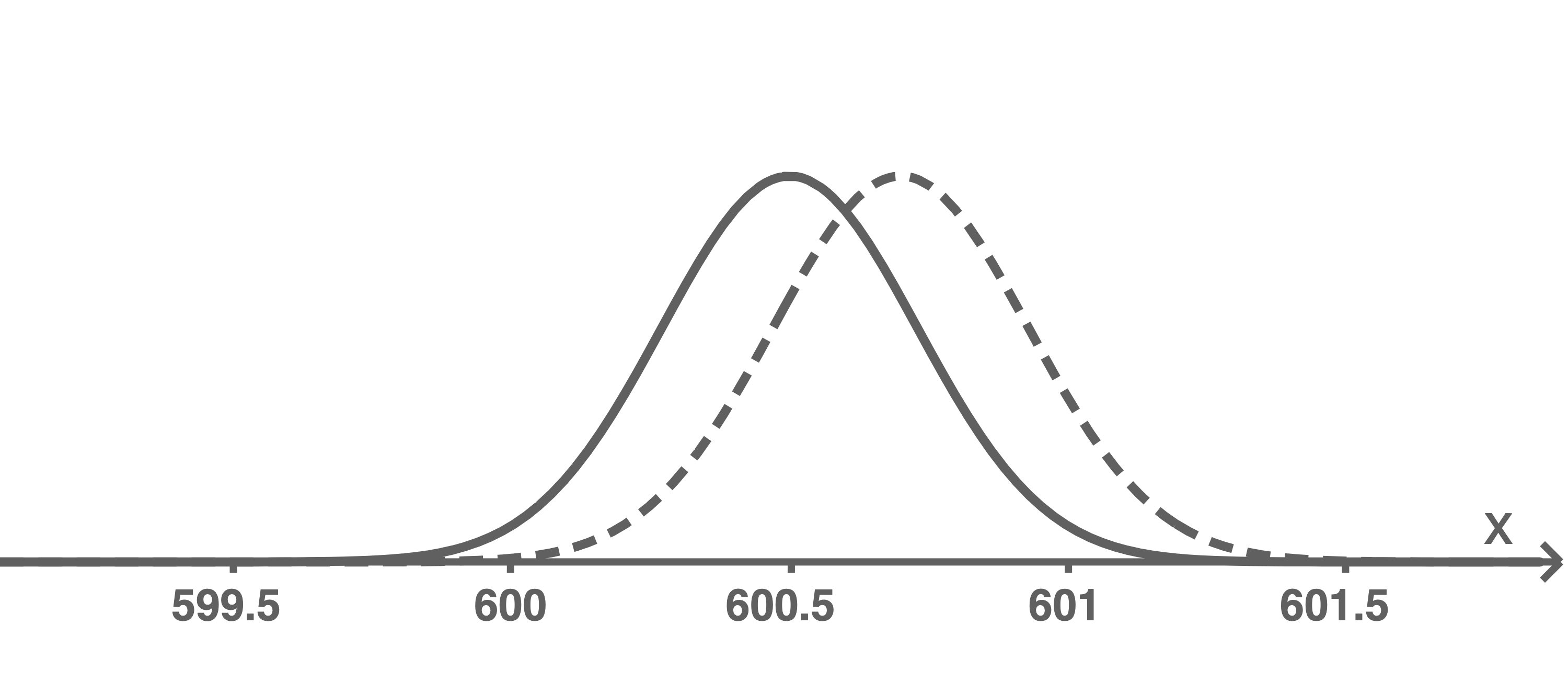
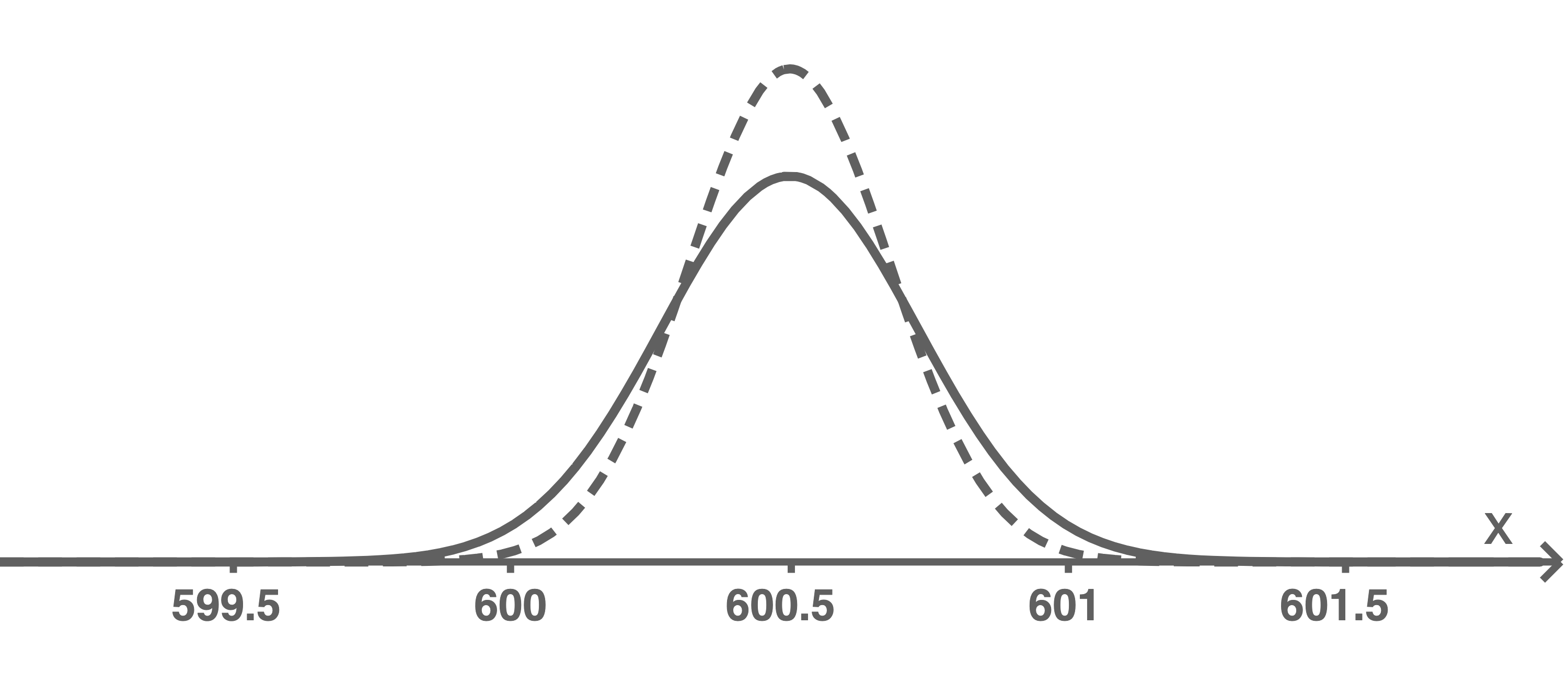Normalverteilung Verschiebung BW Mathe Abi 2023

Abbildung 1

Abbildung 2

Vorschläge begründen

Der Inhalt der Fläche, die für $x \leq 600$ zwischen dem Graphen der Dichtefunktion und der $x$ -Achse eingeschlossen wird, entspricht der Wahrscheinlichkeit dafür, dass eine Flasche weniger als $600\,\text{ml}$ Öl enthält.

Beim ersten Vorschlag wird der Graph der Dichtefunktion auf der $x$ -Achse weiter entlang der positiven $x$ -Achse verschoben, sodass die darunterliegende Fläche für $x \leq 600$ minimiert wird.

Durch das Strecken des Graphen der Dichtefunktion in $y$ -Richtung wird ebenso durch Vorschlag 2 die Fläche für $x \leq 600$ unter dem Graphen reduziert.

Somit erfüllen beide Vorschläge das Ziel, die Wahrscheinlichkeit dafür, dass eine Flasche weniger als $600\,\text{ml}$ Öl enthält, zu verringern.

3.3

Das Vorgehen beschreibt das stochastische Modell „Ziehen mit Zurücklegen und mit Beachtung der Reihenfolge".

Für $n$ verschiedene Motive und $n$ zufällig ausgewählte Flaschen gibt es somit genau $n^n$ mögliche Kombinationen.

Wenn jede Flasche ein unterschiedliches Motiv haben soll, gibt es nach jedem Versehen einer Flasche mit einem Anhänger ein mögliches Motiv weniger für die nächsten Flaschen. Die Anzahl der möglichen Kombinationen entspricht somit $n!.$

Es folgt also:

$P=\dfrac{n!}{n^n}$

Einsetzen verschiedener Werte für $n$ liefert $\dfrac{6!}{6^6}\approx 0,015$ und $\dfrac{7!}{7^7}\approx 0,006.$

Als kleinstmöglicher Wert von $n$ ergibt sich somit $7.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?