C - Stochastik

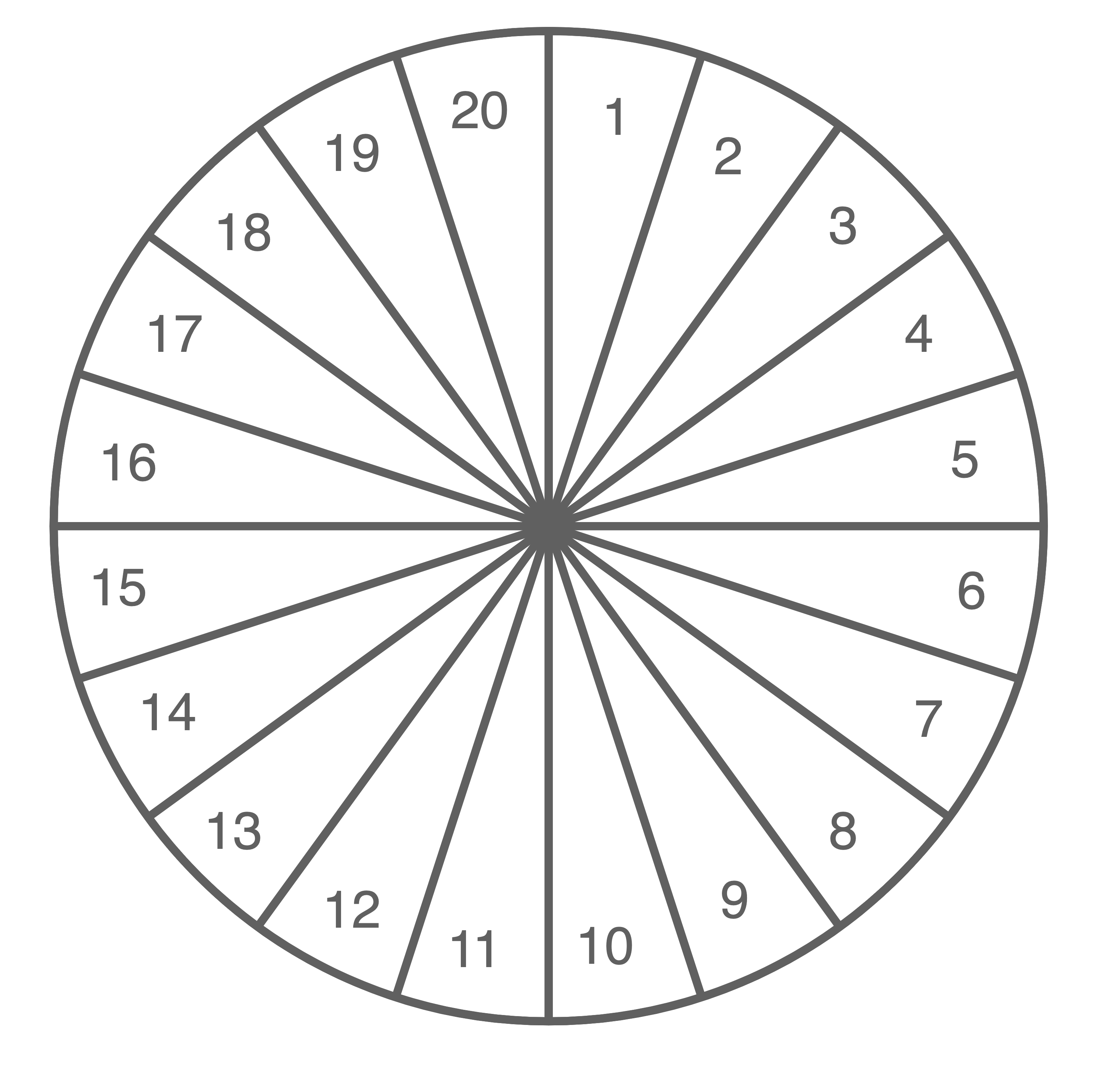
Bei einem Spiel werden kleine Pfeile von einer Position hinter einer Wurflinie aus auf eine kreisförmige Scheibe geworfen. Bleibt der Pfeil in einem Feld stecken, wird dem Spieler die dem Feld zugeordnete Punktzahl gutgeschrieben. Die Scheibe ist dabei in $20$ gleich große Felder unterteilt, welche die Nummern eins bis $20$ tragen (Material 1). Es wird angenommen, dass sich auch bei wiederholten Würfen die Trefferwahrscheinlichkeiten für alle beteiligten Spieler nicht verändern. Darüber hinaus gilt die Annahme, dass die beteiligten Spieler bei jedem Wurf die Scheibe treffen und der Pfeil in einem Feld stecken bleibt.
Für den Spieler $L$ („Laie“) gelte die Annahme, dass er unabhängig davon, auf welches Feld er zielt, alle Felder mit der gleichen Wahrscheinlichkeit trifft.

Material 1

Für den Spieler $K$ („Könner“) ist für den Fall, dass er auf Feld „20“ zielt, ein Ausschnitt aus der zugehörigen Wahrscheinlichkeitsverteilung in der folgenden Tabelle dargestellt.

Feld $\color{#fff}{F}$	$\color{#fff}{P}$ (Feld $\color{#fff}{F}$ wird getroffen)
$17$	$\dfrac{8}{160}$
$18$	$\dfrac{9}{160}$
$19$	$\dfrac{20}{160}$
$20$	$\dfrac{31}{160}$

1.1

Gib sowohl für den Spieler $L$ als auch für den Spieler $K$ die Wahrscheinlichkeit an, dass er beim einmaligen Werfen das Feld „19“ oder das Feld „20“ trifft, wenn er auf Feld „20“ zielt.

(3 BE)

1.2

Erkläre für den Spieler $K$ den folgenden Term und seine einzelnen Bestandteile im Sachzusammenhang und gib das zugehörige Ergebnis an. Geh dabei davon aus, dass der Spieler $K$ auf Feld „20“ gezielt hat.

$\displaystyle\sum\limits_{k=0}^2...$

Term anzeigen

(4 BE)

2.1

Berechne die Anzahl der Würfe, die der Spieler $L$ mindestens benötigt, um mit einer Wahrscheinlichkeit von mindestens $99\,\%$ mindestens einmal das Feld „20“ zu treffen.

(4 BE)

2.2

Ein dritter Spieler zielt ebenfalls auf Feld „20“. Dieser Spieler $M$ („Meister“) trifft das Feld „20“ mit der Wahrscheinlichkeit $p_M.$
Erläutere die im folgenden dargestellten Zeilen und deute den Ansatz $(\text{I})$ und das Ergebnis $(\text{II})$ im Sachzusammenhang:

$(\text{I})$

$1-(1-p_M)^n \geq 0,99$

$(\text{II})$

$n=10 \Rightarrow p_M\geq 0,37$

$n=5 \Rightarrow p_M\geq 0,61$

(5 BE)

Auf der Grundlage der bisherigen Leistungen kann man für den Spieler $M$ von einer Treffsicherheit im Hinblick auf das Feld „20“ von $p_M= 0,7$ ausgehen.

3.1

Ermittle die $2\sigma$ -Umgebung um den Erwartungswert (Material 2) für den Spieler $M,$ wenn die zugehörige Zufallsvariable die Anzahl der Treffer von Feld „20“ bei $100$ Würfen angibt. Beschreibe die Bedeutung dieser $2\sigma$ -Umgebung im Sachzusammenhang.

Material 2
Wenn $\mu$ der Erwartungswert einer binomialverteilten Zufallsvariable $X$ ist und $\sigma$ die zugehörige Standardabweichung, dann gilt (falls $\sigma \gt 3$ ) für die sogenannte $2\sigma$ -Umgebung um den Erwartungswert

Erwartungswert anzeigen

(3 BE)

3.2

Einer der drei Spieler $L, K, M$ wird zufällig ausgewählt. Der Spieler zielt auf das Feld „20“ und wirft einen Pfeil. Berechne die Wahrscheinlichkeit dafür, dass es sich bei dem ausgewählten Spieler um den Spieler $M$ handelt unter der Voraussetzung, dass das Feld „20“ getroffen wird.

(3 BE)

3.3

Da der Spieler $M$ mit seiner Treffsicherheit für das Feld „20“ unzufrieden war, hat er intensive Trainingswochen hinter sich gebracht. Am Ende dieser Trainingswochen ist er davon überzeugt, sich verbessert zu haben. Um seinen Trainingserfolg zu überprüfen, wirft er $200$ Pfeile auf die Scheibe.

3.3.1

Entwickle im Sachzusammenhang eine Entscheidungsregel, mit der der Spieler $M$ anhand der Anzahl der Treffer des Felds „20“ auf einem Signifikanzniveau von $5\,\%$ seinen Trainingserfolg überprüfen kann.

(5 BE)

3.3.2

Bestimme ausgehend von deiner Entscheidungsregel aus Aufgabe 3.3.1 die Wahrscheinlichkeit für einen Fehler 2. Art für den Fall, dass die tatsächliche Treffsicherheit des Spielers $M$ für das Feld „20“ nun bei $78\,\%$ liegt.

(3 BE)

Binomialsummenfunktion

$F_{n;p}(k)=\displaystyle\sum\limits_{i=0}^{k}\begin{pmatrix}n\\ i\end{pmatrix}\cdot p^i \cdot (1-p)^{n-i}$ für $n = 50$

	A	B	C	D	E	F
1	n	p
2	n	k	0,65	0,70	0,75	0,78
3	200	125	0,2511	0,0138	0,0001	0,0000
4		126	0,3001	0,0200	0,0001	0,0000
5		127	0,3531	0,0284	0,0002	0,0000
6		128	0,4093	0,0396	0,0004	0,0000
7		129	0,4675	0,0542	0,0006	0,0000
8		130	0,5266	0,0728	0,0010	0,0000
9		131	0,5852	0,0960	0,0017	0,0000
10		132	0,6421	0,1242	0,0028	0,0001
11		133	0,6961	0,1579	0,0044	0,0001
12		134	0,7463	0,1972	0,0068	0,0002
13		135	0,7918	0,2421	0,0103	0,0004
14		136	0,8323	0,2921	0,0154	0,0007
15		137	0,8673	0,3467	0,0226	0,0012
16		138	0,8971	0,4047	0,0323	0,0020
17		139	0,9217	0,4652	0,0454	0,0032
18		140	0,9416	0,5267	0,0625	0,0052
19		141	0,9574	0,5877	0,0843	0,0081
20		142	0,9695	0,6468	0,1115	0,0124
21		143	0,9787	0,7028	0,1445	0,0185
22		144	0,9854	0,7545	0,1838	0,0272
23		145	0,9903	0,8012	0,2293	0,0391
24		146	0,9936	0,8421	0,2808	0,0549
25		147	0,9959	0,8772	0,3374	0,0756
26		148	0,9975	0,9066	0,3983	0,1018
27		149	0,9985	0,9305	0,4621	0,1343
28		150	0,9991	0,9494	0,5271	0,1734
29		151	0,9995	0,9641	0,5917	0,2193
30		152	0,9997	0,9751	0,6542	0,2717
31		153	0,9998	0,9831	0,7130	0,3301
32		154	0,9999	0,9889	0,7668	0,3933
33		155	1,0000	0,9928	0,8148	0,4597
34		156	1,0000	0,9955	0,8562	0,5277
35		157	1,0000	0,9973	0,8911	0,5952
36		158	1,0000	0,9984	0,9196	0,6604
37		159	1,0000	0,9991	0,9422	0,7214
38		160	1,0000	0,9995	0,9595	0,7768
39		161	1,0000	0,9997	0,9724	0,8257

1.1

Spieler $L$ trifft alle Felder mit der gleichen Wahrscheinlichkeit. Die Wahrscheinlichkeit dafür, dass er das Feld „19“ oder das Feld „20“ trifft, beträgt also:

$P_L(19;20) = \frac{2}{20} = \frac{1}{10} = 10\,\%$

Spieler $K$ trifft mit einer Wahrscheinlichkeit von $\frac{20}{160}$ das Feld „19“ und mit einer Wahrscheinlichkeit von $\frac{31}{160}$ das Feld „20“, wenn er auf das Feld „20“ zielt. Mit der Pfadadditionsregel folgt daher:

$P_K(19;20)= 31,875\,\%$

Rechenweg anzeigen

1.2

Term erläutern

In dem Term $\sum\limits_{k=0}^2 \binom{22}{k}\cdot \left(\frac{31}{160} \right)^k \cdot \left(\frac{129}{160} \right)^{22-k}$ werden die Einzelwahrscheinlichkeiten $\binom{22}{k}\cdot \left(\frac{31}{160} \right)^k \cdot \left(\frac{129}{160} \right)^{22-k}$ für $k = 0,$ $k=1$ und $k=2$ aufaddiert.

Dies sind die Wahrscheinlichkeiten $P(X=k)$ einer binomialverteilten Zufallsgröße $X,$ bei der die Trefferwahrscheinlichkeit $p= \frac{31}{160}$ beträgt und ein Stichprobenumfang von $n = 22$ betrachtet wird.

Im Sachzusammenhang wird mit dem Term also die Wahrscheinlichkeit dafür berechnet, dass der Spieler $K$ in $22$ Versuchen höchstens zweimal das Feld „20“ trifft, wenn er auf das Feld „20“ zielt.

Ergebnis angeben

Mit dem Taschenrechner können die einzelnen Wahrscheinlichkeiten berechnet werden.

Es folgt:

Ergebnis anzeigen

Mit einer Wahrscheinlichkeit von $17,19\,\%$ trifft Spieler $K$ in $22$ Versuchen, in denen er auf das Feld „20“ zielt, höchstens zweimal das Feld „20“.

2.1

Die Zufallsgröße $X_n$ beschreibt, wie oft Spieler $L$ bei $n$ Versuchen das Feld 20 trifft. Diese kann als binomialverteilt mit unbekanntem $n$ und $p= \frac{1}{20} = 0,05$ angenommen werden.

$P(X_n\geq 1)\geq 0,99$

Rechnung anzeigen

Der Spieler $L$ muss folglich mindestens 90 mal Werfen, um mit einer Wahrscheinlichkeit von mindestens $99\,\%$ mindestens einmal das Feld „20“ zu treffen.

2.2

Ansatz $\text{I}$ erläutern

$p_M$ beschreibt die Trefferwahrscheinlichkeit von Spieler $M.$ Der Term $(1-p_M)$ bezeichnet also die Wahrscheinlichkeit dafür, dass Spieler $M$ bei einem Wurf, bei dem er auf das Feld „20“ zielt, nicht trifft.

Der Term $(1-p_M)^n$ gibt also die Wahrscheinlichkeit dafür an, dass der Spieler $M$ von $n$ Versuchen, das Feld „20“ zu treffen, kein einziges mal das Feld „20“ trifft.

Der Term $1-(1-p_M)^n$ gibt folglich die Wahrscheinlichkeit dafür an, dass Spieler $M$ bei $n$ Versuchen nicht $n$ mal nicht trifft, dass er also von $n$ Versuchen höchstens $n-1$ mal nicht trifft bzw. mindestens einmal trifft.

Der Ansatz wurde also so gewählt, dass die Wahrscheinlichkeit dafür, dass Spieler $M$ von $n$ Versuchen mindestens einmal das Feld „20“ trifft, mindestens $99\,\%$ beträgt.

Ergebnis deuten

In Zeile $(\text{II})$ sind dann für $n=10$ und $n=5$ die erforderlichen Trefferwahrscheinlichkeiten angegeben.

Damit also Spieler $M$ in zehn Versuchen mit einer Wahrscheinlichkeit von mindestens $99\,\%$ mindestens einmal das Feld „20“ trifft, muss die Trefferwahrscheinlichkeit von Spieler $M$ mindestens $0,37 = 37\,\%$ betragen.

Damit er in fünf Versuchen mit einer Wahrscheinlichkeit von mindestens $99\,\%$ mindestens einmal das Feld „20“ trifft, muss die Trefferwahrscheinlichkeit von Spieler $M$ mindestens $0,61 = 61\,\%$ betragen.

3.1

$2\sigma$ -Umgebung ermitteln

Die Zufallsgröße $Y$ beschreibt die Anzahl der Treffer von Feld „20“ von Spieler $M$ bei $100$ Würfen.

$Y$ ist binomialverteilt mit $n=100$ und $p=0,7.$

$\begin{array}[t]{rll} \mu&=& n\cdot p \\[5pt] &=& 100 \cdot 0,7 \\[5pt] &=& 70 \\[10pt] \sigma&=& \sqrt{n\cdot p\cdot (1-p)} \\[5pt] &=& \sqrt{100 \cdot 0,7\cdot 0,3} \\[5pt] &=& \sqrt{21} \gt 3 \\[10pt] \end{array}$

Einsetzen in die Angaben aus Material 2 liefert dann wegen $\sigma \gt 3:$

$[70-2\cdot \sqrt{21};70 +2\cdot \sqrt{21}] \approx [61;79]$

Bedeutung beschreiben

Mit einer Wahrscheinlichkeit von etwa $95,5\,\%$ weicht die Anzahl der Treffer von Spieler $M$ in $100$ Versuchen maximal um neun vom Erwartungswert von $70$ ab.

Oder: Mit einer Wahrscheinlichkeit von ca. $95,5\,\%$ beträgt die Anzahl der Treffer von Spieler $M$ in $100$ Versuchen mindestens $61$ und höchstens $79.$

3.2

Mit dem Satz von Bayes kann die Wahrscheinlichkeit $P_{20}(M)$ berechnet werden:

Rechenweg anzeigen

$P_{20}(M)\approx 74,17\,\%$

Mit einer Wahrscheinlichkeit von ca. $74,17\,\%$ handelt es sich bei dem zufällig ausgewählten Spieler, der das Feld „20“ trifft, um Spieler $M.$

3.3.1

Die Zufallsgröße $Z$ beschreibt die Anzahl der Treffer des Feldes „20“ von Spieler $M$ bei $200$ Würfen.

Diese wird als binomialverteilt mit $n=200$ und $p$ entsprechend der Nullhypothese angenommen:

$H_0:\; p=0,7$

Die Alternativhypothese lautet entsprechend:

$H_1:\; p \gt 0,7$

Es soll gelten:

$P(Z\geq k)\leq 0,05$

Rechenweg anzeigen

In der Tabelle für die Binomialsummenfunktion kann nun der entsprechend kleinste Wert für $k-1$ gesucht werden. Dieser folgt mit:

$k-1 \geq 151$

Somit muss gelten: $k \geq 152$

Es kann also folgende Entscheidungsregel definiert werden:

Trifft Spieler $M$ von den $200$ Pfeilen mindestens $152,$ so kann er davon ausgehen, dass das Training erfolgreich war und sich seine Trefferwahrscheinlichkeit erhöht hat. Trifft er weniger als $152$ Pfeile, so kann er nicht von einer verbesserten Trefferquote ausgehen.

3.3.2

Der Fehler zweiter Art wird begangen, wenn die Nullhypothese fälschlicherweise nicht abgelehnt wird, obwohl die Alternativhypothese gilt.

Zu Betrachten ist also wieder die Zufallsgröße $Z$ aus Aufgabe 3.3.1 für $n=200.$ Es wird angenommen, dass diese in Wirklichkeit entsprechend der Alternativhypothese mit $p = 0,78$ binomialverteilt ist.

Der Fehler zweiter Art wird begangen, wenn $Z\leq 151$ ist.

Mit der Tabelle zur Binomialsummenfunktion folgt:

$\begin{array}[t]{rll} P(Z\leq 151)&\approx& 0,2193 \\[5pt] &=& 21,93\,\% \end{array}$

Für den Fall, dass die tatsächliche Trefferwahrscheinlichkeit von Spieler $M$ auf $78\,\%$ gestiegen ist, beträgt die Wahrscheinlichkeit für einen Fehler zweiter Art etwa $21,93\,\%.$