A1 - Analysis

Um im Alltag leistungsfähiger zu sein, greifen inzwischen viele Menschen zu Koffein in unterschiedlichen Verabreichungsformen. Bei einer Studie wurde herausgefunden, dass ein Maß für die Koffeinmenge im Blut in Abhängigkeit von der Zeit nach der Einnahme einer bestimmten Koffeinmenge durch die Funktionenschar

$f_{a,b}(t) = 0,05 \cdot a \cdot \mathrm e^{-\frac{2 \cdot t}{b}}\cdot (t - 20),$ $t \geq 20,$ $a, b \gt 0$

gut modelliert werden kann. Dabei ist $t$ die Zeit in Minuten nach der Einnahme, $a$ ein Maß für die eingenommene Koffeinmenge und $b$ eine Konstante, die aufgrund der Verabreichungsart zugeordnet wird. $f_{a,b}(t)$ ist ein Maß für die Menge des Koffeins im Blut.

In Material 1 ist der Graph der zur eingenommenen Koffeinmenge $a = 60$ und der Verabreichungskonstante $b = 150$ (Einnahme als Tablette) zugehörigen Funktion $f_{60, 150}$ und in Material 2 deren Ableitungsgraph abgebildet.

Material 1

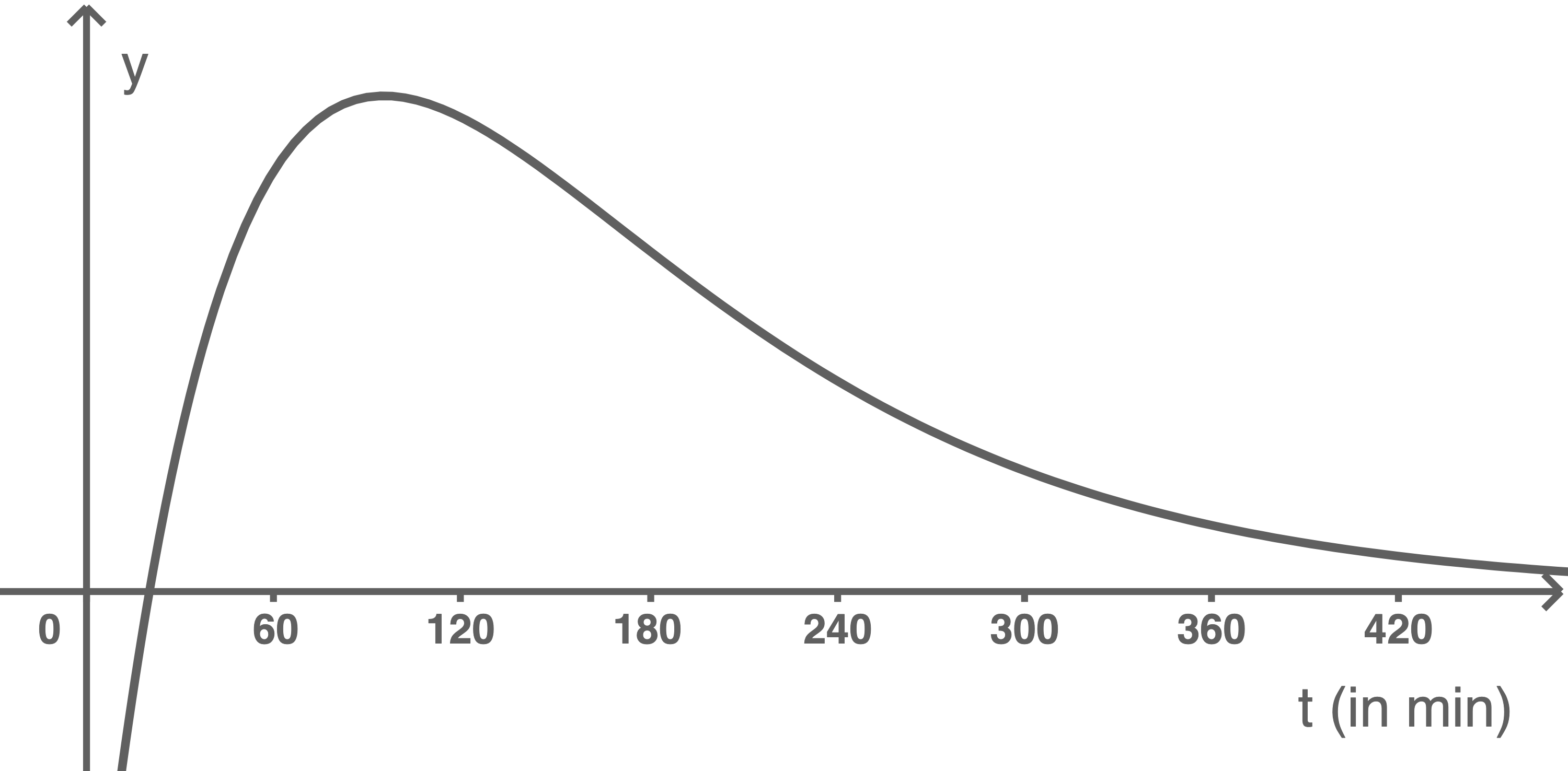
1.1

Begründe durch drei unterschiedliche Argumente, dass der in Material 2 abgebildete Graph die Ableitung der Funktion darstellt, deren Graph in Material 1 gegeben ist.

Material 2

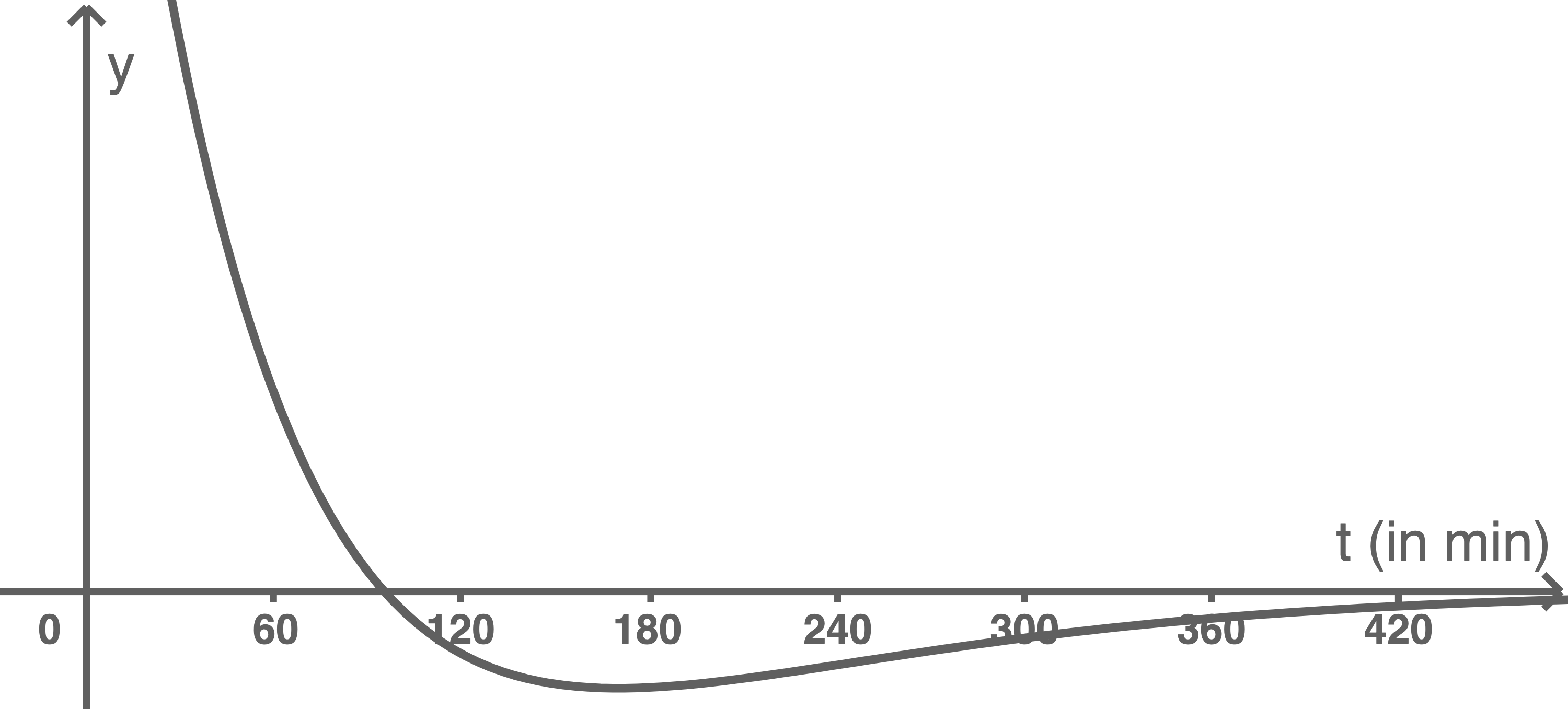
Koffein Funktionenschar Ableitung Hessen Abi 2018

(3 BE)

1.2

Beschreibe den zeitlichen Verlauf der Koffeinmenge im Blut nach der Einnahme des Koffeins.
Begründe, warum die Einschränkung $t \geq 20$ für die Modellierung sinnvoll ist.

(4 BE)

1.3

Berechne den Zeitpunkt der maximalen Koffeinmenge im Blut.
Bestimme den Zeitpunkt, an dem die Abnahme der Koffeinmenge im Blut maximal ist.
Die Überprüfung der notwendigen Bedingung ist jeweils ausreichend.

(8 BE)

2.1

In Material 3 wird die Ermittlung der Stammfunktionen von $f_{60, 150}$ durch eine bestimmte Integrationsmethode angedeutet. Gib die Integrationsmethode an und berechne die Stammfunktionen von $f_{60, 150}.$

Material 3 anzeigen

(5 BE)

2.2

Nachdem Konsumenten der Tabletten vermehrt über Unwohlsein geklagt haben, wurde bei einer weiteren Studie festgestellt, dass der Inhalt der Fläche, die der Graph von $f_{60, 150}$ mit dem Graphen der Funktion $g$ mit $g(t) = 50$ einschließt, ein Maß für die Gesundheitsgefährdung darstellt. Ist dieser Wert größer als $750,$ können bei täglichem Konsum gesundheitliche Schäden auftreten.
Entscheide, ob bei Verabreichung in Tablettenform $(b = 150)$ mit jeweils einer eingenommenen Koffeinmenge von $a = 60$ bei täglichem Konsum gesundheitliche Schäden auftreten können.

(7 BE)

Zeige, dass jeder Graph der Funktionenschar $f_{a,b}$ genau einen Hochpunkt besitzt. Bestimme die Funktionsgleichung der Funktion, auf deren Graph die Hochpunkte aller Graphen der Funktionenschar $f_{a,b}$ liegen (Ortskurve), und begründe damit, dass die Verabreichungsart keinen Einfluss auf den Verlauf der Ortskurve hat.

(7 BE)

Eine Person hat ein Koffeinzäpfchen mit unbekannter Koffeinmenge ausprobiert (Verabreichungskonstante $b = 200$ ). Kurz nach der Einnahme stellen sich gesundheitliche Probleme ein und die Person wird in ein Krankenhaus eingeliefert. Bei vier Blutentnahmen bei der Person wird das Maß für die Koffeinmenge im Blut $y(t)$ jeweils in stündlichen Abständen nach der Einnahme bestimmt und in folgender Tabelle festgehalten:

$t$	$y(t)$
$60$	$100$
$120$	$150$
$180$	$130$
$240$	$100$

Für die weitere Behandlung der Person ist es wichtig, das Maß für die eingenommene Koffeinmenge $a$ so genau wie möglich zu kennen. Dafür bestimmt man das Minimum der Funktion $q$ mit

$q(a) = ...$

Vollständige Lösung anzeigen

Erkläre den Ansatz und bestimme den gesuchten Wert von $a.$

Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.

(6 BE)

1.1

Der Graph in Material 1 besitzt bei $t\approx 90$ einen Hochpunkt. Dies bedeutet, dass die zugehörige Ableitung an dieser Stelle eine Nullstelle mit Vorzeichenwechsel von positiv zu negativ besitzen muss, was der Graph in Material 2 erfüllt.
Der Graph in Material 1 besitzt bei $t\approx 160$ einen Wendepunkt, indem der Graph von einer Rechtskrümmung in eine Linkskrümmung wechselt. Der Graph der zugehörigen Ableitungsfunktion muss an dieser Stelle also einen Tiefpunkt besitzen. Diese Bedingung erfüllt der Graph in Material 2.
Die in Material 1 dargestellte Funktion ist im Bereich von $t\approx 20$ bis zum Hochpunkt streng monoton steigend, der Graph nähert sich anschließend streng monoton fallend der $x$ -Achse als Asymptote an. Da die erste Ableitungsfunktion die Steigung des Graphen beschreibt, muss der zugehörige Ableitungsgraph entsprechend erst oberhalb der $x$ -Achse verlaufen, dann an der Stelle $t\approx 90$ das Vorzeichen wechseln und anschließend unterhalb der $x$ -Achse verlaufen und sich dieser ebenfalls asymptotisch annähern. Dies erfüllt der Graph in Material 2 ebenfalls.

Der in Material 2 abgebildete Graph stellt folglich die Ableitung der Funktion des Graphen aus Material 1 dar.

1.2

Zeitlichen Verlauf beschreiben

$20$ Minuten nach der Einnahme beginnt der Koffeingehalt im Blut extrem schnell zu steigen, bis er ca. $90$ Minuten nach der Einnahme ihr Maximum erreicht hat. Danach nimmt die Koffeinmenge erst relativ schnell ab bis sie etwa $160$ Minuten nach Einnahme den Zeitpunkt erreicht, zu dem sie am schnellsten abnimmt. Anschließend beginnt sie langsamer abzunehmen, nimmt aber immer weiter ab und nähert sich asymptotisch immer weiter dem Wert Null an.

Einschränkung begründen

Im Zeitraum $0\leq t \leq 20,$ also in den ersten zwanzig Minuten nach Einnahme, verläuft der Graph in Material 1 unterhalb der $x$ -Achse, die Koffeinmenge im Blut wäre also negativ. Dies ergibt im Sachzusammenhang keinen Sinn, da es keine negativen Werte geben kann und es auch erst sinnvoll ist den Koffeingehalt zu messen und zu betrachten, wenn eine signifikante Menge im Blut vorhanden ist.

1.3

Zeitpunkt der maximalen Koffeinmenge berechnen

Ableitungsfunktion bilden:

Mit der Produkt- und Kettenregel folgt:

Rechenweg anzeigen

$f_{60,150}(t)= 3 \cdot \mathrm e^{-\frac{t}{75}}\cdot (t-20)$

Rechenweg anzeigen

$\(f_{60,150}$

Notwendiges Kriterium anwenden:

Rechenweg anzeigen

$t=95$

Da laut Aufgabenstellung das notwendige Kriterium genügt, ist also 95 Minuten nach der Einnahme die Koffeinmenge im Blut am höchsten.

Zeitpunkt der maximalen Abnahme bestimmen

Der Zeitpunkt der maximalen Abnahme entspricht im Modell dem Zeitpunkt $t,$ zu dem die erste Ableitungsfunktion $\(f_{60,150}$ ihr Minimum annimmt. Gesucht ist folglich eine Wendestelle von $f_{60,150}.$

Zweite Ableitung bilden:

Rechenweg anzeigen

$\( f_{60,150}$

Notwendiges Kriterium anwenden:

Rechenweg anzeigen

$t=170$

Da laut Aufgabenstellung das notwendige Kriterium genügt, nimmt die Koffeinmenge im Blut $170$ Minuten nach der Einnahme am stärksten ab.

2.1

In Material 2 wird die Methode der partiellen Integration verwendet.

$\displaystyle\int_{}^{}3(t-20)\cdot \mathrm e^{-\frac{1}{75}\cdot t}\;\mathrm dt=...$

Rechenweg anzeigen

Die Stammfunktionen von $f_{60,150}$ sind also:

$F_{60,150,c}(t) = -225\cdot \mathrm e^{-\frac{1}{75}\cdot t}\cdot \left(t+55 \right) +c$

2.2

Der Inhalt der beschriebenen Fläche kann mithilfe eines Integrals bestimmt werden.

Die Integrationsgrenzen entsprechen den Schnittstellen des Graphen von $f_{60,150}(t)$ und des Graphen von $g(t).$

Mit dem CAS folgt:

$\begin{array}[t]{rll} f_{60,150}(t)&=& g(t) \\[5pt] 3 \cdot \mathrm e^{-\frac{t}{75}}\cdot (t-20)&=& 50 &\quad \scriptsize \mid\; CAS \\[5pt] t_1&\approx& 54,4437 \\[5pt] t_2&\approx& 159,173 \end{array}$

Das entsprechende Integral kann mit dem CAS bestimmt werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$\displaystyle\int_{54,4437}^{159,173}\left(f_{60,150}(t)-g(t)\right)\;\mathrm dt=...$

Rechnung anzeigen

Dieser Wert übersteigt deutlich den vorgegebenen Wert von $750.$ Bei täglichem Konsum der Koffeintabletten können also gesundheitliche Schäden auftreten.

Eindeutigkeit der Hochpunkte zeigen

Ableitungsfunktionen bestimmen

$\begin{array}[t]{rll} f_{a,b}(t)&=& 0,05 \cdot a \cdot \mathrm e^{-\frac{2 \cdot t}{b}}\cdot (t - 20) \\[5pt] \end{array}$

$\( f_{a,b}$

Erste Ableitung anzeigen

$\( f_{a,b}$

Zweite Ableitung anzeigen

1. Schritt: Notwendiges Kriterium anwenden

Rechenweg anzeigen

$t=\frac{b}{2} + 20$

Die Graphen von $f_{a,b}$ können also jeweils maximal einen Extrempunkt besitzen.

2. Schritt: Hinreichendes Kriterium überprüfen

Rechenweg anzeigen $\( f_{a,b}$

Wegen $a,b\gt 0$ und $\mathrm e^{-\frac{b+ 40}{b}} \gt 0$ folgt:

$-0,1 \cdot \frac{a}{b}\cdot \mathrm e^{-\frac{b+ 40}{b}}\lt 0$

Die Graphen der Schar $f_{a,b}$ besitzen folglich jeweils genau einen Hochpunkt an der Stelle $t= \frac{b}{2} + 20.$

Ortskurve bestimmen

Die zugehörige $y$ -Koordinate lautet:

$f_{a,b}\left(\frac{b}{2} + 20 \right)=...$

Lösung anzeigen

Durch Umformen der $t$ -Koordinate des Hochpunkts nach $b$ folgt:

$\begin{array}[t]{rll} t&=& \frac{b}{2} + 20 &\quad \scriptsize \mid\; -20\\[5pt] t-20 &=& \frac{b}{2} &\quad \scriptsize \mid\;\cdot 2 \\[5pt] 2t-40 &=& b \end{array}$

Einsetzen in die $y$ -Koordinate ergibt:

Rechenweg anzeigen

$y= (0,05t-1)\cdot a \cdot \mathrm e^{-\frac{t}{t-20}}$

Die Hochpunkte der Graphen der Funktionenschar liegen also alle auf dem Graphen der Funktion mit der Funktionsgleichung:

$y = (0,05t-1)\cdot a \cdot \mathrm e^{-\frac{t}{t-20}}$

Diese Funktionsgleichung ist unabhängig vom Parameter $b,$ der von der Verabreichungsart abhängt. Die Verabreichungsart hat also keinen Einfluss auf die Ortskurve.

Ansatz erklären

In dem Ansatz wird die Methode der kleinsten Quadrate angewendet.

Es wird die Abweichung zwischen den Funktionswerten der Modellfunktion $f_{a,200}$ an den Messstellen zu den tatsächlichen Messwerten betrachtet. Diese Abweichungen können sowohl positiv als auch negativ sein, sodass sich positive und negative Abweichungen gegenseitig in der Summe ausgleichen könnten. Damit dies nicht geschieht werden die einzelnen Abweichungen quadriert.

Um eine möglichst geringe Abweichung der Modellfunktion von den tatsächlichen Messwerten zu erhalten, wird der Parameter $a$ dann so gewählt, dass $q(a)$ minimal ist.

Wert bestimmen

Die Funktionsgleichung von $f_{a,200}$ lautet:

$\begin{array}[t]{rll} f_{a,200}(t) &=& 0,05 \cdot a \cdot \mathrm e^{-\frac{2 \cdot t}{200}}\cdot (t - 20) \\[5pt] &=& 0,05 \cdot a \cdot \mathrm e^{-\frac{ t}{100}}\cdot (t - 20) \end{array}$

Mit dem CAS kann die Funktion $f_{a,200}$ und anschießend die Funktion $q$ definiert werden, indem auf die Funktion $f_{a,200}$ zurückgegriffen wird.

Anschließend kann mit dem CAS die erste Ableitung von $q$ gebildet werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} q$

Der gesuchten Wert folgt also mit $a\approx 97,6894.$