C2 - Stochastik

$70\,\%$ der auf Hühnerfarm $A$ produzierten Eier sind braun, die restlichen weiß. Der Produktion werden nacheinander Eier zufällig ohne Zurücklegen entnommen; es wird jeweils die Farbe notiert.

1.1

Begründe, dass es sich hierbei in guter Näherung um eine Bernoulli-Kette handelt.

(2 BE)

1.2

Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse unter Angabe einer geeigneten Zufallsvariable.

$E_1$ : Unter $10$ der Produktion zufällig entnommenen Eiern sind genau $3$ weiß.
$E_2$ : Unter $50$ der Produktion zufällig entnommenen Eiern sind mindestens $33$ braun.
$E_3$ : Bei $100$ der Produktion zufällig entnommenen Eiern weicht die Anzahl der weißen Eier um höchstens $3$ vom Erwartungswert ab.

(9 BE)

1.3

Die Zufallsvariable $X$ bezeichnet die Anzahl der weißen Eier.
Erläutere den folgenden Ansatz im Sachzusammenhang und berechne $n.$

$P(X\geq 1)=\displaystyle\sum\limits_{k=1}^n \pmatrix{n\\k}\cdot 0,3^k\cdot 0,7^{n-k}\geq 0,99$

(5 BE)

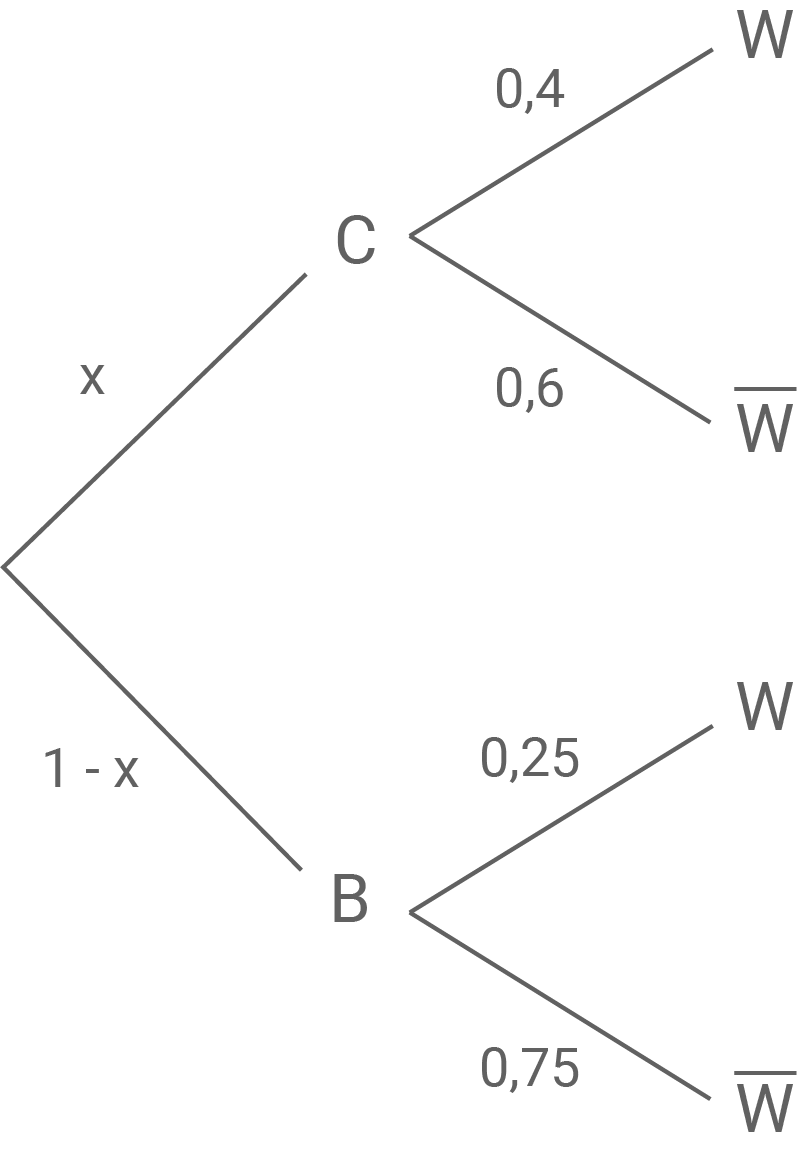
Ein Händler bezieht seine Eier, die entweder braun oder weiß sind, von zwei Hühnerfarmen $B$ und $C.$ Er stellt fest, dass sein Anteil der braunen Eier exakt $70\,\%$ beträgt. Der Anteil der weißen Eier in der Lieferung von Hühnerfarm $C$ beträgt $40\,\%;$ bei Hühnerfarm $B$ beträgt der entsprechende Anteil $25\,\%.$

2.1

Zeige, dass der Händler ein Drittel seiner Eier von Hühnerfarm $C$ bezieht.

(4 BE)

2.2

Ein Ei wird aus dem Lager des Händlers zufällig ausgewählt; es ist weiß. Bestimme die Wahrscheinlichkeit dafür, dass es sich um ein Ei aus der Lieferung von Hühnerfarm $C$ handelt.

(3 BE)

Auf der Hühnerfarm $D$ werden ebenfalls Eier produziert, die entweder braun oder weiß sind. Der Betreiber behauptet, dass der Anteil der weißen Eier in seiner Produktion größer als $30\,\%$ ist. Um seine Vermutung zu bestätigen, untersucht er $200$ Eier.

3.1

Entwickle einen Hypothesentest auf einem Signifikanzniveau von $5\,\%$ und formuliere eine Entscheidungsregel im Sachzusammenhang.

(6 BE)

3.2

Beschreibe den Fehler zweiter Art im Sachzusammenhang und bestimme seine Wahrscheinlichkeit für den Fall, dass der tatsächliche Anteil der weißen Eier $35\,\%$ beträgt.

(5 BE)

3.3

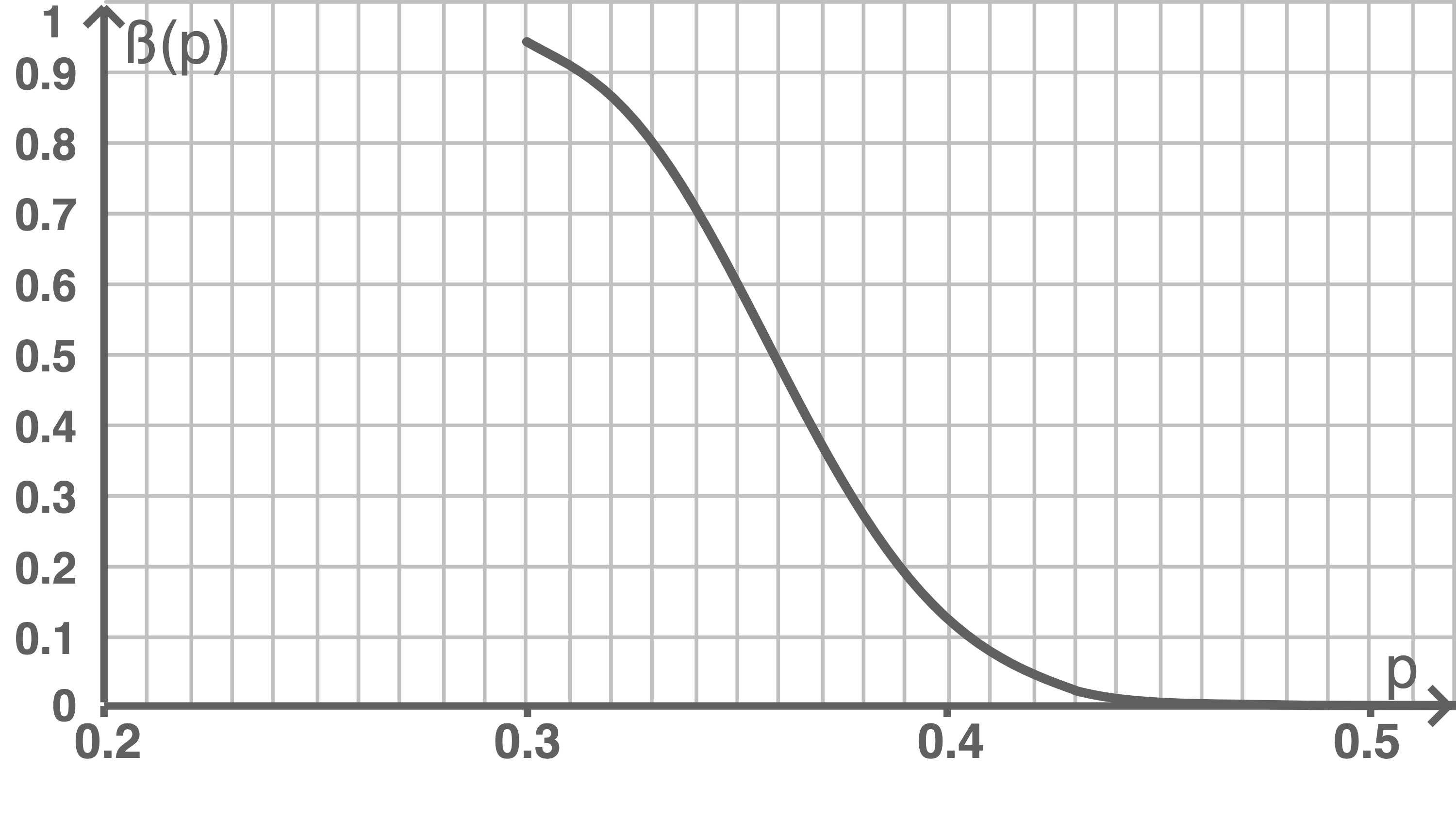
Der Graph im Material zeigt für $n=200$ , wie sich bei einem Signifikanzniveau von $5\,\%$ die Fehlerwahrscheinlichkeit $\beta$ für den Fehler zweiter Art in Abhängigkeit vom tatsächlichen Anteil $p$ weißer Eier mit $p\gt0,3$ verhält.
Beschreibe, wie sich anhand des Graphen das Ergebnis aus Aufgabe 3.2 bestätigen lässt.
Erläutere ohne Verwendung einer Rechnung, wie sich der Verlauf des Graphen für $p\gt0,3$ verändert, wenn das Signifikanzniveau bei $2\,\%$ liegt.

(4 BE)

Auf einem Bauernhof leben freilaufende Hühner. Das Gewicht ihrer Eier sei normalverteilt mit dem Erwartungswert $\mu=57\,g$ und der Standardabweichung $\sigma=4\,g.$ Die Zufallsvariable $X$ gebe das Gewicht eines zufällig herausgegriffenen Eis in Gramm an.

4.1

Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse.
$E_4:$ Das Gewicht eines zufällig ausgewählten Eies liegt zwischen $49\,g$ und $56\,g.$
$E_5:$ Das Gewicht eines zufällig ausgewählten Eies beträgt mindestens $50\,g.$
$E_6:$ Das Gewicht eines zufällig ausgewählten Eies weicht um mindestens $6\,g$ vom Erwartungswert ab.

(7 BE)

4.2

Erläutere den Ansatz $1-\Phi\left(\dfrac{a-57}{4}\right)\leq 0,05$ im Sachzusammenhang und bestimme den kleinsten ganzzahligen Wert für $a$ , für den die Ungleichung erfüllt ist.
Hinweis: $\Phi(1,65)\approx 0,95$ kann verwendet werden.

(5 BE)

Fehlerwahrscheinlichkeit Material Hessen Abi

Binomialsummenfunktion $F_{n;p}(k)=\displaystyle\sum\limits_{i=0}^k\pmatrix{n\\i}\cdot p^i\cdot(1-p)^{n-i}$ für $n=200$

$p=$	$0,3$
$k=$
50	0,0695
51	0,0934
52	0,1228
53	0,1579
54	0,1988
55	0,2455
56	0,2972
57	0,3532
58	0,4123
59	0,4733
60	0,5348
61	0,5953
62	0,6533
63	0,7079
64	0,7579
65	0,8028
66	0,8421
67	0,8758
68	0,9040
69	0,9272
70	0,9458
71	0,9604
72	0,9716
73	0,9800
74	0,9862
75	0,9906
76	0,9938
77	0,9959
78	0,9974
79	0,9984
80	0,9990
81	0,9994
82	0,9996
83	0,9998
84	0,9999
85	0,9999
86	1,0000

Der Wert $1,0000$ bedeutet: Die angegebenen Wahrscheinlichkeiten sind auf vier Stellen gerundet $1,0000$ .

Gaußsche Summenfunktion $\Phi(x)$

	B	C	D	E	F	G	H	I	J	K	L	M
1
2
3
4	x	0	1	2	3	4	5	6	7	8	9	x
5	-3,9	0	0	0	0	0	0	0	0	0	0	-3,9
6	-3,8	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	-3,8
7	-3,7	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	-3,7
8	-3,6	0,0002	0,0002	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	-3,6
9	-3,5	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	-3,5
10	-3,4	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0002	-3,4
11	-3,3	0,0005	0,0005	0,0005	0,0004	0,0004	0,0004	0,0004	0,0004	0,0004	0,0003	-3,3
12	-3,2	0,0007	0,0007	0,0006	0,0006	0,0006	0,0006	0,0006	0,0005	0,0005	0,0005	-3,2
13	-3,1	0,001	0,0009	0,0009	0,0009	0,0008	0,0008	0,0008	0,0008	0,0007	0,0007	-3,1
14	-3	0,0013	0,0013	0,0013	0,0012	0,0012	0,0011	0,0011	0,0011	0,001	0,001	-3
15	-2,9	0,0019	0,0018	0,0018	0,0017	0,0016	0,0016	0,0015	0,0015	0,0014	0,0014	-2,9
16	-2,8	0,0026	0,0025	0,0024	0,0023	0,0023	0,0022	0,0021	0,0021	0,002	0,0019	-2,8
17	-2,7	0,0035	0,0034	0,0033	0,0032	0,0031	0,003	0,0029	0,0028	0,0027	0,0026	-2,7
18	-2,6	0,0047	0,0045	0,0044	0,0043	0,0041	0,004	0,0039	0,0038	0,0037	0,0036	-2,6
19	-2,5	0,0062	0,006	0,0059	0,0057	0,0055	0,0054	0,0052	0,0051	0,0049	0,0048	-2,5
20	-2,4	0,0082	0,008	0,0078	0,0075	0,0073	0,0071	0,0069	0,0068	0,0066	0,0064	-2,4
21	-2,3	0,0107	0,0104	0,0102	0,0099	0,0096	0,0094	0,0091	0,0089	0,0087	0,0084	-2,3
22	-2,2	0,0139	0,0136	0,0132	0,0129	0,0125	0,0122	0,0119	0,0116	0,0113	0,011	-2,2
23	-2,1	0,0179	0,0174	0,017	0,0166	0,0162	0,0158	0,0154	0,015	0,0146	0,0143	-2,1
24	-2	0,0228	0,0222	0,0217	0,0212	0,0207	0,0202	0,0197	0,0192	0,0188	0,0183	-2
25	-1,9	0,0287	0,0281	0,0274	0,0268	0,0262	0,0256	0,025	0,0244	0,0239	0,0233	-1,9
26	-1,8	0,0359	0,0351	0,0344	0,0336	0,0329	0,0322	0,0314	0,0307	0,0301	0,0294	-1,8
27	-1,7	0,0446	0,0436	0,0427	0,0418	0,0409	0,0401	0,0392	0,0384	0,0375	0,0367	-1,7
28	-1,6	0,0548	0,0537	0,0526	0,0516	0,0505	0,0495	0,0485	0,0475	0,0465	0,0455	-1,6
29	-1,5	0,0668	0,0655	0,0643	0,063	0,0618	0,0606	0,0594	0,0582	0,0571	0,0559	-1,5
30	-1,4	0,0808	0,0793	0,0778	0,0764	0,0749	0,0735	0,0721	0,0708	0,0694	0,0681	-1,4
31	-1,3	0,0968	0,0951	0,0934	0,0918	0,0901	0,0885	0,0869	0,0853	0,0838	0,0823	-1,3
32	-1,2	0,1151	0,1131	0,1112	0,1093	0,1075	0,1056	0,1038	0,102	0,1003	0,0985	-1,2
33	-1,1	0,1357	0,1335	0,1314	0,1292	0,1271	0,1251	0,123	0,121	0,119	0,117	-1,1
34	-1	0,1587	0,1562	0,1539	0,1515	0,1492	0,1469	0,1446	0,1423	0,1401	0,1379	-1
35	-0,9	0,1841	0,1814	0,1788	0,1762	0,1736	0,1711	0,1685	0,166	0,1635	0,1611	-0,9
36	-0,8	0,2119	0,209	0,2061	0,2033	0,2005	0,1977	0,1949	0,1922	0,1894	0,1867	-0,8
37	-0,7	0,242	0,2389	0,2358	0,2327	0,2296	0,2266	0,2236	0,2206	0,2177	0,2148	-0,7
38	-0,6	0,2743	0,2709	0,2676	0,2643	0,2611	0,2578	0,2546	0,2514	0,2483	0,2451	-0,6
39	-0,5	0,3085	0,305	0,3015	0,2981	0,2946	0,2912	0,2877	0,2843	0,281	0,2776	-0,5
40	-0,4	0,3446	0,3409	0,3372	0,3336	0,33	0,3264	0,3228	0,3192	0,3156	0,3121	-0,4
41	-0,3	0,3821	0,3783	0,3745	0,3707	0,3669	0,3632	0,3594	0,3557	0,352	0,3483	-0,3
42	-0,2	0,4207	0,4168	0,4129	0,409	0,4052	0,4013	0,3974	0,3936	0,3897	0,3859	-0,2
43	-0,1	0,4602	0,4562	0,4522	0,4483	0,4443	0,4404	0,4364	0,4325	0,4286	0,4247	-0,1
44	0	0,5	0,496	0,492	0,488	0,484	0,4801	0,4761	0,4721	0,4681	0,4641	0
45	0	0,5	0,504	0,508	0,512	0,516	0,5199	0,5239	0,5279	0,5319	0,5359	0
46	0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753	0,1
47	0,2	0,5793	0,5832	0,5871	0,591	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141	0,2
48	0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,648	0,6517	0,3
49	0,4	0,6554	0,6591	0,6628	0,6664	0,67	0,6736	0,6772	0,6808	0,6844	0,6879	0,4
50	0,5	0,6915	0,695	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,719	0,7224	0,5
51	0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549	0,6
52	0,7	0,758	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852	0,7
53	0,8	0,7881	0,791	0,7939	0,7967	0,7995	0,8023	0,8051	0,8078	0,8106	0,8133	0,8
54	0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,834	0,8365	0,8389	0,9
55	1	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621	1
56	1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,877	0,879	0,881	0,883	1,1
57	1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,898	0,8997	0,9015	1,2
58	1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177	1,3
59	1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319	1,4
60	1,5	0,9332	0,9345	0,9357	0,937	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441	1,5
61	1,6	0,9452	0,9463	0,9474	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545	1,6
62	1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9599	0,9608	0,9616	0,9625	0,9633	1,7
63	1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706	1,8
64	1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,975	0,9756	0,9761	0,9767	1,9
65	2	0,9772	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817	2
66	2,1	0,9821	0,9826	0,983	0,9834	0,9838	0,9842	0,9846	0,985	0,9854	0,9857	2,1
67	2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,989	2,2
68	2,3	0,9893	0,9896	0,9898	0,9901	0,9904	0,9906	0,9909	0,9911	0,9913	0,9916	2,3
69	2,4	0,9918	0,992	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936	2,4
70	2,5	0,9938	0,994	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952	2,5
71	2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,996	0,9961	0,9962	0,9963	0,9964	2,6
72	2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,997	0,9971	0,9972	0,9973	0,9974	2,7
73	2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,998	0,9981	2,8
74	2,9	0,9981	0,9982	0,9982	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986	0,9986	2,9
75	3	0,9987	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,999	0,999	3
76	3,1	0,999	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993	3,1
77	3,2	0,9993	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995	3,2
78	3,3	0,9995	0,9995	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997	3,3
79	3,4	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998	3,4
80	3,5	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	3,5
81	3,6	0,9998	0,9998	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	3,6
82	3,7	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	3,7
83	3,8	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	3,8
84	3,9	1	1	1	1	1	1	1	1	1	1	3,9
85	x	0	1	2	3	4	5	6	7	8	9	x

1.1

Entweder ist ein Ei weiß oder braun, demnach gibt es bei jedem Versuch genau zwei mögliche Ergebnisse.
Auf der Hühnerfarm werden viele Eier produziert, weshalb man davon ausgehen kann, dass sich die Wahrscheinlichkeit für eine bestimmte Farbe durch die Entnahme nicht sehr ändert, solange die Anzahl der entnommenen Eier klein ist gegenüber der Gesamtzahl der weißen und braunen Eier. Somit sind die Ereignisse unabhängig voneinander und es handelt sich folglich um eine Bernoulli-Kette.

1.2

Die Zufallsvariable $X$ beschreibt die Anzahl der weißen Eier.

Ereignis 1

$P(E_1)=P(X=3)=B_{10;0,3}(3)\approx 0,2668$

Ereignis 2

$P(E_2)=P(X\leq 17)=F_{50;0,3}(17)\approx 0,7822$

Ereignis 3

Erwartungswert $E(X)=100\cdot 0,3=30$

$\begin{array}[t]{rll} P(E_3)&=& P(27\leq X\leq 33) & \\[5pt] &=& P(X\leq 33)-P(X\leq 26) & \\[5pt] &=& F_{100;0,3}(33)-F_{100;0,3}(26)& \\[5pt] &\approx& 0,5549 \end{array}$

1.3

Mit diesem Ansatz wird berechnet, wie viele Eier man mindestens entnehmen muss, um mit einer Wahrscheinlichkeit von mindestens $99\,\%$ mindestens ein weißes Ei zu erhalten.

Berechnung von $n$ :

$\begin{array}[t]{rll} P(X\geq 1)&=& 1-P(X=0)\geq 0,99 & \\[5pt] P(X=0)&=& 0,7^n\leq 0,01 \end{array}$

Für $n$ folgt:

$n\geq \log_{0,7}(0,01)\approx 12,91$

Also müssen mindestens $13$ Eier entnommen werden.

2.1

Baumdiagramm Stochastik Eier Hessen Abi 2019

$B$ : Ei von Farm $B$
$C$ : Ei von Farm $C$
$W$ : Ei ist weiß

Daraus folgt:

$x=\dfrac{1}{3}$

Rechenweg anzeigen

2.2

$P_W(C)=\dfrac{P(C\cap W)}{P(W)}=\dfrac{\frac{1}{3}\cdot 0,4}{0,3}=\dfrac{4}{9}$

3.1

$H_0:p\leq 0,3$ , $H_1:p\gt 0,3$

Die Zufallsvariable $X$ beschreibt die Anzahl der weißen Eier und ist binomialverteilt mit $n=200.$

Bei dem rechtsseitigen Test soll gelten:

$\begin{array}[t]{rll} P(X\geq k)&\leq& 0,05 & \\[5pt] P(X\leq k-1)&\geq& 0,95 & \\[5pt] F_{200;0,3}(k-1)&\geq& 0,95 \end{array}$

Aus der Tabelle der Binomialsummenfunktion können folgende Werte abgelesen werden:

$F_{200;0,3}(70)\approx 0,9458$
$F_{200;0,3}(71)\approx 0,9604$

Daraus folgt $k-1=71$ und somit $k=72.$

Der Verwerfungsbereich lautet $V={72,...,200}.$

Die Nullhypothese wird genau dann verworfen, wenn der Betreiber der Farm unter $200$ Eiern mindestens $72$ weiße findet. Er geht dann davon aus, dass der Anteil der weißen Eier in seiner Produktion größer als $30\,\%$ ist.

3.2

Fehler zweiter Art beschreiben

Aufgrund der Testergebnisse geht der Betreiber davon aus, dass der Anteil der weißen Eier höchstens $30\,\%$ beträgt, obwohl er in Wirklichkeit größer als $30\,\%$ ist.

Wahrscheinlichkeit bestimmen

$X:$ Anzahl der weißen Eier, $n=200,$ $p=0,35$

$\beta=P(X\leq 71)=F_{200;0,35}(71)\approx 0,5907$

3.3

Die Wahrscheinlichkeit $\beta(0,35)$ kann an der Stelle $p=0,35$ abgelesen werden.
Die kritische Zahl $k$ erhöht sich, wenn das Signifikanzniveau auf $2\,\%$ erniedrigt wird. Der Verwerfungsbereich wird demnach kleiner und damit die Fehlerwahrscheinlichkeit $\beta$ für den Fehler zweiter Art für jede Wahrscheinlichkeit $p\gt 0,3$ größer, da der Annahmebereich größer ist. Der entsprechende Graph verläuft für $p\gt 0,3$ dann oberhalb des abgebildeten Graphen.

4.1

Die Wahrscheinlichkeiten können mit dem WTR berechnet werden.

$\begin{array}[t]{rll} P(E_4)&=& P(49\leq X\leq 56)& \\[5pt] &\approx& 0,3785 \end{array}$

$\begin{array}[t]{rll} P(E_5)&=& P(X\geq 50) & \\[5pt] &\approx& 0,9599 \end{array}$

$\begin{array}[t]{rll} P(E_6)&=& P(X\leq 51)+P(X\geq 63)& \\[5pt] &\approx& 0,0668+0,0668 & \\[5pt] &=& 0,1336 \end{array}$

4.2

Mit diesem Ansatz lässt sich unter Verwendung der standardisierten Normalverteilung derjenige Wert $a$ für das Gewicht eines Eies bestimmen, für den gilt, dass höchstens $5\,\%$ aller Eier mindestens das Gewicht $a$ besitzen:

$1-\Phi\left(\dfrac{a-57}{4}\right)\leq 0,05$
$\Phi\left(\dfrac{a-57}{4}\right)\geq 0,95$

$\Phi(1,65)\approx 0,95$ , demnach gilt $\dfrac{a-57}{4}\approx 1,65$ , also $a\approx 63,6$

$64$ ist der kleinste ganzzahlige Wert, für den die Ungleichung erfüllt wird.