C1 - Analytische Geometrie

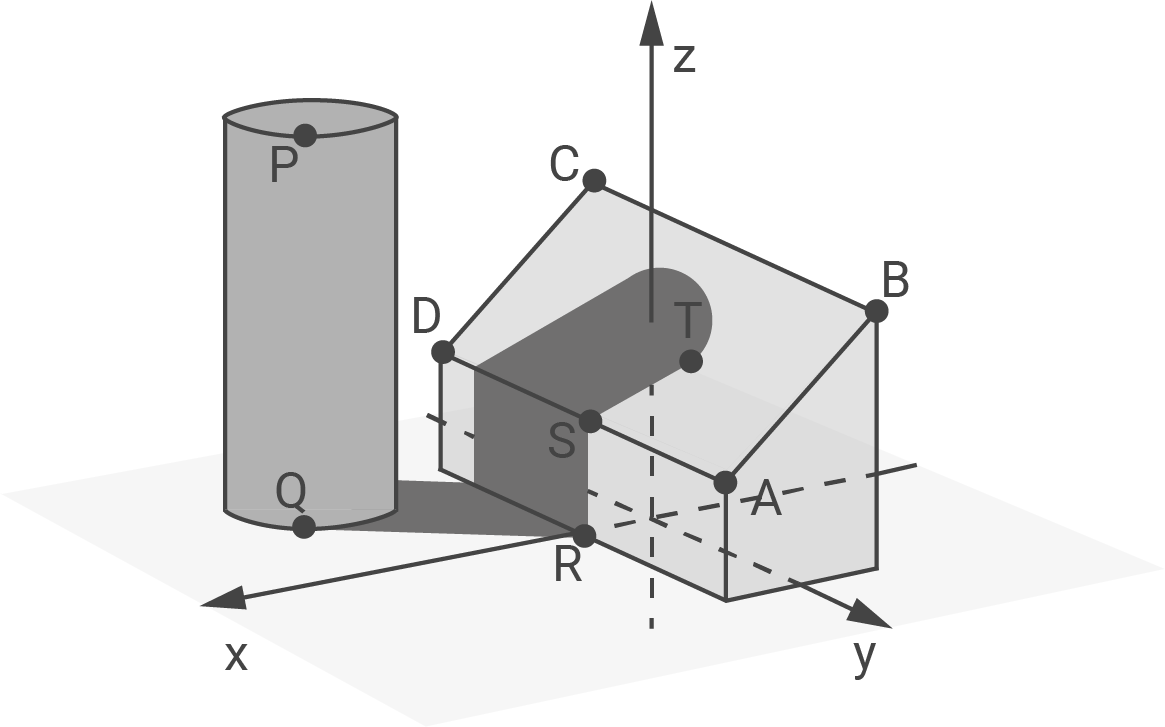
Die Abbildung im Material zeigt modellhaft ein zylinderförmiges Silo, dessen Schatten teilweise auf eine Scheune fällt. Das Silo ist $9,6\,\text{m}$ hoch und hat einen Durchmesser von $4\,\text{m}$ . Die beiden Gebäude stehen senkrecht auf einem horizontalen Untergrund, der im dargestellten kartesischen Koordinatensystem durch die $x$ - $y$ -Ebene beschrieben wird. Eine Längeneinheit im Koordinatensystem entspricht $1\,\text{m}$ in der Realität.
Die Dachfläche der Scheune wird durch das Viereck mit den Eckpunkten $A(2\mid 6\mid 3),$ $B(-2\mid 6\mid 6),$ $C(-2\mid -6\mid 6)$ und $D(2\mid -6\mid 3)$ dargestellt.

1.1

Zeige, dass das Viereck $ABCD$ ein Rechteck ist.
Berechne den Flächeninhalt dieses Rechtecks.

(5 BE)

1.2

Das Viereck $ABCD$ liegt in der Ebene $E$ .
Gib eine Gleichung der Ebene $E$ in Parameterform an und ermittle eine Gleichung von $E$ in Koordinatenform.

[zur Kontrolle: $E:3x+4z=18$ ]

(6 BE)

1.3

In der Koordinatengleichung von $E$ fehlt die $y$ -Koordinate. Beschreibe, was daraus für die Lage der Ebene $E$ im Koordinatensystem folgt.

(2 BE)

1.4

Bestimme die Größe des Winkels, unter dem die Dachfläche der Scheune gegenüber der Horizontalen geneigt ist.

(3 BE)

1.5

Berechne das Volumen und den Flächeninhalt der Oberfläche (ohne Boden) des Silos.

(4 BE)

Die Richtung, in der Sonnenlicht zu einem bestimmten Zeitpunkt auf die beiden Gebäude einfällt, kann durch den Vektor $\pmatrix{-4\\3\\-3}$ beschrieben werden. Der Raumbereich zwischen Silo und Scheune, der vom Sonnenlicht nicht (direkt) erreicht wird, wird von mehreren Flächen begrenzt. Eine dieser Begrenzungsflächen wird durch das ebene Fünfeck $PQRST$ beschrieben, wobei der Punkt $T$ im Modell den Schattenpunkt von $P(7,2\mid -3,4\mid 9,6)$ darstellt (Material).
Die Punkte $Q$ und $R$ liegen jeweils in vertikaler Richtung unterhalb der Punkte $P$ und $S$ auf dem horizontalen Untergrund.

2.1

Das Fünfeck $PQRST$ liegt in der Ebene $F$ . Begründe, dass $F$ durch die Gleichung $3x+4y=8$ beschrieben wird.

(4 BE)

2.2

Berechne die Länge der Strecke $\overline{ST}$ .

(7 BE)

2.3

Begründe, dass die Breite des Schattens des Silos auf der Seitenwand der Scheune nicht genauso groß ist wie der Durchmesser des Silos.

(3 BE)

2.4

Eine zweite Begrenzungsfläche des betrachteten Raumbereichs liegt im Modell in einer Ebene $H:3x+4y=d$ mit $d\in \mathbb{R}$ . Berechne den Wert von $d$ .

(4 BE)

Gegeben ist die Abbildungsmatrix $M$
mit $M=\pmatrix{1&0&-\dfrac{4}{3}\\0&1&1\\0&0&0}$

3.1

Berechne alle Punkte des $\mathbb{R}^3,$ die durch $M$ auf sich selbst abgebildet werden. Beschreibe die Lage dieser Punkte geometrisch.

(4 BE)

3.2

Berechne die Koordinaten aller Punkte des $\mathbb{R}^3,$ die durch $M$ auf den Ursprung abgebildet werden. Beschreibe die Lage dieser Punkte geometrisch.

(5 BE)

3.3

Erkläre, welche geometrische Abbildung mithilfe der Matrix $M$ beschrieben wird.

(3 BE)

Zusatzmaterial

3D-Darstellung eines Zylinders und eines Quaders mit Achsenbeschriftung.

1.1

Rechteck nachweisen

Es muss gezeigt werden, dass $\overrightarrow{AB}=\overrightarrow{DC}$ gilt und $\overrightarrow{AD}$ senkrecht zu $\overrightarrow{AB}$ ist:

$\overrightarrow{AB}=\overrightarrow{DC}=\pmatrix{0\\-12\\0}$

$\overrightarrow{AD}\circ\overrightarrow{AB}=\pmatrix{0\\-12\\0} \circ \pmatrix{-4\\0\\3}=0$

Flächeninhalt berechnen

$\begin{array}[t]{rll} A&=& \left|\overrightarrow{AB}\right|\cdot \left|\overrightarrow{AD}\right| & \\[5pt] &=& \sqrt{4^2 + 3^2} \cdot \sqrt{(-12)^2} & \\[5pt] &=& 5\cdot 12 & \\[5pt] &=& 60 \left[\,\text{m}^2\right] \end{array}$

1.2

Parameterform angeben

$E:\overrightarrow{x}= \overrightarrow{OA}+r\cdot \overrightarrow{AB} +s\cdot \overrightarrow{AD}$

$E:\overrightarrow{x}=\pmatrix{2\\6\\3}+r\cdot\pmatrix{-4\\0\\3}+s\cdot\pmatrix{0\\-12\\0}$

Koordinatenform bestimmen

Aus den beiden Richtungsvektoren kann ein Normalenvektor gebildet werden:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \pmatrix{-4\\0\\3}\times \pmatrix{0\\-12\\0} & \\[5pt] &=& \pmatrix{0\cdot 0- 3\cdot (-12)\\3\cdot 0-(-4)\cdot 0\\(-4)\cdot (-12)-0\cdot 0}& \\[5pt] &=&12\cdot \pmatrix{3\\0\\4} \end{array}$

Einsetzen von $\overrightarrow{n}$ und $A$ in die allgemeine Koordinatengleichung ergibt:

$\begin{array}[t]{rll} E: 3\cdot x+4\cdot z&=& c &\quad \scriptsize \mid\; \text{A Einsetzen} \\[5pt] 3\cdot 2 + 4\cdot 3&=& c & \\[5pt] 18&=& c \end{array}$

Somit ist eine Koordinatenform von $E$ gegeben durch:

$E: 3x+4z=18$

1.3

Die Ebene $E$ verläuft parallel zur $y$ -Achse und somit senkrecht zur $x$ - $z$ -Ebene.

1.4

Normalenvektoren der Ebenen bestimmen:

$\overrightarrow{n_{xy}}=\pmatrix{0\\0\\1}$ , $\overrightarrow{n_{E}}=\pmatrix{3\\0\\4}$

Es gilt:

$\begin{array}[t]{rll} \cos(\varphi)&=&\dfrac{\overrightarrow{n_{xy}}\cdot\overrightarrow{n_{E}}}{\left|\overrightarrow{n_{xy}}\right|\cdot\left|\overrightarrow{n_{E}}\right|} & \\[5pt] \cos(\varphi)&=&\dfrac{\pmatrix{0\\0\\1}\cdot\pmatrix{3\\0\\4}}{\left|\pmatrix{0\\0\\1}\right|\cdot\left|\pmatrix{3\\0\\4}\right|} &\\[5pt] \cos(\varphi)&=& \dfrac{4}{5} &\quad \scriptsize \mid\; \arccos \\[5pt] \varphi&\approx& 37^{\circ} \end{array}$

1.5

Volumen berechnen

$V=(2\,\text{m})^2\cdot\pi\cdot 9,6\,\text{m}\approx 121\,\text{m}^3$

Oberfläche berechnen

$\begin{array}[t]{rll} O&=&\pi\cdot(2\,\text{m})^2+2\cdot\pi\cdot 2\,\text{m}\cdot 9,6\,\text{m} & \\[5pt] & \approx & 133\,\text{m}^2 \end{array}$

2.1

Aus dem Skalarprodukt des Normalenvektors der Ebene $F$ mit dem Richtungsvektor der Sonnenstrahlen folgt, dass die beiden Vektoren orthogonal zueinander sind:

$\pmatrix{3\\4\\0}\circ \pmatrix{-4\\3\\3}=0$

Der Vektor, in dessen Richtung das Sonnenlicht einfällt, ist folglich ein möglicher Spannvektor der Ebene $F$ .

Durch Einsetzen von $P$ in $F$ folgt außerdem, dass $P$ in der Ebene $F$ liegt:

$\; 3\cdot 7,2+4\cdot(-3,4)=8$

Des Weiteren gilt $\pmatrix{3\\4\\0}\cdot\pmatrix{0\\0\\1}=0.$ Also ist die Ebene $F$ parallel zur Symmetrieachse des Zylinders, der das Silo darstellt.

2.2

Koordinaten von $S$ bestimmen

Da der Punkt $S$ die gleiche $x$ - und $z$ -Koordinate wie der Punkt $A$ hat und in der Ebene $F$ liegt, gilt für die $y$ -Koordinate $3\cdot 2+4y=8,$ also $y=0,5$ und somit $S\left(2\mid 0,5\mid 3\right).$

Koordinaten von $T$ bestimmen

Die Gerade $g:\overrightarrow{x}=\pmatrix{7,2\\-3,4\\9,6}+u\cdot\pmatrix{-4\\3\\-3},u\in\mathbb{R}$ verläuft durch die Punkt $P$ und $T$ .

Berechnung des Schnittpunkts $T$ von $g$ und $E:$

$u \approx 1,75$

Rechenweg anzeigen

$\overrightarrow{OT}= \pmatrix{0,2\\1,85\\4,35}$

Rechenweg anzeigen

Länge der Strecke berechnen

$\begin{array}[t]{rll} \left|\overrightarrow{ST}\right|&=&\left|\pmatrix{0,2\\1,85\\4,35}-\pmatrix{2\\0,5\\3}\right| & \\[5pt] &=&\left|\pmatrix{-1,8\\1,35\\1,35}\right| & \\[5pt] &=& \sqrt{1,8^2+1,35^2+1,35^2} & \\[5pt] &\approx& 2,6\,[\,\text{m}] \end{array}$

2.3

Die Breite des Schattens wäre nur dann genauso groß wie der Durchmesser des Silos, wenn das Sonnenlicht parallel zur $x$ - $z$ -Ebene einfallen würde. Allerdings hat der Sonnenlichtvektor $\pmatrix{-4\\3\\-3}$ die $y$ -Koordinate $3,$ dieser Wert müsste $0$ sein um die Bedingung zu erfüllen.

2.4

Gesucht ist die Begrenzungsfläche, die parallel zur Ebene $F$ ist und durch den Punkt $P^*$ verläuft.
$P^*$ ist hierbei der Punkt des Zylinders, der dem Punkt $P$ im Abstand $4$ auf dem oberen Rand des Zylinders gegenüberliegt.

Mit $\left|\overrightarrow{n_H}\right|=\left|\pmatrix{3\\4\\0}\right|=\sqrt{3^2+4^2+0^2}=5$ folgt für den Punkt $P^*$ :

$\begin{array}[t]{rll} \overrightarrow{OP^*}&=&\pmatrix{7,2\\-3,4\\9,6}-4\cdot\dfrac{1}{5}\cdot\pmatrix{3\\4\\0} & \\[5pt] &=&\pmatrix{4,8\\-6,6\\9,6} \end{array}$

Daraus folgt:

$d= 3\cdot 4,8+ 4\cdot (-6,6) =-12$

3.1

Es soll gelten:

$\; \pmatrix{1&0&-\frac{4}{3}\\0&1&1\\0&0&0}\cdot\pmatrix{x\\y\\z}=\pmatrix{x\\y\\z}$

Daraus lässt sich folgendes Gleichungssystem ableiten:

$\begin{array}{lrll} \text{I}\quad&x-\frac{4}{3}z&=&x\quad \scriptsize\\ \text{II}\quad&y+z&=&y &\quad \\ \text{III}\quad&0&=&z &\quad \\ \end{array}$

$\text{III}$ in $\text{II}$ und $\text{I}$ einsetzen ergibt $x=x, \; y=y$ und $z=0.$

Somit werden alle Punkte der Form $\pmatrix{x\\y\\0},$ welche also in der $x$ - $y$ -Ebene liegen, durch $M$ auf sich selbst abgebildet.

3.2

Es soll gelten:

$\pmatrix{1&0&-\frac{4}{3}\\0&1&1\\0&0&0}\cdot\pmatrix{x\\y\\z}=\pmatrix{0\\0\\0}$

Daraus lässt sich folgendes Gleichungssystem ableiten:

$\begin{array}{lrll} \text{I}\quad&x-\frac{4}{3}z&=&0\quad \scriptsize\\ \text{II}\quad&y+z&=&0 &\quad \\ \text{III}\quad&0&=&0 &\quad \\ \end{array}$

$z=t$ in $\text{II}:$ $y=-t$

$z=t$ in $\text{I}:$ $x=\dfrac{4}{3}t$

Es werden folglich alle Punkte der Form $\pmatrix{\frac{4}{3}t\\-1\\1}$ , also alle Punkte auf der Ursprungsgeraden $g:\overrightarrow{x}=t\cdot\pmatrix{\frac{4}{3}\\-1\\1},t\in\mathbb{R}$ , auf den Ursprung abgebildet.

3.3

Es gilt:

Rechnung anzeigen

Also beschreibt die Matrix $M$ eine Projektion eines jeden Punktes des $\mathbb{R}^3$ in die $x$ - $y$ -Ebene.