A - Hilfsmittelfreier Teil
Analysis - Niveau 1
1
Gegeben ist die Funktionenschar 
mit 
und 
1.1
Begründe, dass jeder Graph der Schar einen Tiefpunkt besitzt, und zeige, dass dieser bei
liegt.
(3 BE)
1.2
Bestimme die Funktionsgleichung der Ortskurve der Tiefpunkte.
(2 BE)
Stochastik - Niveau 1
2
Ein Saathändler mischt Tomatensamen zweier verschiedener Qualitätsstufen. 
aller Samen gehören zur höheren Qualitätsstufe. Hiervon keimen nach Angaben des Händlers 
Insgesamt keimen 
der Samen einer Mischung.
Stelle diesen Sachverhalt in einem vollständig beschrifteten Baumdiagramm dar und berechne, wie viel Prozent der Samen der niedrigeren Qualitätsstufe keimen.
Stelle diesen Sachverhalt in einem vollständig beschrifteten Baumdiagramm dar und berechne, wie viel Prozent der Samen der niedrigeren Qualitätsstufe keimen.
(5 BE)
Lineare Algebra/Analytische Geometrie - Niveau 1
3
Gegeben ist das folgende Gleichungssystem:
![\(\begin{vmatrix}
\begin{array}[t]{rll}
4x-4y+8z&=-4&\\[5pt]
-2x-6z&= \;\ 0& \\[5pt]
x-y+2z&=-1& \\[5pt]
\end{array}
\end{vmatrix}\)](https://mathjax.schullv.de/c2c8c1b37e84b4846f701cb959d9cfc78e0b996451a09c80e59e2169eac41865?color=5a5a5a)
3.1
Berechne die Lösungsmenge.
[mögliches Ergebnis: 
]
(4 BE)
3.2
Die drei Gleichungen des Gleichungssystems beschreiben jeweils eine Ebene.
Deute die Lösungsmenge des Gleichungssystems geometrisch.
Deute die Lösungsmenge des Gleichungssystems geometrisch.
(1 BE)
Lineare Algebra/Analytische Geometrie - Niveau 2
4
Gegeben sind die Punkte 
und 
in einem dreidimensionalen Koordinatensystem. Die Punkte 
und 
liegen in einer Ebene und es gilt:
Zeige, dass die Figur 
achsensymmetrisch bezüglich der Achse 
ist.
(5 BE)
1.1
Hinreichende Bedingung für einen Tiefpunkt: 
und 
![\(\begin{array}[t]{rll}
f_k(x) & = & x^2-kx+1 \quad \scriptsize\; \\[5pt]
f_k‘(x)& = & 2x -k \quad \scriptsize\; \\[5pt]
f_k‘‘(x)& = &2 \gt0 &\quad \scriptsize\; \\[5pt]
\end{array}\)](https://mathjax.schullv.de/24358b3111673c7399f8b8783398fc6a199c4d18c5f4f60fe7a8afac36819595?color=5a5a5a)
ist für alle 
größer als 
, sodass jeder Graph der Schar einen Tiefpunkt besitzt.
![\(\begin{array}[t]{rll}
f‘(x)& = &0\quad \scriptsize\; \\[5pt]
2x-k& = &0\quad \scriptsize\; \\[5pt]
2x& = &k\quad \scriptsize\; \\[5pt]
x& = &\dfrac{k}{2}
\end{array}\)](https://mathjax.schullv.de/e523c17d79a25fa944cc20d808109de68f06f5a1751ec375c5cd9b2e233c1517?color=5a5a5a)
in 
einsetzen:
![\(\begin{array}[t]{rll}
f_k\bigg(\dfrac{k}{2}\bigg)& = &\bigg(\dfrac{k}{2}\bigg)^2-k\cdot \bigg(\dfrac{k}{2}\bigg)+1\quad \scriptsize\; \\[5pt]
& = &\dfrac{k^2}{4}-\dfrac{k^2}{2}+1\quad \scriptsize\; \\[5pt]
& = &\dfrac{k^2}{4}-\dfrac{2k^2}{4}+1\quad \scriptsize\; \\[5pt]
& = &-\dfrac{k^2}{4}+1
\end{array}\)](https://mathjax.schullv.de/331381a63cbb9cc1de5c8556c47fbe175d2ee66458484da9287077be0d795348?color=5a5a5a)
Jeder Graph der Schar besitzt somit den Tiefpunkt
Jeder Graph der Schar besitzt somit den Tiefpunkt
1.2
Ortskurve der Tiefpunkte:
-Koordinate nach 
umformen:
![\(\begin{array}[t]{rll}
x&=&\dfrac{k}{2}\quad \scriptsize\; \mid \cdot 2\\[5pt]
k&=&2x
\end{array}\)](https://mathjax.schullv.de/4a357cb0dbcd6c0dc218ff24c5e14dffd842d90774cedd8cbef3fc28758fdb90?color=5a5a5a)
in 
-Koordinate einsetzten:
![\(\begin{array}[t]{rll}
y&=&-\dfrac{k^2}{4}+1\quad \scriptsize\; \\[5pt]
y&=&-\dfrac{(2x)^2}{4}+1\quad \scriptsize\; \\[5pt]
&=&-\dfrac{4x^2}{4}+1\quad \scriptsize\; \\[5pt]
&=&-x^2+1\quad \scriptsize\; \\[5pt]
\end{array}\)](https://mathjax.schullv.de/27344a1c92f9a3467476ed1919ed6528856c971b1a4c3ae0967b5dc3dad29044?color=5a5a5a)
Die Ortskurve aller Tiefpunkte lässt sich durch die Gerade
beschreiben.
Die Ortskurve aller Tiefpunkte lässt sich durch die Gerade
2
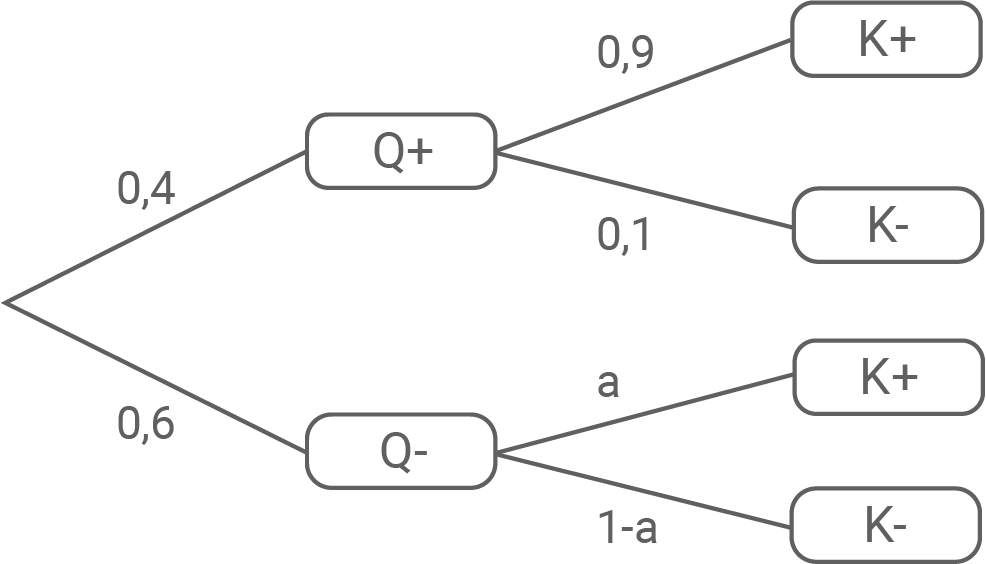
3
Vollständige Lösung anzeigen
3.2
Da die Lösungsmenge einen Parameter besitzt, schneiden sich die Ebenen in einer Geraden.
4
Die Figur ist achsensymetrisch bezüglich der Achse 
wenn gilt:
Die Figur ist achsensymmetrisch bezüglich der Achse , da 
ist.
Die Figur