B1 - Analysis

Gegeben ist die Funktionenschar $f_a$ mit $f_a(t)=a\cdot t\cdot \mathrm e^{-0,25 \cdot t},$ $a\neq 0.$

1.1

Untersuche das Verhalten der Graphen der Schar für $t \rightarrow + \infty.$

(2 BE)

1.2

Ermittle die erste Ableitung der Funktionenschar $f_a$ und zeige, dass für die zweite Ableitung gilt:
$\(f_a(t)$

(6 BE)

1.3

Berechne die Koordinaten des Extrempunktes der Graphen der Funktionenschar $f_a.$
Untersuche in Abhängigkeit vom Parameter $a$ , welche Art von Extrempunkt vorliegt.
[Zur Kontrolle: Die Extremstelle liegt bei $t=4.$ ]

(6 BE)

1.4

Material 1 zeigt einen Graphen der Schar. Bestimme den zugehörigen Wert von $a$ . Zeige, dass die zugehörige Funktionsgleichung auch in der Form $g(t)=t \cdot \mathrm e^{1-0,25 \cdot t}$ dargestellt werden kann.

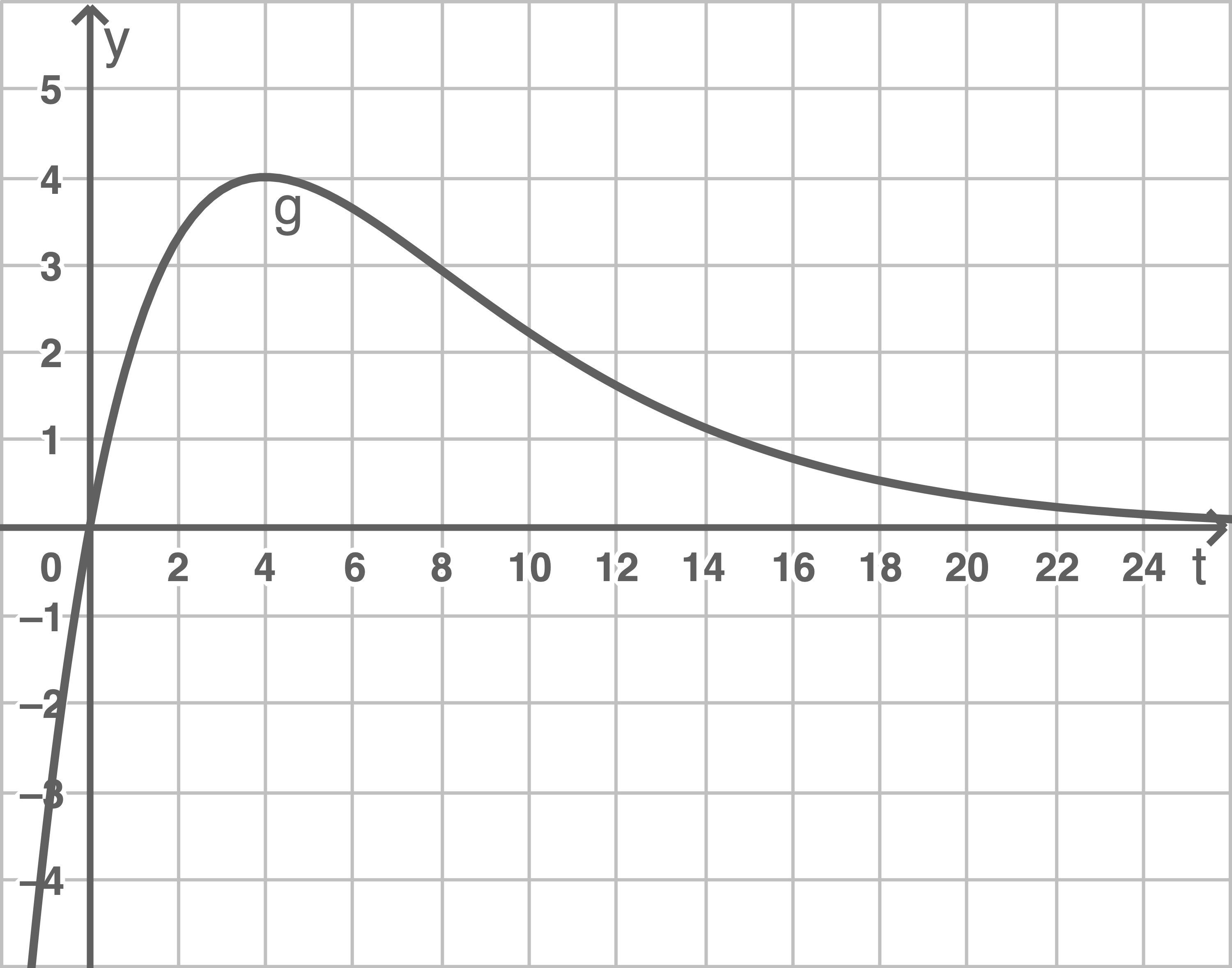
Material 1

(3 BE)

1.5

Beurteile mithilfe von Material 1 die folgende Aussage:
Für $2 \leq t\leq 6$ ändert sich beim Graphen jeder Stammfunktion $G$ von $g$ genau einmal das Krümmungsverhalten.

(2 BE)

1.6

Ermittle mithilfe eines geeigneten Formansatzes eine Stammfunktion $G$ von $g$ .
[Zur Kontrolle: $G(t)=-4\cdot (t+4)\cdot \mathrm e^{1-0,25\cdot t}$ ist die Funktionsgleichung einer möglichen Stammfunktion von $g.$ ]

(5 BE)

1.7

Zeige, dass der Inhalt der Fläche, die der Graph von $g$ im Intervall $t\geq0$ mit der $t$ -Achse einschließt, endlich ist. Ermittle den Inhalt dieser Fläche.

(5 BE)

1.8

Der Inhalt der Fläche, die der Graph der Funktion $g$ mit der $t$ -Achse im Intervall $[2;8]$ einschließt, kann durch zwei unterschiedliche Verfahren näherungsweise bestimmt werden.

$\text{I}.$	Sehnentrapezverfahren mit der Streifenbreite 2 (Material 2)
$\text{II}.$	Kepler'sche Fassregel (Material 3)

Skizziere den Näherungsansatz zum Sehnentrapezverfahren $(\text {I})$ in Material 1.
Ermittle jeweils den Näherungswert (auf drei Nachkommastellen gerundet) und beurteile die Güte der Näherungen durch Vergleich mit dem tatsächlichen Flächeninhalt.

Material 2:
Beim Sehnentrapezverfahren wird der Inhalt einer Fläche, die in einem Intervall vom Graphen der Funktion $g$ und der $t$ -Achse eingeschlossen wird, durch den Flächeninhalt mehrerer trapezförmiger Streifen gleicher Streifenbreite angenähert. Für einen Streifen im Intervall $[a;b]$ gilt: Der Graph von $g$ wird durch eine Sehne zwischen den Punkten $P(a \mid g(a))$ und $Q(b \mid g(b))$ ersetzt. Die Flächeninhalte der jeweils entstehenden Trapeze werden berechnet und addiert.

Material 3:
Die Keplersche Fassregel (nach Johannes Kepler) ist eine Methode zur näherungsweisen Berechnung von Integralen. Zur Berechnung wird folgende Gleichung verwendet:

$\displaystyle\int_{a}^{b}g(t)\;\mathrm dt\approx$ $\dfrac{b-a}{6} \pmatrix{g(a)+4\cdot g \left( \dfrac{a+b}{2} \right)+ g(b)}$

(9 BE)

Ein Patient erhält nach einer Operation ein Medikament per Infusion. Diese ist so eingestellt, dass die Konzentration des Wirkstoffs im Blut in $\,\text{mg}/\ell$ über die Zeit $t$ in Stunden konstant ist. Der Verlauf der Konzentration kann mit der Funktion $h$ mit $h (t)=1$ beschrieben werden. Um die Wirkung des Medikaments zu erhöhen, erhält der Patient das Medikament zusätzlich noch einmal durch eine intravenöse Injektion. Der Verlauf der durch diese Injektion verursachten Konzentration des Wirkstoffs im Blut kann mit der Funktion $g$ mit $g(t)=t\cdot \mathrm{e}^{1-0,25 \cdot t}$ (aus Aufgabe 1.4) beschrieben werden.
Die Funktion $k$ mit $k(t)=1+t \cdot \mathrm{e}^{1-0,25 \cdot t}$ gibt somit für die ersten 24 Stunden ( $t$ in Stunden) den Verlauf der (Gesamt-)Konzentration des Wirkstoffs im Blut in $\,\text{mg}/\ell$ an. Dabei ist $t=0$ der Zeitpunkt, zu dem die intravenöse Injektion des Medikaments erfolgt.

2.1

Zu einem bestimmten Zeitpunkt weist die Änderungsrate der (Gesamt-)Konzentration des Wirkstoffs im Blut ein Extremum auf.
Bestimme diesen Zeitpunkt.
Hinweis: Eine Randwertbetrachtung ist nicht erforderlich.

(3 BE)

2.2

Berechne die durchschnittliche Konzentration, die in den ersten $8 \,\text{h}$ nach Zuführung der zweiten Dosis des Medikaments vorliegt.

(4 BE)

2.3

Die Wirkstoffmenge, die mindestens im Blut vorhanden sein muss, damit das Medikament wirkt, bezeichnet man als therapeutische Konzentration.
Bei dem hier betrachteten Verlauf der Krankheit liegt die therapeutische Konzentration bei $2 \,\text{mg}/\ell.$ Diese muss für einen Zeitraum von mindestens $14 \,\text{h}$ erreicht werden.
Entscheide begründet, ob die vorliegende Medikamentengabe den Bedingungen genügt.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Es gilt $\lim\limits_{t\to +\infty} a\cdot t\cdot \mathrm e^{-0,25t}=0,$ da der lineare Term langsamer gegen unendlich strebt als die Exponentialfunktion gegen Null.

Für $t\rightarrow+\infty$ gilt also $f_a(t)\rightarrow 0.$

1.2

Erste Ableitung ermitteln

Anwendung der Produkt- und Kettenregel:

$\( f_a$

Rechenweg anzeigen

Zweite Ableitung bestimmen

$\( f_a$

Rechenweg anzeigen

1.3

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_a$

Da $a\neq 0$ und $\mathrm e^{-0,25t}\gt 0$ , folgt $1-0,25t=0$ und somit $t=4.$

2. Schritt: Hinreichende Bedingung für Extremstellen prüfen

$\(\begin{array}[t]{rll} f_a$

3. Schritt: $y$ -Koordinate ermitteln

$\begin{array}[t]{rll} f_a(4)&=& a\cdot 4\cdot \mathrm e^{-0,25\cdot 4} & \\[5pt] &=& 4a\cdot \mathrm e^{-1} & \\[5pt] &=&\dfrac{4a}{\mathrm e} \end{array}$

Art des Extrempunkts bestimmen

Für $a \gt 0$ gilt $\(f_a$ und somit haben die Graphen $f_a$ ein Hochpunkt.

Für $a \lt 0$ gilt $\(f_a$ und somit haben die Graphen $f_a$ ein Tiefpunkt.

1.4

Aus dem abgebildeten Graphen lässt sich der Hochpunkt $P(4|4)$ ablesen.

Die $y$ -Koordinate des Hochpunkts wurde in 1.3 bereits abhängig von $a$ berechnet. Durch Einsetzen der $y-$ Koordinate von $P$ folgt:

$\begin{array}[t]{rll} f_a(4)&=&\dfrac{4a}{\mathrm e} & \\[5pt] 4&=&\dfrac{4a}{\mathrm e} & \quad \scriptsize \mid\; \cdot \mathrm e \quad \scriptsize \mid\;:4\\[5pt] \mathrm e&=&a \end{array}$

Die zugehörige Funktion besitzt somit die folgende Gleichung:

$f_\mathrm e(t)=\mathrm e\cdot t\cdot \mathrm e^{-0,25t}.$

Durch Anwendung der Rechenregeln für Exponentialfunktionen ergibt sich:

$\mathrm e\cdot t\cdot \mathrm e^{-0,25t}=t\cdot \mathrm e^1\cdot \mathrm e^{-0,25t}=t\cdot \mathrm e^{1-0,25t}$

1.5

Eine Änderung des Krümmungsverhalten bedeutet, dass der Graph von $G$ einen Wendepunkt in $[2;6]$ besitzt. Die notwendige Bedingung für einen Wendepunkt ist eine Extremstelle in $g$ beziehungsweise eine Nullstelle im Graphen von $\(g$ .

Da $g$ für $2\leq t \leq 6$ seinen einzigen Extrempunkt an der Stelle $t=4$ hat, besitzt auch jede Stammfunktion von $g$ für $2\leq t \leq 6$ genau einen Wendepunkt und ändert folglich genau einmal das Krümmungsverhalten.

Die Aussage ist somit korrekt.

1.6

$g(t)= t\cdot \mathrm e^{1-0,25t}$

Formansatz: $G(t)=(at+b)\cdot \mathrm e^{1-0,25t}$ und $\(G$

Produktregel: $\(G$

Aus $g(t)$ ergeben sich:

$u(t)=at+b$ mit $\(u$

$v(t)=\mathrm e^{1-0,25t}$ mit $\(v$

Eingesetzt in $\(G$ folgt:

Rechenweg anzeigen

$\( G$

Somit gilt: $\; \; \text{I}: -\dfrac{1}{4}a=1 \; \;\; \text{II}: -\dfrac{1}{4}b+a=0$

Aus $\text{I}$ folgt $a=-4$ und aus $\text{II}$ folgt $b=-16.$

Eine Stammfunktion $G$ ist also :

$\begin{array}[t]{rll} G(t)&=&(-4t-16)\cdot \mathrm e^{1-0,25t} & \\[5pt] &=& -4\cdot (t+4)\cdot \mathrm e^{1-0,25t} \end{array}$

1.7

Der Flächeninhalt von $g$ ist genau dann endlich, wenn die Stammfunktion für $t\rightarrow \infty$ einen Grenzwert besitzt:

Rechenweg anzeigen

$\displaystyle\int_{0}^{\infty }g(t)\;\mathrm dt \approx 43,49$

1.8

Skizze Sehnentrapezverfahren

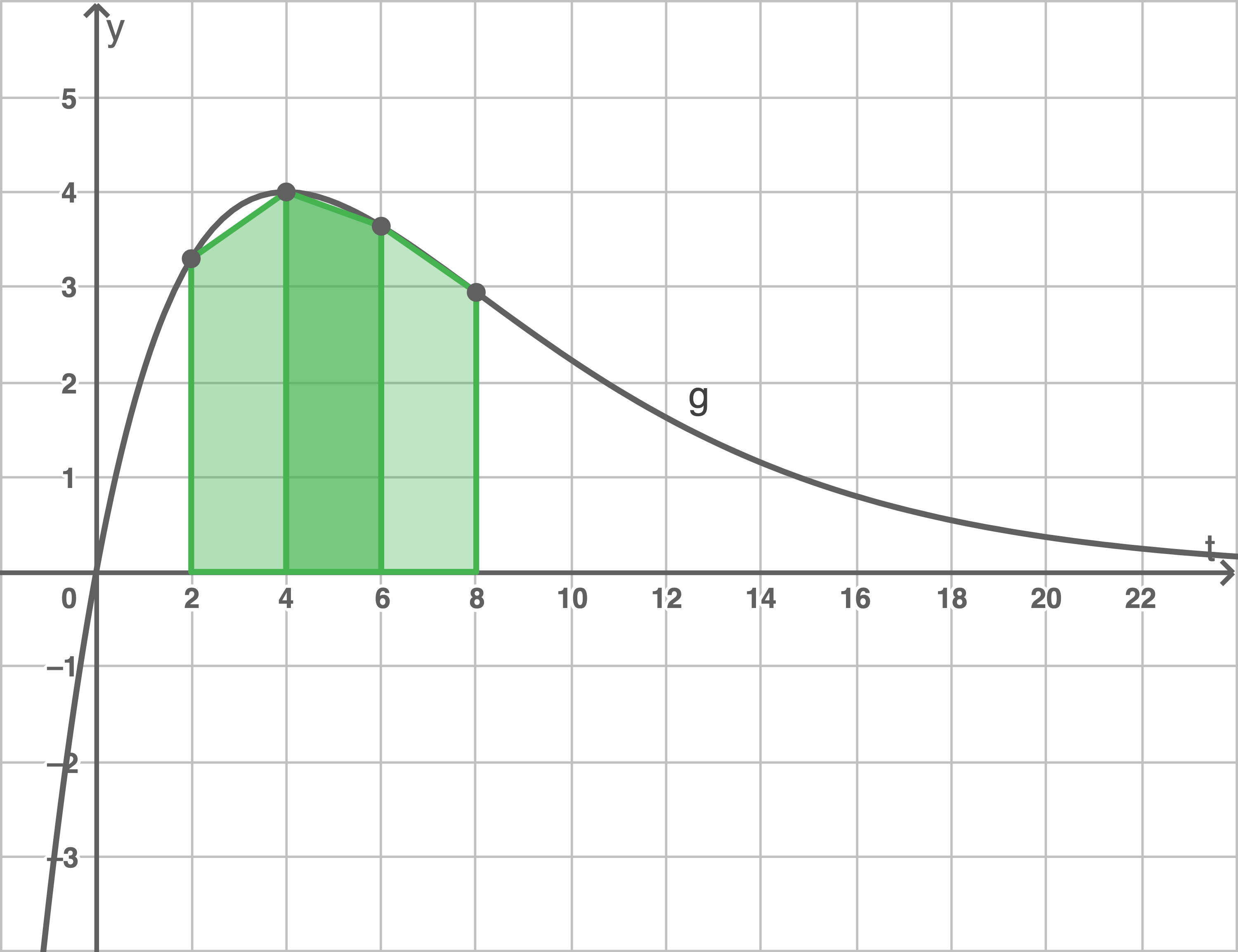Sehnentrapezverfahren Skizze Hessen Abi 2022 Analysis

Näherung Sehnentrapezverfahren

Der Flächeninhalt eines Trapez lässt sich berechnen durch: $A=h\cdot \dfrac{a+c}{2}$

Somit folgt:

$\begin{array}[t]{rll} A_1&=&(4-2)\cdot \dfrac{g(2)+g(4)}{2} & \\[5pt] &=& 2\cdot \dfrac{ 2\cdot \mathrm e^{1-0,25\cdot 2}+ 4\cdot \mathrm e^{1-0,25\cdot 4}}{2} & \\[5pt] &\approx& 7,297 \; [\text{FE}] \end{array}$

$\begin{array}[t]{rll} A_2&=&(6-4)\cdot \dfrac{g(4)+g(6)}{2} & \\[5pt] &=& 2\cdot \dfrac{ 4\cdot \mathrm e^{1-0,25\cdot 4}+ 6\cdot \mathrm e^{1-0,25\cdot 6}}{2} & \\[5pt] &\approx& 7,639 \; [\text{FE}] \end{array}$

$\begin{array}[t]{rll} A_2&=&(8-6)\cdot \dfrac{g(6)+g(8)}{2} & \\[5pt] &=& 2\cdot \dfrac{ 6\cdot \mathrm e^{1-0,25\cdot 6}+ 8\cdot \mathrm e^{1-0,25\cdot 8}}{2} & \\[5pt] &\approx& 6,582 \; [\text{FE}] \end{array}$

Gesamter Flächeninhalt:

$A=A_1+A_2+A_3=21,518 \,\; \text{[FE]}$

Näherung Kepler'sche Fassregel

Rechenweg anzeigen

$\displaystyle\int_{2}^{8}g(t)\;\mathrm dt \approx 21,816 \,\; \text{[FE]}$

Tatsächlicher Flächeninhalt

Rechenweg anzeigen

$\displaystyle\int_{2}^{8}g(t)\;\mathrm dt=21,911$

Die Näherungsansätze durch das Sehnentrapezverfahren und die Kepler'sche Fassregel weichen nur um wenige Dezimalstellen vom tatsächlichen Flächeninhalt ab und sind somit ziemlich genau. Die Kepler'sche Fassregel ist hierbei jedoch genauer als das Sehnentrapezverfahren mit der Streifenbreite 2.

2.1

Das Extremum der Änderungsrate entspricht der Wendestelle von $k.$

1. Schritt: Erste und zweite Ableitung bestimmen

$\(\begin{array}[t]{rll} k$

Rechenweg anzeigen

$\( k$

2. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} k$

Da $\mathrm e^{1-0,25t}\gt 0$ ist, folgt:

$\begin{array}[t]{rll} -\dfrac{1}{2}+\dfrac{t}{16}&=&0 &\quad \scriptsize \mid\; +\dfrac{1}{2} \\[5pt] \dfrac{t}{16}&=&\dfrac{1}{2} &\quad \scriptsize \mid\; \cdot 16 \\[5pt] t&=& 8 \end{array}$

Da gegeben ist, dass ein Extremum der Änderungsrate existiert, ist der Nachweis der hinreichenden Bedingung für Wendestellen nicht mehr nötig.

Folglich weist die Änderungsrate der (Gesamt-)Konzentration des Wirkstoffs im Blut nach 8 Stunden ein Extremum auf.

2.2

Rechenweg anzeigen

$\dfrac{1}{8}\cdot \displaystyle\int_{0}^{8}k(t)\;\mathrm dt \approx 4,229 \;\,\text{[mg/l]}$

In den ersten 8 Stunden nach Zuführung des zweiten Medikaments liegt somit eine durchschnittliche Konzentration von etwa $4,229 \;\,\text{[mg/l]}$ vor.

2.3

Ermitteln des Zeitpunkts, zu welchem die (Gesamt-)Konzentration des Wirkstoffs im Blut den Wert von 2 erreicht und wieder unter diesen Wert fällt:

$\begin{array}[t]{rll} k(t)&=& 2 & \\[5pt] 1+t\cdot \mathrm e^{1-0,25t}&=& 2 \end{array}$

Mit dem solve-Befehl des WTR folgt:

$t_1=0,41$ und $t_2=14,77$

Der Zeitraum, in dem die Konzentration also über $2 \;\,\text{[mg/l]}$ liegt, beträgt:

$14,77-0,41=14,34 \; [\,\text{h}]$

Da eine Konzentration von mehr als $2 \;\,\text{[mg/l]}$ über einen Zeitraum von mehr als 14 Stunden erreicht wird, genügt die vorliegende Medikamentengabe den Bedingungen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?