B2 - Analysis

Gegeben ist die Funktionenschar $f_k$ mit $f_k(t)=k\cdot t\cdot\mathrm e^{-0,4\cdot t},\,$ $k, t \in \mathbb{R}, k\gt0.$

1.1

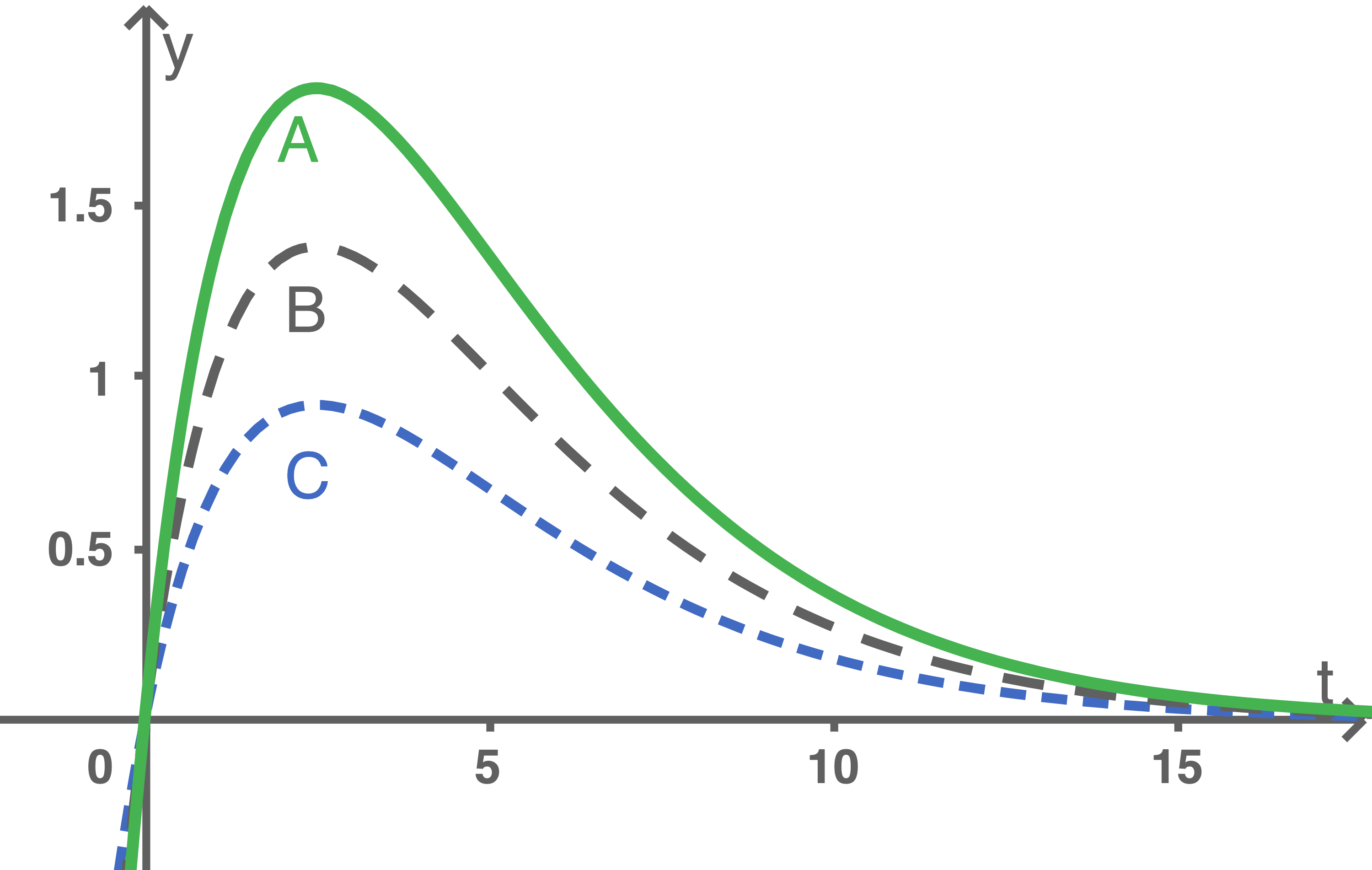
In Material 1 sind die Graphen von $f_1,$ $f_{1,5}$ und $f_2$ dargestellt. Ordne die Graphen $A,$ $B$ und $C$ den verschiedenen Werten des Parameters $k$ zu und begründe deine Zuordnung anhand des Funktionsterms.

Untersuche das Verhalten der Funktionswerte von $f_k$ für $t\rightarrow\infty.$

(4 BE)

1.2

Zeige rechnerisch, dass der Graph jeder Funktion der Schar $f_k$ genau einen Hochpunkt bei $H\left(2,5\mid 2,5\cdot k\cdot \mathrm e^{-1}\right)$ hat.

Beschreibe die Lage der Hochpunkte der Schar.

(9 BE)

1.3

Mithilfe des Formansatzes $F_k(t)=k\cdot\left(a\cdot t+b\right)\cdot \mathrm e^{-0,4\cdot t}$ soll eine Stammfunktionenschar $F_k$ von $f_k$ bestimmt werden.

Berechne die Ableitungsfunktionenschar $\(F$ der Funktionenschar $F_k.$

Ermittle durch Vergleich der Funktionsterme von $\(F$ und $f_k$ eine Stammfunktionenschar $F_k$ von $f_k.$
[zur Kontrolle: $F_k(t)=k\cdot\left(-2,5t-6,25\right)\cdot\mathrm e^{-0,4t}$ ]

(6 BE)

1.4

Untersuche, ob der Graph von $f_k$ mit der positiven $t$ -Achse eine Fläche mit endlichem Inhalt einschließt und berechne ggf. den Flächeninhalt.

(4 BE)

Gegeben ist eine zweite Funktionenschar $g_k$ mit $g_k(t)=k^2\cdot t\cdot\mathrm e^{-0,6t},\,$ $k,t\in\mathbb{R},k\gt0.$

Zeige rechnerisch, dass sich die Graphen der Scharen $f_k$ aus Aufgabe 1 und $g_k$ in den Punkten $S_1(0\mid 0)$ und $S_2\left(\dfrac{\ln k}{0,2}\,\bigg \vert \,\dfrac{\ln k}{0,2\cdot k}\right)$ schneiden und bestimme die Funktionsgleichung der Ortskurve der Schnittpunkte $S_2.$
[zur Kontrolle: $o(t)=t\cdot \mathrm e^{-0,2\cdot t}$ ]

(10 BE)

Mit Nebelfängern (Material 2) lassen sich trockene Gebiete mit Trinkwasser versorgen. Der Nebel kondensiert an Folien, das Wasser sammelt sich und rinnt in Zisternen.
Die Sammelrate eines Nebelfängers vom Typ $I$ kann durch geeignete Funktionen der Schar $f_k$ aus Aufgabe 1, die Sammelrate eines Nebelfängers vom Typ $II$ durch geeignete Funktionen der Schar $g_k$ aus Aufgabe 2 modelliert werden.
Dabei gibt $t$ mit $t\in [0;10]$ die nach 19 Uhr vergangene Zeit in Stunden an; $f_k(t)$ bzw. $g_k(t)$ gibt die Sammelrate des jeweiligen Nebelfängers in hundert Liter pro Stunde an. Die Sammelrate des jeweiligen Nebelfängers hängt von unterschiedlichen Wetterlagen ab, welche mithilfe des Parameters $k$ mit $k\in[1;3]$ modelliert werden können.
Unter der Ausbeute eines Nebelfängers versteht man die in der Zeit von 19 Uhr abends bis 5 Uhr morgens gesammelte Wassermenge.

3.1

Zeige, dass die Ausbeute eines Nebelfängers vom Typ $I$ in hundert Liter in Abhängigkeit von $k$ durch die Funktion $A(k)=5,678\cdot k$ näherungsweise beschrieben wird.

Bestimme die minimal und die maximal mögliche Ausbeute eines Nebelfängers vom Typ $I$ in Liter.

(4 BE)

3.2

Zeige, dass bei der durch den Wert $k=2,08$ modellierten Wetterlage beide Nebelfänger auf ganze Liter gerundet die gleiche Ausbeute erzielen.

(3 BE)

3.3

Erläutere die Zeilen $(I)$ und $(II)$ sowie die Rechensätze in Zeile $(III)$ des Kastens.
Deute die beiden Ergebnisse in Zeile $(III)$ im Sachzusammenhang.

$(I)$ $f_{2,08}(t)=g_{2,08}(t)\Rightarrow t_1=0\;\lor\;t_2\approx 3,66$

$(II)$ $u(t)=f_{2,08}(t)-g_{2,08}(t)$

$(III)$ $\displaystyle\int_{0}^{3,66}u(t)\;\mathrm dt \approx-2,15\;;\;\displaystyle\int_{3,66}^{10}u(t)\;\mathrm dt\approx+2,15$

(5 BE)

Zu jeder durch den Parameter $k$ modellierten Wetterlage gibt es einen Zeitpunkt $t^*\gt0,$ zu dem die Nebelfänger vom Typ $I$ und $II$ die gleiche Sammelrate haben.

4.1

Erkläre, wie man unter Zuhilfenahme des Kontrollergebnisses aus Aufgabe 2 den Zeitpunkt $t^*_{\text{max}}$ berechnen kann, bei dem die beiden Nebelfänger die größtmögliche gleiche Sammelrate haben.

Hinweis: Eine rechnerische Herleitung des Zeitpunktes $t^*_{\text{max}}$ ist nicht erforderlich.

(2 BE)

4.2

Es ergibt sich $t^*_{\text{max}}=5.$ Berechne den zugehörigen Wert des Parameters $k$ .

(3 BE)

Grafik mit drei Kurven A, B und C, die verschiedene Funktionen in einem Koordinatensystem darstellen.

Material 1

Material 2

Bildnachweise [nach oben]

[1]

https://de.wikipedia.org/wiki/Datei:Atrapanieblas_en_Alto_Patache.jpg - Atrapanieblas en Alto Patache, Nicole Saffie, CC BY-SA.

1.1

Graphen zuordnen

Der Parameter $k$ strecht den Graphen für $k\gt 1$ in $y$ -Richtung. Umso größer also $k$ , desto höher liegt der Hochpunkt.

Folglich gehört der Graph $C$ zu $f_1$ , der Graph $B$ zu $f_{1,5}$ und der Graph $A$ zu $f_2.$

Verhalten für $t\rightarrow\infty$ untersuchen

Es gilt $\lim\limits_{t\to\infty}\mathrm e^{-0,4t}=0.$

Da die $\mathrm e-$ Funktion im Term dominiert, folgt somit auch $\lim\limits_{t\to\infty}f_k(t)=0.$

1.2

Erste Ableitung von $\(f_k$ bilden:

Rechenweg anzeigen

$\( f_k$

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_k$

Wegen $k \gt 0$ und $\mathrm e^{0,4t} \gt 0$ folgt mit dem Satz vom Nullprodukt:

Rechenweg anzeigen

$t= 2,5$

2. Schritt: Hinreichende Bedingung für Extremstellen prüfen

$\( f_k$

Rechenweg anzeigen

Wegen $k \gt 0$ gilt $\(f_k$

Somit besitzen die Graphen der Schar an der Stelle $x=2,5$ einen Hochpunkt.

3. Schritt: $y$ -Koordinate bestimmen

$f_k(2,5)=2,5\cdot k\cdot \mathrm e^{-1}$

Die Hochpunkte besitzen folglich die Koordinaten $H\left(2,5\mid 2,5\cdot k\cdot\mathrm e^{-1}\right)$ und liegen somit alle auf einer Parallelen zur $y$ -Achse mit der Gleichung $t=2,5.$

1.3

Ableitungsfunktionenschar $\(F_k$ berechnen

Rechenweg anzeigen

$\( F_k$

Stammfunktionenschar $F_k(t)$ ermitteln

Gesucht sind die Werte der Parameter $a$ und $b$ , für die gilt:

$k\cdot(a-0,4at-0,4b)\cdot\mathrm e^{-0,4t}=k\cdot t\cdot \mathrm e^{-0,4t}$

Durch Koeffizientenvergleich ergibt sich:

$\begin{array}[t]{rll} -0,4a&=& 1 &\\ a-0,4b&=& 0 \end{array}$

Daraus folgen $a=-2,5$ und $b=-6,25$ .

Durch Einsetzen der Werte für $a$ und $b$ in den Formansatz ergibt sich eine Stammfunktionenschar $F_k(t)$ mit $F_k(t)=k\cdot(-2,5t-6,25)\cdot\mathrm e^{-0,4t}$ .

1.4

$\begin{array}[t]{rll} \lim\limits_{v\to\infty}\displaystyle\int_{0}^{v}f_k(t)\;\mathrm dt&=&\lim\limits_{v\to\infty}F_k(v)-F_k(0)&\\ &=&0-(-6,25\cdot k)\\ &=&6,25\cdot k \end{array}$

Dabei gilt:

Folglich schließt der Graph von $f_k$ mit der positiven $t$ -Achse eine Fläche mit dem endlichen Inhalt $6,25\cdot k$ ein.

Schnittpunkte bestimmen

$f_k(t)= g_k(t)$

Rechnung anzeigen

Mit dem Satz vom Nullprodukt folgt:

$t_1=0$ und $\left(\mathrm e^{-0,4t_2}-k\cdot \mathrm e^{-0,6t_2}\right)=0$

Durch Ausklammern ergibt sich:

$t_2 =\dfrac{\ln k}{0,2}$

Rechenweg anzeigen

$y$ -Koordinaten berechnen:

$f_k(0)=0$

$\begin{array}[t]{rll} f_k\left(\dfrac{\ln k}{0,2}\right)&=&k\cdot\dfrac{\ln k}{0,2}\mathrm e^{-0,4\cdot\frac{\ln k}{0,2}}& \\ &=&k\cdot\dfrac{\ln k}{0,2}\cdot\mathrm e^{-2\ln k}&\\ &=&k\cdot\dfrac{\ln k}{0,2}\cdot\left(\mathrm e^{\ln k}\right)^{-2}&\\ &=&k\cdot\dfrac{\ln k}{0,2\cdot k^2}&\\ &=&\dfrac{\ln k}{0,2\cdot k}& \end{array}$

Somit besitzen die Schnittpunkte der beiden Graphen die Koordinaten $S_1(0\mid 0)$ und $S_2\left(\dfrac{\ln k}{0,2}\mid\dfrac{\ln k}{0,2\cdot k}\right).$

Ortskurve bestimmen

$x$ -Koordinate nach $k$ umstellen:

$\begin{array}[t]{rll} t&=& \dfrac{\ln k}{0,2}&\quad \scriptsize \mid\; \cdot 0,2 \\[5pt] 0,2t&=& \ln k&\quad \scriptsize \mid\; \mathrm e^{()} \\[5pt] \mathrm e^{0,2t}&=& k \end{array}$

$k$ in die $y$ -Koordinate einsetzen:

$\begin{array}[t]{rll} y&=&\dfrac{\ln k}{0,2\cdot k} &\\ &=&\dfrac{\ln\mathrm e^{0,2t}}{0,2\cdot\mathrm e^{0,2t}}\\ &=&\dfrac{0,2t}{0,2\cdot\mathrm e^{0,2t}}\\ &=&t\cdot\mathrm e^{-0,2t}\end{array}$

Somit folgt die Funktionsgleichung der Ortskurve mit $o(t)=t\cdot\mathrm e^{-0,2t}.$

3.1

$\begin{array}[t]{rll} A(k)&=&\displaystyle\int_{0}^{10}f_k(t)\;\mathrm dt &\\ &=&\left[F_k(t)\right]_0^{10}\\ &=&k\cdot\left(\left(-31,25\right)\cdot\mathrm e^{-4}+6,25\right)\\ &\approx&5,678\cdot k \end{array}$

$A(1)\approx 5,678$ : Die minimale Ausbeute beträgt etwa $568$ Liter.

$A(3)\approx 17,03$ : Die maximale Ausbeute beträgt etwa $1703$ Liter.

3.2

Mit dem WTR ergibt sich:

$\displaystyle\int_{0}^{10}f_{2,08}(t)\;\mathrm dt\approx 11,80948$

$\displaystyle\int_{0}^{10}g_{2,08}(t)\;\mathrm dt\approx 11,80925$

Beide Nebelfänger erzielen also eine Ausbeute von etwa $1181$ Liter.

3.3

Zeile $I$

Die Funktionsterme der Scharen $f$ und $g$ werden für $k=2,08$ gleichgesetzt, also die Schnittstellen $t_1$ und $t_2$ berechnet.

Zeile $II$

Es wird die Differenzfunktion der beiden Scharen mit $k=2,08$ gebildet. Die Funktion $u(t)$ gibt somit die momentane Differenz der Sammelrate an.

Zeile $III$

Es wird jeweils der Wert des Integrals der Differenzfunktion zwischen den Schnittpunkten im Intervall $[0;10]$ , also zwischen $t_1=0$ und $t_2$ und anschließend zwischen $t_2$ und $t=10$ , bestimmt.

Deutung der Ergebnisse im Sachzusammmenhang:

Der Nebelfänger vom Typ II liefert in den ersten $3,66$ Stunden nach $19$ Uhr $215$ Liter mehr Wasser als der Nebelfänger vom Typ I. Anschließend liefert bis $5$ Uhr morgens der Nebelfänger vom Typ I $215$ Liter mehr Wasser als der vom Typ II.

4.1

Die beiden Nebelfänger haben die gleiche Sammelrate in den Punkten, die die Schnittpunkte der Graphen von $f_k$ und $g_k$ bilden. Diese Schnittpunkte liegen auf dem Graphen der Ortskurve $o$ aus Aufgabe 2, da $t^*>0$ gilt. Um die größtmögliche gleiche Sammelrate zu berechnen, müsste man den Graphen der Ortskurve o auf Hochpunkte untersuchen.

Die $x$ -Koordinate des Hochpunkts des Graphen von $o$ entspricht dem Zeitpunkt $t_{\max }^*$ .

4.2

$\begin{array}[t]{rll} t^*_{max}&=& 5 &\\[5pt] \dfrac{\ln k_{max}}{0,2}&=& 5 &\quad \scriptsize \mid\; \cdot 0,2 \quad \scriptsize \mid\; \mathrm e^{()} \\[5pt] k_{max}&=& \mathrm e^{5\cdot 0,2} &\\[5pt] k_{max}&\approx& 2,72 \end{array}$