A1 - Analysis
1
In einem Nationalpark soll eine neue Tierart angesiedelt werden. Dafür werden zum Zeitpunkt  Tiere ausgewildert, von denen einige bereits trächtig sind. Die mögliche Entwicklung der Geburtenrate dieser Tiere kann durch geeignete Funktionen der drei Funktionsscharen
Tiere ausgewildert, von denen einige bereits trächtig sind. Die mögliche Entwicklung der Geburtenrate dieser Tiere kann durch geeignete Funktionen der drei Funktionsscharen 
 und
und  modelliert werden. Dabei gibt
modelliert werden. Dabei gibt 
 und
und  jeweils die Geburtenrate in Tiere/Jahr in Abhängigkeit von der Zeit
jeweils die Geburtenrate in Tiere/Jahr in Abhängigkeit von der Zeit  in Jahren nach der Auswilderung an. Es gilt
in Jahren nach der Auswilderung an. Es gilt  sowie
sowie  Modell A:
Modell A:  Modell B:
Modell B:  Modell C:
Modell C:  In den Abbildungen 1 bis 3 in Material 1 sind jeweils einige Graphen der Funktionsscharen
In den Abbildungen 1 bis 3 in Material 1 sind jeweils einige Graphen der Funktionsscharen 
 und
und  dargestellt.
Material 1
dargestellt.
Material 1
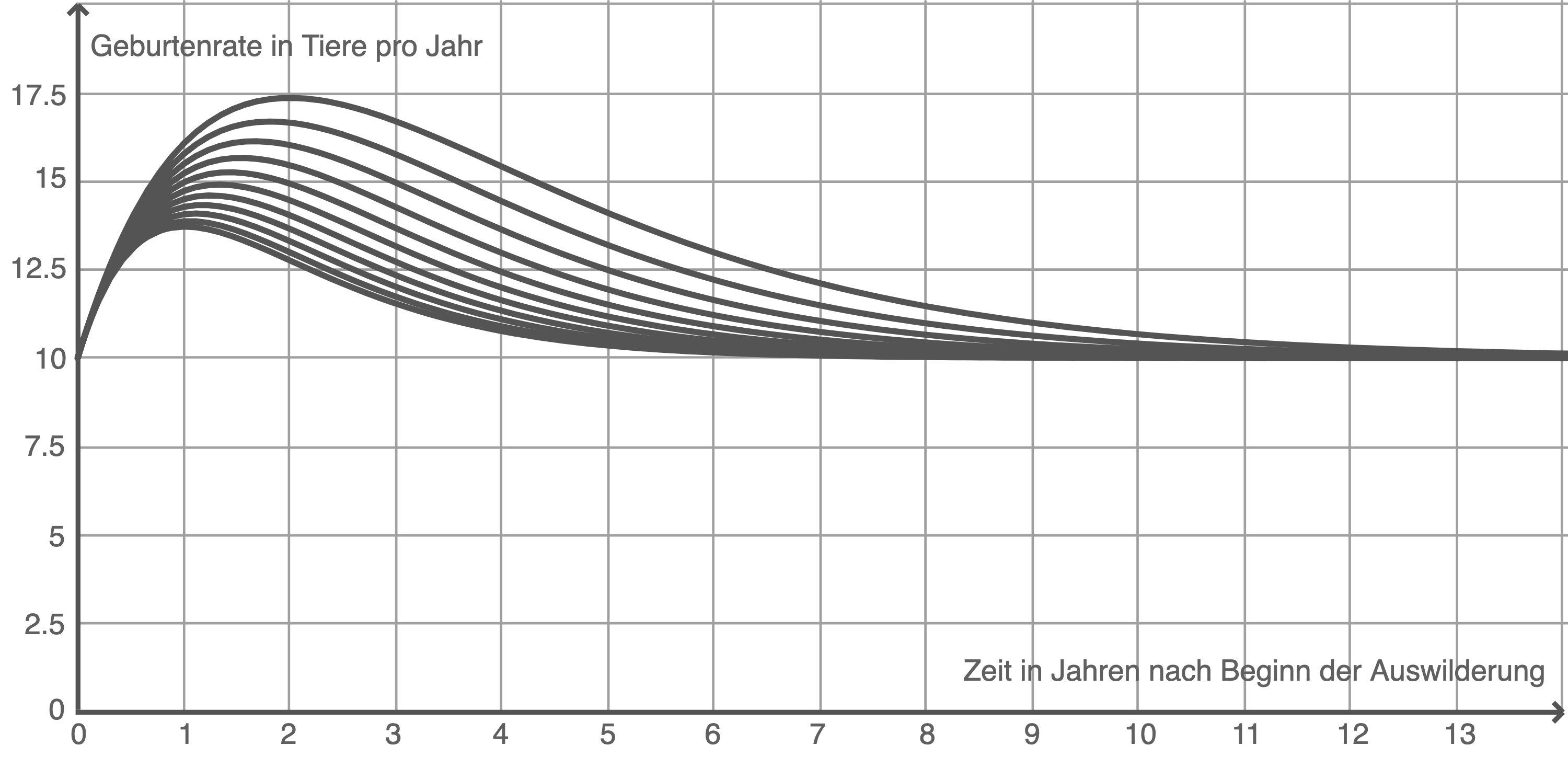
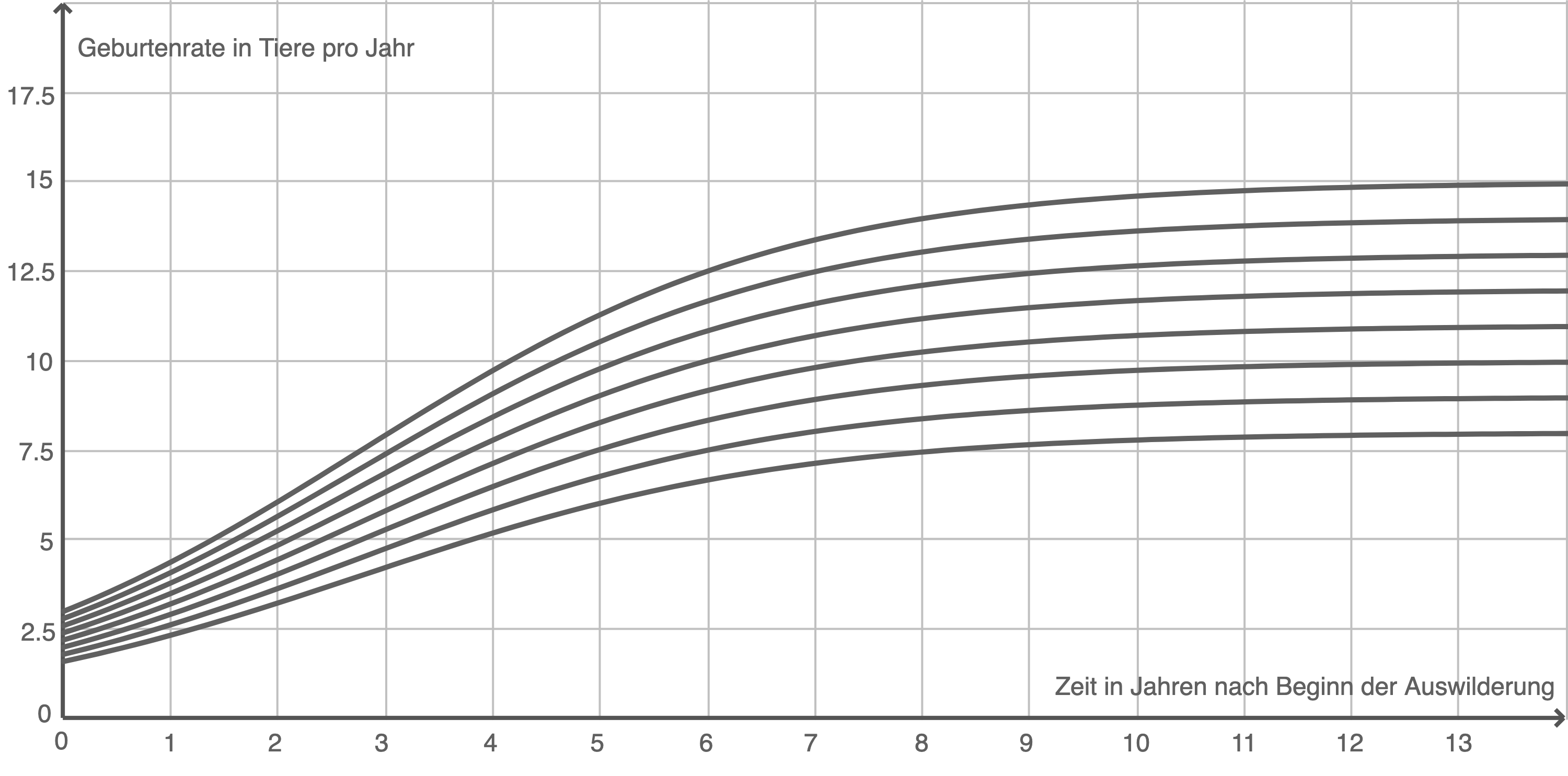
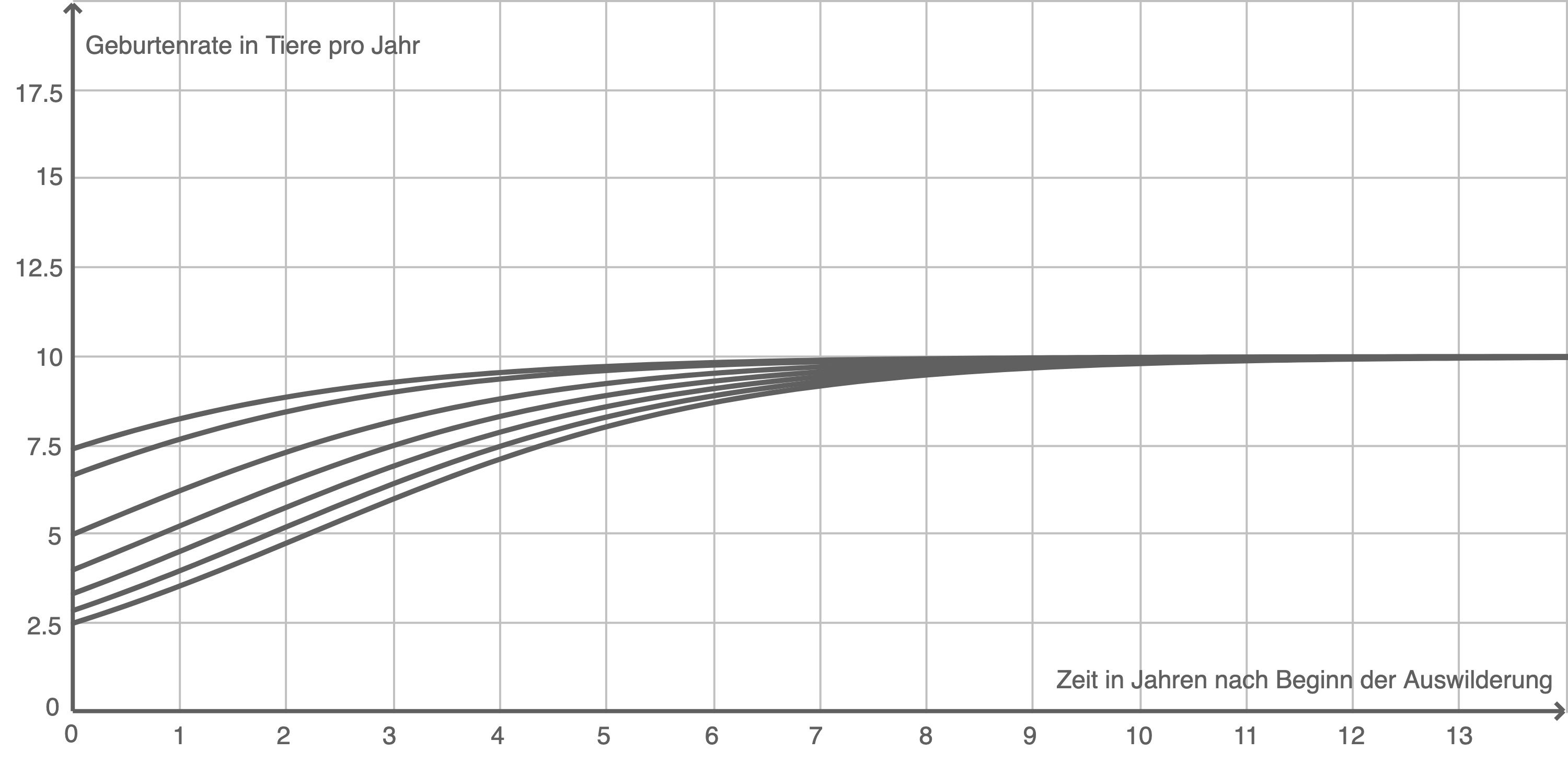

Abb. 1

Abb. 2

Abb. 3
1.1
Bestimme ohne Verwendung der Graphen für die Modelle A, B und C jeweils die Geburtenrate zum Zeitpunkt der Auswilderung sowie die langfristige Entwicklung der Geburtenrate. Gib für die Abbildungen 1 bis 3 aus Material 1 jeweils an, welchem der drei Modelle A, B und C sie zuzuordnen sind.
(6 BE)
1.2
Beschreibe unter Berücksichtigung deiner Ergebnisse aus Aufgabe 1.1, welchen Einfluss die Scharparameter 
 und
und  jeweils auf die Geburtenrate zum Zeitpunkt der Auswilderung sowie auf die langfristige Entwicklung der Geburtenrate haben.
jeweils auf die Geburtenrate zum Zeitpunkt der Auswilderung sowie auf die langfristige Entwicklung der Geburtenrate haben.
(3 BE)
2
Im Folgenden soll für die Modellierung der Geburtenrate das Modell C mit der zugehörigen Funktionsgleichung  verwendet werden.
verwendet werden.
Die Gleichung der ersten Ableitung kann ohne Nachweis verwendet werden.
kann ohne Nachweis verwendet werden.
Die Gleichung der ersten Ableitung
2.1
Berechne die Wendepunkte der Schar 
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
Beschreibe die Bedeutung der Wendestelle im Sachzusammenhang.
 Zur Kontrolle:
Zur Kontrolle: 
![\(\bigg]\)](https://mathjax.schullv.de/4b61dd2dabbb8b74e78b937540addb1f8bc242927b45ff99fcc77bdb1a7dc91d?color=5a5a5a)
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
Beschreibe die Bedeutung der Wendestelle im Sachzusammenhang.
(7 BE)
2.2
Die Wendepunkte aller Graphen der Schar liegen auf einer Kurve, der sogenannten Ortskurve. Leite für diese Ortskurve der Wendepunkte die zugehörige Funktionsgleichung her und bestätige, dass alle Wendepunkte auf einer Geraden liegen.
(4 BE)
3
Bei der Betrachtung der Populationsentwicklung ist neben der Geburtenrate auch die Sterberate zu berücksichtigen. Die Population wurde ab dem Zeitpunkt der Auswilderung über 10 Jahre beobachtet. Die Entwicklung der Geburtenrate soll durch die Funktion  der Schar
der Schar  aus Aufgabe 1 mit
aus Aufgabe 1 mit  modelliert werden, die Entwicklung der Sterberate durch die Funktion
modelliert werden, die Entwicklung der Sterberate durch die Funktion  mit
mit 
Die Graphen der Funktionen und
und  sind in Material 2 dargestellt.
Material 2
sind in Material 2 dargestellt.
Material 2
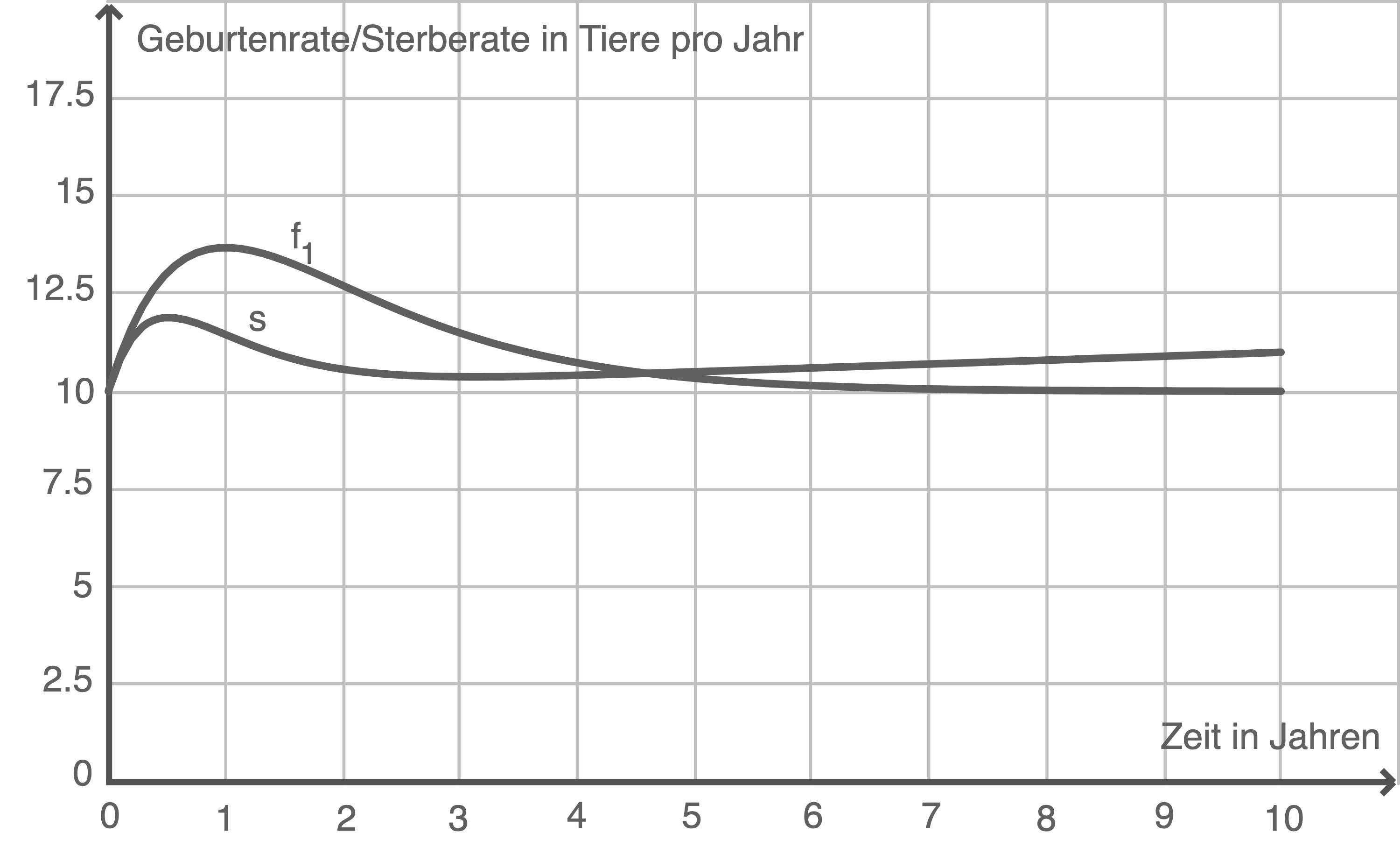
Die Graphen der Funktionen

Abb. 4
3.1
Leite mit einer geeigneten Integrationsmethode die Gleichung einer Stammfunktion  der Funktion
der Funktion  her und benenne die von dir verwendete Integrationsmethode.
her und benenne die von dir verwendete Integrationsmethode.
[Zur Kontrolle: ]
]
[Zur Kontrolle:
(5 BE)
3.2
Berechne die Anzahl der Geburten in den ersten  Jahren nach der Auswilderung.
Jahren nach der Auswilderung.
(4 BE)
3.3
Erläutere zunächst ohne Verwendung des Sachzusammenhangs die einzelnen Zeilen der unten dargestellten Rechnung. Deute anschließend den Ansatz in Zeile (1) sowie den Wert  jeweils im Sachzusammenhang.
jeweils im Sachzusammenhang.
(5 BE)
3.4
Berechne die drei Zeitpunkte, zu denen sich die Größe der Population gemäß der vorgenommenen Modellierung nicht verändert hat.
Hinweis: Ersetze an geeigneter Stelle durch
durch 
Hinweis: Ersetze an geeigneter Stelle
(6 BE)
1.1
Geburtenrate bei  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
f_a(0) &=& \dfrac{a}{1+4\cdot \mathrm e^{-0,5\cdot 0}} \\[5pt]
&=& \dfrac{a}{5} \\[10pt]
f_b(0) &=& \dfrac{10}{1+b\cdot \mathrm e^{-0,5\cdot 0}} \\[5pt]
&=& \dfrac{10}{1+b} \\[10pt]
f_c(0) &=& 10\cdot 0\cdot \mathrm e^{-c\cdot 0} +10 \\[5pt]
&=& 10 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/0885f5261df9abc6352c6e4e80638afaf49fd098d9364ee7b67c326601860de4?color=5a5a5a) Zum Zeitpunkt der Auswilderung beträgt die Geburtenrate also im Modell A
Zum Zeitpunkt der Auswilderung beträgt die Geburtenrate also im Modell A  Tiere pro Jahr, im Modell B
Tiere pro Jahr, im Modell B  Tiere pro Jahr und im Modell C
Tiere pro Jahr und im Modell C  Tiere pro Jahr.
Entwicklung der Geburtenrate bestimmen
Für
Tiere pro Jahr.
Entwicklung der Geburtenrate bestimmen
Für  gilt für den Nenner des Bruchs des Funktionsterms im Modell A:
gilt für den Nenner des Bruchs des Funktionsterms im Modell A:
 Insgesamt gilt daher
Insgesamt gilt daher  für
für  Für Modell
Für Modell  gilt ebenfalls
gilt ebenfalls  und damit
und damit  für
für  Für Modell
Für Modell  gilt:
gilt:
 Insgesamt entwickelt sich die Geburtenrate folglich nach Modell A langfristig zu
Insgesamt entwickelt sich die Geburtenrate folglich nach Modell A langfristig zu  Tiere pro Jahr und nach Modell B und Modell C zu
Tiere pro Jahr und nach Modell B und Modell C zu  Tiere pro Jahr.
Abbildungen zuordnen
Da im Modell C die Geburtenrate zum Zeitpunkt der Auswilderung unabhängig vom Parameterwert
Tiere pro Jahr.
Abbildungen zuordnen
Da im Modell C die Geburtenrate zum Zeitpunkt der Auswilderung unabhängig vom Parameterwert  Tiere pro Jahr beträgt, gehört Abbildung 1 zu Modell C.
Die langfristige Entwicklung ist nur bei Modell B und C unabhängig vom Parameter. Somit gehört Abbildung 3 also zu Modell B.
Im Modell A hängt die Geburtenate sowohl bei Auswilderung als auch auf langfrsitig vom Parameter
Tiere pro Jahr beträgt, gehört Abbildung 1 zu Modell C.
Die langfristige Entwicklung ist nur bei Modell B und C unabhängig vom Parameter. Somit gehört Abbildung 3 also zu Modell B.
Im Modell A hängt die Geburtenate sowohl bei Auswilderung als auch auf langfrsitig vom Parameter  ab. Somit lässt sich Abbildung 2 dem Modell A zuordnen.
ab. Somit lässt sich Abbildung 2 dem Modell A zuordnen.
1.2
Modell A
Die Geburtenrate zum Zeitpunkt der Auswilderung beträgt  Tiere pro Jahr.
Mit einem größeren Wert von
Tiere pro Jahr.
Mit einem größeren Wert von  steigt also auch die Geburtenrate zum Zeitpunkt der Auswilderung.
Die langfristige Entwicklung der Geburtenrate ist
steigt also auch die Geburtenrate zum Zeitpunkt der Auswilderung.
Die langfristige Entwicklung der Geburtenrate ist  Diese wird also direkt durch den Parameterwert
Diese wird also direkt durch den Parameterwert  angegeben, sodass die langfristige Geburtenrate steigt, wenn der Parameterwert von
angegeben, sodass die langfristige Geburtenrate steigt, wenn der Parameterwert von  steigt.
Modell B
Die Geburtenrate zum Zeitpunkt der Auswilderung beträgt
steigt.
Modell B
Die Geburtenrate zum Zeitpunkt der Auswilderung beträgt  Mit steigenden Werten von
Mit steigenden Werten von  sinkt also die Geburtenrate zum Zeitpunkt der Auswilderung im Modell B.
Langfristig entwickelt sich die Geburtenrate in diesem Modell gegen den Wert
sinkt also die Geburtenrate zum Zeitpunkt der Auswilderung im Modell B.
Langfristig entwickelt sich die Geburtenrate in diesem Modell gegen den Wert  Dieser ist unabhängig vom Parameter
Dieser ist unabhängig vom Parameter  Der Wert
Der Wert  hat also keinen Einfluss auf die langfristige Entwicklung der Geburtenrate.
Modell C
Die Geburtenrate zum Zeitpunkt der Auswilderung beträgt
hat also keinen Einfluss auf die langfristige Entwicklung der Geburtenrate.
Modell C
Die Geburtenrate zum Zeitpunkt der Auswilderung beträgt  und ist daher unabhängig vom Parameterwert
und ist daher unabhängig vom Parameterwert  Langfristig entwickelt sich die Geburtenrate in diesem Modell gegen dern Wert
Langfristig entwickelt sich die Geburtenrate in diesem Modell gegen dern Wert  Dieser ist unabhängig vom Parameter
Dieser ist unabhängig vom Parameter  Der Wert
Der Wert  hat also keinen Einfluss auf die langfristige Entwicklung der Geburtenrate.
hat also keinen Einfluss auf die langfristige Entwicklung der Geburtenrate.
2.1
Wendepunkte berechnen
 Durch Anwendung der Produktregel kann die zweite Ableitung berechnet werden:
1. Schritt: Notwendiges Kriterium anwenden
2. Schritt:
Durch Anwendung der Produktregel kann die zweite Ableitung berechnet werden:
1. Schritt: Notwendiges Kriterium anwenden
2. Schritt:  -Koordinate bestimmen
Einsetzen in
-Koordinate bestimmen
Einsetzen in  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_c\left(\dfrac{2}{c} \right)&=& 10\cdot \dfrac{2}{c} \cdot \mathrm e^{-c\cdot \frac{2}{c}} +10 & \\[5pt]
&=& \dfrac{20}{c} \cdot \mathrm e^{-2} +10 & \\[5pt]
&=& \dfrac{20}{c\cdot \mathrm e^{2}} + 10
\end{array}\)](https://mathjax.schullv.de/9384fcf4531890eb9476f6d0ed1e7cc0654fc6c9499b9fc142258c9a8d125677?color=5a5a5a) Der Graphen der Schar
Der Graphen der Schar  besitzten also Wendepunkte mit den Koordinaten
besitzten also Wendepunkte mit den Koordinaten  Bedeutung beschreiben
Die Wendestellen von
Bedeutung beschreiben
Die Wendestellen von  sind die Extremstellen der ersten Ableitungsfunktion
sind die Extremstellen der ersten Ableitungsfunktion  welche die Änderungsrate von
welche die Änderungsrate von  beschreibt.
Die Wendestelle gibt also den Zeitpunkt an, zu dem die Geburtenrate am stärksten abnimmt oder am stärksten zunimmt. Anhand von Abbildung 1 lässt sich erkennen, dass die Geburtenrate an dieser Stelle abnimmt. Die Wendestelle entspricht also dem Zeitpunkt im Modell C, zu dem die Geburtenrate am stärksten abnimmt.
beschreibt.
Die Wendestelle gibt also den Zeitpunkt an, zu dem die Geburtenrate am stärksten abnimmt oder am stärksten zunimmt. Anhand von Abbildung 1 lässt sich erkennen, dass die Geburtenrate an dieser Stelle abnimmt. Die Wendestelle entspricht also dem Zeitpunkt im Modell C, zu dem die Geburtenrate am stärksten abnimmt.
2.2
Umformen der  -Koordinate des Wendepunkts nach
-Koordinate des Wendepunkts nach  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
t &=& \dfrac{2}{c} &\quad \scriptsize \mid\; \cdot c \\[5pt]
t\cdot c&=& 2 &\quad \scriptsize \mid\;:t \\[5pt]
c&=& \dfrac{2}{t}
\end{array}\)](https://mathjax.schullv.de/45b62236b579dca3ac0e50a4308f6f148aadd3c5d4734e2a12a61979b92f847c?color=5a5a5a) Einsetzen in die
Einsetzen in die  -Koordinate liefert:
-Koordinate liefert:
![\(\begin{array}[t]{rll}
y_W&=& \dfrac{20}{c\cdot \mathrm e^2} +10 &\quad \scriptsize \mid\;c = \dfrac{2}{t} \\[5pt]
&=& \dfrac{20}{\frac{2}{t}\cdot \mathrm e^2} +10 \\[5pt]
&=& \dfrac{10}{\mathrm e^2}t +10\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b502359110cc951b73cdfff27d87ba0c7a6bd62a150818f996be4dce40e084f9?color=5a5a5a) Alle Wendepunkte der Schar
Alle Wendepunkte der Schar  liegen also auf dem Graphen mit der Gleichung
liegen also auf dem Graphen mit der Gleichung  Da diese Gleichung eine Gerade beschreibt, liegen folglich alle Wendepunkte der Schar
Da diese Gleichung eine Gerade beschreibt, liegen folglich alle Wendepunkte der Schar  auf einer Geraden.
auf einer Geraden.
3.1
3.2
Die Anzahl der Geburten in einem bestimmten Zeitraum kann mithilfe eines Integrals über  berechnet werden:
In den ersten zehn Jahren nach der Auswilderung finden folglich ca.
berechnet werden:
In den ersten zehn Jahren nach der Auswilderung finden folglich ca.  Geburten statt.
Geburten statt.
3.3
Rechnungen erläutern
 im ersten Schritt wird gebildet als Differenz aus der Funktion für die Geburtenrate und der Funktion für die Sterberate.
Ist diese positiv, werden mehr Tiere geboren als sterben und die Population wächst. Ist sie negativ, schrumpft die Population, da mehr Tiere sterben als geboren werden.
Durch
im ersten Schritt wird gebildet als Differenz aus der Funktion für die Geburtenrate und der Funktion für die Sterberate.
Ist diese positiv, werden mehr Tiere geboren als sterben und die Population wächst. Ist sie negativ, schrumpft die Population, da mehr Tiere sterben als geboren werden.
Durch  wird also die Änderungsrate der Größe der betrachteten Population beschrieben. Der Wert
wird also die Änderungsrate der Größe der betrachteten Population beschrieben. Der Wert  gibt daher den Zeitpunkt an, zu dem die Population am stärksten wächst.
gibt daher den Zeitpunkt an, zu dem die Population am stärksten wächst.
(1)
Es wird eine Differenzenfunktion  mit
mit  gebildet.
gebildet.
(2)
Die erste Ableitungsfunktion  von
von  wird mithilfe der Produktregel gebildet und der Funktionsterm so weit wie möglich vereinfacht.
wird mithilfe der Produktregel gebildet und der Funktionsterm so weit wie möglich vereinfacht.
(3)
Anwendung des notwendigen Kriteriums für Extremstellen von  , indem
, indem  gesetzt wird. Diese Gleichung ergibt eine Lösung
gesetzt wird. Diese Gleichung ergibt eine Lösung  Bei
Bei  handelt es sich also um eine mögliche Extremstelle von
handelt es sich also um eine mögliche Extremstelle von 
(4)
Diese mögliche Extremstelle von  wird in die zweite Ableitungsfunktion eingesetzt. Mit dem hinreichenden Kriterium ergibt sich wegen
wird in die zweite Ableitungsfunktion eingesetzt. Mit dem hinreichenden Kriterium ergibt sich wegen  dass
dass  an der Stelle
an der Stelle  ein lokales Maximum annimmt.
ein lokales Maximum annimmt.
Ansatz im Sachzusammenhang deuten
Die Differenzenfunktion
3.4
Die Zeitpunkte, zu denen sich die Größe der Population nicht ändert, werden durch die Nullstellen der Funktion  aus Aufgabe 3.3 beschrieben:
Mit dem Satz vom Nullprodukt folgt
aus Aufgabe 3.3 beschrieben:
Mit dem Satz vom Nullprodukt folgt  Berechnen der Werte für
Berechnen der Werte für  :
:
![\(\begin{array}[t]{rll}
10\cdot\mathrm e^{-t}-10\cdot \mathrm e^{-2\cdot t}-0,1 &=& 0 &\quad \scriptsize \mid\; :(-10) \\[5pt]
-\mathrm e^{-t}+\left(\mathrm e^{-t}\right)^2+0,01 &=& 0 \\[5pt]
\left(\mathrm e^{-t}\right)^2-\mathrm e^{-t}+0,01 &=& 0 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3288ea0cae853d4b4d4f1f2ae66eb506c5c65cc45f9f106558ff587cdae0d8f6?color=5a5a5a) Durch Substitution mit
Durch Substitution mit  folgt:
folgt:
 Durch Anwenden der p-q-Formel ergibt sich:
Durch Anwenden der p-q-Formel ergibt sich:
![\(\begin{array}[t]{rll}
z_{1/2} &=& -\dfrac{(-1)}{2}\pm \sqrt{\left(\dfrac{-1}{2} \right)^2 -0,01} \\[5pt]
z_{1/2} &=& 0,5\pm \sqrt{0,24} & \\[5pt]
z_1 &=& 0,5+\sqrt{0,24} \\[5pt]
z_2 &=& 0,5-\sqrt{0,24} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/8d4697d7d897f08a60bba6be55dc5ffe250c052884c5ba5ad32f42383eb2da03?color=5a5a5a) Resubstitution liefert nun:
Resubstitution liefert nun:
![\(\begin{array}[t]{rll}
z_1&=& \mathrm e^{-t_2} \\[5pt]
0,5+\sqrt{0,24}&=& \mathrm e^{-t_2} &\quad \scriptsize \mid\;\ln \\[5pt]
\ln \left(0,5+\sqrt{0,24}\right)&=& -t_2 &\quad \scriptsize \mid\;\cdot (-1) \\[5pt]
-\ln \left(0,5+\sqrt{0,24}\right)&=& t_2 \\[5pt]
0,01 &\approx& t_2
\end{array}\)](https://mathjax.schullv.de/ac8880cdc7d85b254541c3f683ec53559446112c43b894273887df29e65b44c4?color=5a5a5a)
![\(\begin{array}[t]{rll}
z_2&=& \mathrm e^{-t_3} \\[5pt]
0,5-\sqrt{0,24}&=& \mathrm e^{-t_3} &\quad \scriptsize \mid\;\ln \\[5pt]
\ln \left(0,5-\sqrt{0,24}\right)&=& -t_3 &\quad \scriptsize \mid\;\cdot (-1) \\[5pt]
-\ln \left(0,5-\sqrt{0,24}\right)&=& t_3 \\[5pt]
4,60 &\approx& t_3 \\[10pt]
\end{array}\)](https://mathjax.schullv.de/7d036948f4772f07c4f77774df0d7048ddb55d1fa72ec8aa7cc91120b3e5f6e7?color=5a5a5a) Zum Zeitpunkt der Auswilderung, ca.
Zum Zeitpunkt der Auswilderung, ca.  Jahre danach und ca.
Jahre danach und ca.  Jahre nach der Auswilderung hat sich die Größe der Population gemäß der vorgenommenen Modellierung nicht verändert.
Jahre nach der Auswilderung hat sich die Größe der Population gemäß der vorgenommenen Modellierung nicht verändert.