B2 - Analytische Geometrie

Im Material ist die Bühne eines Musicaltheaters schematisch dargestellt. Aus dem Zuschauerraum führt eine Rampe zur Bühne. Die Punkte $A(6\mid0\mid -1),$ $B(7 \mid 2 \mid -1),$ $C(1\mid5\mid0,25)$ und $D(0 \mid3\mid0,25)$ sind die Eckpunkte dieser Rampe. Eine Einheit entspricht einem Meter.

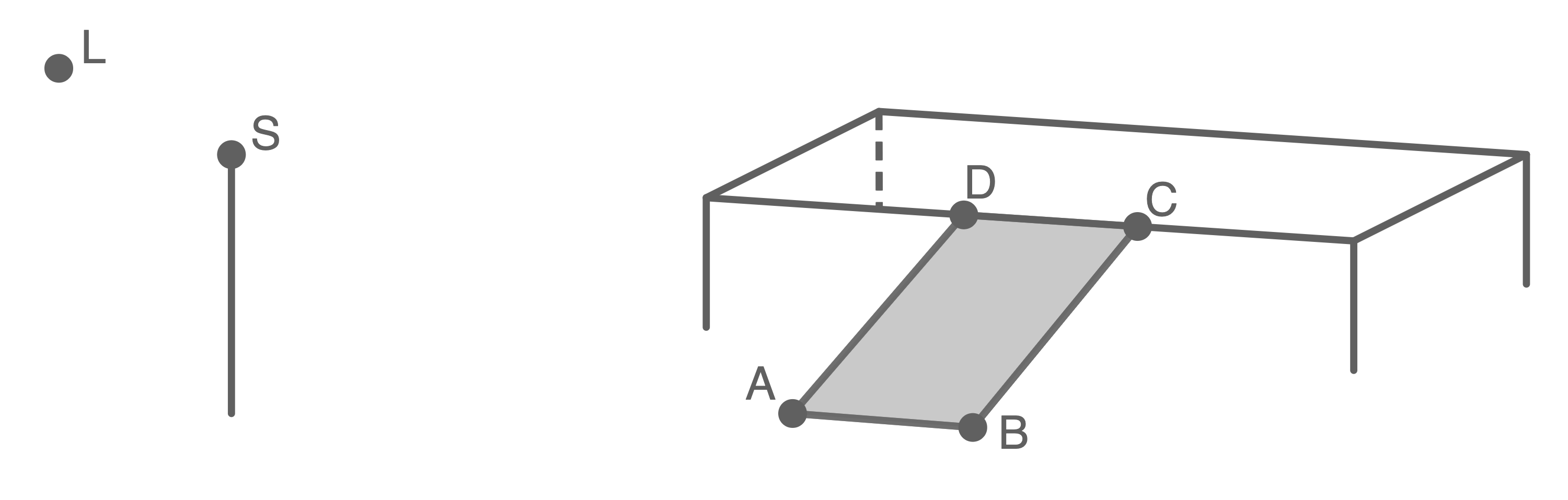
Material

1.1

Zeige, dass die Rampe $ABCD$ ein Rechteck ist.

(3 BE)

1.2

Bestimme eine Parameter- sowie eine Koordinatengleichung der Ebene $E,$ in der die Rampe liegt.
[Zur Kontrolle: $2,5x - 1,25y + 15z = 0$ ist eine mögliche Koordinatengleichung von $E.$ ]

(6 BE)

1.3

Bestimme den Steigungswinkel der Rampe gegenüber der $x$ - $y$ -Ebene.

(2 BE)

Der Punkt $F(5\mid -4,5\mid -1)$ ist der Fußpunkt eines Masts, der Punkt $S(5\mid -4,5 \mid 2,5)$ stellt die Mastspitze dar. Das Licht eines Scheinwerfers breitet sich vom Punkt $L(6 \mid -7,5\mid 3,5)$ geradlinig aus, sodass der Mast einen Schatten auf die Rampe wirft.

2.1

Ermittle, ob der Schattenpunkt der Spitze $S$ des Mastes auf der Rampe $ABCD$ liegt.

(6 BE)

2.2

Gegeben ist die folgende Geradenschar $g_a$ mit

$g_a:\, \overrightarrow{x}_a = ...$

Vollständige Lösung anzeigen

Beschreibe die Bedeutung der einzelnen Vektoren sowie die Bedeutung der Geradenschar $g_a$ jeweils im Sachzusammenhang.

(4 BE)

Durch weitere Beleuchtungsanlagen in dem Musicaltheater fallen zusätzlich parallel zueinander verlaufende Lichtstrahlen in Richtung $\overrightarrow{v} = \pmatrix{-1\\2\\-0,5}$ auf die Rampe.

3.1

Bestimme die Abbildungsmatrix $P$ der Parallelprojektion durch die Lichtstrahlen auf die Rampenebene.

(7 BE)

3.2

Für die Projektionsmatrix $P$ gilt: $P^2 = P$
Erläutere die geometrische Bedeutung dieser Gleichung.

(2 BE)

1.1

In einem Rechteck müssen zwei gegenüberliegende Seiten parallel und gleich lang sein, sowie zwei benachbarte Seiten im rechten Winkel zueinander stehen.

$\begin{array}[t]{rll} \overrightarrow{AB}&=& \pmatrix{1\\2\\0} \\[5pt] \overrightarrow{DC}&=& \pmatrix{1\\2\\0} \\[5pt] \end{array}$

Es gilt also $\overrightarrow{AB} = \overrightarrow{DC}.$ Da die gegenüberliegenden Seiten $\overline{AB}$ und $\overline{DC}$ also parallel und gleichlang sind,müssen auch die beiden anderen gegenüberliegenden Seiten $\overline{BC}$ und $\overline{DA}$ gleichlang und parallel zueinander sein.

Zu überprüfen bleibt noch die Rechtwinkligkeit. Ist einer der Innenwinkel ein rechter Winkel, sind wegen der bereits gezeigten Eigenschaften auch die übrigen Innenwinkel rechtwinklig.

$\begin{array}[t]{rll} \overrightarrow{AB} \circ \overrightarrow{BC}&=&\pmatrix{1\\2\\0}\circ \pmatrix{-6\\3\\1,25} &\\[5pt] &=& 1\cdot (-6) +2\cdot 3 +0\cdot 1,25 &\\[5pt] &=& 0 \end{array}$

Die Seiten $\overline{AB}$ und $\overline{BC}$ schließen also einen rechten Winkel ein.

Bei dem Viereck $ABCD$ handelt es sich folglich insgesamt um ein Rechteck.

1.2

Parametergleichung bestimmen

Als Stützpunkt kann einer der vier Eckpunkte benutzt werden.

Die Spannvektoren ergeben sich aus den Verbindungsvektoren.

Somit folgt beispielsweise:

$E:\; \overrightarrow{x}= \overrightarrow{OA} + r \cdot \overrightarrow{AB} +s\cdot \overrightarrow{BC}$

Parametergleichung anzeigen

Koordinatengleichung bestimmen

Ein Normalenvektor von $E$ kann aus dem Kreuzprodukt der beiden Spannvektoren berechnet werden:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \pmatrix{1\\2\\0}\times \pmatrix{-6\\3\\1,25} \\[5pt] &=& \pmatrix{2\cdot 1,25 - 0\cdot 3 \\ 0\cdot (-6) - 1\cdot 1,25 \\ 1\cdot 3 - 2\cdot (-6)} \\[5pt] &=& \pmatrix{2,5\\-1,25 \\ 15} \end{array}$

Mit einer Punktprobe ergibt sich:

Rechenweg anzeigen

$d=0$

Eine Koordinatengleichung von $E$ lautet also:

$E:\; 2,5x -1,25y +15z = 0$

1.3

Ein Normalenvektor der $x$ - $y$ -Ebene ist $\overrightarrow{n}_{xy} = \pmatrix{0\\0\\1}.$ Ein Normalenvektor $\overrightarrow{n}$ der Rampe wurde in Aufgabe 1.2 berechnet.

Mit der Formel für den Schnittwinkel $\alpha$ zweier Ebenen folgt:

Rechenweg anzeigen

$\alpha \approx 10,6^{\circ}$

Der Steigungswinkel der Rampe gegenüber der $xy$ -Ebene ist folglich etwa $10,6^{\circ}$ groß.

2.1

1. Schritt: Geradengleichung der Lichtstrahlen ermitteln

Die Gerade der Lichtstrahlen verläuft durch den Punkt $S$ entlang des Vektors $\overrightarrow{LS}:$

$\begin{array}[t]{rll} l:\; \overrightarrow{x} &=& \overrightarrow{OL} +t\cdot \overrightarrow{LS} \\[5pt] &=& \pmatrix{6\\-7,5\\3,5} +t\cdot \pmatrix{-1\\3\\ -1} \end{array}$

2. Schritt: Schnittpunkt bestimmen

Durch Gleichsetzen der Geradengleichung mit der Parameterdarstellung der Ebene $E$ folgt:

Rechenweg anzeigen

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& 0 &=& r-6s+t \\ \text{II}\quad& -7,5 &=& 2r + 3s - 3t \\ \text{III}\quad& 4,5 &=& 1,25s+t & \\ \end{array}$

Aus der dritten Gleichung folgt: $\; 4,5-1,25s=t$

Durch Einsetzen von $t$ in $\text{I}$ und $\text{II}$ ergibt sich :

Rechenweg anzeigen

$s= \frac{12}{17}$

Einsetzen von $s$ in $\(\text{I$ liefert:

$\begin{array}[t]{rll} -4,5 &=& r-7,25s &\quad \scriptsize \mid\;s = \frac{12}{17} \\[5pt] -4,5 &=& r -7,25\cdot \frac{12}{17} \\[5pt] -4,5 &=& r -\frac{87}{17} &\quad \scriptsize \mid\;+\frac{87}{17} \\[5pt] \frac{21}{34}&=& r \end{array}$

Einsetzen in die Darstellung für $t$ ergibt:

$t =4,5-1,25\cdot \frac{12}{17} = \frac{123}{34}$

3. Schritt: Lage des Schattenpunktes ermitteln

Durch Einsetzen der Parameter $r$ und $s$ in die Parametergleichung der Ebene $E$ kann der Schattenpunkt bestimmt werden:

$\(\begin{array}[t]{rll} \overrightarrow{OS$

Da sich der Ortsvektor des Schattenpunkts $S‘$ als Linearkombination aus $\overrightarrow{AB}$ und $\overrightarrow{BC}$ mit $0\leq r \leq 1$ und $0\leq s \leq 1$ darstellen lässt, liegt der Punkt $S‘$ in dem von $A,$ $B$ und $C$ aufgespannten Rechteck.

Der Schattenpunkt der Mastspitze liegt also auf der Rampe.

2.2

Der Vektor $\pmatrix{6\\-7,5\\3,5}$ ist der Ortsvektor des Punkts $L,$ von dem aus sich das Licht des Schweinwerfers ausbreitet

Der Vektor $\pmatrix{5\\-4,5\\-1+a}$ ist der Ortsvektor eines Punkts $P_a$ , der für $0\leq a\leq 3,5$ einen Punkt auf dem Mast darstellt.

Der Vektor $\pmatrix{5\\-4,5\\-1+a}-\pmatrix{6\\-7,5\\3,5}$ ist demnach für $0\leq a\leq 3,5$ der Verbindungsvektor zwischen dem Punkt $L,$ von dem aus sich das Licht ausbreitet, und dem Punkt $P_a$ auf dem Mast. Er gibt also die Richtung an, in der die Lichtstrahlen vom Scheinwerfer aus in Richtung eines bestimmten Punkts $P_a$ auf dem Mast fallen.

Insgesamt beschreiben die Geraden $g_a$ daher jeweils für die Punkte $P_a$ auf dem Mast den Verlauf des Lichts, das vom Scheinwerfer aus in diesem Punkt auf den Mast trifft.

3.1

Durch die Abbildungsmatrix $P$ soll der Punkt $X(x\mid y\mid z)$ entlang des Vektors $\overrightarrow{v} = \pmatrix{-1\\2\\-0,5}$ auf die Ebene $E$ projiziert werden. Der dabei entstehende Bildpunkt $X‘$ von $X$ ist der Schnittpunkt der Geraden durch $X$ entlang des Vektors $\overrightarrow{v}$ mit der Ebene $E.$

Durch Ermitteln der Bildpunkte von $(1\mid 0\mid0),$ $(0\mid 1\mid 0)$ und $(0\mid 0\mid 1)$ kann auf die Abbildungsmatrix geschlossen werden.

1. Schritt: Bildpunkt von $(1\mid 0\mid 0)$ bestimmen

Die Gerade, entlang derer der Punkt $(1\mid 0\mid 0)$ projiziert wird, kann durch folgende Gleichung beschrieben werden:

$\(\overrightarrow{x$

Einsetzen der Koordinaten in die Koordinatengleichung von $E$ liefert:

Rechenweg anzeigen

$t=0,2$

Durch Einsetzen von $t$ in die Geradengleichung folgt der Bildpunkt von $(1\mid 0\mid 0)$ mit $(0,8\mid0,4\mid-0,1).$

2. Schritt: Bildpunkt von $(0\mid 1\mid 0)$ bestimmen

Die Gerade, entlang derer der Punkt $(0\mid 1\mid 0)$ projiziert wird, kann durch folgende Gleichung beschrieben werden:

$\overrightarrow{x‘} = \pmatrix{0\\1\\0} +t\cdot \pmatrix{-1\\2\\-0,5} = \pmatrix{-t\\1+2t\\-0,5t}$

Einsetzen der Koordinaten in die Koordinatengleichung von $E$ liefert:

Rechenweg anzeigen

$t=-0,1$

Der Bildpunkt von $(0\mid 1\mid 0)$ ist also $(0,1\mid0,8\mid0,05).$

3. Schritt: Bildpunkt von $\boldsymbol{(0\mid 0\mid 1)}$ bestimmen

Die Gerade, entlang derer der Punkt $(0\mid 0\mid 1)$ projiziert wird, kann durch folgende Gleichung beschrieben werden:

$\overrightarrow{x‘} = \pmatrix{0\\0\\1} +t\cdot \pmatrix{-1\\2\\-0,5} = \pmatrix{-t\\2t\\1-0,5t}$

Einsetzen der Koordinaten in die Koordinatengleichung von $E$ liefert:

Rechenweg anzeigen

$t=1,2$

Der Bildpunkt von $(0\mid 0\mid 1)$ ist also $(-1,2\mid2,4\mid0,4).$

4. Schritt: Abbildungsmatrix bestimmen

Für den ersten Punkt und seinen Bildpunkt muss folgende Gleichung erfüllt werden:

$\underbrace{\pmatrix{p_{11} & p_{12} & p_{13} \\p_{21} & p_{22} & p_{23} \\p_{31} & p_{32} & p_{33} }}_P \cdot \pmatrix{1\\0\\0} = \pmatrix{0,8\\0,4\\-0,1}$

Es müssen also folgende Gleichungen erfüllt werden:

Gleichungssystem anzeigen

Durch Lösen der entsprechenden Gleichungssysteme für die übrigen beiden Punkte $(0\mid 1\mid 0)$ und $(0\mid 0\mid 1)$ und die zugehörigen Bildpunkte folgt:

$P = \pmatrix{0,8 &0,1& -1,2 \\ 0,4 & 0,8 &2,4 \\ -0,1 & 0,05 & 0,4 }$

3.2

Eine Multiplikation mit $P^2$ bedeutet eine zweimalige Anwendung der Abbildung. Nachdem die Projektion auf die Rampenebene also einmal durchgeführt wurde, wird sie nochmals durchgeführt. Da sich das projizierte Objekt dann bereits in der Rampenebene befindet, sollte eine nochmalige Ausführung der Projektion keine weitere Veränderung bewirken.

Dies ist durch $P^2=P$ gegeben. Die zweimalige und dadurch auch mehrmalige Anwendung der Abbildung führt zu keiner Veränderung im Vergleich zur einmaligen Anwendung. Das Objekt wird also nur einmal auf die Ebene projiziert und dann nicht weiter durch die Abbildung verändert. Befindet sich ein Objekt bereits in der Rampenebene werden seine Koordinaten durch die Projektion nicht verändert. Es wird also auf sich selbst abgebildet.