B2 - Analytische Geometrie

In einem Wohnhaus, dessen Hauswand in der $y$ - $z$ -Ebene liegt, wird über einer rechteckigen, in der $x$ - $y$ -Ebene gelegenen Fläche $ABCD$ eine Terrasse gebaut (Material). Dabei ist $C$ der Ursprung des Koordinatensystems.
Um Regenwasser sicher vom Haus fernzuhalten, hat die ebene Oberfläche $A_1B_1C_1D_1$ der Terrasse entlang aller Kanten gegenüber der $x$ - $y$ -Ebene jeweils ein Gefälle von $1,5\,\%.$
Die Koordinaten der Eckpunkte der Terrasse lauten $A_1= A(6\mid 12\mid 0)$ , $B_1(0\mid 12\mid 0,09)$ , $C_1(0\mid 0\mid0,27)$ , $D_1(6\mid 0\mid z_{D1}).$ Die Punkte $B_1$ , $C_1$ , $D_1$ liegen in vertikaler Richtung jeweils oberhalb der Punkte $B, C, D.$
Eine Längeneinheit entspricht einem Meter.

1.1

Gib die Koordinaten der Punkte $B$ und $D$ an und berechne die fehlende Koordinate $z_{D1}$ des Punktes $D_1$ .

(4 BE)

1.2

Zeige, dass die Oberfläche der Terrasse in der Ebene $T:\; 3x+3y+200z = 54$ liegt.

(4 BE)

1.3

Um zu erreichen, dass Wasser gut ablaufen kann, wird ein Gefälle der Terrassenoberfläche gegenüber der $x$ - $y$ -Ebene von mindestens $2\,\%$ empfohlen. Prüfe, ob diese Bedingung erfüllt ist.

(5 BE)

Entlang der Hauswand wird eine rechteckige Teilüberdachung der Terrasse mit den Eckpunkten $P_1(3\mid 1\mid 2,4), P_2, H_2(0\mid 9\mid 2,5)$ und $H_1(0\mid 1\mid 2,5)$ angebracht (Material).
Die Teilüberdachung ist über zwei Stahlseile in den Punkten $S_1$ , $S_2$ an der Hauswand befestigt. Dabei liegt der Punkt $S_1$ vertikal über $H_1$ und der Punkt $S_2$ vertikal über $H_2$ .

Material

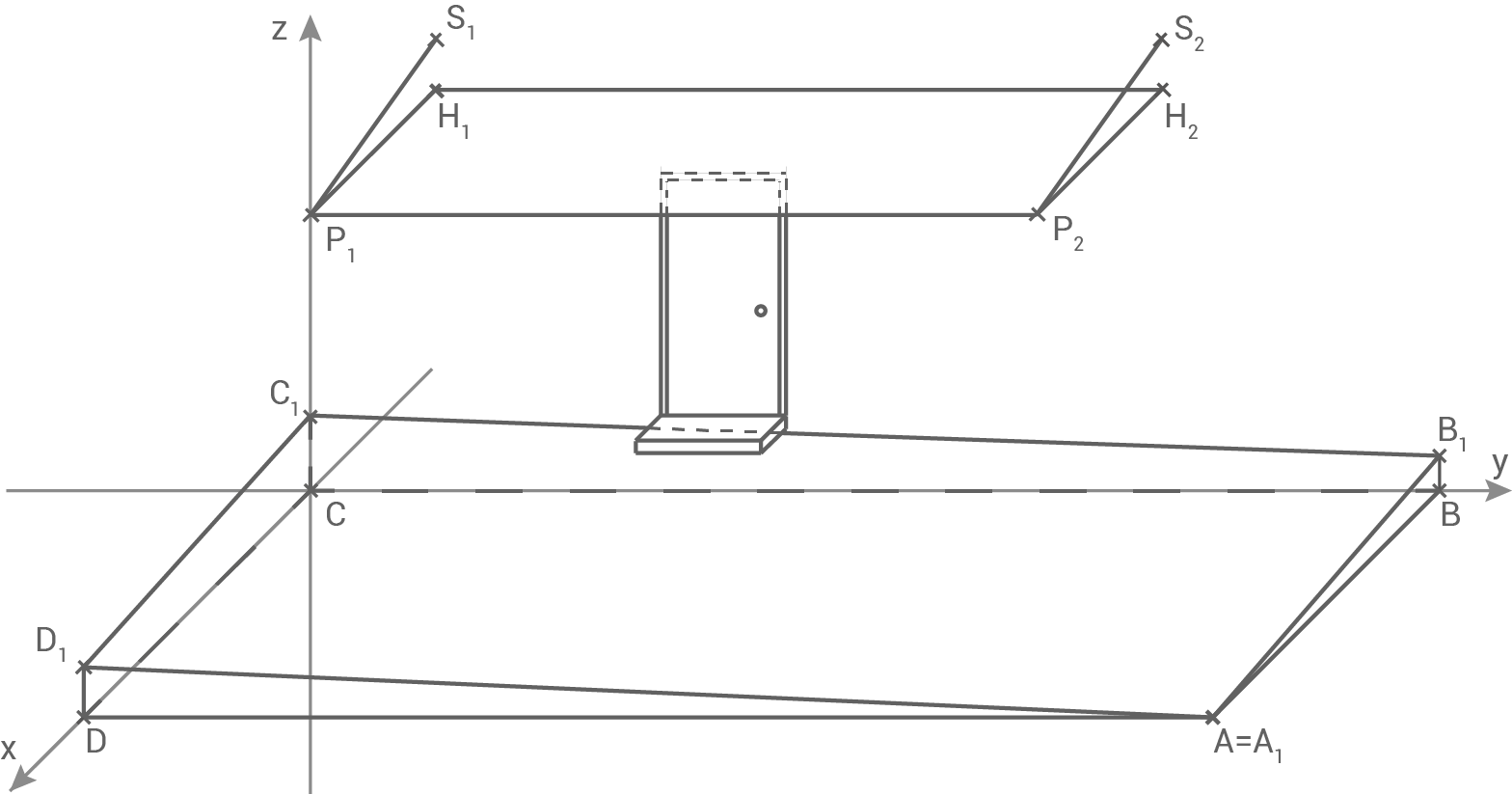Hinweis: Die Abbildung ist nicht maßstabsgerecht.

2.1

Regenwasser auf der Überdachung soll von $P_1$ durch ein vertikal verlaufendes Fallrohr geleitet werden. Hierfür muss die Terrassenoberfläche durchbohrt werden. Bestimme den Punkt $G$ , in dem die Bohrung auf der Terrassenoberfläche vorgenommen werden muss.

(4 BE)

2.2

Die Stahlseile der Überdachung sollen so an der Hauswand befestigt werden, dass der Winkel $\beta$ zwischen dem von $S_1$ nach $P_1$ verlaufenden Stahlseil und der Hauswand $60^{\circ}$ beträgt.
Untersuche, wie die Koordinaten des Verankerungspunkts $S_1$ gewählt werden müssen.

(5 BE)

Die Koordinaten der Punkte der Terrassenoberfläche, die in vertikaler Richtung unterhalb der Überdachung liegen, erhält man mithilfe einer Abbildung, die jeden Punkt des Rechtecks $P_1P_2H_2H_1$ parallel zur $z$ -Achse auf die Ebene $T$ projiziert.

3.1

$T_1$ ist diejenige Ebene, die parallel zur Ebene $T$ und durch den Punkt $C(0\mid 0\mid 0)$ verläuft. Bestimme die Abbildungsmatrix $M$ einer Abbildung, mit deren Hilfe alle Punkte des Raums parallel zur $z$ -Achse auf $T_1$ projiziert werden.

(6 BE)

3.2

Stelle die Abbildung, mit deren Hilfe man die Koordinaten der Punkte der Terrassenoberfläche, die in vertikaler Richtung unterhalb der Überdachung liegen, bestimmen kann, in der Form $\(\overrightarrow{x}$ dar.

(2 BE)

1.1

Koordinaten angeben

1. Schritt: Koordinaten von $B$ und $D$ angeben

$B(0\mid 12\mid 0)$

$D(6\mid 0 \mid 0)$

2. Schritt: $z_{D_1}$ berechnen

Das Gefälle der Kante $\overline{D_1A_1}$ gegnüber der $x$ - $y$ -Ebene beträgt $1,5\,\%.$ und das Dreieck $D_1DA_1$ besitzt einen rechten Winkel bei $D$ .
Ein Gefälle von $1,5\,\%$ bedeutet eine vertikale Differenz von $1,5\,\text{LE}$ auf einer horizontalen Strecke der Länge $100\,\text{LE}$ . Die Strecke $\overline{DA_1}$ besitzt eine Länge von $12\,\text{LE},$ somit muss die vertikale Differenz hier $0,18\,\text{LE}$ betragen, da pro Längeneinheit ein Gefälle von $0,015\,\text{LE}$ in vertikale Richtung erfolgt.
Es folgt damit für $D_1:$

$D_1(6\mid 0\mid 0,18)$

1.2

Lage der Oberfläche zeigen

Die Oberfläche ist eben und wird von den vier Eckpunkten $A_1$ , $B_1$ , $C_1$ und $D_1$ begrenzt. Mit Hilfe von Punktproben zeigen, dass die vier Eckpunkte in der Ebene liegen:

1. Schritt: $A_1$ einsetzen

Rechenweg anzeigen

$54 = 54$

$A_1$ liegt in $T.$

2. Schritt: $B_1$ einsetzen:

Rechenweg anzeigen

$54 = 54$

$B_1$ liegt in $T.$

3. Schritt: $C_1$ einsetzen:

Rechenweg anzeigen

$54 = 54$

$C_1$ liegt in $T.$

4. Schritt: $D_1$ einsetzen:

Rechenweg anzeigen

$54 = 54$

$D_1$ liegt ebenfalls in $T.$ Somit liegt die komplette Oberfläche der Terasse in $T.$

1.3

Ein Normalenvektor der $x$ - $y$ -Ebene ist $\overrightarrow{n}_1 = \pmatrix{0\\0\\1}.$

Einen Normalenvektor von $T$ wird aus der Ebenengleichung abgelesen: $\overrightarrow{n}_2 = \pmatrix{3\\3\\200}.$

Es folgt für den Schnittwinkel der Ebenen:

Rechenweg anzeigen

$\alpha \approx 1,215^{\circ}$

Mithilfe des Tangens wird aus diesem die Prozentangabe des Gefälles bestimmt:

Rechenweg anzeigen

$\tan(\alpha) \gt 2\,\%$

Damit ist die Bedingung erfüllt.

2.1

Bohrungspunkt bestimmen

Der Punkt $G$ , in dem gebohrt werden soll, liegt in der Terrassenoberfläche, also in der Ebene $T$ und vertikal unter dem Punkt $P_1,$ das heißt er besitzt die gleiche $x$ - und $y$ -Koordinate wie dieser.
Einsetzen der $x$ - und $y$ -Koordinaten von $P_1(3\mid 1\mid 2,4)$ in die Ebenengleichung von $T$ und auflösen nach $z$ liefert:

Rechenweg anzeigen

$z = 0,21$

Somit ergeben sich die Koordinaten $G(3\mid 1\mid 0,21).$

2.2

Koordinaten des Verankerungspunkts untersuchen

Die Hauswand liegt in der $y$ - $z$ -Ebene. Ein Normalenvektor dieser ist $\overrightarrow{n} = \pmatrix{1\\0\\0}$ .

Als Richtungsvektor der Geraden kann $\overrightarrow{P_1S_1}$ verwendet werden. Da $S_1$ vertikal über dem Punkt $H_1$ liegt hat $S_1$ die gleichen $x$ - und $y$ -Koordinaten wie dieser: $S_1(0\mid 1 \mid z_{S_1})$ .

Für den Richtungsvektor folgt damit:

$\overrightarrow{r} = \pmatrix{-3\\0\\z_{S_1}-2,4}$

Einsetzen und nach $z_{S_1}$ umformen liefert:

$\begin{array}[t]{rll} \sin (60^{\circ})&=& \dfrac{\left|\overrightarrow{n}\circ \overrightarrow{r} \right|}{\left|\overrightarrow{n} \right| \cdot \left|\overrightarrow{r} \right|} \\[5pt] \sin (60^{\circ})&=& \dfrac{\left|\pmatrix{1\\0\\0}\circ \pmatrix{-3\\0\\z_{S_1}-2,4} \right|}{\left|\pmatrix{1\\0\\0} \right| \cdot \left|\pmatrix{-3\\0\\z_{S_1}-2,4} \right|} \\[5pt] \sin (60^{\circ})&=& \dfrac{3}{1 \cdot \sqrt{(-3)^2+0^2+(z_{S_1}-2,4)^2}} \\[5pt] \sin (60^{\circ})&=& \dfrac{3}{\sqrt{9+(z_{S_1}-2,4)^2}}&\quad \scriptsize \mid\;\cdot \dfrac{ \sqrt{9+(z_{S_1}-2,4)^2}}{\sin (60^{\circ})}\\[5pt] \sqrt{9+(z_{S_1}-2,4)^2}&=& \dfrac{3}{\sin (60^{\circ})} &\quad \scriptsize \mid\;^2 \\[5pt] 9+(z_{S_1}-2,4)^2&=&\dfrac{9}{\left(\sin (60^{\circ})\right)^2} \\[5pt] 9+ z_{S_1}^2-4,8z_{S_1}+ 5,76&=& \dfrac{9}{\left(\sin (60^{\circ})\right)^2} &\quad \scriptsize \mid\;-\dfrac{9}{\left(\sin (60^{\circ})\right)^2} \\[5pt] z_{S_1}^2-4,8z_{S_1}+14,76-\dfrac{9}{\left(\sin (60^{\circ})\right)^2}&=&0\\[5pt] \end{array}$

Mithilfe der $pq$ -Formel folgt:

Rechenweg anzeigen

\begin{array}[t]{rll} z_1&\approx& 4,132 \\[5pt] z_2&\approx& 0,67 \\[5pt] \end{array} 

Die $z$ -Koordinate von $S_1$ muss größer sein als die von $H_1$ , da $S_1$ vertikal über $H_1$ liegt. $z_1$ ist somit die für den Sachverhalt richtige Lösung.

Es gilt: $S_1(0\mid 1\mid 4,132).$

3.1

Abbildungsmatrix bestimmen

Bei einer Projektion aller Punkte auf $T_1$ , die parallel zur $z$ -Achse durchgeführt wird, bleiben die $x$ - und $y$ -Koordinaten der Punkte erhalten, es ändern sich nur die $z$ -Koordinaten so, dass die Punkte in $T_1$ liegen.

1. Schritt: Ebenengleichung von $T_1$ aufstellen

$T_1$ liegt parallel zu $T$ und besitzt somit den gleichen Normalenvektor. Einsetzen der Koordinaten von $C$ für die Bestimmung der rechten Seite von $T_1$ liefert:

$3\cdot 0+3\cdot 0 +200\cdot 0 = 0$

Die Ebenengleichung lautet $T_1:\; 3x+3y+200z = 0.$

2. Schritt: Projektionsgleichung aufstellen

Es soll $\(M\cdot \overrightarrow{p} = \overrightarrow{p}$ gelten, das heißt:

$\(M\cdot \pmatrix{x\\y\\z} = \pmatrix{x$

Wie oben beschrieben gilt $\(x$ und $\(y$ . Auflösen der Ebenengleichung von $T_1$ nach $\(z$ liefert:

Rechenweg anzeigen

$\( z$

Durch Einsetzen in die Projektionsgleichung folgt:

Rechenweg anzeigen

$M\cdot \pmatrix{x\\y\\z} = ...$

3. Schritt: Einträge der Matrix bestimmen

Die $x$ - bzw. $y$ -Werte sollen jeweils auf sich selbst abgebildet werden, somit folgt für die ersten beiden Zeilen von $M:$

$M= \pmatrix{1 & 0 & 0 \\0 & 1 & 0\\ a & b & c}$

Die letzte Zeile muss $\pmatrix{x\\y\\z}$ auf $-0,015x-0,015y$ abbilden. Ausmultiplizieren liefert:

$a\cdot x +b\cdot y +c\cdot z$
$= -0,015x-0,015y$

Durch Koeffizientenvergleich folgt $a= -0,015$ , $b= -0,015$ und $c =0$ . M ist damit gegeben durch:

$M= \pmatrix{1 & 0 & 0 \\0 & 1 & 0\\ -0,015 & -0,015 & 0}$

3.2

Abbildung darstellen

Die im Aufgabenteil zuvor bestimmte Abbildungsmatrix M wird nun verwendet, um die gesuchte Abbildung der Form $\(\overrightarrow{x}$ zu benennen.

Da die Ebene $T$ parallel zur Ebene $T_1$ steht, müssen die Punkte nach der Abbildung auf die Ebene $T_1$ nur noch mit Hilfe des Vektors $\overrightarrow{k}$ verschoben werden. Da $T_1$ und $T$ die gleichen $x$ - und $y$ -Werte besitzen, findet diese Verschiebung entlang der $z$ -Achse statt.

Da der Punkt $C$ in $T_1$ vertikal unter dem Punkt $C_1$ der Ebene $T$ liegt, folgt durch Vergleich der Koordinaten der beiden Punkte und der Parallelität der Ebenen, dass $T$ aus $T_1$ durch eine Verschiebung um $0,27 \, \text{LE}$ in $z$ -Richtung entsteht. Insgesamt ergibt sich damit folgende Gleichung:

$\(\overrightarrow{x}$