B2 - Analysis
1
Wissenschaftler untersuchen auf einer Insel über einen großen Zeitraum hinweg eine Elchpopulation. Die Entwicklung der Anzahl der Elche innerhalb der ersten 50 Jahre ist in Abbildung 1 dargestellt.
Im Folgenden wird die Anzahl der Elche in verschiedenen Zeiträumen durch die Funktionen  ,
,  und
und  modelliert.
Dabei bezeichnet
modelliert.
Dabei bezeichnet  die Zeit in Jahren nach Beginn der Untersuchung zum Zeitpunkt
die Zeit in Jahren nach Beginn der Untersuchung zum Zeitpunkt  jeweils die Anzahl der Elche.
Die Graphen der drei Funktionen sind abschnittweise in Abbildung 2 dargestellt.
jeweils die Anzahl der Elche.
Die Graphen der drei Funktionen sind abschnittweise in Abbildung 2 dargestellt.
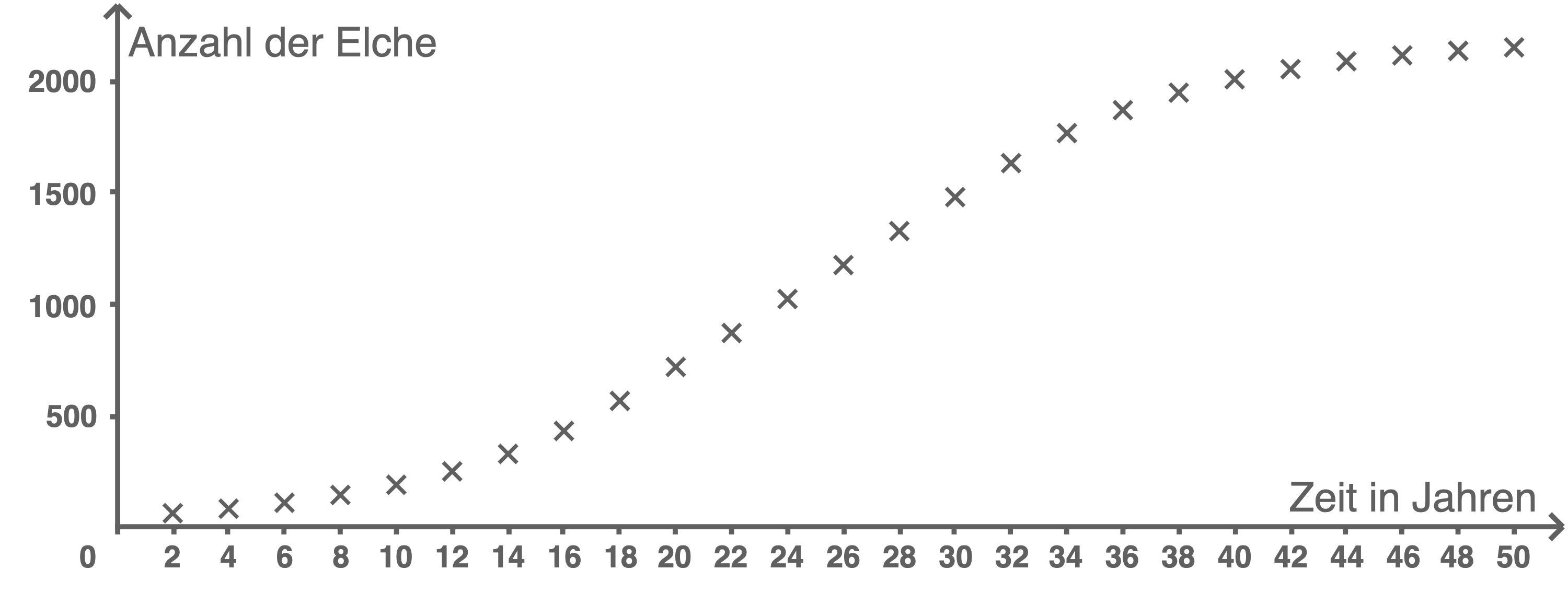
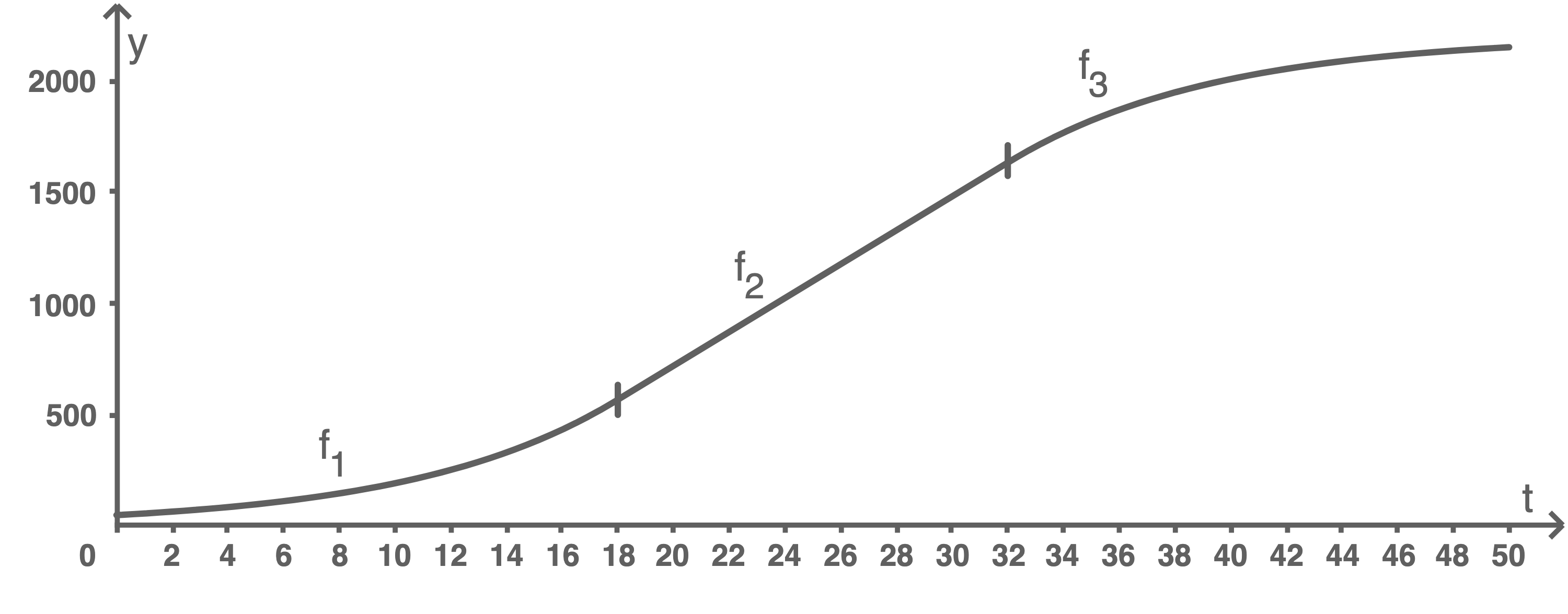

Abbildung 1

Abbildung 2
1.1
Zu Beginn der Untersuchung sind 50 Elche vorhanden, nach 18 Jahren 568 Elche. Die Anzahl der Elche wird in den ersten 18 Jahren durch eine Exponentialfunktion  mit
mit  modelliert.
Berechne die Parameter
modelliert.
Berechne die Parameter  und
und  Begründe, warum die Funktion
Begründe, warum die Funktion  nicht zur langfristigen Beschreibung der Anzahl der Elche geeignet ist.
nicht zur langfristigen Beschreibung der Anzahl der Elche geeignet ist.
(6 BE)
1.2
Im Intervall  soll die Anzahl der Elche durch eine lineare Funktion
soll die Anzahl der Elche durch eine lineare Funktion  mit
mit  modelliert werden.
Beschreibe die Bedeutung der Steigung
modelliert werden.
Beschreibe die Bedeutung der Steigung  im Sachzusammenhang.
im Sachzusammenhang.
(2 BE)
1.3
Ab dem Zeitpunkt  wird die Funktion
wird die Funktion  mit
mit  zur Modellierung der Anzahl der Elche verwendet.
zur Modellierung der Anzahl der Elche verwendet.
1.3.1
Untersuche das Grenzwertverhalten von  für
für  anhand des Funktionsterms.
anhand des Funktionsterms.
(3 BE)
1.3.2
Berechne mit Hilfe der Funktion  den Zeitpunkt, ab dem die Wachstumsrate höchstens 10 Elche pro Jahr beträgt.
den Zeitpunkt, ab dem die Wachstumsrate höchstens 10 Elche pro Jahr beträgt.
(5 BE)
1.3.3
Berechne den Wert des Integrals  und deute das Ergebnis im Sachzusammenhang.
und deute das Ergebnis im Sachzusammenhang.
(6 BE)
2
Die Anzahl der Elche soll im Folgenden durch die Funktion  mit
mit  modelliert werden. Hierbei bezeichnet
modelliert werden. Hierbei bezeichnet  die Zeit in Jahren nach Beginn der Untersuchung aus Aufgabe 1,
die Zeit in Jahren nach Beginn der Untersuchung aus Aufgabe 1,  die Anzahl der Elche. Der Graph von
die Anzahl der Elche. Der Graph von  ist in Abbildung 3 dargestellt.
Für den Zusammenhang zwischen der Funktion
ist in Abbildung 3 dargestellt.
Für den Zusammenhang zwischen der Funktion  und der Ableitungsfunktion
und der Ableitungsfunktion  gilt
gilt  wobei
wobei  eine positive Konstante ist.
eine positive Konstante ist.
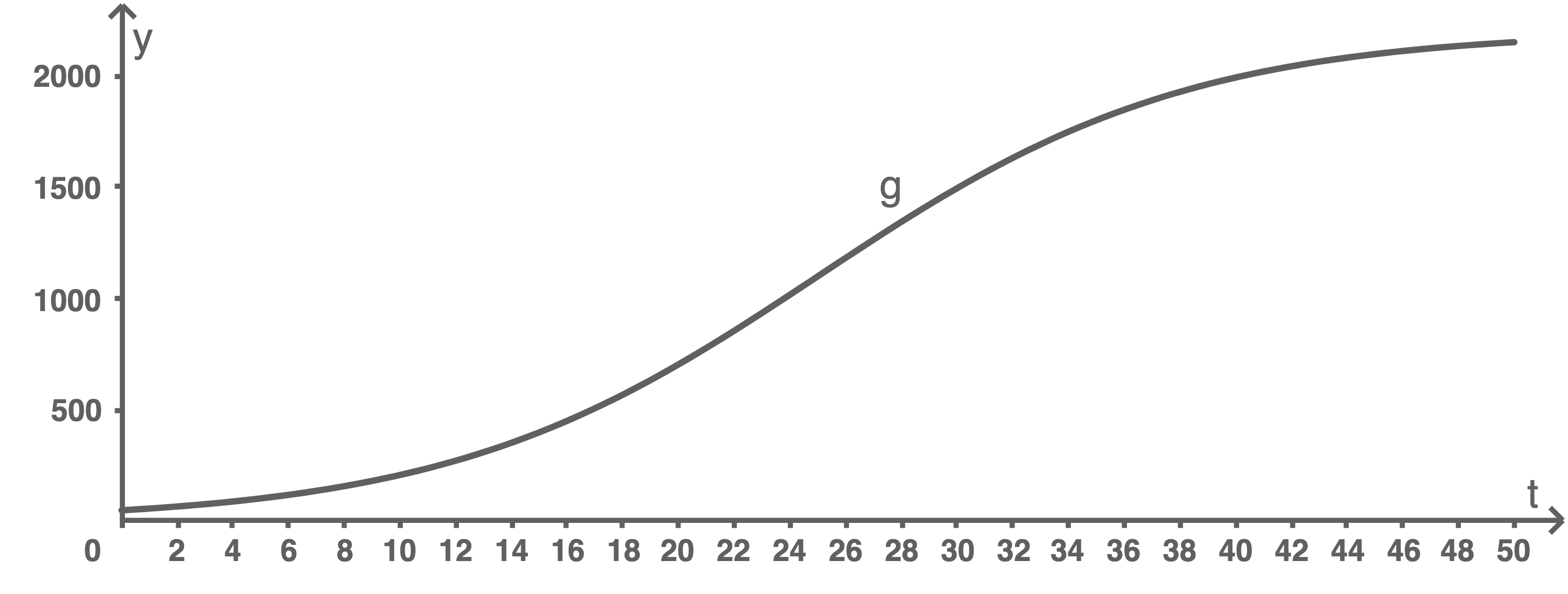
Abbildung 3
2.1
Zeige mit Hilfe der Produktregel, dass  gilt.
gilt.
(3 BE)
2.2
Bestätige unter Bezugnahme auf die Gleichung aus Aufgabe 2.1 nur unter Verwendung der notwendigen Bedingung, dass für die  -Koordinate
-Koordinate  ein Wendepunkt des Graphen von
ein Wendepunkt des Graphen von  vorliegt, und berechne den zugehörigen Zeitpunkt
vorliegt, und berechne den zugehörigen Zeitpunkt  Beschreibe die Bedeutung von
Beschreibe die Bedeutung von  im Sachzusammenhang.
im Sachzusammenhang.
(8 BE)
2.3
Für alle  gilt
gilt  Gib an, welche Symmetrieeigenschaft des Graphen von
Gib an, welche Symmetrieeigenschaft des Graphen von  man aus dieser Gleichung folgern kann.
man aus dieser Gleichung folgern kann.
(2 BE)
3
50 Jahre nach Beginn der Untersuchung aus Aufgabe 1 ist in einem strengen Winter das Wasser zwischen Festland und Insel teilweise zugefroren, sodass 23 Wölfe auf die Insel gelangen.
Die Anzahl der Elche bzw. Wölfe lässt sich in guter Näherung durch die Funktionen  bzw.
bzw.  modellieren mit:
modellieren mit:

 Hierbei bezeichnet
Hierbei bezeichnet  mit
mit  die Zeit in Jahren nach Beginn der Untersuchung,
die Zeit in Jahren nach Beginn der Untersuchung,  bzw.
bzw.  die Anzahl der Elche bzw. Wölfe.
die Anzahl der Elche bzw. Wölfe.
3.1
Beschreibe, durch welche geometrischen Operationen der Graph von  aus dem Graphen der allgemeinen Sinusfunktion
aus dem Graphen der allgemeinen Sinusfunktion  mit
mit  hervorgeht.
Ermittle die Periodenlänge von
hervorgeht.
Ermittle die Periodenlänge von  sowie die maximale und minimale Anzahl der Wölfe.
sowie die maximale und minimale Anzahl der Wölfe.
(6 BE)
3.2
Zeige, dass die zweite Ableitungsfunktion  und die erste Ableitungsfunktion
und die erste Ableitungsfunktion  proportional zueinander sind, dass also gilt
proportional zueinander sind, dass also gilt  , und berechne die Proportionalitätskonstante
, und berechne die Proportionalitätskonstante 
(5 BE)
3.3
Begründe, dass sich an den Stellen, an denen ein Hochpunkt von  vorliegt, auch ein Hochpunkt von
vorliegt, auch ein Hochpunkt von  befindet.
Deute diese Aussage im Sachzusammenhang.
befindet.
Deute diese Aussage im Sachzusammenhang.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Parameter berechnen
Gegeben sind die Koordinaten der beiden Punkte  und
und  Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_1(0)&=& 50& \\[5pt]
a\cdot \mathrm e^{k\cdot 0}&=& 50& \\[5pt]
a&=& 50
\end{array}\)](https://mathjax.schullv.de/5a8fa2e97a3085e77c43f523458911d3768cd27ab07fadf03ee85faf1cc3abd8?color=5a5a5a) Mit den Koordinaten von
Mit den Koordinaten von  folgt:
folgt:
![\(\begin{array}[t]{rll}
f_1(18)&=& 568 & \\[5pt]
50\cdot \mathrm e^{k\cdot 18}&=& 568 &\quad \scriptsize \mid\; :50\\[5pt]
\mathrm e^{k\cdot 18}&=& \dfrac{568}{50} &\quad \scriptsize \mid\; \ln \\[5pt]
18k&\approx& 2,43 &\quad \scriptsize \mid\; :18\\[5pt]
k&\approx& 0,135
\end{array}\)](https://mathjax.schullv.de/a8cbede5cf760d77d5d38376c710b95ab197929c580d075f620abab1610e1971?color=5a5a5a) Begründung
Die Exponentialfunktion strebt mit zunehmenden Werten von
Begründung
Die Exponentialfunktion strebt mit zunehmenden Werten von  gegen Unendlich. Ein solch enormes und rasch steigendes Wachstum kann durch verschiedene Umweltfaktoren nicht auftreten, da der Lebensraum, die Lebenszeit sowie die Nahrungsquellen der Elche begrenzt sind.
gegen Unendlich. Ein solch enormes und rasch steigendes Wachstum kann durch verschiedene Umweltfaktoren nicht auftreten, da der Lebensraum, die Lebenszeit sowie die Nahrungsquellen der Elche begrenzt sind.
1.2
Die Steigung  bedeutet, dass die Anzahl der Elche jedes Jahr um 76 Elche zunimmt.
bedeutet, dass die Anzahl der Elche jedes Jahr um 76 Elche zunimmt.
1.3.1
Für  verläuft
verläuft  Somit folgt für den gesamten Funktionsterm:
Somit folgt für den gesamten Funktionsterm:
![\(\begin{array}[t]{rll}
\lim\limits_{t\to+\infty}f_3(t)&=& 2200-50\cdot 0 & \\[5pt]
&=& 2200
\end{array}\)](https://mathjax.schullv.de/960f777d8747398ff1553940c6960d9746f4e5804c21b99ef659785e77f07458?color=5a5a5a)
1.3.2
Kettenregel anwenden:
 Der Zeitpunkt ab dem die Wachstumsrate höchstens 10 Elche pro Jahr beträgt, ergibt sich aus:
Mit Hilfe der Abbildung 2 folgt, dass die Wachstumsrate etwa ab dem 47. Jahr höchstens 10 Elche pro Jahr beträgt.
Der Zeitpunkt ab dem die Wachstumsrate höchstens 10 Elche pro Jahr beträgt, ergibt sich aus:
Mit Hilfe der Abbildung 2 folgt, dass die Wachstumsrate etwa ab dem 47. Jahr höchstens 10 Elche pro Jahr beträgt.
1.3.3
Mit dem WTR ergibt sich:
 In den Jahren 32 bis 50 nach Beginn der Untersuchung beträgt die Anzahl der Elche durchschnittlich 1987.
In den Jahren 32 bis 50 nach Beginn der Untersuchung beträgt die Anzahl der Elche durchschnittlich 1987.
2.1
Mit der Produktregel ergibt sich:
2.2
2.3
Aus der Gleichung kann die Punktsymmetrie des Graphen zum Punkt  gefolgert werden.
gefolgert werden.
3.1
Geometrische Operationen beschreiben
Der Faktor 10 streckt den Graphen der Sinusfunktion in  -Richtung und vergrößert somit die Amplitude um das 10-fache.
Der Faktor
-Richtung und vergrößert somit die Amplitude um das 10-fache.
Der Faktor  streckt den Graphen der Sinusfunktion in
streckt den Graphen der Sinusfunktion in  -Richtung und vergrößert somit die Periodenlänge.
Durch Addition von 23 wird der Graph der Sinusfunktion um 23 Einheiten in positive
-Richtung und vergrößert somit die Periodenlänge.
Durch Addition von 23 wird der Graph der Sinusfunktion um 23 Einheiten in positive  -Richtung verschoben.
Periodenlänge berechnen
Es gilt:
-Richtung verschoben.
Periodenlänge berechnen
Es gilt:
![\(\begin{array}[t]{rll}
b&=& 0,08\cdot \pi&\\[5pt]
\dfrac{2\pi}{p}&=& 0,08\cdot \pi &\quad \scriptsize \mid\; :\pi \\[5pt]
\dfrac{2}{p}&=& 0,08 &\quad \scriptsize \mid\; \cdot p\\[5pt]
2&=& 0,08\cdot p&\quad \scriptsize \mid\; :0,08\\[5pt]
25&\approx& p& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/8a39b0590f475d91abfec0f175685217b0d5462a65690afce7b3cfc396c5ffa3?color=5a5a5a) Die Periodenlänge von
Die Periodenlänge von  beträgt somit 25.
Maximale und minimale Anzahl ermitteln
Da die Sinusfunktion um den Faktor 23 in
beträgt somit 25.
Maximale und minimale Anzahl ermitteln
Da die Sinusfunktion um den Faktor 23 in  -Richtung verschoben ist und die Amplitude 10 besitzt, folgt die maximale Anzahl der Wölfe mit
-Richtung verschoben ist und die Amplitude 10 besitzt, folgt die maximale Anzahl der Wölfe mit  und die minimale Anzahl mit
und die minimale Anzahl mit 
3.2
1. Schritt: Ableitungen bestimmen
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/6ecdd63594bd4abe240607ca0b8410b6f972c6d0053c586a8851334607592a0d?color=5a5a5a) 2. Schritt: Proportionalität nachweisen
Somit sind die zweite Ableitungsfunktion
2. Schritt: Proportionalität nachweisen
Somit sind die zweite Ableitungsfunktion  und die erste Ableitungsfunktion
und die erste Ableitungsfunktion  propotional zueinander mit der Proportionalitätskonstante
propotional zueinander mit der Proportionalitätskonstante 
3.3
Begründung
Für die Stellen, an denen ein Hochpunkt von  vorliegt, gilt
vorliegt, gilt  Da
Da  proportional zu
proportional zu  ist, folgt:
ist, folgt:
![\(\begin{array}[t]{rll}
w](https://mathjax.schullv.de/117f1e09d0db0404c8513d35d81acbd17b576e8718d61e59f54b9ed89984cbff?color=5a5a5a) Dies entspricht der notwendigen Bedingung für eine Extremstelle bei
Dies entspricht der notwendigen Bedingung für eine Extremstelle bei  Aus der Proportionalität von
Aus der Proportionalität von  und
und  folgt auch die Proportionalität von
folgt auch die Proportionalität von  und
und  wodurch ebenso die hinreichende Bedingung erfüllt ist.
Wegen
wodurch ebenso die hinreichende Bedingung erfüllt ist.
Wegen  wird außerdem garantiert, dass sich an den Stellen, an denen sich ein Hochpunkt von
wird außerdem garantiert, dass sich an den Stellen, an denen sich ein Hochpunkt von  befindet, auch ein Hochpunkt und kein Tiefpunkt von
befindet, auch ein Hochpunkt und kein Tiefpunkt von  befindet.
Deutung im Sachzusammenhang
In dem Jahr, in dem die Anzahl der Elche maximal ist, nimmt die Wolfspopulation am stärksten zu.
befindet.
Deutung im Sachzusammenhang
In dem Jahr, in dem die Anzahl der Elche maximal ist, nimmt die Wolfspopulation am stärksten zu.