B1 - Analytische Geometrie

Die beiden quadratischen Hälften eines Beachvolleyballfelds sind jeweils $8\,\text{m}$ lang und breit. Sie werden durch ein Netz voneinander getrennt, dessen obere Kante $2,4\,\text{m}$ über dem horizontalen Sandboden verläuft. Das Netz ist an zwei vertikal stehenden Pfosten befestigt, die $10\,\text{m}$ voneinander entfernt sind. Die beiden Pfosten haben den gleichen Abstand von den seitlichen Begrenzungslinien des Spielfelds.
Für ein Computerspiel werden das Spielfeld, das Netz und eine Stehtribüne vereinfacht, aber maßstabsgetreu in einem kartesischen Koordinatensystem dargestellt (Material). Eine Längeneinheit im Koordinatensystem entspricht $1\,\text{m}$ in der Realität; die $x_1$ - $x_2$ -Ebene beschreibt den Sandboden.

Die Punkte $A,$ $B,$ $C$ und $D$ sind die Eckpunkte des Spielfelds. Die beiden Strecken, die die Pfosten abbilden, enden in den Punkten $E$ und $F(-1 \mid 8 \mid 2,4)$ an der Oberkante des Netzes. Die Tribüne wird durch ein Viereck dargestellt, dessen Eckpunkte $G(-4 \mid 0 \mid 0),$ $H(-4 \mid 16 \mid 0),$ $I(-10 \mid 20 \mid 4)$ und $J(-10 \mid -4\mid 4)$ in der Ebene $L: 2x_1 + 3x_3 = -8$ liegen.

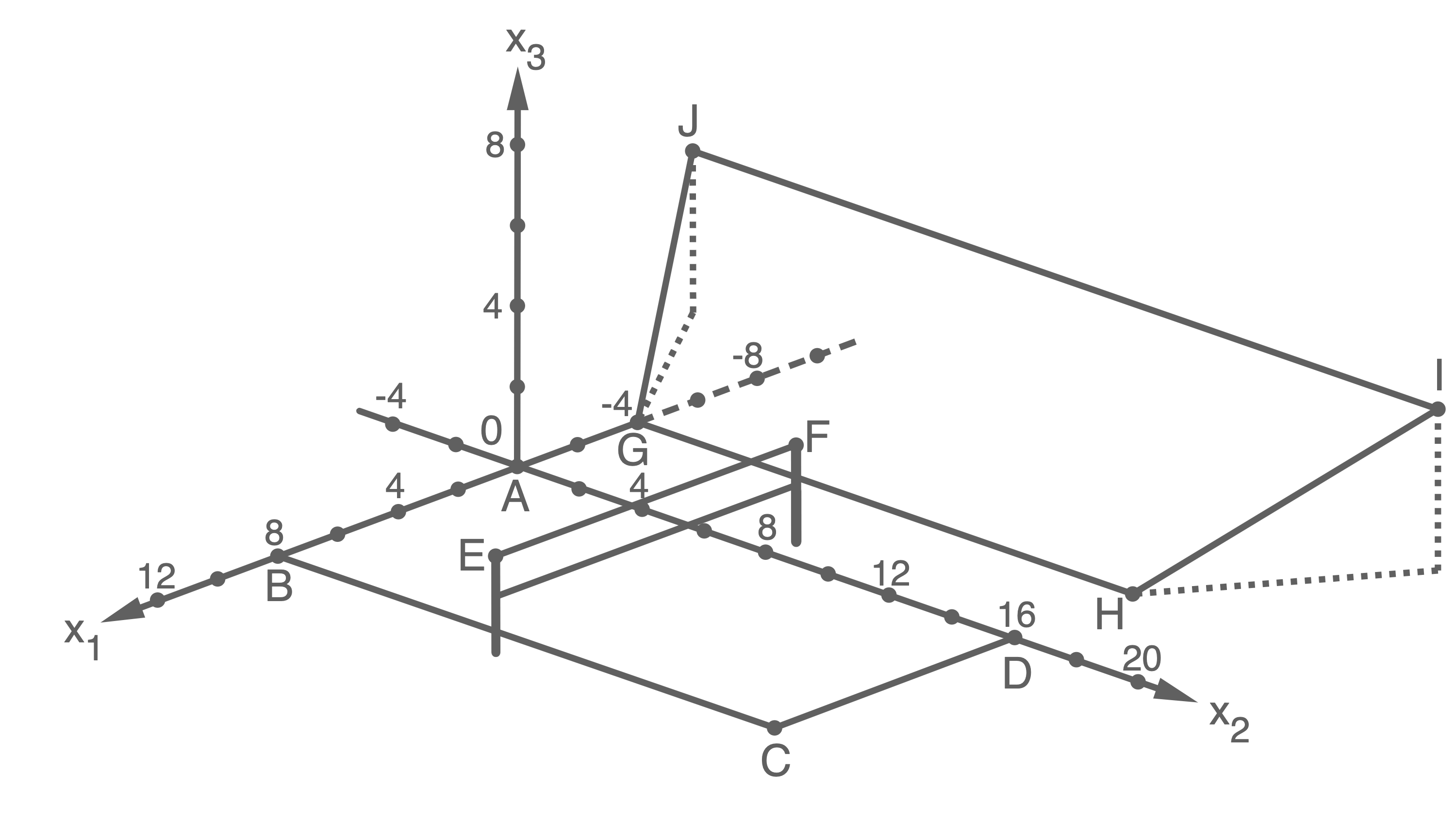
Material

1.1

Zeige, dass die Tribüne die Form eines gleichschenkligen Trapezes hat.

(3 BE)

1.2

Berechne den Neigungswinkel der Tribüne gegenüber der Spielfeldfläche.

(2 BE)

1.3

In der Realität nimmt man an, dass pro Person $0,5\,\text{m}^2$ der Stehtribüne eingenommen werden.
Ermittle die Anzahl der Zuschauer, die im Computerspiel dargestellt werden müssen, um eine voll besetzte Tribüne zu zeigen.

(5 BE)

1.4

Berechne den Abstand des Punkts $F$ von der Ebene $L.$

(3 BE)

1.5

Begründe anhand einer geeigneten Zeichnung, dass kein Punkt des Vierecks, das die Tribüne darstellt, vom Punkt $F$ den gleichen Abstand wie die Ebene $L$ hat.

(4 BE)

Im Folgenden wird der Ball im Modell vereinfachend als punktförmig angenommen. Nach einem Angriffsschlag bewegt sich der Ball vom Punkt $(2 \mid7,5 \mid3)$ aus näherungsweise geradlinig in Richtung des Vektors $\pmatrix{0\\4\\-3}.$
Untersuche rechnerisch, ob der Ball das Netz berührt.

(4 BE)

Ein Aufschlag wird hinter der parallel zum Netz verlaufenden Begrenzungslinie der von der Tribüne aus gesehen rechten Spielfeldhälfte ausgeführt. Anschließend kann die Bahn des Balls mithilfe der Punkte $X_t(3 \mid 12t-1 \mid -5t^2 + 4t + 2,8)$ beschrieben werden; dabei ist $t$ die seit dem Schlag vergangene Zeit in Sekunden. Auf dieser Bahn überfliegt der Ball das Netz.

3.1

Begründe, dass sich der Ball in einer Ebene bewegt, und gib eine Gleichung dieser Ebene an.

(2 BE)

3.2

Untersuche, ob der Ball innerhalb des Spielfelds auf dem Boden auftrifft, wenn er nach dem Aufschlag von keinem Spieler berührt wird.

(4 BE)

Die Bildschirmansicht des Beachvolleyballfelds soll verändert werden. Beabsichtigt ist ein Perspektivwechsel, der eine Drehung um die $x_3$ -Achse um $90^{\circ}$ gegen den Uhrzeigersinn sowie eine Verkleinerung in $x_3$ -Richtung um $30\,\%$ vorsieht.
Gib die zugehörige Matrix an.

(3 BE)

1.1

1. Schritt: Trapezform zeigen

Bei einem Viereck handelt es sich um ein Trapez, wenn zwei gegenüberliegende Seiten parallel sind. Der Abbildung im Material kann entnommen werden, dass mit großer Wahrscheinlichkeit die beiden Strecken $\overline{GH}$ und $\overline{JI}$ parallel sind.

Verbindungsvektoren auf lineare Abhängigkeit überprüfen:

$\begin{array}[t]{rll} \overrightarrow{GH}&=& a\cdot \overrightarrow{JI} \\[5pt] \pmatrix{0\\16\\0}&=& a\cdot \pmatrix{0\\24\\0} \end{array}$

Diese Gleichung ist für $a=\frac{2}{3}$ erfüllt. Die beiden Vektoren $\overrightarrow{GH}$ und $\overrightarrow{JI}$ sind also Vielfache voneinander und somit parallel. Die Tribüne ist demnach trapezförmig.

2. Schritt: Gleichschenkligkeit prüfen

Ein Trapez ist gleichschenklig, wenn es achsensymmetrisch ist. Die Symmetrieachse verläuft dann senkrecht zu den beiden parallelen Seiten durch ihre Mittelpunkte. Das Trapez ist also gleichschenklig, wenn $\overrightarrow{M_1M_2}$ senkrecht zu $\overrightarrow{GH}$ und $\overrightarrow{JI}$ ist.

Mittelpunkte $M_1$ und $M_2$ bestimmen:

$\begin{array}[t]{rll} \overrightarrow{OM_1}&=& \frac{1}{2}\cdot \left(\overrightarrow{OG} +\overrightarrow{OH} \right) \\[5pt] &=& \frac{1}{2}\cdot \left(\pmatrix{-4\\0\\0} +\pmatrix{-4\\16\\0}\right) \\[5pt] &=& \pmatrix{-4\\8\\0} \\[10pt] \overrightarrow{OM_2}&=& \frac{1}{2}\cdot \left(\overrightarrow{OI} +\overrightarrow{OJ} \right) \\[5pt] &=& \frac{1}{2}\cdot \left(\pmatrix{-10\\20\\4} +\pmatrix{-10\\-4\\4}\right) \\[5pt] &=& \pmatrix{-10\\8\\4} \end{array}$

Mit dem Skalarprodukt kann die Orthogonalität überprüft werden:

$\begin{array}[t]{rll} \overrightarrow{GH}\circ \overrightarrow{M_1M_2}&=& \pmatrix{0\\16\\0} \circ \pmatrix{-6\\0\\4} \\[5pt] &=& 0\cdot (-6) +16\cdot 0 +0\cdot 4 \\[5pt] &=& 0 \\[10pt] \overrightarrow{JI}\circ \overrightarrow{M_1M_2}&=& \pmatrix{0\\24\\0} \circ \pmatrix{-6\\0\\4} \\[5pt] &=& 0\cdot (-6) +24\cdot 0 +0\cdot 4 \\[5pt] &=& 0 \\[5pt] \end{array}$

Das Trapez $GHIJ$ besitzt also die Gerade durch die Punkte $M_1$ und $M_2$ als Symmetrieachse und ist damit gleichschenklig. Die Tribüne hat folglich insgesamt die Form eines gleichschenkligen Trapezes.

1.2

Die Spielfeldfläche liegt in der $x_1-x_2$ -Ebene. Ein zugehöriger Normalenvektor ist also $\overrightarrow{n}_1 = \pmatrix{0\\0\\1}.$ Die Tribüne liegt in der Ebene $L:\, 2x_1 +3x_3 = -8,$ ein zugehöriger Normalenvektor ist folglich $\overrightarrow{n}_2 = \pmatrix{2\\0\\3}.$

Einsetzen in die Formel für den Schnittwinkel $\alpha$ zweier Ebenen liefert:

Rechenweg anzeigen

$\alpha \approx 33,7^{\circ}$

Die Tribüne ist gegenüber dem Spielfeld also um ca. $33,7^{\circ}$ geneigt.

1.3

1. Schritt: Flächeninhalt der Tribüne berechnen

Die Höhe des Trapezes $GHIJ$ entspricht aufgrund der Gleichschenklichkeit dem Abstand der beiden Mittelpunkte $M_1$ und $M_2.$ Mit dem Vektorbetrag ergibt sich:

$\begin{array}[t]{rll} h&=& \left| \overrightarrow{M_1M_2}\right| \\[5pt] &=& \left|\pmatrix{-6\\0\\4}\right| \\[5pt] &=& \sqrt{(-6)^2 +0^2 +4^2} \\[5pt] &=& \sqrt{52} \; [\text{m}] \end{array}$

Die Längen der beiden parallelen Seiten des Trapezes können ebenfalls über die Vektorbeträge der zugehörigen Verbindungsvektoren berechnet werden:

$\begin{array}[t]{rll} a &=& \left|\overrightarrow{GH} \right| \\[5pt] &=& \left|\pmatrix{0\\16\\0} \right| \\[5pt] &=& \sqrt{0^2+16^2+0^2} \\[5pt] &=& 16 \; [\text{m}] \\[10pt] c &=& \left|\overrightarrow{JI} \right| \\[5pt] &=& \left|\pmatrix{0\\24\\0} \right| \\[5pt] &=& \sqrt{0^2+24^2+0^2} \\[5pt] &=& 24 \; [\text{m}]\\[10pt] \end{array}$

Einsetzen in die Formel für den Flächeninhalt eines Trapezes liefert:

$\begin{array}[t]{rll} A&=& \frac{1}{2}\cdot \left(a+c\right)\cdot h \\[5pt] &=& \frac{1}{2}\cdot \left(16 +24\right)\cdot \sqrt{52} \\[5pt] &\approx& 144,22 \; [\,\text{m}^2] \\[5pt] \end{array}$

Die Tribüne ist also ca. $144,22\,\text{m}^2$ groß.

2. Schritt: Zuschaueranzahl berechnen

$144,22\,\text{m}^2 : 0,5\,\text{m}^2 \approx 288$

Um eine vollbesetzte Tribüne zu zeigen müssten also 288 Zuschauer dargestellt werden.

1.4

Der Abstand eines Punkts zu einer Ebene kann mithilfe der Hesseschen Normalform berechnet werden.

Durch Umformen der Ebenengleichung und Teilen durch den Betrag des Normalenvektors folgt:

$\begin{array}[t]{rll} L:\quad \dfrac{2x_1 +3x_3-(-8)}{\sqrt{2^2+0^2+3^2}} &=& 0 \\[5pt] \dfrac{2x_1 +3x_3+8}{\sqrt{13}} &=& 0 \end{array}$

Einsetzen der Koordinaten von $F$ liefert:

$\begin{array}[t]{rll} d(F,L)&=& \dfrac{\left|2\cdot (-1) +3\cdot 2,4+8\right|}{\sqrt{13}}& \\[5pt] &\approx& 3,66 \end{array}$

Der Punkt $F$ hat folglich einen Abstand von ca. $3,66\,\text{m}$ zur Ebene $L.$

1.5

Der Abstand zwischen dem Punkt $F$ und der Ebene $L$ entspricht dem Abstand von $F$ zu dem Punkt $P$ innerhalb der Ebene $L$ mit dem kürzesten Abstand zu $F.$ Dies ist der Punkt, in dem die Gerade, die durch den Punkt $F$ orthogonal zur Ebene $L$ verläuft auf die Ebene $L$ trifft.
Dieser Punkt ist eindeutig, es gibt also nur einen solchen Punkt in der gesamten Ebene $L,$ der den gleichen Abstand zu $F$ besitzt wie die gesamte Ebene $L.$
Dieser Punkt $P$ liegt im betrachteten Fall außerhalb des Vierecks $GHIJ,$ wie sich in der folgenden Abbildung erkennen lässt.

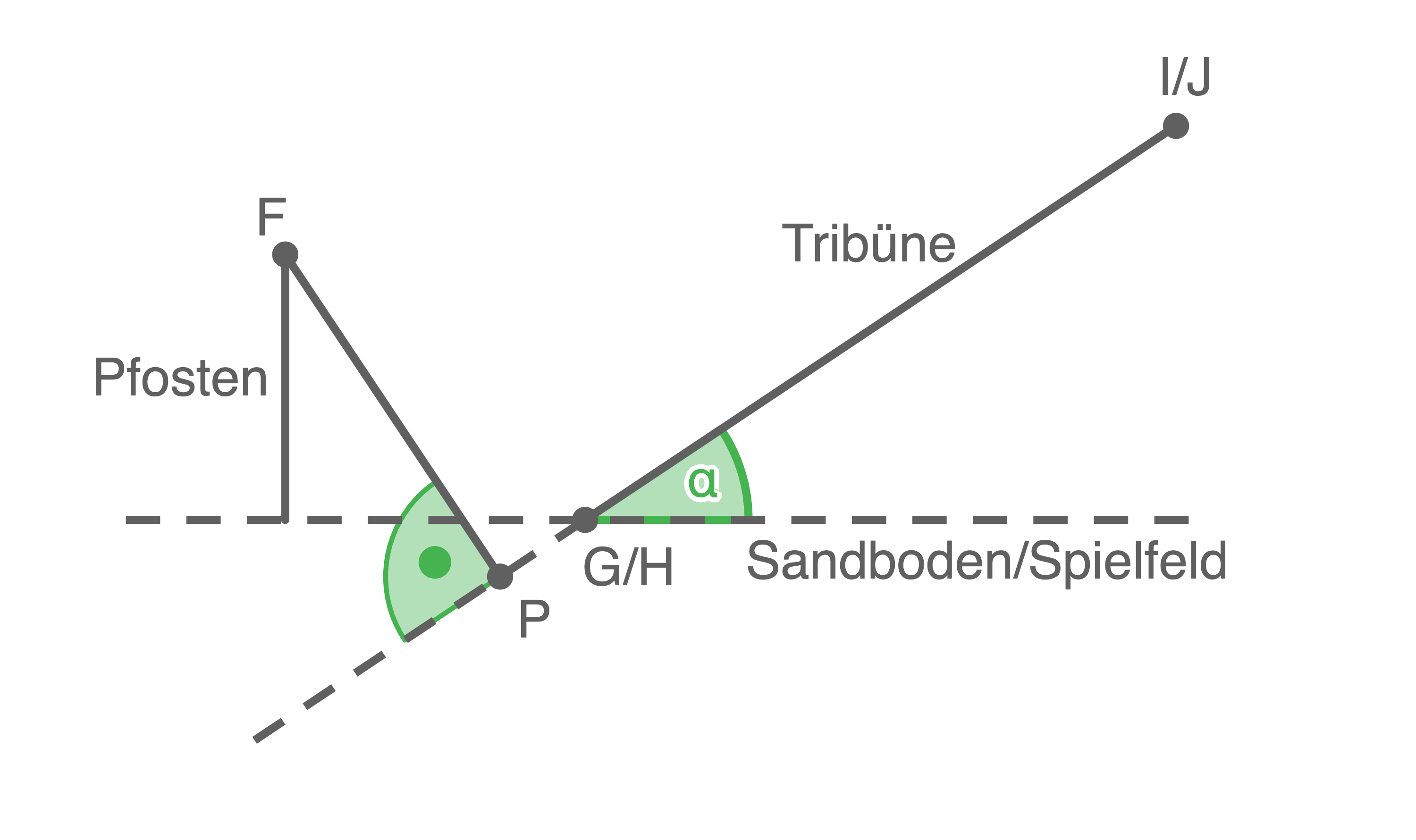
Hilfsskizze Neigungswinkel Tribüne Hessen Abi 2018

Querschnitt auf die Tribüne und den Pfosten, frontaler Blick auf die $x_1x_3$ -Ebene

Die Flugbahn des Balls kann näherungsweise durch folgende Gerade beschrieben werden:

$g: \, \overrightarrow{x} = \pmatrix{2\\7,5\\3} + s\cdot \pmatrix{0\\4\\-3}$

Das Netz liegt parallel zur $x_1x_3$ -Ebene. Alle Punkte auf dem Netz haben daher dieselbe $x_2$ -Koordinate wie $F,$ es gilt also $x_2 = 8.$

Durch Gleichsetzen mit der entsprechenden Zeile der Geradengleichung von $g$ folgt:

$\begin{array}[t]{rll} 8&=& 7,5+s\cdot 4&\quad \scriptsize \mid\;-7,5 \\[5pt] 0,5&=& s\cdot 4&\quad \scriptsize \mid\; :4 \\[5pt] 0,125 &=& s \end{array}$

Einsetzen in die Geradengleichung liefert:

Rechnung anzeigen 

Zum Zeitpunkt, an dem sich der Ball in der Ebene des Netzes befindet, fliegt er in einer Höhe von $2,625\,\text{m}.$ Die Oberkante des Netzes befindet sich aufgrund der $x_3$ -Koordinate von $F$ allerdings in einer Höhe von lediglich $2,4\,\text{m}.$ Der Ball berührt das Netz also nicht, sondern fliegt darüber hinweg.

3.1

Da die $x_1$ -Koordinate der Punkte $X_t$ unabhängig vom Parameter $t$ und damit konstant $3$ ist, liegen alle Punkte $X_t$ in der Ebene mit der Gleichung $x_1 =3.$
Der Ball bewegt sich also in der Ebene mit der Gleichung $x_1=3.$

3.2

Da das Spielfeld innerhalb der $x_1x_2$ -Ebene liegt, muss der Schnittpunkt der Flugbahn des Balls mit der $x_1x_2$ -Ebene berechnet werden und anschließend überprüft werden, ob dieser Punkt innerhalb des Spielfelds liegt.

Damit der Ball auf die $x_1x_2$ -Ebene trifft, muss die $x_3$ -Koordinate von $X_t$ null sein.

Gleichsetzen liefert:

Da $t_1$ negativ ist, ist die einzige im Sachzusammenhang sinnvolle Lösung $t_2\approx 1,25.$

Durch Einsetzen von $t$ in $X_t$ ergibt sich:

$X_{1,25}(3\mid 14\mid 0)$

Da das Beachvolleyballfeld insgesamt $8\,\text{m}$ breit und $16\,\text{m}$ lang ist, trifft der Ball damit auf dem Boden innerhalb des Spielfelds auf.

Eine Drehung um die $x_3$ -Achse mit einem Winkel von $\alpha=90^{\circ}$ entgegen dem Uhrzeigersinn kann mit folgender Drehmatrix beschrieben werden:

Rechenweg anzeigen

$D=\pmatrix{0 & -1 & 0 \\ 1 & 0 & 0 \\ 0& 0& 1}$

Eine Verkleinerung um $30\,\%$ entspricht einer Skalierung auf $70\,\%,$ also um den Faktor $0,7.$ Diese kann mit folgender Skalierungsmatrix dargestellt werden:

$S = \pmatrix{1& 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0,7 }$

Insgesamt ergibt sich dadurch folgende Transformationsmatrix:

Rechenweg anzeigen

$T=\pmatrix{0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0,7}$

Bildnachweise [nach oben]

[1]