A2 - Analysis
1.
Ein Wachstumsprozess kann für  durch die Funktion
durch die Funktion  mit
mit  für
für  durch die Funktion
durch die Funktion  mit
mit  beschrieben werden. In der Tabelle (Material 1) sind die Werte des Wachstumsprozesses zu verschiedenen Zeitpunkten
beschrieben werden. In der Tabelle (Material 1) sind die Werte des Wachstumsprozesses zu verschiedenen Zeitpunkten  dargestellt.
dargestellt.
1.1
Bestimme durch Regression die Gleichung der Funktion  Gib dabei die Koeffizienten
Gib dabei die Koeffizienten  und
und  der Funktionsgleichung auf drei Nachkommastellen gerundet an.
der Funktionsgleichung auf drei Nachkommastellen gerundet an.
(3 BE)
1.2
Im Material 2 sind der Graph der Funktion  für
für  und der Graph der Funktion
und der Graph der Funktion  für
für  dargestellt. Untersuche unter Verwendung der auf drei Nachkommastellen gerundeten Ergebnisse, ob die Graphen der Funktionen
dargestellt. Untersuche unter Verwendung der auf drei Nachkommastellen gerundeten Ergebnisse, ob die Graphen der Funktionen  und
und  an der Stelle
an der Stelle  ohne Sprung und ohne Knick ineinander übergehen.
ohne Sprung und ohne Knick ineinander übergehen.
Falls du in Aufgabe 1.1 die Funktion nicht bestimmen konntest, verwende die Ersatzfunktion
nicht bestimmen konntest, verwende die Ersatzfunktion  mit
mit 
Falls du in Aufgabe 1.1 die Funktion
(4 BE)
2.
Der Wachstumsprozess kann für  auch durch eine logistische Wachstumsfunktion
auch durch eine logistische Wachstumsfunktion  mit
mit
 beschrieben werden.
beschrieben werden.
2.1
Bestimme den Zeitpunkt  zu dem die Funktion
zu dem die Funktion 
 ihrer Sättigungsgrenze erreicht hat.
ihrer Sättigungsgrenze erreicht hat.
(4 BE)
2.2
Bestimme innerhalb des Definitionsbereichs den Zeitpunkt  zu dem die Wachstumsgeschwindigkeit am größten ist.
zu dem die Wachstumsgeschwindigkeit am größten ist.
(4 BE)
2.3
Zeige durch eine Rechnung, dass die Funktion  mit
eine Stammfunktion von
mit
eine Stammfunktion von  ist.
ist.
(5 BE)
2.4
Bestimme den Wert des Terms
 und erläutere die mathematische Bedeutung dieses Werts.
und erläutere die mathematische Bedeutung dieses Werts.
(4 BE)
3.
Es wird nun ein weiterer Wachstumsprozess, dessen Wachstumsgeschwindigkeit durch die Funktion  mit
mit  beschrieben wird, betrachtet. Der Wert der zugrunde liegenden Wachstumsfunktion an der Stelle
beschrieben wird, betrachtet. Der Wert der zugrunde liegenden Wachstumsfunktion an der Stelle  soll
soll  betragen.
betragen.
Bestätige durch eine Rechnung, dass der Funktionsterm die dem Wachstumsprozess zugrunde liegende Funktion
die dem Wachstumsprozess zugrunde liegende Funktion  in Abhängigkeit von
in Abhängigkeit von  beschreibt.
beschreibt.
Bestätige durch eine Rechnung, dass der Funktionsterm
(3 BE)
4.1
Skizziere die Graphen der Wachstumsgeschwindigkeiten der beiden Wachstumsprozesse  und
und  aus Aufgabe 2 bzw. 3 in das Koordinatensystem (Material 3). Vergleiche die Wachstumsgeschwindigkeiten der Funktionen
aus Aufgabe 2 bzw. 3 in das Koordinatensystem (Material 3). Vergleiche die Wachstumsgeschwindigkeiten der Funktionen  und
und  für
für 
Begründe ohne Rechnung und unter Verwendung der Skizze, dass bis zur Schnittstelle der Graphen bei die Funktionswerte von
die Funktionswerte von  größer als die Funktionswerte von
größer als die Funktionswerte von  sind.
sind.
Begründe ohne Rechnung und unter Verwendung der Skizze, dass bis zur Schnittstelle der Graphen bei
(7 BE)
4.2
Untersuche, zu welchem Zeitpunkt  die Differenz der Funktionswerte der beiden Wachstumsfunktionen
die Differenz der Funktionswerte der beiden Wachstumsfunktionen  und
und  dem Betrag nach am größten ist.
dem Betrag nach am größten ist.
Hinweis: Auf die Überprüfung der Randwerte kann verzichtet werden.
Material 1
Hinweis: Auf die Überprüfung der Randwerte kann verzichtet werden.
(6 BE)
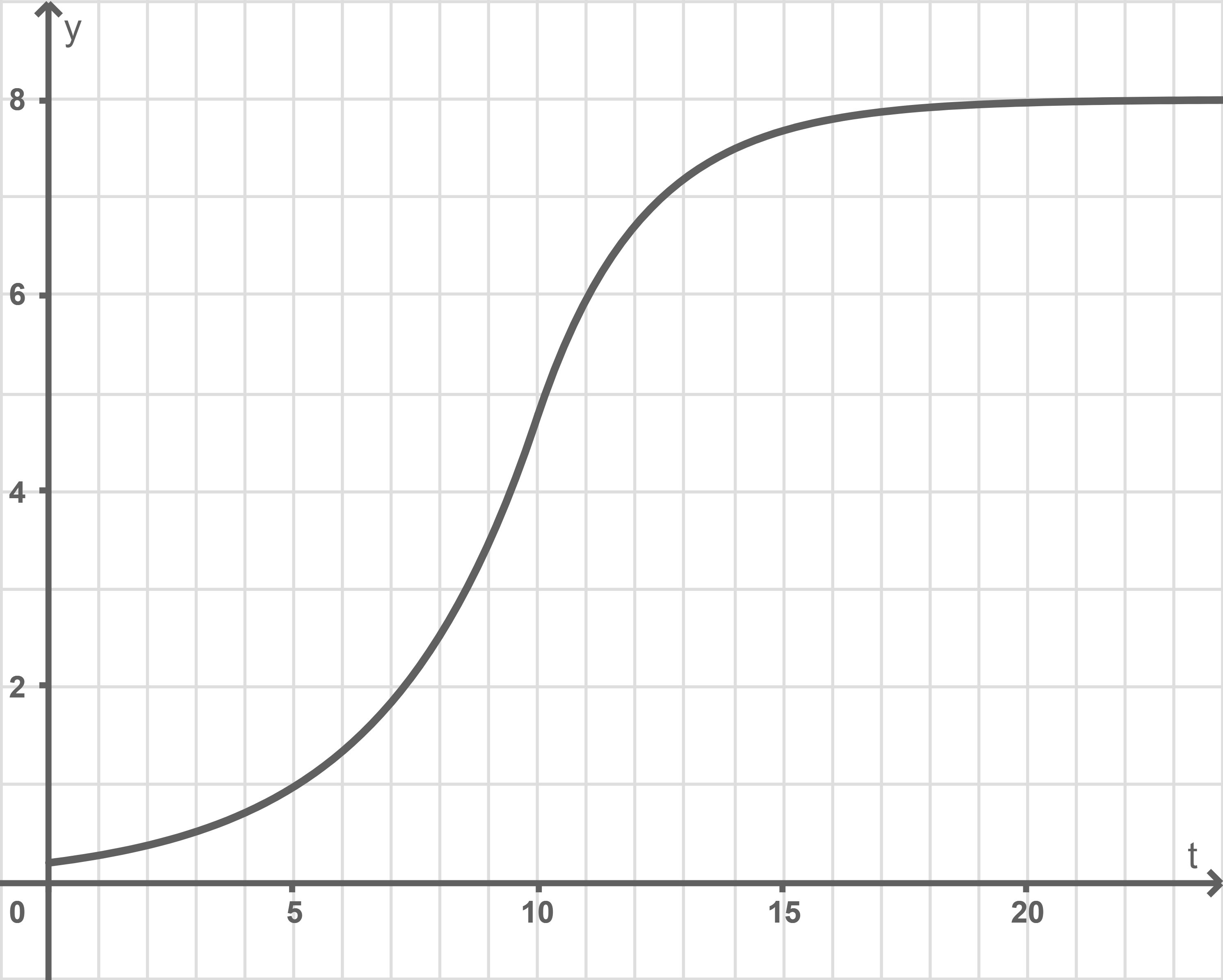
Abb. 1
Abb. 2
1.1
Koeffizienten durch Regression bestimmen
 Abb. 1: Ergebnisse des CAS
Durch Regression ergibt sich mit Hilfe des CAS
Abb. 1: Ergebnisse des CAS
Durch Regression ergibt sich mit Hilfe des CAS 
Eingabe der Wertepaare aus der Tablle im CAS für  unter:
Calc
unter:
Calc  Regressionen
Regressionen  Freie Exp. Reg.
Es folgt:
Freie Exp. Reg.
Es folgt:
 und
und 
 Abb. 1: Ergebnisse des CAS
Abb. 1: Ergebnisse des CAS
1.2
Übergang untersuchen
 Abb. 2: Berechnung der Funktionswerte
Auf drei Nachkommastellen gerundet ergibt sich, dass die beiden Graphen mit einem leichten Sprung (Abweichung von
Abb. 2: Berechnung der Funktionswerte
Auf drei Nachkommastellen gerundet ergibt sich, dass die beiden Graphen mit einem leichten Sprung (Abweichung von  ) und nicht knickfrei ineinander übergehen.
) und nicht knickfrei ineinander übergehen.
Definition der beiden Funktionen  und
und  und der zugehörigen Ableitungsfunktionen mit Hilfe des CAS und Einsetzen von
und der zugehörigen Ableitungsfunktionen mit Hilfe des CAS und Einsetzen von  liefert:
liefert:
 Abb. 2: Berechnung der Funktionswerte
Abb. 2: Berechnung der Funktionswerte
2.1
Zeitpunkt bestimmen
Aus der Funktionsgleichung ergibt sich die Sättigungsgrenze  Davon sollen
Davon sollen  erreicht werden:
erreicht werden:
 Gleichsetzen von
Gleichsetzen von  und Lösen der Gleichung mit dem solve-Befehl des CAS liefert:
und Lösen der Gleichung mit dem solve-Befehl des CAS liefert:
![\(\begin{array}[t]{rll}
h(t)&=& 7,6 \\[5pt]
t&\approx& 15,1
\end{array}\)](https://mathjax.schullv.de/b3f82710bab8fc677b0d1288313386b52dc3da498103f6ff8215dc5917d3c299?color=5a5a5a)
 Abb. 3: Lösen mit dem CAS
Die Funktion erreicht ihre Sättigungsgrenze zu
Abb. 3: Lösen mit dem CAS
Die Funktion erreicht ihre Sättigungsgrenze zu  zum Zeitpunkt
zum Zeitpunkt 
 Abb. 3: Lösen mit dem CAS
Abb. 3: Lösen mit dem CAS
2.2
Zeitpunkt mit größter Wachstumsgeschwindigkeit bestimmen
 Abb. 4: Berechnung mit dem CAS
Da die Funktion
Abb. 4: Berechnung mit dem CAS
Da die Funktion  laut der Überprüfung des notwendigen Kriteriums nur eine Extremstelle besitzt, folgt, dass die Wachstumsgeschwindigkeit zum Zeitpunkt
laut der Überprüfung des notwendigen Kriteriums nur eine Extremstelle besitzt, folgt, dass die Wachstumsgeschwindigkeit zum Zeitpunkt  am größten ist.
am größten ist.
Durch Definition der beiden Ableitungen im CAS und Überprüfen des notwendigen Kriteriums für Extremstellen folgt:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/a0d3f6550a1de96df75dc606e775a8107185260287425681925867a0a9c0b9ac?color=5a5a5a) Einsetzen der dritten Ableitung und Überprüfen des hinreichenden Kriteriums für Extremstellen liefert:
Einsetzen der dritten Ableitung und Überprüfen des hinreichenden Kriteriums für Extremstellen liefert:
 Abb. 4: Berechnung mit dem CAS
Abb. 4: Berechnung mit dem CAS
2.3
Stammfunktion nachweisen
Anwenden der Kettenregel:
Somit ist  eine Stammfunktion von
eine Stammfunktion von 
2.4
Wert bestimmen und erläutern
Der Befehl für das Integral befindet sich unter:
 Abb. 5: Berechnung mit dem CAS
Der Wert beschreibt den durchschnittlichen Funktionswert von
Abb. 5: Berechnung mit dem CAS
Der Wert beschreibt den durchschnittlichen Funktionswert von  im Intervall
im Intervall ![\([0;20].\)](https://mathjax.schullv.de/a7c4269a4f40e3f6312df70e68dfdef51c9217da2efe9b91ae648375e55dc788?color=5a5a5a)
Keyboard  Math2
Somit folgt mit Hilfe des CAS:
Math2
Somit folgt mit Hilfe des CAS:

 Abb. 5: Berechnung mit dem CAS
Abb. 5: Berechnung mit dem CAS
3.
Funktionsterm nachweisen
Berechnung der Ableitung von  liefert:
liefert:

 Einsetzen von
Einsetzen von  in
in  liefert zudem:
Es gilt
liefert zudem:
Es gilt  und
und  Damit beschreibt
Damit beschreibt  die dem Wachstumsprozess zugrunde liegende Funktion
die dem Wachstumsprozess zugrunde liegende Funktion  in Abhängigkeit von der Zeit
in Abhängigkeit von der Zeit 
4.1
Graphen zeichnen
Betrachtung der Graphen von  und
und  und anzeigen der Funktionswerte im CAS liefert:
und anzeigen der Funktionswerte im CAS liefert:
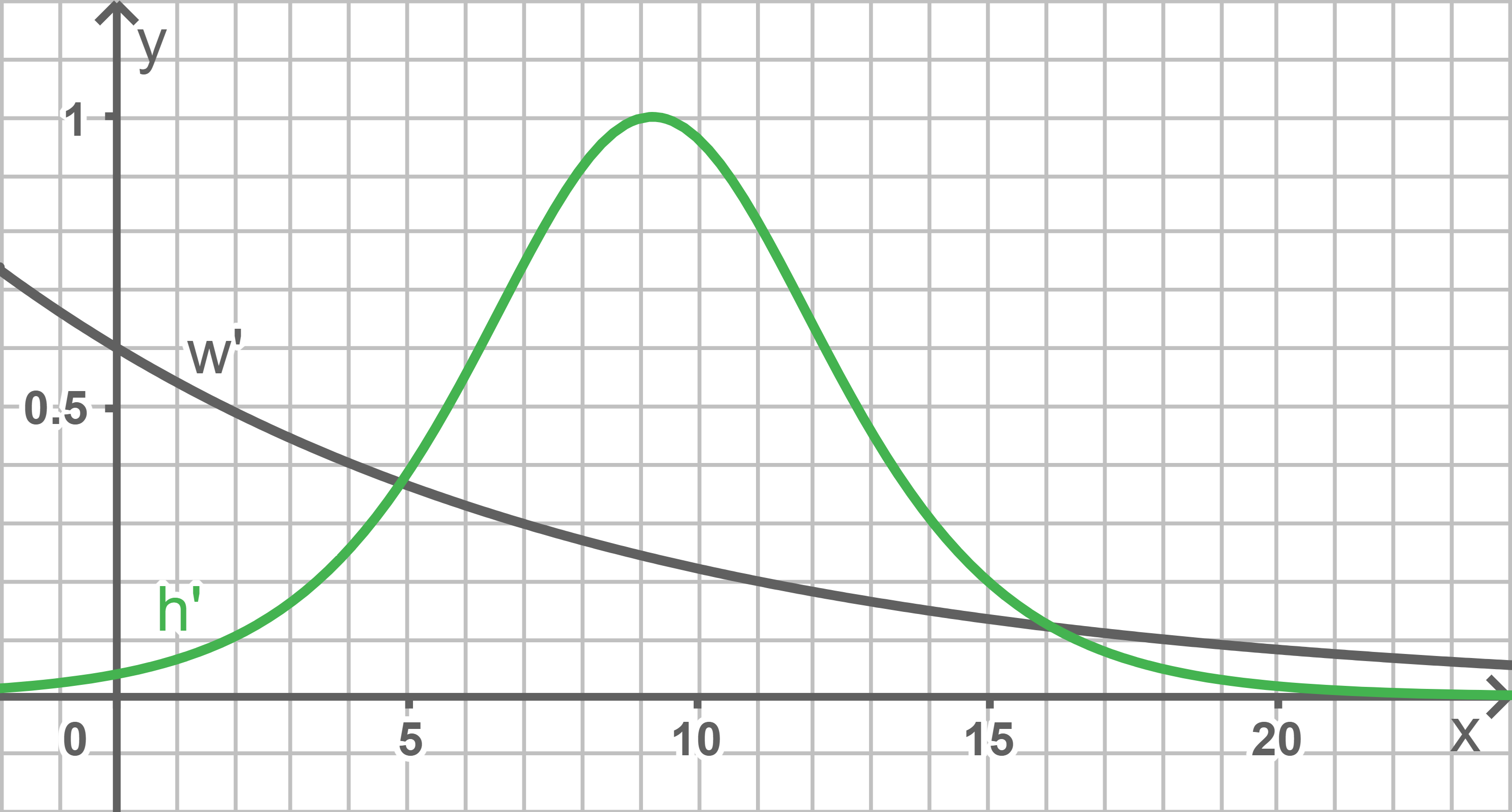 Wachstumsgeschwindigkeiten vergleichen
Zu Beginn ist die Wachstumsgeschwindigkeit von
Wachstumsgeschwindigkeiten vergleichen
Zu Beginn ist die Wachstumsgeschwindigkeit von  mit ca.
mit ca.  deutlich höher als die von
deutlich höher als die von  mit ca.
mit ca.  Die Wachstumsgeschwindigkeit von
Die Wachstumsgeschwindigkeit von  nimmt über den gesamten Zeitraum ab, während die Wachstumsgeschwindigkeit von
nimmt über den gesamten Zeitraum ab, während die Wachstumsgeschwindigkeit von  zunächst stark ansteigt bis sie ihr Maximum bei
zunächst stark ansteigt bis sie ihr Maximum bei  erreicht, und fällt dann in etwa so schnell, wie sie zuvor gestiegen ist, wieder ab. Dabei nähert sich die Wachstumsgeschwindigkeit von
erreicht, und fällt dann in etwa so schnell, wie sie zuvor gestiegen ist, wieder ab. Dabei nähert sich die Wachstumsgeschwindigkeit von  dem Wert Null schneller an.
Verhältnis der Funktionswerte begründen
dem Wert Null schneller an.
Verhältnis der Funktionswerte begründen
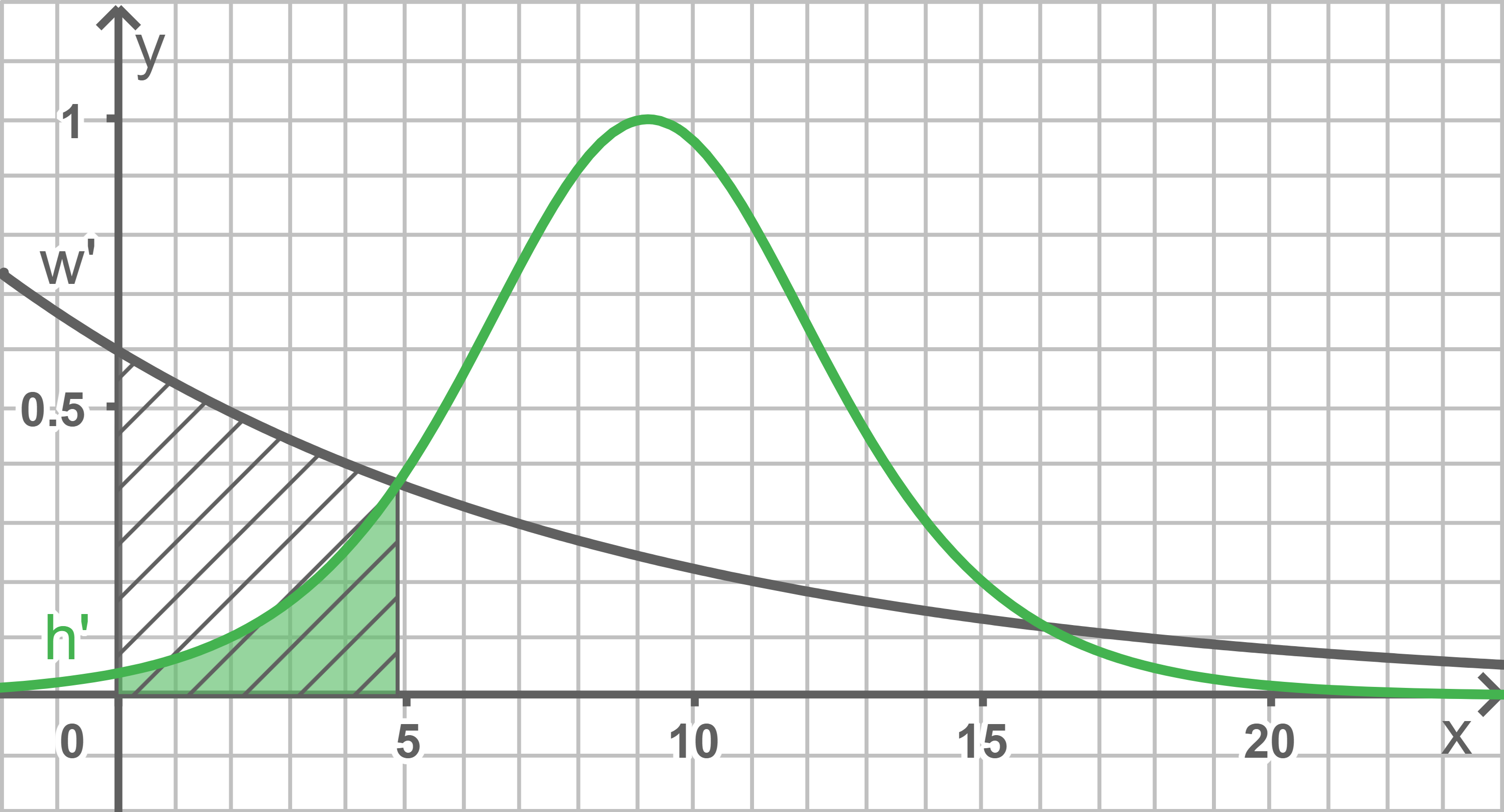 Da
Da  eine Stammfunktion von
eine Stammfunktion von  und
und  eine Stammfunktion von
eine Stammfunktion von  ist, kann der jeweilige Flächeninhalt, der in der Skizze markiert ist, über die Differenz
ist, kann der jeweilige Flächeninhalt, der in der Skizze markiert ist, über die Differenz  bzw.
bzw.  berechnet werden.
Der Flächeninhalt der mit den Achsen eingeschlossenen Fläche im Bereich
berechnet werden.
Der Flächeninhalt der mit den Achsen eingeschlossenen Fläche im Bereich ![\([0;t]\)](https://mathjax.schullv.de/44bd19c8d46989227acb5541af2f57f3aeeebafc33e9b850dd8e6e31071537c1?color=5a5a5a) ist hier bei
ist hier bei  kleiner als bei
kleiner als bei  Da dieser maßgeblich den Funktionswert von
Da dieser maßgeblich den Funktionswert von  bzw.
bzw.  definiert, folgt, dass der Funktionswert von
definiert, folgt, dass der Funktionswert von  bis
bis  kleiner als der von
kleiner als der von  ist.
ist.

Abb. 6: Graphen von  und
und 

Abb. 7: Skizze
4.2
Zeitpunkt mit maximaler Differenz bestimmen
Definition von  und der ersten beiden Ableitungsfunktionen von
und der ersten beiden Ableitungsfunktionen von  in dem CAS und anschließendes Anwenden des notwendigen und hinreichenden Kriteriums für Extremstellen liefert mit dem solve-Befehl des CAS:
in dem CAS und anschließendes Anwenden des notwendigen und hinreichenden Kriteriums für Extremstellen liefert mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
d](https://mathjax.schullv.de/afdb86fceeffb47d54e5d36dae3faaa6213be7400224c0b2f7063be745dd2d3f?color=5a5a5a)
![\(\begin{array}[t]{rll}
d](https://mathjax.schullv.de/c610b450ff3713654b833d3f700e5e30db6176ecd27784a1ee0299270e3fcce9?color=5a5a5a) Die zugehörigen Beträge der Funktionswerte lauten:
Die zugehörigen Beträge der Funktionswerte lauten:
![\(\begin{array}[t]{rll}
\left| d(4,87)\right|&\approx& 3,49 \\[5pt]
\left|d(16,10)\right|&\approx& 0,9
\end{array}\)](https://mathjax.schullv.de/c63e692d1bf2c769a1b096412655d90c5f58f5b196d094108e02df7a822f5bbd?color=5a5a5a)
 Abb. 8: Bestimmung der Extrema mit dem CAS
Zum Zeitpunkt
Abb. 8: Bestimmung der Extrema mit dem CAS
Zum Zeitpunkt  ist die Differenz der Funktionswerte von
ist die Differenz der Funktionswerte von  und
und  demnach dem Betrag nach am größten.
demnach dem Betrag nach am größten.
 Abb. 8: Bestimmung der Extrema mit dem CAS
Abb. 8: Bestimmung der Extrema mit dem CAS