B1 - Analysis

Ein Schnellzug der Deutschen Bahn vom Typ ICE startet um 14 Uhr am Frankfurter Hauptbahnhof. Die Entwicklung der Geschwindigkeit des ICE kann für $x \geq 0$ zunächst modellhaft durch die Funktion $v$ mit $v ( x )=\dfrac{250}{1+24 \cdot \mathrm e ^{-0,9 x }}-10$ beschrieben werden.
Dabei ist $x$ die seit 14:00 Uhr vergangene Zeit in Minuten und $v ( x )$ die Geschwindigkeit in Kilometer pro Stunde.

1.1

Zeige, dass der ICE mit einer Geschwindigkeit von $0 \,\text{km/h}$ startet und langfristig eine Reisegeschwindigkeit von $v_R=240 \,\text{km/h}$ erreicht.

(4 BE)

1.2

Berechne den Zeitpunkt $x$ , zu dem der ICE $90 \,\%$ der Geschwindigkeit $v_R$ erreicht.
Die Abbildung im Material 1 zeigt den Graphen von $v$ . Beschrifte die Koordinatenachsen mit der fehlenden Skalierung.

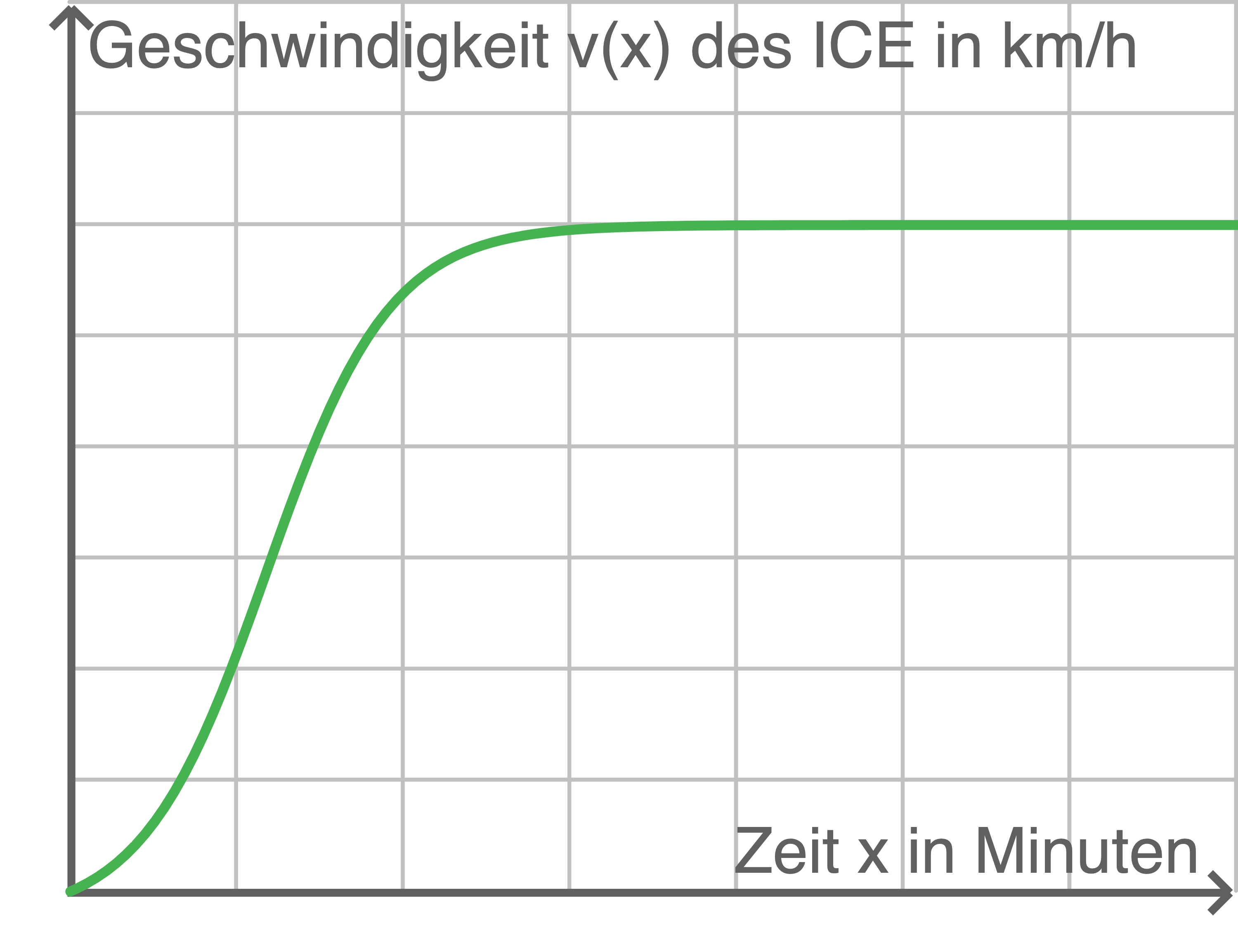
hessen mathe abi lk cas 2022 teil b1 abbildung 1

Material 1

(6 BE)

Der ICE fährt im weiteren Verlauf seiner Fahrt von 14:30 Uhr bis 15:00 Uhr mit konstanter Geschwindigkeit. Von 15:00 Uhr bis 15:02 Uhr nimmt seine Geschwindigkeit ab. Ab 15:02 Uhr fährt der ICE wieder mit konstanter Geschwindigkeit. Zur modellhaften Beschreibung der Entwicklung der Geschwindigkeit des ICE im Zeitraum von 15:00 Uhr bis 15:02 Uhr wird eine Schar ganzrationaler Funktionen betrachtet.

2.1

Die Geschwindigkeitsentwicklung von 15:00 Uhr bis 15:02 Uhr wird zunächst mithilfe der in $\mathbb{R}$ definierten Funktion $f$ der Schar mit $f(x)=30 x^{3}-90 x^{2}+240$ beschrieben. Dabei ist $x$ die seit 15:00 Uhr vergangene Zeit in Minuten und $f(x)$ die Geschwindigkeit in Kilometer pro Stunde.
Die Abbildung in Material 2 zeigt für $0 \leq x \leq 2$ den Graphen von $f$ ; außerdem stellt sie die Geschwindigkeiten des ICE kurz vor 15:00 Uhr und nach 15:02 Uhr dar.

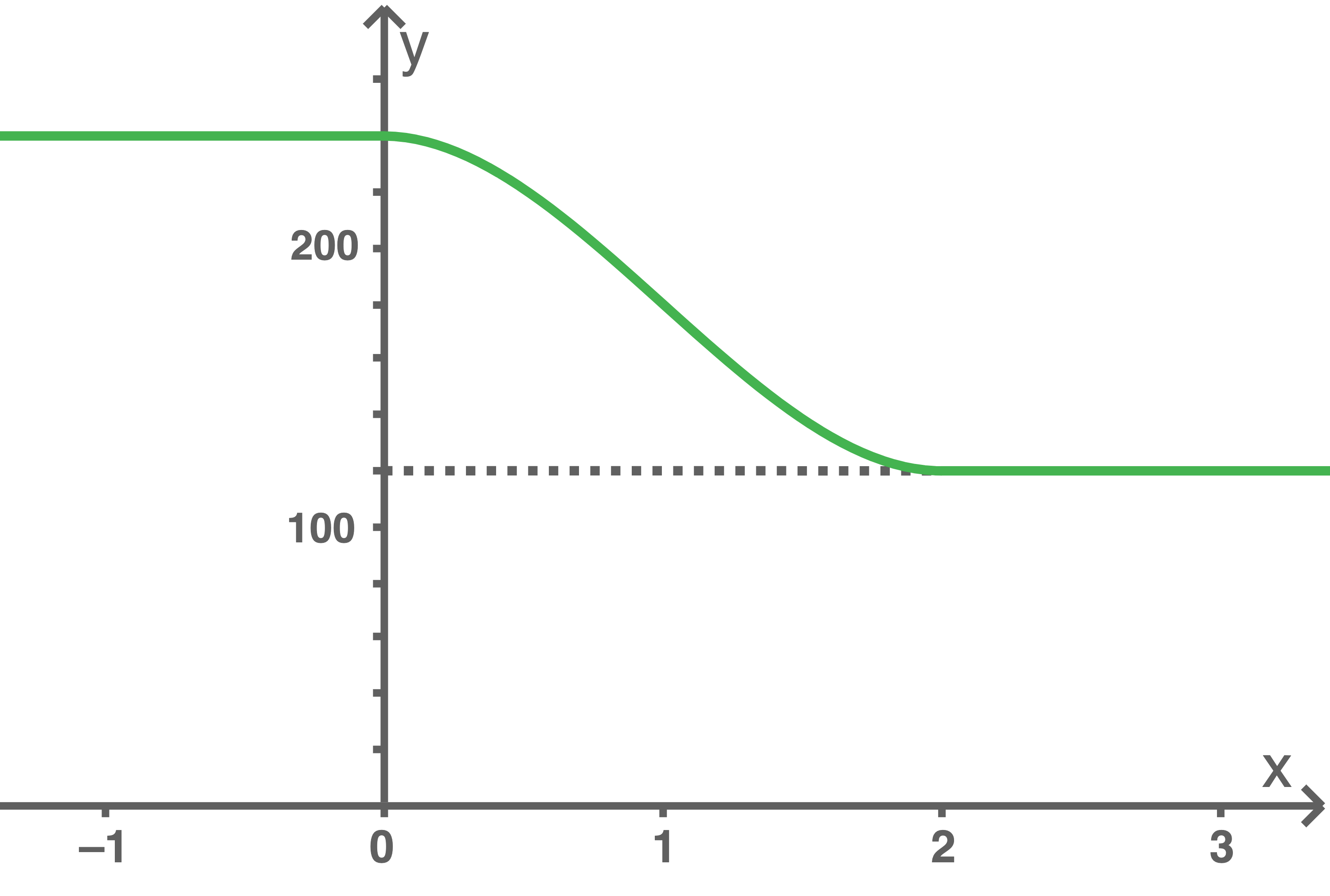
ni abi ea gtr 2022 teil 1 abbildung 1 zug ice

Material 2

2.1.1

Bestimme die Geschwindigkeit, die der ICE eine halbe Minute nach 15:00 Uhr hat.
Zeige, dass die Geschwindigkeit in der ersten halben Minute nach 15:00 Uhr um einen kleineren Betrag abnimmt als in der darauf folgenden halben Minute.

(4 BE)

2.1.2

Ermittle den Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt.

(2 BE)

2.1.3

Bestimme einen Zeitraum, der frühestens um 14:59 Uhr beginnt und spätestens um 15:03 Uhr endet, in dem der ICE eine Strecke mit einer Länge von genau $7 \,\text{km}$ zurücklegt.

(5 BE)

2.1.4

Untersuche, ob die folgende Aussage richtig ist:
„Wenn sich die Abnahme der Geschwindigkeit von 15:01 Uhr an nicht mehr verändern würde, dann käme der ICE von diesem Zeitpunkt an nach drei Kilometern zum Stehen.“

(4 BE)

2.2

Nun werden alle in $\mathbb{R}$ definierten Funktionen $f_p$ der Schar mit

Schar anzeigen

und $p \in \mathbb{R}$ daraufhin untersucht, ob sie für $0 \leq x \leq 2$ die Entwicklung der Geschwindigkeit des ICE von 15:00 Uhr bis 15:02 Uhr passend beschreiben könnten.

2.2.1

Der Übergang von der Fahrt mit konstanter Geschwindigkeit kurz vor 15:00 Uhr zur Fahrt nach 15:00 Uhr erfolgt sowohl hinsichtlich der Geschwindigkeit als auch hinsichtlich der momentanen Änderungsrate der Geschwindigkeit ohne Sprung. Die Funktionen $f_p$ werden diesen beiden Anforderungen gerecht.
Gib die zugehörigen Bedingungen an, die die Funktionen $f_{p}$ erfüllen.

(2 BE)

2.2.2

Gib denjenigen Wert von $p$ an, für den $f_p(x)$ mit dem Term der Funktion $f$ übereinstimmt.
Beurteile für jede der Funktionen $f _{-80}$ und $f_{250}$ mithilfe des zugehörigen Graphen, ob die Funktion die Geschwindigkeitsentwicklung innerhalb des Zeitraums von 15:00 Uhr bis 15:02 Uhr passend beschreiben könnte.
Hinweis: Eine Skizze der Graphen ist nicht erforderlich.

(4 BE)

2.2.3

Gegeben sind die folgenden Informationen:
Für $p \neq 0$ liefert $f _{ p }^{\prime}( x )=0$ neben $x_1=0$ und $x _2=2$ die Lösung $x_3=1-\dfrac{90}{p}$ .
Es gilt $x _{3} \leq 0 \Leftrightarrow 0\lt p \leq 90$ und $x _{3} \geq 2 \Leftrightarrow-90 \leq p \lt0$ .
Beurteile auch unter Verwendung dieser Informationen die Funktionen $f_{p}$ mit $p \neq 0$ im Hinblick auf ihre Eignung zur Beschreibung der angenommenen Geschwindigkeitsentwicklung innerhalb des Zeitraums von 15:00 Uhr bis 15:02 Uhr.

(4 BE)

Betrachtet wird die in $\mathbb{R}$ definierte Funktion $s$ mit $s(x)= a \cdot \sin ( b \cdot x )+ c$ . Die Punkte $E_{1}(-2 \mid-1)$ und $E_{2}(2 \mid 3)$ sind direkt aufeinanderfolgende Extrempunkte des Graphen von $s.$

3.1

Bestimme die passenden Werte von $a$ , $b$ und $c$ .
[ Zur Kontrolle: $a =2, b =\frac{\pi}{4}, c =1$ ]

(4 BE)

3.2

Gib den Wert des Terms $\displaystyle\int_{-2}^{2}s(x)\;\mathrm dx$ an.

Beschreibe mithilfe der Abbildung in Material 3, wie man zu diesem Wert mit geometrischen Überlegungen gelangen kann.
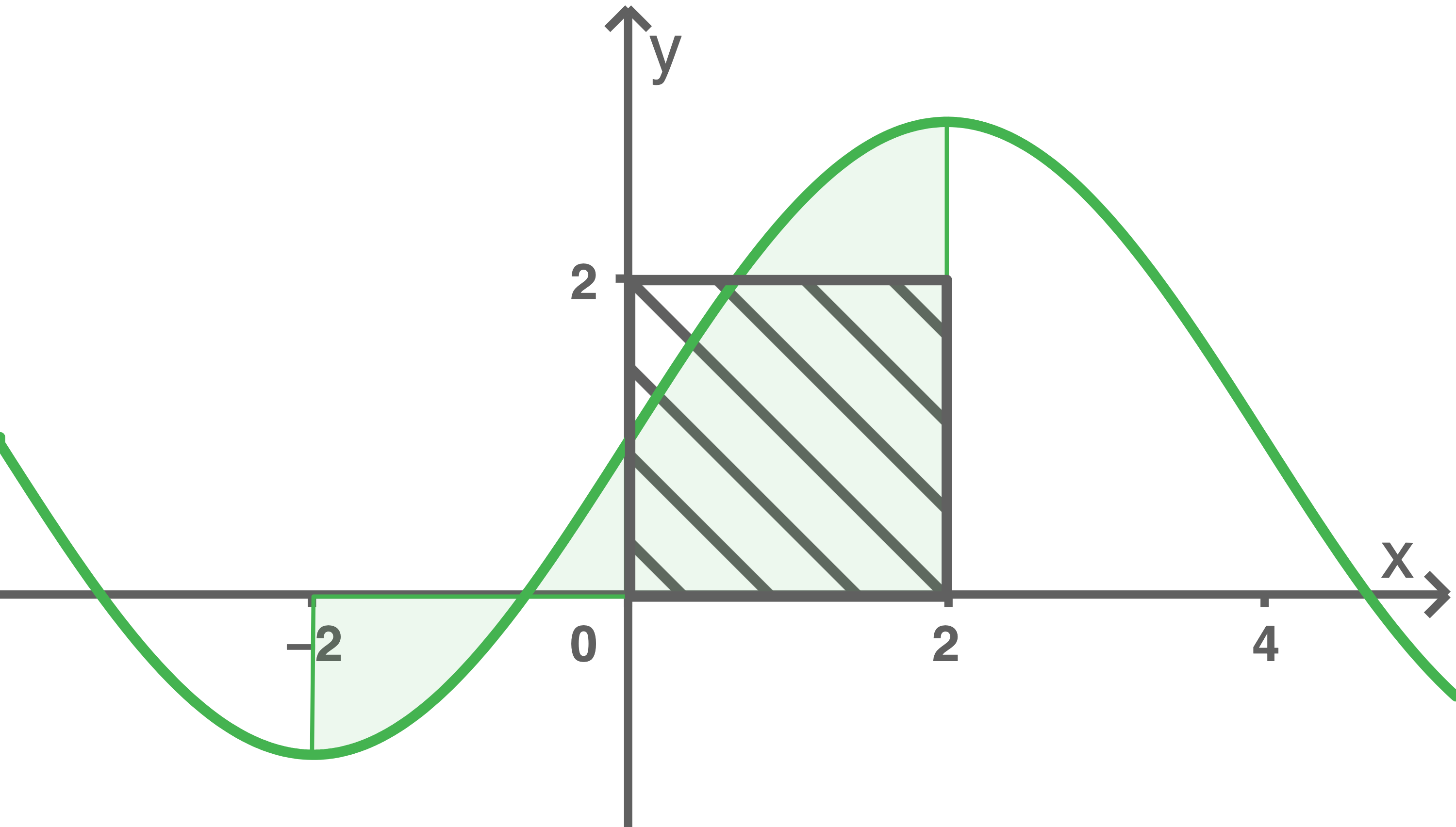
Hinweis: Zur Erleichterung der Beschreibung kann die Abbildung in Material 3 geeignet beschriftet werden.

Material 3

(6 BE)

Die Punkte des Graphen von $s$ mit der $y$ -Koordinate $1$ sind die Wendepunkte des Graphen.

3.3

Zeige, dass jeder Wendepunkt des Graphen von $s$ eine ganzzahlige $x$ -Koordinate hat und dass der Graph von $s$ in jedem seiner Wendepunkte entweder die Steigung $-\dfrac{\pi}{2}$ oder die Steigung $+\dfrac{\pi}{2}$ hat.

(2 BE)

3.4

Für jeden Wendepunkt des Graphen von $s$ wird die Gerade betrachtet, die durch diesen Wendepunkt und den Punkt $P(2022 \mid 2022)$ verläuft. Untersuche, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den Graphen von $s$ ist.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Startgeschwindigkeit berechnen

$\begin{array}[t]{rll} v(0)&=&\dfrac{250}{1+24 \cdot \mathrm{e}^{-0,9 \cdot 0}}-10 & \\[5pt] &=&\dfrac{250}{25}-10 & \\[5pt] &=& 0 \end{array}$

Der ICE startet folglich mit einer Geschwindigkeit von $0 \frac{\,\text{km}}{\,\text{h}}.$

Langfristige Reisegeschwindigkeit bestimmen

$\begin{array}[t]{rll} v_r&=& \lim\limits_{x\to\infty}\dfrac{250}{1+24 \cdot \mathrm{e}^{-0,9 \cdot x}}-10& \\[5pt] &=& \dfrac{250}{1+24 \cdot 0}-10& \\[5pt] &=&240 \; [\frac{\,\text{km}}{\,\text{h}}] \end{array}$

Somit erreicht der ICE eine langfristige Geschwindigkeit von $v_r=240 \; \frac{\,\text{km}}{\,\text{h}} .$

1.2

Es gilt:

$0,9\cdot 240 \frac{\,\text{km}}{\,\text{h}}=216 \frac{\,\text{km}}{\,\text{h}}$

Der Zeitpunkt $x$ lässt sich nun durch Lösen folgender Gleichung berechnen:

$\begin{array}[t]{rll} v(x)&=& 216 & \\[5pt] \dfrac{250}{1+24 \cdot \mathrm{e}^{-0,9 \cdot x}}-10 &=& 216 \\[5pt] \end{array}$

Mit dem solve-Befehl des CAS ergibt sich der Zeitpunkt $x\approx 6.$

Der ICE erreicht $90\,\%%$ der Geschwindigkeit $v_R$ nach 6 Minuten.

Skalierung der Koordinatenachsen:

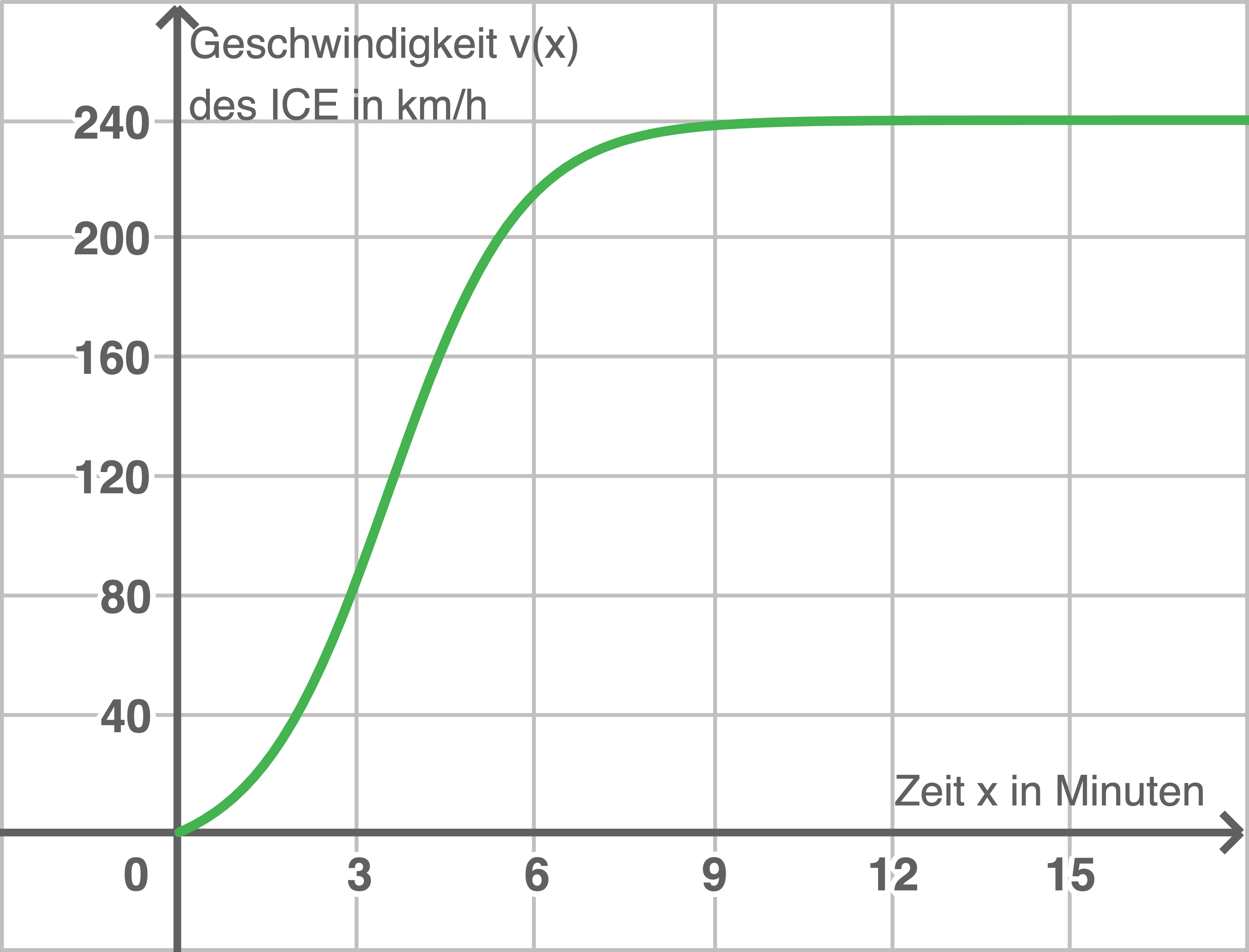
2.1.1

Bestimmung der Geschwindigkeit

$f(0,5) = 30 \cdot 0,5^3 - 90 \cdot 0,5^2 + 240$
$f(0,5) = 221,25$

Die Geschwindigkeit des ICE beträgt eine halbe Minute nach 15:00 ca. $221 \; \frac{\text{km}}{\text{h}}.$

Bestimmung der Geschwindigkeitsabnahme im ersten Intervall

$f(0)-f(0,5)= 30 \cdot 0^3 - 90 \cdot 0^2 + 240 - 221,25$
$f(0)-f(0,5)= 18,75$

Bestimmung der Geschwindigkeitsabnahme im zweiten Intervall

$f(0,5)-f(1)= 30 \cdot 0,5^3 - 90 \cdot 0,5^2 + 240 - (30\cdot 1^3-90\cdot 1^2+240)$
$f(0,5)-f(1)= 41,25$

Folglich nimmt die Geschwindigkeit in der ersten halben Minute um einen kleineren Betrag ab als in der darauf folgenden halben Minute.

2.1.2

Die stärkste Geschwindigkeitsabnahme entspricht dem Wendepunkt von $f.$

Die gesuchte Wendestelle von $f$ entspricht dem Minimum von $\(f$

$\blacktriangleright$ TI nspire CAS

menu $\to$ 6: Graph analysieren $\to$ 3: Minimum

$\blacktriangleright$ Casio Classpad II

Analyse $\to$ Grafische Lösung $\to$ Minimum

Mit dem CAS folgt hierfür: $t=1$

Nun ist noch die hinreichende Bedingung zu prüfen. Hierfür muss die dritte Ableitung gebildet werden.

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

Durch Einsetzen von $t=1$ in die dritte Ableitung folgt:

$\(f$

2.1.3

Die zurückgelegte Strecke $s$ entspricht dem Flächeninhalt der Fläche, die der Graph mit der $x$ -Achse einschließt. Bei der Strecke muss beachtet werden, dass die $x$ -Achse in $\text{min}$ angegeben ist und die $y$ -Achse in $\frac{\text{km}}{\text{h}}$ angegeben ist.

Bei Beginn eines solchen Zeitraums beispielsweise um 15:00 Uhr ergibt sich:

$\begin{array}[t]{rll} s&=& \dfrac{1}{60} \cdot \displaystyle\int_{0}^{2}f(x)\;\mathrm dx \\[5pt] &=& \dfrac{1}{60} \cdot \left[7,5x^4 - 30x^3+240 \right]_0^2 \\[5pt] &=& 6 \; [\text{km}] \end{array}$

Der Zug hat bis 15:02 Uhr $6 \text{ km}$ zurückgelegt. Folglich muss noch der Zeitpunkt bestimmt werden, an dem der Zug einen weiteren Kilometer zurückgelegt hat.

$\begin{array}[t]{rll} \dfrac{1}{60} \cdot f(2) \cdot t&=& 1 \\[5pt] \dfrac{1}{60} \cdot 120 \cdot t&=& 1 \\[5pt] 2 \cdot t&=& 1 &\quad \scriptsize \mid\; :2 \\[5pt] t&=& 0,5 \end{array}$

Somit endet der Zeitraum, der um 15:00 Uhr beginnt nach $2+0,5=2,5$ Minuten.

In diesem Zeitraum wurden $7 \,\text{km}$ zurückgelegt.

2.1.4

Die Tangente des Graphen von $f$ an der Stelle $x_0=1$ wird auf Nullstellen untersucht.

Aufstellen der Tangentengleichung

$\(\begin{array}[t]{rll} y&=& f$

Nullstelle der Tangente

$\begin{array}[t]{rll} -90 \cdot x+ 270 &=& 0 &\quad \scriptsize \mid\; -270 \\[5pt] -90 \cdot x &=& -270 &\quad \scriptsize \mid\; :90 \\[5pt] x &=& 3 \end{array}$

Zurückgelegte Strecke

Die zurückgelegte Strecke $s$ entspricht dem Flächeninhalt der Fläche, die der Graph von $y$ mit der $x$ -Achse im Intervall $[1;3]$ einschließt. Bei der Strecke muss beachtet werden, dass die $x$ -Achse in $\text{min}$ angegeben ist und die $y$ -Achse in $\frac{\text{km}}{\text{h}}$ angegeben ist.

$\begin{array}[t]{rll} s&=& \dfrac{1}{60} \cdot \dfrac{1}{2} \cdot 2 \cdot f(1)\\[5pt] s&=& \dfrac{1}{60} \cdot 180 \\[5pt] s&=& 3 \; [\text{km}] \end{array}$

Die Aussage ist richtig.

2.2.1

Die Funktion $f_p$ muss folgende Bedingungen erfüllen:

$f_p(0)=v(0)=240$ und $\(f_p$

2.2.2

Wert von $p$ bestimmen

Es muss gelten:

Rechenweg anzeigen

$f(x)= f_p(x)$

Da in die Funktion $f$ nur den Grad $3$ besitzt und die Funktion $f_p$ den Grad 4, folgt:

$\frac{p}{4} \cdot x^4=0$ und somit $p=0$

Überprüfen durch Einsetzen von $p=0$ in $f_p:$

Rechenweg anzeigen

$f_0(x)=f(x)$

Für den Wert $p=0$ stimmt folglich $f_p(x)$ mit dem Term von $f$ überein.

Beurteilung der Graphen

Graph von $f_{-80}:$

Die Funktion $f_{-80}$ könnte die Geschwindigkeitsentwicklung im Zeitraum von 15:00 bis 15:02 passend beschreiben: Der Graph ist in diesem Intervall monoton fallend, somit nimmt die Geschwindigkeit des ICEs wie in der Voraussetzung ab.

Graph von $f_{250}:$

Die Funktion $f_{250}$ beschreibt die Geschwindigkeitsentwicklung im Zeitraum von 15:00 bis 15:02 nicht passend: Die Geschwindigkeit würde zuerst ansteigen und dann wieder abfallen, was der Aussage widerspricht, dass der ICE in diesem Zeitabschnitt mit abnehmender Geschwindigkeit fährt.

2.2.3

Für $0 \lt p \leq 90$ befindet sich eine weitere Extremstelle von $f_p$ bei $x_3 \leq 0,$ für $-90\leq p \lt 0$ ist diese $x_3 \geq 2$ und somit in beiden Fällen nicht im Zeitraum von 15:00 bis 15:02.

Eine Extremstelle bedeutet, dass ein Vorzeichenwechsel stattfindet und der Graph folglich zeitweise ansteigen würde.

Für $p\lt -90$ und $p\gt 90$ würde die Extremstelle $x_3$ somit im Zeitraum von 15:00 bis 15:02 den Graphen so verändern, dass dieser ansteigt und die Geschwindigkeit zunimmt. Folglich sind diese Werte von $p$ ungeeignet für die Beschreibung der angenommenen Geschwindigkeitsentwicklung.

3.1

Berechung von a

Der Parameter $a$ gibt die Streckung entlang der $y$ -Achse an. Dieser ergibt sich aus der halbierten Differenz der $y$ -Werte der beiden aufeinanderfolgenden Extrempunkte.

$\begin{array}[t]{rll} a &=& \dfrac{1}{2} \cdot (3 - (-1)) \\[5pt] a &=& 2 \end{array}$

Berechung von b

Der Parameter $b$ gibt die Streckung entlang der $x$ -Achse an.

$\begin{array}[t]{rll} b &=& \dfrac{\pi}{2-(-2)} \\[5pt] b &=& \dfrac{\pi}{4} \\[5pt] \end{array}$

Berechung von c

Der Parameter $c$ gibt die Verschiebung entlang der $y$ -Achse an. Dieser ergibt sich aus dem Mittelwert der $y$ -Werte der beiden aufeinanderfolgenden Extrempunkte.

$\begin{array}[t]{rll} c &=& \dfrac{1}{2} \cdot (3 + (-1)) \\[5pt] c &=& 1 \end{array}$

3.2

Wert des Terms berechnen

Geometrische Überlegungen beschreiben

Der Graph von $s$ ist symmetrisch bezüglich des Punktes $(0\mid 1).$ Damit haben die Flächenstücke $A_{1}$ und $A_{4}$ ebenso den gleichen Inhalt wie die Flächenstücke $A_{2}$ und $A_{3}.$

Aufgrund der Lage dieser Flächenstücke bezüglich der $x$ -Achse und bezüglich des abgebildeten Quadrats, stimmt der Wert des Terms mit dem Flächeninhalt des Quadrats überein, ist also $2^{2}=4$ .

Also gilt:

$\displaystyle\int_{-2}^{2}s(x)\;\mathrm dx = 4$

3.3

1. Schritt: $x$ -Koordinate der Wendepunkte bestimmen

$\begin{array}[t]{rll} 1&=&2\cdot \sin\left(\dfrac{\pi}{4}\cdot x\right)+1 &\quad \scriptsize \mid\; -1 \quad \scriptsize \mid\;:2\\[5pt] 0&=&\sin\left(\dfrac{\pi}{4}\cdot x\right)&\quad \scriptsize \mid\;\arcsin \\[5pt] 0&=&\dfrac{\pi}{4}\cdot x \quad \scriptsize \mid\;:\left(\dfrac{\pi}{4}\right)\\[5pt] 0&=& x \end{array}$

Mit der Periode $p=\dfrac{2\pi}{\dfrac{\pi}{4}}=8$ folgen die Koordinaten der Wendepunkte mit $W(4k\mid 1)$ mit $k \in \mathbb{Z}$ .

2. Schritt: Steigung an den Wendepunkten berechnen

Steigung am Punkt $W(0\mid 1):$

$\(\begin{array}[t]{rll} s$

Aufgrund des Verlaufes der Sinusfunktion folgt, dass ebenso alle weiteren Wendepunkte im Wechsel eine Steigung von $\dfrac{\pi}{2}$ oder $-\dfrac{\pi}{2}$ haben.

3.4

Koordinaten der Wendepunkte

Der Aufgabenstellung kann entnommen werden, dass die Wendepunkte die Koordinaten $(4k \mid 1)$ mit $k \in \mathbb{Z}$ besitzen.

Steigung der Geraden

Die betrachteten Geraden haben folgende Steigung:

$\begin{array}[t]{rll} m &=& \dfrac{\Delta y}{\Delta x}\\[5pt] m &=& \dfrac{2022 - 1}{2022-4k} \\[5pt] m &=& \dfrac{2021}{2022-4k} \\[5pt] \end{array}$

Folglich ist die Steigung für jedes $k \in \mathbb{Z}$ rational. Die Steigung in den Wendestellen ist nach Aufgabenstellung $\pm \frac{\pi}{2}$ und somit irrational. Folglich ist keine der Geraden eine Tangente einer Wendestelle.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?