A – Wahlaufgaben
Analysis (Niveau 2)
5
Gegeben ist für jede positive reelle Zahl  die in
die in  definierte Funktion
definierte Funktion  mit
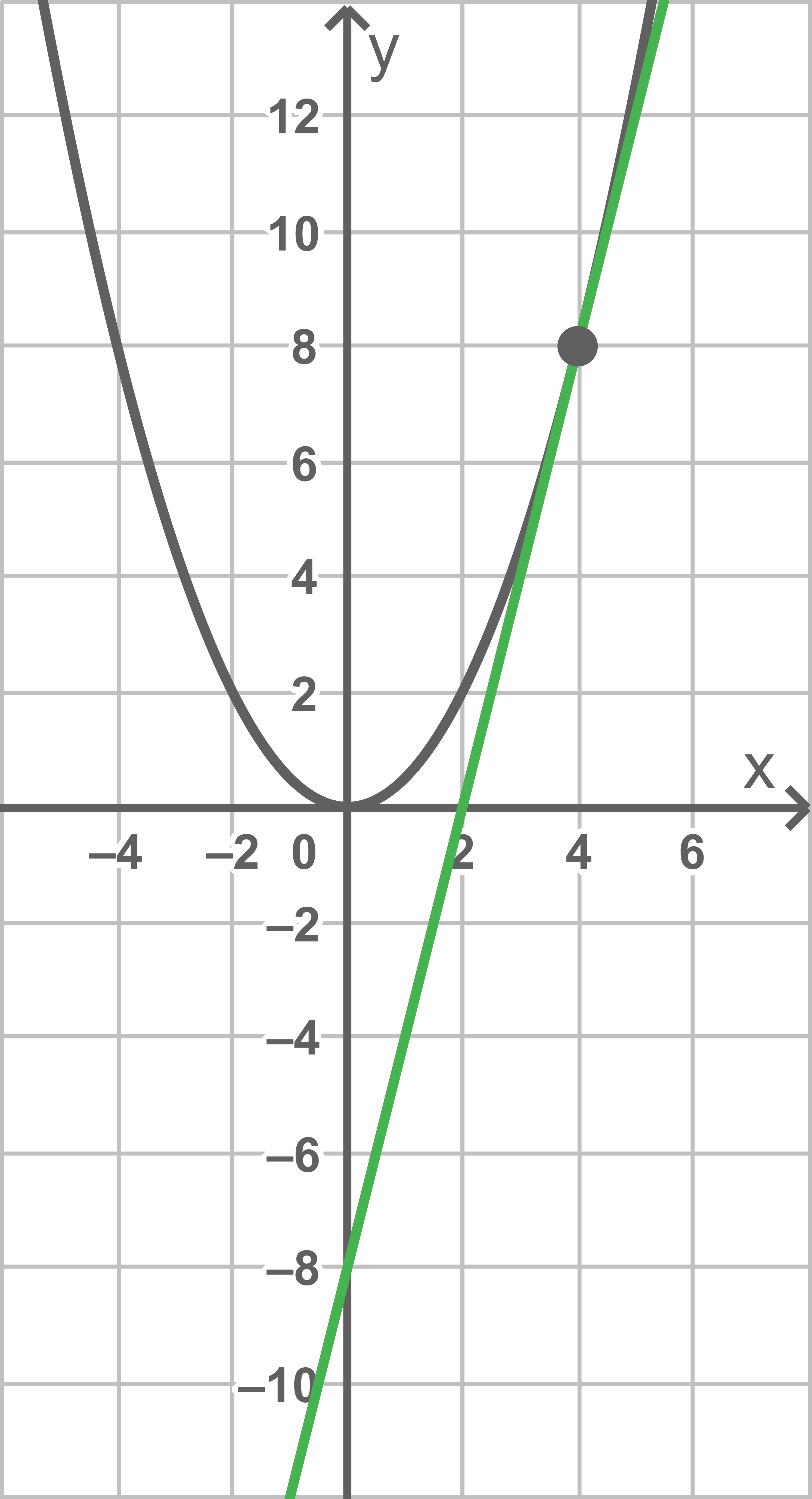
mit  Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von  sowie die Tangente
sowie die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt 

5.1
Gib anhand der Abbildung eine Gleichung der Tangente  an.
an.
(1 BE)
5.2
Weise nach, dass für jeden Wert  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse im Punkt
-Achse im Punkt  schneidet.
schneidet.
(4 BE)
Analysis (Niveau 2)
6
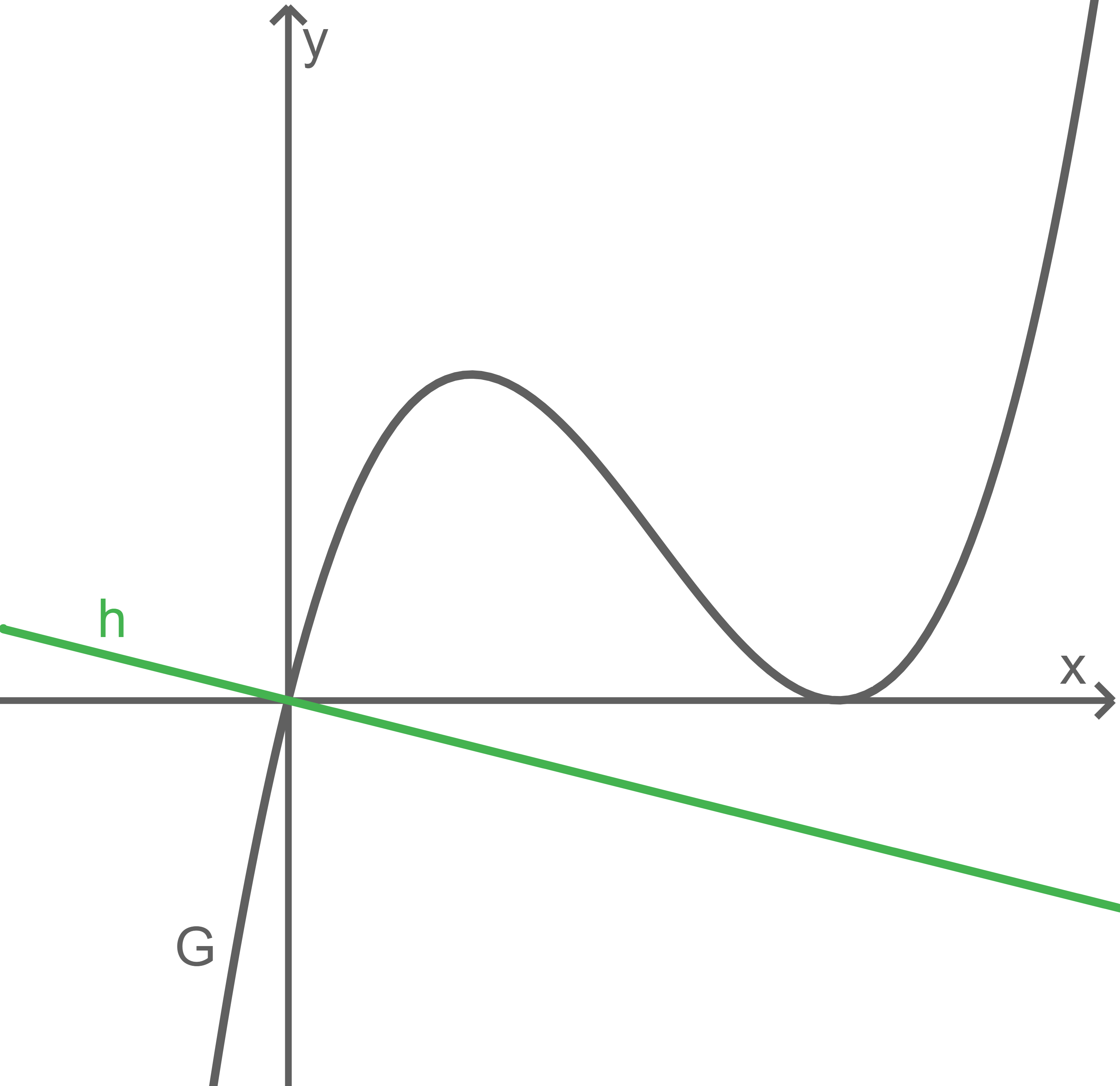
Für eine Zahl  zeigt die Abbildung den Graphen
zeigt die Abbildung den Graphen  der in
der in  definierten Funktion
definierten Funktion  mit
mit  sowie die Gerade
sowie die Gerade 
 und
und  schneiden sich im Koordinatenursprung und
schneiden sich im Koordinatenursprung und  verläuft senkrecht zur Tangente an
verläuft senkrecht zur Tangente an  im Koordinatenursprung. Zudem berühren sich
im Koordinatenursprung. Zudem berühren sich  und die
und die  -Achse im Punkt
-Achse im Punkt  Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
- Die beiden gemeinsamen Punkte von
und der
-Achse sind zwei benachbarte Eckpunkte des Rechtecks.
- Eine Diagonale liegt auf der Gerade
(5 BE)
Lineare Algebra / Analytische Geometrie (Niveau 2)
7
Die Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung).
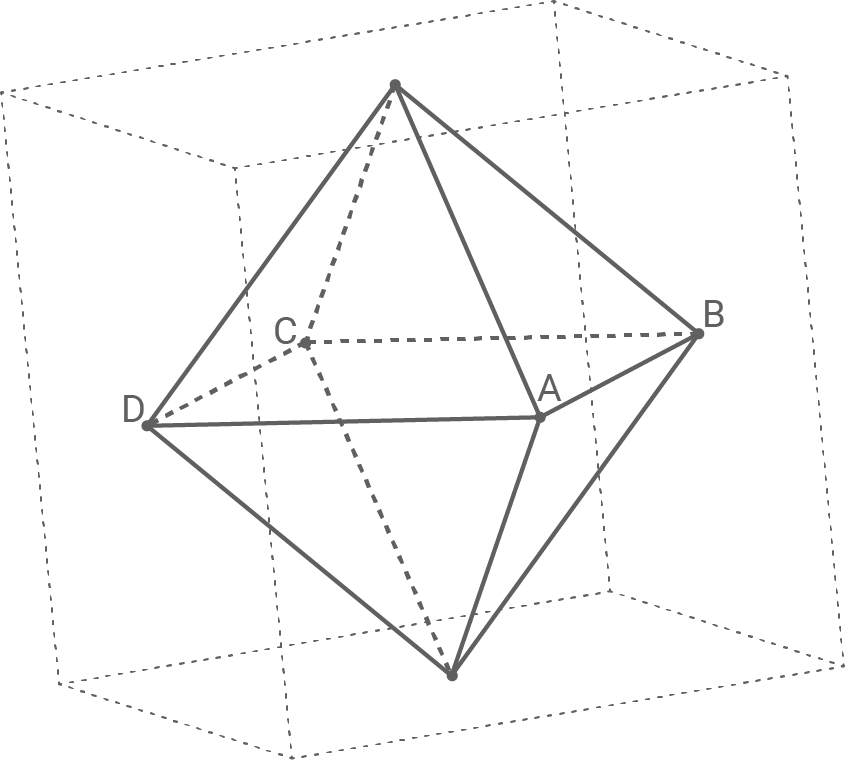 Die Eckpunkte
Die Eckpunkte 

 und
und  des Oktaeders liegen in der Ebene
des Oktaeders liegen in der Ebene  mit der Gleichung
mit der Gleichung 

7.1
Weise nach, dass die Kantenlänge des Würfels 12 beträgt.
(2 BE)
7.2
Bestimme die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in  liegen.
liegen.
(3 BE)
Lineare Algebra / Analytische Geometrie (Niveau 2)
8
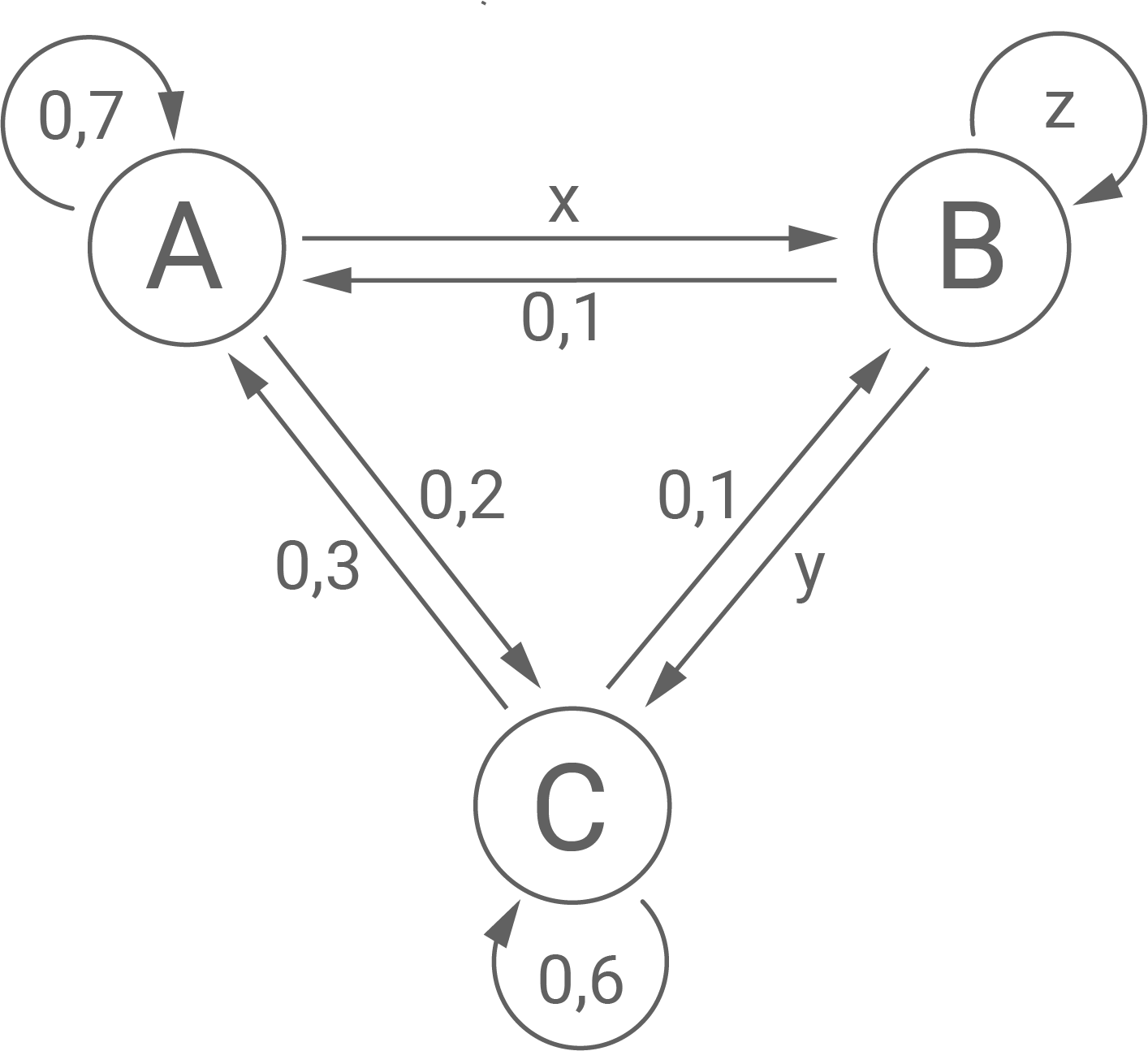
Das abgebildete Übergangsdiagramm zeigt die in einer Untersuchung ermittelten Kundenströme zwischen drei Supermarktketten von einem Monat zum nächsten.
Zu Beginn der Untersuchung hatte die Supermarktkette A  Kunden, B hatte
Kunden, B hatte  Kunden und C hatte
Kunden und C hatte  Kunden.
Einen Monat nach Beginn der Untersuchung hatte die Supermarktkette A
Kunden.
Einen Monat nach Beginn der Untersuchung hatte die Supermarktkette A  Kunden, B hatte
Kunden, B hatte  Kunden und C hatte
Kunden und C hatte  Kunden.
Kunden.
8.1
Im Modell wird die Verteilung der Kunden auf die drei Supermarktketten durch Vektoren der Form  dargestellt, wobei
dargestellt, wobei  jeweils die Anzahl der Kunden der Supermarktketten A, B und C bezeichnen.
Die Entwicklung der Kundenverteilung von einem Monat zum nächsten kann mit Hilfe einer geeigneten Übergangsmatrix
jeweils die Anzahl der Kunden der Supermarktketten A, B und C bezeichnen.
Die Entwicklung der Kundenverteilung von einem Monat zum nächsten kann mit Hilfe einer geeigneten Übergangsmatrix  durch die Gleichung
durch die Gleichung  beschrieben werden.
Berechne die resultierenden Werte für
beschrieben werden.
Berechne die resultierenden Werte für  und
und  (Abbildung) und gib die vollständige Übergangsmatrix
(Abbildung) und gib die vollständige Übergangsmatrix  an.
an.
(3 BE)
8.2
Für die Matrix  gilt
gilt  Erläutere, was dies im Sachzusammenhang für die langfristige Entwicklung der Kundenverteilung bedeutet.
Erläutere, was dies im Sachzusammenhang für die langfristige Entwicklung der Kundenverteilung bedeutet.
(2 BE)
Stochastik (Niveau 2)
9
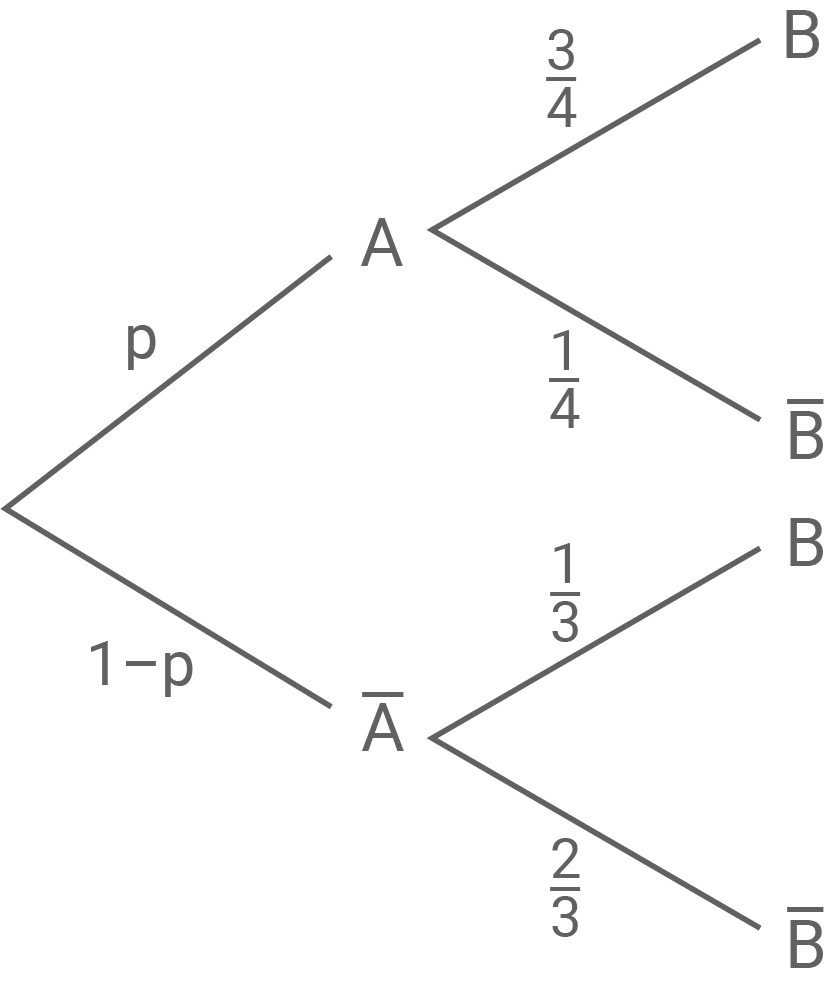
Das abgebildete Baumdiagramm stellt ein zweistufiges Zufallsexperiment mit den Ereignissen A und B sowie den zugehörigen Gegenereignissen dar.
Es gilt  Berechne die Wahrscheinlichkeit
Berechne die Wahrscheinlichkeit  und gib eine zu diesem Zufallsexperiment zugehörige Vierfeldertafel an.
und gib eine zu diesem Zufallsexperiment zugehörige Vierfeldertafel an.
 zur Kontrolle:
zur Kontrolle: ![\(p=0,4 \big]\)](https://mathjax.schullv.de/74e27c9c715be44e9111b2da397d3edfc6bd748924768cbf81dc0e91b07ebdc2?color=5a5a5a)
(5 BE)
Stochastik (Niveau 2)
10
Die sechs Seiten eines verfälschten Würfels sind mit den Zahlen  beschriftet.
Der Würfel ist so gefertigt, dass bei einmaligem Werfen die Wahrscheinlichkeit für das Erzielen der Zahl
beschriftet.
Der Würfel ist so gefertigt, dass bei einmaligem Werfen die Wahrscheinlichkeit für das Erzielen der Zahl  jeweils doppelt so groß ist wie die Wahrscheinlichkeit für das Erzielen der Zahl
jeweils doppelt so groß ist wie die Wahrscheinlichkeit für das Erzielen der Zahl 
 Der Würfel wird 6300-mal geworfen.
Leite den Erwartungswert der Summe der erzielten Zahlen rechnerisch her.
Der Würfel wird 6300-mal geworfen.
Leite den Erwartungswert der Summe der erzielten Zahlen rechnerisch her.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Analysis (Niveau 2)
5.1
Aus der Abbildung kann die Steigung  sowie der
sowie der  -Achsenabschnitt der Tangente bei
-Achsenabschnitt der Tangente bei  abgelesen werden.
Eine Gleichung der Tangente ist somit
abgelesen werden.
Eine Gleichung der Tangente ist somit 
5.2
Analysis (Niveau 2)
6
Rechteck skizzieren
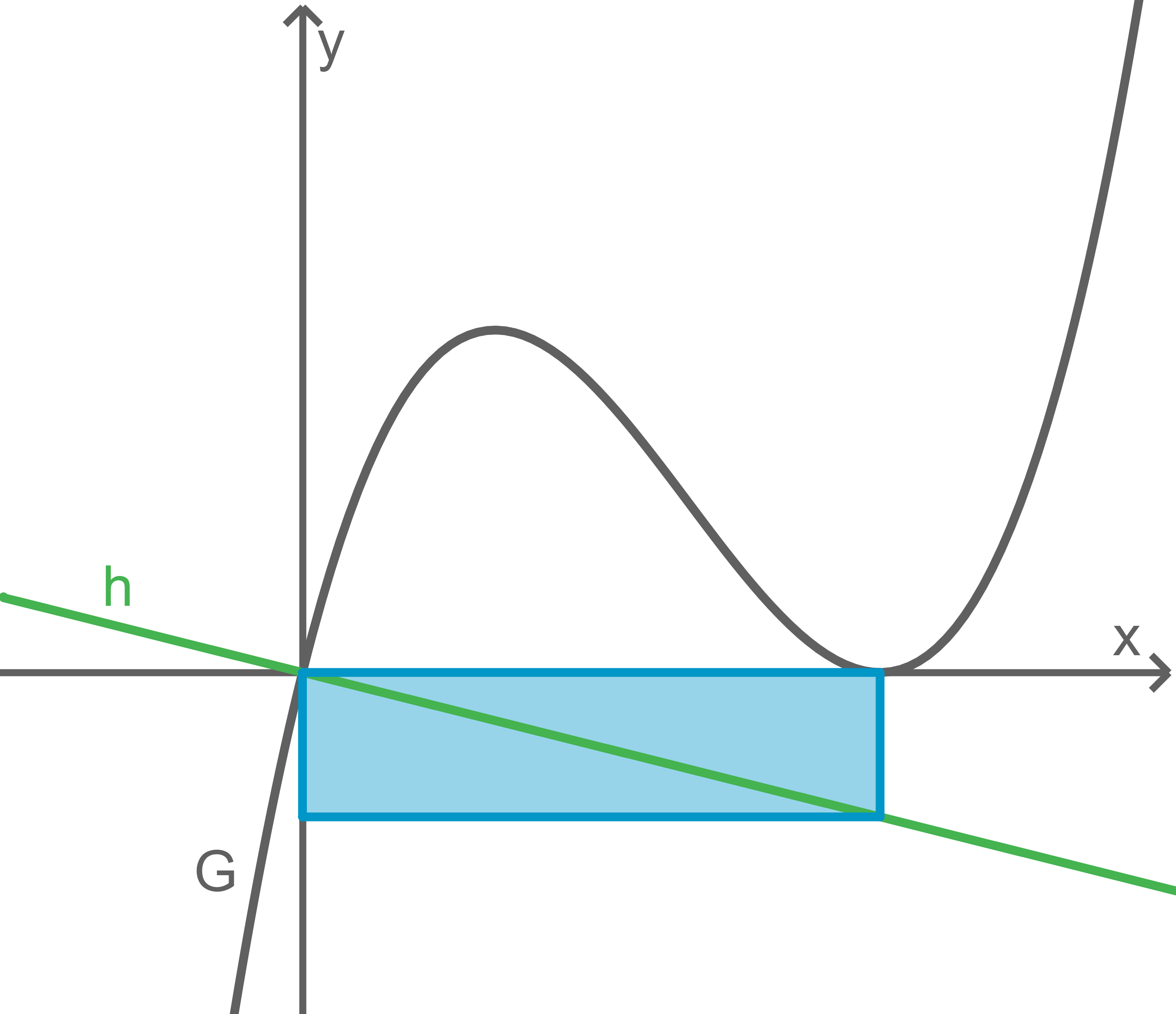 Unabhängigkeit des Flächeninhalts zeigen
Die Länge der Seite des Rechtecks, die auf der
Unabhängigkeit des Flächeninhalts zeigen
Die Länge der Seite des Rechtecks, die auf der  -Achse verläuft, ergibt sich durch die Differenz der
-Achse verläuft, ergibt sich durch die Differenz der  -Werte der beiden Punkte, in denen
-Werte der beiden Punkte, in denen  die
die  -Achse berührt, als
-Achse berührt, als  Für die Ableitung der Funktion
Für die Ableitung der Funktion  gilt:
gilt:
 Da
Da  senkrecht zur Tangente an
senkrecht zur Tangente an  im Koordinatenursprung verläuft, ergibt sich mit Hilfe von
im Koordinatenursprung verläuft, ergibt sich mit Hilfe von  die Steigung von
die Steigung von  als
als  Somit folgt
Somit folgt  Für die Länge der kürzeren Rechteckseite folgt damit:
Für die Länge der kürzeren Rechteckseite folgt damit:
 Damit folgt für den Flächeninhalt
Damit folgt für den Flächeninhalt  des Rechtecks
des Rechtecks  womit dieser unabhängig von
womit dieser unabhängig von  ist.
ist.

Lineare Algebra / Analytische Geometrie (Niveau 2)
7.1
7.2
Die beiden Eckpunkte, die nicht in  liegen, sind die obere bzw. untere Spitze des Oktaeders und stehen senkrecht über bzw. unter dem Mittelpunkt
liegen, sind die obere bzw. untere Spitze des Oktaeders und stehen senkrecht über bzw. unter dem Mittelpunkt  der Fläche
der Fläche  Der Ortsvektor des Mittelpunkts
Der Ortsvektor des Mittelpunkts  der Strecke
der Strecke  ergibt sich zu:
ergibt sich zu:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt]
&=&\pmatrix{1\\2\\1}+\dfrac{1}{2}\cdot\pmatrix{-4\\-8\\8} \\[5pt]
&=&\pmatrix{-1\\-2\\5}
\end{array}\)](https://mathjax.schullv.de/f13901135af0ed1192f659481eb360c4523f0a812f6d7c78db8b4d46d714bd89?color=5a5a5a) Aus der Ebenengleichung von
Aus der Ebenengleichung von  lässt sich zudem der folgende Normalenvektor ablesen:
lässt sich zudem der folgende Normalenvektor ablesen:
 Für die Länge des Normalenvektors gilt
Für die Länge des Normalenvektors gilt  Da die Kantenlänge des Würfels
Da die Kantenlänge des Würfels  beträgt, ist der Abstand der Eckpunkte des Oktaeders zu
beträgt, ist der Abstand der Eckpunkte des Oktaeders zu  durch
durch  gegeben. Ein möglicher Ortsvektor der oberen bzw. unteren Spitze ergibt sich somit zu:
gegeben. Ein möglicher Ortsvektor der oberen bzw. unteren Spitze ergibt sich somit zu:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=& \overrightarrow{OM}\pm 2\cdot\overrightarrow{n}\\[5pt]
&=&\pmatrix{-1\\-2\\5} \pm 2\cdot\pmatrix{2\\1\\2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/731ffea99cbb555079f97d710cd84b4c52eb675862362377e962b20ba092327f?color=5a5a5a) Mögliche Koordinaten für einen der beiden gesuchten Punkte sind somit gegeben durch
Mögliche Koordinaten für einen der beiden gesuchten Punkte sind somit gegeben durch  bzw.
bzw. 
Lineare Algebra / Analytische Geometrie (Niveau 2)
8.1
Zu Beginn der Untersuchung gilt 
 und
und  Einen Monat nach Untersuchungsbeginn gilt
Einen Monat nach Untersuchungsbeginn gilt 
 und
und  Dem Übergangsdiagramm kann die folgende Übergangsmatrix
Dem Übergangsdiagramm kann die folgende Übergangsmatrix  entnommen werden:
entnommen werden:
 Da die Summe der Kundenströme für jede Supermarktkette und somit die Summe der Einträge jeder Spalte der Matrix 1 ergeben muss, folgt aus der ersten Spalte direkt:
Da die Summe der Kundenströme für jede Supermarktkette und somit die Summe der Einträge jeder Spalte der Matrix 1 ergeben muss, folgt aus der ersten Spalte direkt:
![\(\begin{array}[t]{rll}
0,7+x+0,2&=& 1 &\quad \scriptsize \mid\; -0,9\\[5pt]
x&=& 0,1
\end{array}\)](https://mathjax.schullv.de/199f2e1e68057369b91616dc489d765f4f0fd1dc5332d3d05d67f77fae479fd3?color=5a5a5a) Für
Für  gilt weiterhin:
Aus der zweiten Zeile folgt:
Aus der dritten Zeile ergibt sich zudem:
Mit den Werten
gilt weiterhin:
Aus der zweiten Zeile folgt:
Aus der dritten Zeile ergibt sich zudem:
Mit den Werten 
 und
und  ist die vollständige Übergangsmatrix
ist die vollständige Übergangsmatrix  somit gegeben durch:
somit gegeben durch:

8.2
Die Matrix  nähert sich einer konstanten Verteilung an, die darauf hinweist, dass die Kundenverteilung in der langfristigen Entwicklung stabil bleibt.
Alle Supermärkte werden langfristig also etwa den gleichen Anteil an Kunden halten.
nähert sich einer konstanten Verteilung an, die darauf hinweist, dass die Kundenverteilung in der langfristigen Entwicklung stabil bleibt.
Alle Supermärkte werden langfristig also etwa den gleichen Anteil an Kunden halten.
Stochastik (Niveau 2)
9
Wahrscheinlichkeit berechnen
Es gilt:
![\(\begin{array}[t]{rll}
P(B)&=& 0,5 & \\[5pt]
P(A \cap B) + P(\overline{A}\cap B)&=& 0,5 & \\[5pt]
p\cdot \dfrac{3}{4}+(1-p)\cdot \dfrac{1}{3} &=& 0,5 & \\[5pt]
p\cdot \dfrac{3}{4}+1\cdot \dfrac{1}{3}-p\cdot \dfrac{1}{3} &=& 0,5 & \\[5pt]
p\cdot \dfrac{9}{12}+ \dfrac{4}{12}-p\cdot \dfrac{4}{12} &=& \dfrac{6}{12} &\quad \scriptsize \,\bigg \vert \, \; -\dfrac{4}{12} \\[5pt]
p\cdot \dfrac{5}{12}&=& \dfrac{2}{12} &\quad \scriptsize \,\bigg \vert \, \; \cdot 12 \\[5pt]
p\cdot 5&=& 2 &\quad \scriptsize \,\bigg \vert \, \; :5 \\[5pt]
p&=& 0,4
\end{array}\)](https://mathjax.schullv.de/a07940bbb84f571aea531582097f5f41c9b8094d1af8a69659670348c5d0ea02?color=5a5a5a) Vierfeldertafel angeben
Aus dem Baumdiagramm ergibt sich:
Vierfeldertafel angeben
Aus dem Baumdiagramm ergibt sich:



 Eintragen in eine Vierfeldertafel sowie ergänzen der Gesamtanteile liefert:
Eintragen in eine Vierfeldertafel sowie ergänzen der Gesamtanteile liefert:
| Gesamt | |||
|---|---|---|---|
| Gesamt |
Stochastik (Niveau 2)
10
1. Schritt: Wahrscheinlichkeiten bestimmen
 beschreibt die Wahrscheinlichkeit, die Zahl
beschreibt die Wahrscheinlichkeit, die Zahl  zu werfen.
Da die Wahrscheinlichkeit für das Erzielen der Zahl
zu werfen.
Da die Wahrscheinlichkeit für das Erzielen der Zahl  jeweils doppelt so groß ist wie die Wahrscheinlichkeit für das Erzielen der Zahl
jeweils doppelt so groß ist wie die Wahrscheinlichkeit für das Erzielen der Zahl  gilt
gilt  und somit ergibt sich:
und somit ergibt sich:




 Es muss gelten:
Somit sind die Wahrscheinlichkeiten gegeben durch:
Es muss gelten:
Somit sind die Wahrscheinlichkeiten gegeben durch:





 2. Schritt: Erwartungswert der Augensumme berechnen
3. Schritt: Erwartungswert der Summe der erzielten Zahlen bestimmen
Da der Würfel 6300-mal geworfen wird, folgt:
2. Schritt: Erwartungswert der Augensumme berechnen
3. Schritt: Erwartungswert der Summe der erzielten Zahlen bestimmen
Da der Würfel 6300-mal geworfen wird, folgt:
![\(\begin{array}[t]{rll}
E(\text{Summe})&=& 6\,300 \cdot E(X)&\\[5pt]
&=& 6\,300 \cdot \dfrac{107}{21}&\\[5pt]
&=& 32\,100
\end{array}\)](https://mathjax.schullv.de/4f7fd3b497a506d7e1f8b5e2b0490c6fb6cba7dd713769833d185e1a047af6e1?color=5a5a5a) Der Erwartungswert der Summe der erzielten Zahlen bei
Der Erwartungswert der Summe der erzielten Zahlen bei  Würfen beträgt also
Würfen beträgt also 