A1 - Analysis
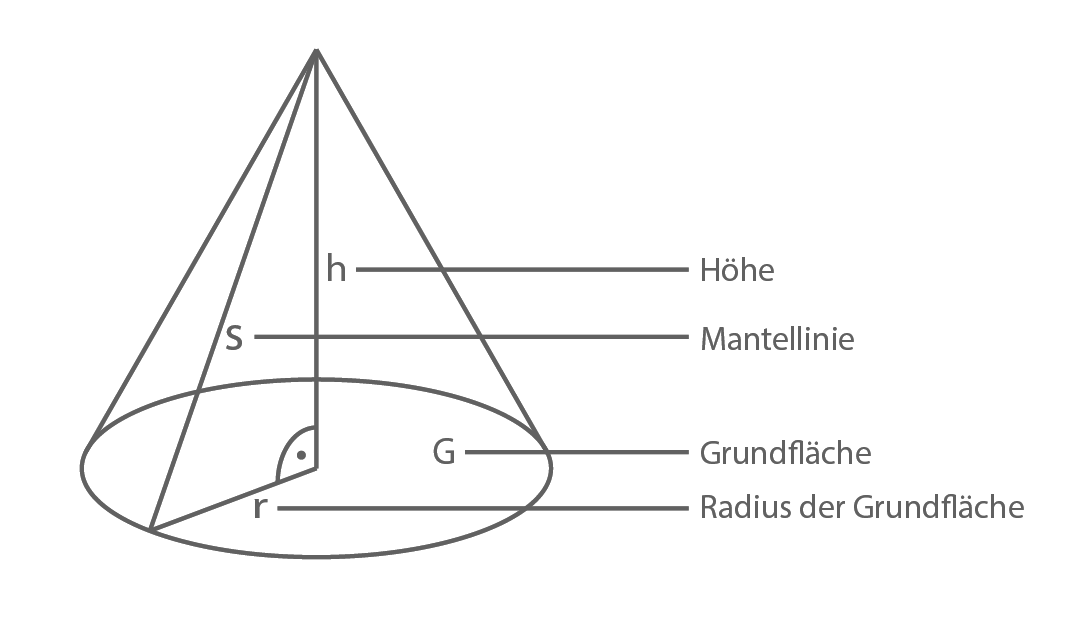
In Material 1 ist ein gerader Kreiskegel dargestellt. Sein Volumen ist abhängig von der Höhe  und der Grundfläche
und der Grundfläche 
 Material 2
Material 2
1.1
Begründe unter Verwendung der Formel
 dass das Volumen auch durch folgende Gleichung bestimmt werden kann, falls die Länge der Mantellinie
dass das Volumen auch durch folgende Gleichung bestimmt werden kann, falls die Länge der Mantellinie  vorgegeben ist:
vorgegeben ist:


(3 BE)
1.2
Bestimme  in Abhängigkeit von
in Abhängigkeit von  so, dass das Volumen des geraden Kreiskegels maximal ist. Gib für diesen Fall sein Volumen und seine Höhe in Abhängigkeit von
so, dass das Volumen des geraden Kreiskegels maximal ist. Gib für diesen Fall sein Volumen und seine Höhe in Abhängigkeit von  an.
an.
(10 BE)
2.
Gegeben sei ein gerader Kreiskegel mit  und
und  Er kann durch die Rotation des Graphen der linearen Funktion
Er kann durch die Rotation des Graphen der linearen Funktion  mit
mit  um die
um die  -Achse im Intervall
-Achse im Intervall ![\(\left[ 0;6\sqrt{2}\right] \)](https://mathjax.schullv.de/370f9706b0fc089cfbd434f891fcfbd832818b1e77ecd0b9ee5b88c4e8a2b631?color=5a5a5a) erzeugt werden.
erzeugt werden.
2.1
Der gerade Kreiskegel soll nun durch Verformungen eine geschwungene Form erhalten. Dazu soll im Intervall ![\(\left[0; 6\sqrt{2}\right]\)](https://mathjax.schullv.de/a6c5814901e1eee12598923be5ef07fc0157d20bc3ad1848f3389533d8da63d2?color=5a5a5a) der Graph einer trigonometrischen Funktion
der Graph einer trigonometrischen Funktion  die geschwungene Form modellieren. Die trigonometrische Funktion
die geschwungene Form modellieren. Die trigonometrische Funktion  besitzt die Funktionsgleichung
und soll folgende Bedingungen erfüllen:
besitzt die Funktionsgleichung
und soll folgende Bedingungen erfüllen:
 und
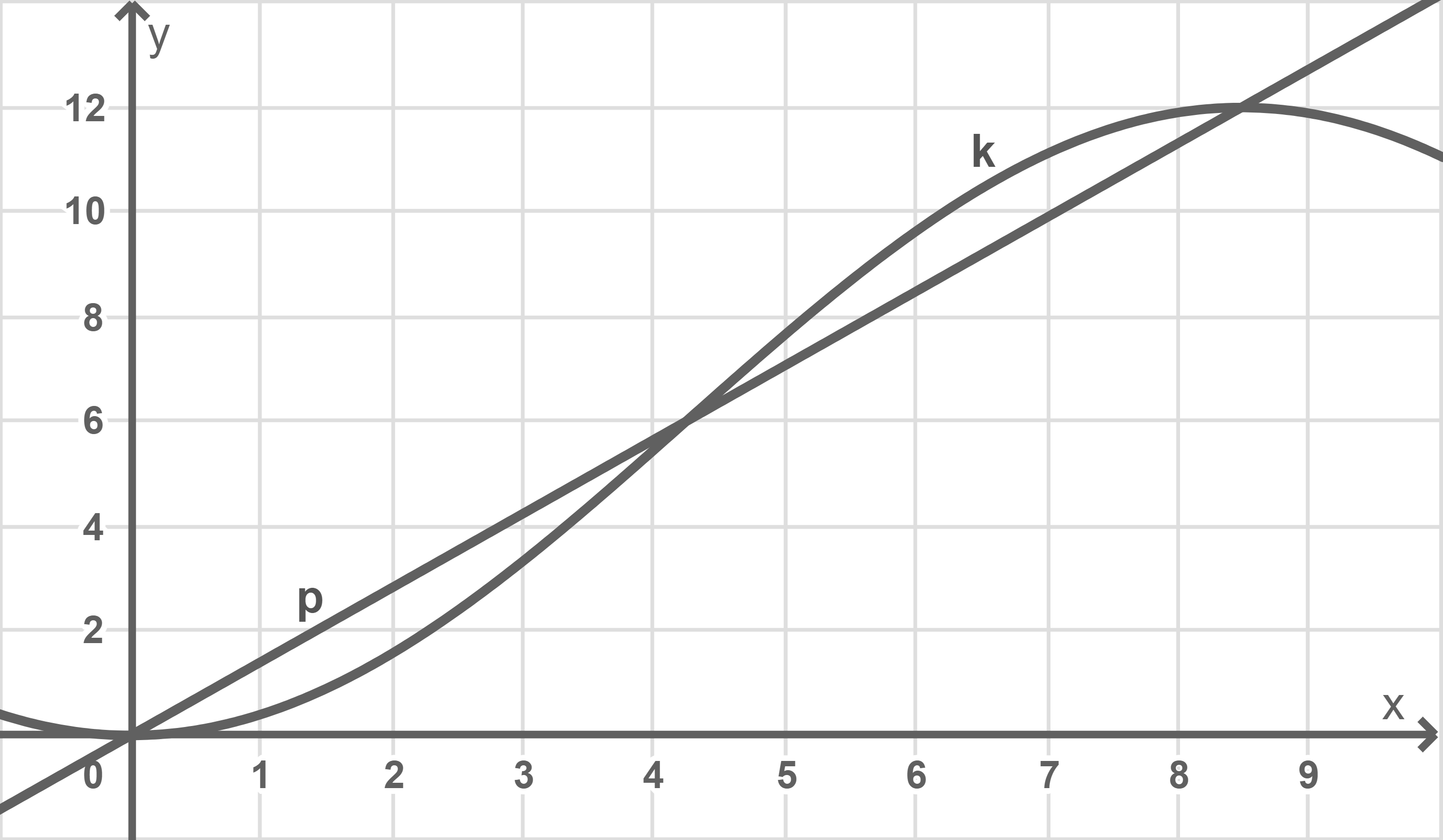
und  sind in Material 2 dargestellt.
sind in Material 2 dargestellt.
Ermittle geeignete Werte für

 und
und  so, dass der Graph von
so, dass der Graph von  die drei genannten Bedingungen erfüllt.
die drei genannten Bedingungen erfüllt.
(1)
Die Periodenlänge beträgt 
(2)
Die Funktionswerte an den Intervallgrenzen des Intervalls stimmen mit denen von  an diesen Stellen überein.
an diesen Stellen überein.
(3)
Der Wertebereich von  umfasst das Intervall
umfasst das Intervall ![\([0;12].\)](https://mathjax.schullv.de/24d7e2faf185629ed359b5769ee46138cb08c8d67cff7c845b1813bff58b4554?color=5a5a5a)
Die Graphen von Ermittle geeignete Werte für
(5 BE)
2.2
Bestimme das Volumen des durch Rotation des Graphen von  um die
um die  -Achse im Intervall
-Achse im Intervall ![\(\left[0;6\sqrt{2}\right]\)](https://mathjax.schullv.de/ca0bef7314e487a545421e55dd6d6caef709ab402f2da36ec47c5ff610fbef53?color=5a5a5a) erzeugten geschwungenen Kegels.
erzeugten geschwungenen Kegels.
Solltest du in Aufgabe 2.1 die Funktion nicht bestimmt haben, verwende stattdessen hier und im Folgenden die Ersatzfunktion
nicht bestimmt haben, verwende stattdessen hier und im Folgenden die Ersatzfunktion  mit
mit
Solltest du in Aufgabe 2.1 die Funktion
(3 BE)
3.
In den Zeilen (1) bis (5) ist ein Verfahren zur Ermittlung des unbestimmten Integrals  angeführt. Erkläre die einzelnen Umformungsschritte:
angeführt. Erkläre die einzelnen Umformungsschritte:
(9 BE)
4.
Werden die durch Rotation der Graphen von  und
und  aus Aufgabe 2 um die
aus Aufgabe 2 um die  -Achse im Intervall
-Achse im Intervall ![\(\left[0;6\sqrt{2} \right]\)](https://mathjax.schullv.de/203c85bc16d8a9ba0602d412892e4a0906d0bb2b3d130784457dda0afb40ebf1?color=5a5a5a) erzeugten Körper auf die Spitze gestellt und sind damit nach oben geöffnet, können sie als Gefäße aufgefasst werden. Sie sollen jeweils mit Wasser gefüllt werden. Das Wasser strömt in die Gefäße mit einer gleichmäßigen Geschwindigkeit von
erzeugten Körper auf die Spitze gestellt und sind damit nach oben geöffnet, können sie als Gefäße aufgefasst werden. Sie sollen jeweils mit Wasser gefüllt werden. Das Wasser strömt in die Gefäße mit einer gleichmäßigen Geschwindigkeit von  pro Sekunde ein. Die Funktion
pro Sekunde ein. Die Funktion  soll die Füllhöhe (in
soll die Füllhöhe (in  ) in dem durch Rotation des Graphen von
) in dem durch Rotation des Graphen von  erzeugten Gefäßes in Abhängigkeit von der Zeit
erzeugten Gefäßes in Abhängigkeit von der Zeit  (in Sekunden) beschreiben. Die Funktion
(in Sekunden) beschreiben. Die Funktion  soll die Füllhöhe in dem durch die Rotation des Graphen von
soll die Füllhöhe in dem durch die Rotation des Graphen von  erzeugten Gefäßes in Abhängigkeit von der Zeit
erzeugten Gefäßes in Abhängigkeit von der Zeit  (in Sekunden) beschreiben.
(in Sekunden) beschreiben.
4.1
Zeige unter Benutzung eines CAS, dass  gilt.
gilt.
(5 BE)
4.2
Ermittle den Funktionsterm 
Material 1
(5 BE)

Abb. 1

Abb. 2
1.1
Der Radius  die Mantellinie
die Mantellinie  und die Höhe
und die Höhe  des Kegels bilden gemeinsam ein rechtwinkliges Dreieck. Mit dem Satz des Pythagoras folgt:
Mit dieser Darstellung der Höhe und der Formel für den Flächeninhalt der kreisförmigen Grundfläche
des Kegels bilden gemeinsam ein rechtwinkliges Dreieck. Mit dem Satz des Pythagoras folgt:
Mit dieser Darstellung der Höhe und der Formel für den Flächeninhalt der kreisförmigen Grundfläche  folgt:
folgt:
1.2
Radius für maximales Volumen bestimmen
1. Schritt: (Ableitungs)funktionen im CAS definieren
 Abb. 1: Definieren der Ableitungen
2. Schritt: Notwendiges Kriterium für Extremalstellen anwenden
Anwendung des notwendigen Kriteriums und umformen nach
Abb. 1: Definieren der Ableitungen
2. Schritt: Notwendiges Kriterium für Extremalstellen anwenden
Anwendung des notwendigen Kriteriums und umformen nach  liefert das Ergebnis:
liefert das Ergebnis:
 Abb. 2: Gleichung lösen mit dem CAS
3. Schritt: Hinreichendes Kriterium für Extremalstellen anwenden
Durch Anwendung des hinreichenden Kriteriums für Extremalstellen folgt:
Abb. 2: Gleichung lösen mit dem CAS
3. Schritt: Hinreichendes Kriterium für Extremalstellen anwenden
Durch Anwendung des hinreichenden Kriteriums für Extremalstellen folgt:
 Abb. 3: Überprüfen mit dem CAS
Das maximale Volumen nimmt der Kreiskegel damit für
Abb. 3: Überprüfen mit dem CAS
Das maximale Volumen nimmt der Kreiskegel damit für  an.
4. Schritt: Volumen und Höhe bestimmen
Mit Hilfe des CAS ergibt sich:
Das maximale Volumen des Kegels beträgt somit
an.
4. Schritt: Volumen und Höhe bestimmen
Mit Hilfe des CAS ergibt sich:
Das maximale Volumen des Kegels beträgt somit  und wird für
und wird für  und
und  angenommen.
angenommen.
Der Befehl für eine Ableitung befinden sich im Taschenrechner am folgenden Ort:
Keyboard  Math2
Math2
 Abb. 1: Definieren der Ableitungen
Abb. 1: Definieren der Ableitungen
Dazu wird der solve-Befehl des CAS auf  angewendet. Nach Beachtung, dass
angewendet. Nach Beachtung, dass  sein müssen, liefert der CAS folgende Ergebnisse:
sein müssen, liefert der CAS folgende Ergebnisse:
 und
und 
 Abb. 2: Gleichung lösen mit dem CAS
Abb. 2: Gleichung lösen mit dem CAS
 Abb. 3: Überprüfen mit dem CAS
Abb. 3: Überprüfen mit dem CAS
2.1
Werte ermitteln
Vergleich der allgemeinen Sinusfunktion 
 mit
mit 
 liefert:
Periodenlänge
liefert:
Periodenlänge  Der Wertebereich beträgt
Der Wertebereich beträgt ![\([0;12],\)](https://mathjax.schullv.de/55153c4169e7fb2398aefcd0fdc535b8b836db907926d807705dcd677a60cef5?color=5a5a5a) die Amplitude von
die Amplitude von  , allgemein durch
, allgemein durch  ausgedrückt, beträgt damit
ausgedrückt, beträgt damit 
Berechnung der restlichen Werte:![\(\begin{array}[t]{rll}
\dfrac{2\pi}{\dfrac{2\cdot \pi}{L}} &=& 12\sqrt{2} \\[5pt]
2\pi \cdot \dfrac{L}{2\pi}&=& 12\sqrt{2} \\[5pt]
L&=& 12\sqrt{2}
\end{array}\)](https://mathjax.schullv.de/1f99b2e0e14e882090e646cf2b2482c9dd26e3f22516bd620ae7a1a52cc72209?color=5a5a5a) Zusammen mit
Zusammen mit  folgt:
Da der Wertebereich von
folgt:
Da der Wertebereich von  durch das Intervall
durch das Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) gegeben ist, muss der Graph um sechs Einheiten in positive
gegeben ist, muss der Graph um sechs Einheiten in positive  -Richtung verschoben werden, es folgt
-Richtung verschoben werden, es folgt  Mit Hilfe von
Mit Hilfe von  wird nun
wird nun  bestimmt:
Es gilt somit insgesamt:
bestimmt:
Es gilt somit insgesamt:


 und
und 
Berechnung der restlichen Werte:
2.2
Volumen berechnen
Das für das Volumen eines Rotationskörpers benötigte Integral wird im CAS wie folgt aufgerufen:
 Abb. 4: Berechnung mit dem CAS
Das Volumen des durch Rotation des Graphen von
Abb. 4: Berechnung mit dem CAS
Das Volumen des durch Rotation des Graphen von  um die
um die  -Achse erzeugten geschwungenen Kegels beträgt ca.
-Achse erzeugten geschwungenen Kegels beträgt ca. 
Keyboard  Math2
Es folgt:
Math2
Es folgt:
![\(\begin{array}[t]{rll}
V&=& \pi \cdot \displaystyle\int_{0}^{6\sqrt{2}}\left(k(x)\right)^2\;\mathrm dx \\[5pt]
&\approx& 1439,49 \; \text{[cm}^2]
\end{array}\)](https://mathjax.schullv.de/be66e2a28abe6d6f9760d6c628f2881cf991bb6495da86de85d11d44be19dcd2?color=5a5a5a)
 Abb. 4: Berechnung mit dem CAS
Abb. 4: Berechnung mit dem CAS
3.
Umformungsschritte erklären
(1)
Das Quadrat des Sinus wird als Multiplikation geschrieben.
(2)
Partielle Integration wird auf das Produkt angewendet.
(3)
Zunächst wird der Faktor  vor das Integral gezogen:
Anschließend wird folgender trigonometrischer Zusammenhang verwendet:
Insgesamt folgt damit:
vor das Integral gezogen:
Anschließend wird folgender trigonometrischer Zusammenhang verwendet:
Insgesamt folgt damit:
(4)
Zunächst wird auf der rechten Seite der Gleichung das Integral in zwei Integrale aufgeteilt und das Vordere berechnet:
Durch Betrachtung der ganzen Gleichung und Addition des rechten Integrals folgt dann:
(5)
Schlussendlich wird die Gleichung durch zwei dividiert und die Integrationskonstante  zu
zu  umbenannt.
umbenannt.
4.1
Wert nachweisen
Pro Sekunde fließen  Wasser in das Gefäß. Nach drei Sekunden befinden sich damit
Wasser in das Gefäß. Nach drei Sekunden befinden sich damit  Wasser im Gefäß.
Wasser im Gefäß.
 Abb. 5: Lösen mit dem CAS
Abb. 5: Lösen mit dem CAS
Die Berechnung der Höhe  sodass das Rotationsvolumen über
sodass das Rotationsvolumen über  im Intervall
im Intervall ![\([0;h_K]\)](https://mathjax.schullv.de/8a2b0d9d3df21f1acb984d5b646531cfe5039066e1fc64c271ae2069b207c700?color=5a5a5a) den Wert
den Wert  ergibt, liefert mit dem solve-Befehl des CAS:
ergibt, liefert mit dem solve-Befehl des CAS:
 Abb. 5: Lösen mit dem CAS
Abb. 5: Lösen mit dem CAS
4.2
Funktionsterm ermitteln
1. Schritt: Term für das Volumen des Gefäßes bestimmen
Mit der Volumenformel für einen Kreiskegel folgt:
2. Schritt: Term für das eingeflossene Wasservolumen bestimmen
Es folgt in Abhängigkeit von  in Sekunden:
in Sekunden:
 3. Schritt: Gleichung aufstellen
Gleichsetzen liefert:
Die Füllhöhe des Gefäßes kann somit in Abhängigkeit von
3. Schritt: Gleichung aufstellen
Gleichsetzen liefert:
Die Füllhöhe des Gefäßes kann somit in Abhängigkeit von  durch folgende Funktion beschrieben werden:
durch folgende Funktion beschrieben werden:
![\(h_p(t)=3\cdot \sqrt[3]{t} \)](https://mathjax.schullv.de/5898c33d3386da34bd79a20aba93c78f051e87ab3e518a4b41005803456cb420?color=5a5a5a)