C2.2 - Stochastik

Die Grafiken im Material zeigen für das Jahr $2017$ eine Übersicht des Statistischen Bundesamtes über die neu abgeschlossenen Ausbildungsverträge nach schulischer Vorbildung, aufgeteilt nach Geschlecht.

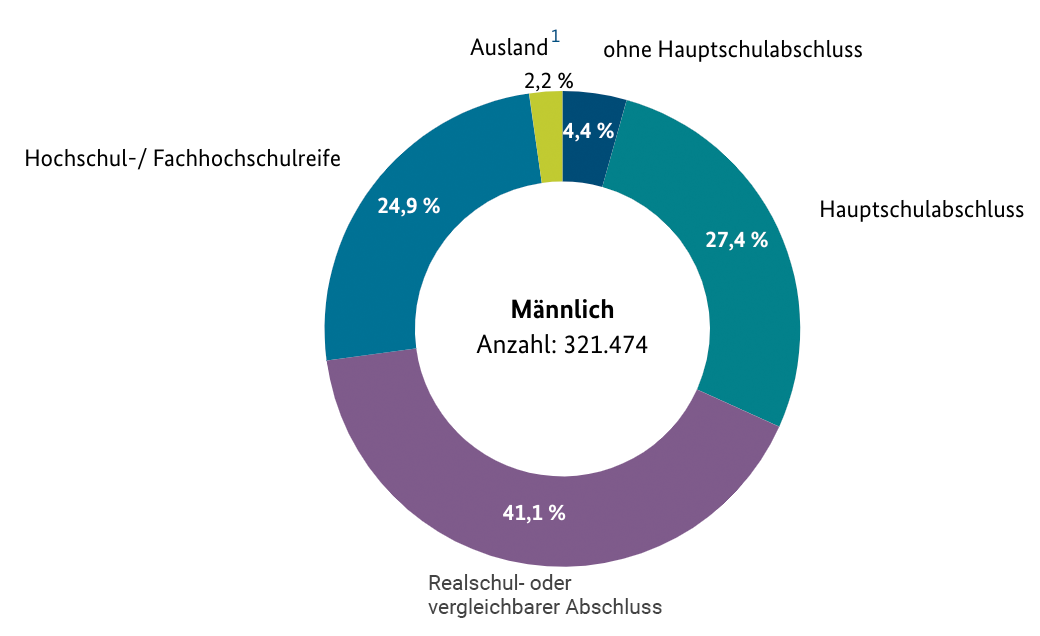
Kreisdiagramm zeigt die Verteilung männlicher Abschlüsse in Prozent. Insgesamt 321.474 Personen.

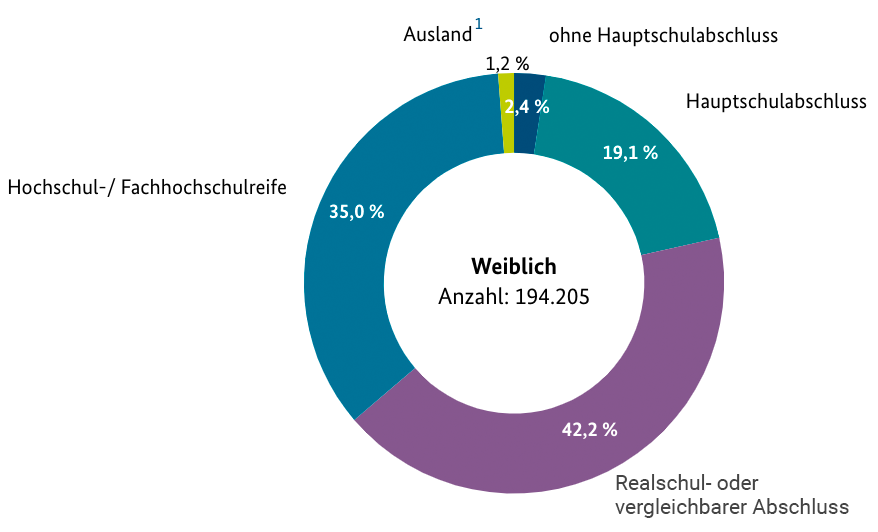
Kreisdiagramm zur Verteilung weiblicher Schulabschlüsse in Deutschland.

¹ Im Ausland erworbener Schulabschluss, der nicht zugeordnet werden kann.

Material 1: Im Jahr 2017 neu abgeschlossene Ausbildungsverträge nach schulischer Vorbildung (insgesamt 515 679) – aufgeteilt nach Geschlecht (männlich/weiblich) ^[1]

1.1

Gib mithilfe der Daten aus dem Material die sinnvoll gerundeten absoluten Häufigkeiten in der folgenden Tabelle an. Die Bezeichnungen der Merkmale lauten:

$H:$ Hochschul-/Fachhochschulreife,
$W:$ weiblich

$\overline{H}:$ keine Hochschul-/Fachhochschulreife
$\overline{W}:$ nicht weiblich

	$\color{#fff}{W}$	$\color{#fff}{\overline{W}}$	$\color{#fff}{\Sigma}$
$H$
$\overline{H}$
$\Sigma$

(4 BE)

Im Folgenden sollen mithilfe der in der Tabelle angegebenen absoluten Häufigkeiten Wahrscheinlichkeiten berechnet werden. Es werden ausschließlich Personen betrachtet, die $2017$ einen Ausbildungsvertrag neu abgeschlossen haben.

1.2

Eine Personalleiterin lädt $2017$ eine zufällig ausgewählte Person mit Hochschul-/Fachhochschulreife zu einem Vorstellungsgespräch ein.
Ermittle die Wahrscheinlichkeit, dass diese Person nicht weiblich ist.

(3 BE)

1.3

Bestimme die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person weiblich ist oder eine Hochschul-/Fachhochschulreife besitzt.

(3 BE)

1.4

Untersuche, ob die Wahrscheinlichkeiten $P_\overline{H}(W)$ und $P(W)$ übereinstimmen. Deute dein Ergebnis im Sachzusammenhang.

(3 BE)

Eine Personalleiterin hat $50$ Personen mit Hochschul-/Fachhochschulreife zu einem Auswahlverfahren eingeladen. Von den $50$ Personen sind $30$ weiblich.

1.5

Für eine Gruppendiskussion werden $5$ von den $50$ Personen zufällig ausgewählt. Bestimme die Wahrscheinlichkeit, dass sich darunter $4$ weibliche Personen befinden.

(3 BE)

1.6

Im Rahmen des Auswahlverfahrens wird ein Multiple-Choice Test durchgeführt. Bei diesem Test werden genau acht Fragen gestellt. Zu jeder der Fragen gibt es vier Antwortmöglichkeiten, von denen jeweils genau eine richtig ist. Bestimme die Wahrscheinlichkeit, dass man durch bloßes Raten genau $7$ Fragen richtig beantwortet.

(2 BE)

1.7

In einem weiteren Teil des Auswahlverfahrens stehen verschiedene Aufgaben in einem Pool zur Verfügung. Der Bewerber oder die Bewerberin zieht zwei Aufgaben aus diesem Pool, die dann zu bearbeiten sind. Dabei gibt es $435$ Kombinationsmöglichkeiten. Berechne die Anzahl der Aufgaben, die sich im Pool befinden.

(5 BE)

Im Folgenden sollen die in den Grafiken im Material angegebenen relativen Häufigkeiten als Wahrscheinlichkeiten betrachtet werden.

Es werden nur die im Jahr $2017$ neu abgeschlossenen Ausbildungsverträge von männlichen Personen betrachtet.

2.1

Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse $A, B$ und $C$ unter Angabe der jeweils verwendeten Zufallsgröße. Gehe davon aus, dass die Zufallsgrößen binomialverteilt sind.

$A:$ $4$ von $15$ zufällig ausgewählten neu abgeschlossenen Ausbildungsverträgen werden von Männern mit Hauptschulabschluss abgeschlossen.

$B:$ Weniger als $50$ von $100$ zufällig ausgewählten neu abgeschlossenen Ausbildungsverträgen werden von Männern mit einem Realschul- oder vergleichbaren Abschluss abgeschlossen.

$C:$ Mindestens $142$ aber höchstens $153$ von $200$ zufällig ausgewählten neu abgeschlossenen Ausbildungsverträgen werden von Männern abgeschlossen, die weder eine Hochschul-/Fachhochschulreife besitzen noch einen Abschluss im Ausland erworben haben.

(8 BE)

2.2

Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term $1-(0,249^{10}+0,751^{10})$ berechnet werden kann.
Gib dieses Ereignis an.

(3 BE)

2.3

In einer Umfrage werden Männer, die $2017$ einen Ausbildungsvertrag neu abgeschlossen haben, zufällig ausgewählt und nach ihrer schulischen Vorbildung befragt. Berechne, wie viele Männer man mindestens befragen muss, um mit einer Wahrscheinlichkeit von mindestens $80 \,\%$ auf mindestens einen Mann mit Hauptschulabschluss zu treffen.

(4 BE)

Von den Auszubildenden, die $2017$ einen Ausbildungsvertrag neu abgeschlossen haben und die Hochschul-/Fachhochschulreife erworben hatten, haben $34,9 \,\%$ einen Ausbildungsvertrag im Bereich Industrie und Handel abgeschlossen.

Da der Anteil der Ausbildungsverträge im Bereich Industrie und Handel seit Jahren steigt, wird vermutet, dass im Jahr $2020$ der Anteil der Auszubildenden, welche die Hochschul-/Fachhochschulreife erworben und einen Ausbildungsvertrag im Bereich Industrie und Handel abgeschlossen haben, bereits größer als $40 \,\%$ ist.
Um diese Vermutung zu bestätigen, werden $150$ zufällig ausgewählte Auszubildende mit der schulischen Vorbildung Hochschul-/Fachhochschulreife befragt, die $2020$ einen neuen Ausbildungsvertrag abgeschlossen haben.

3.1

Entwickle einen Hypothesentest auf einem Signifikanzniveau von $10 \,\%$ und formuliere eine Entscheidungsregel im Sachzusammenhang.

(7 BE)

3.2

Beschreibe für den Hypothesentest aus Aufgabe 3.1 die Bedeutung des Fehlers 2. Art im Sachzusammenhang.
Bei diesem Hypothesentest soll die Wahrscheinlichkeit für einen Fehler 2. Art höchstens dreimal so groß sein wie das Signifikanzniveau $\alpha.$ Ermittle auf drei Nachkommastellen genau, wie hoch der zur Alternativhypothese $H_1$ gehörige tatsächliche Anteil $p_1$ unter dieser Bedingung mindestens sein müsste.

(5 BE)

^[1] basierend auf: Statistisches Bundesamt, Fachserie 11 Reihe 3; Deutsches Zentrum für Hochschul- und Wissenschaftsforschung, Berechnungen, Interaktive Grafik 2.4.34, URL: https://www.datenportal.bmbf.de/portal/de/grafik-2.4.34.html (abgerufen am 04.01.2021).

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

	$\color{#fff}{W}$	$\color{#fff}{\overline{W}}$	$\color{#fff}{\Sigma}$
$H$	$67\,972$	$80\,047$	$148\,019$
$\overline{H}$	$126\,233$	$241\,427$	$367\,660$
$\Sigma$	$194\,205$	$321\,474$	$515\,679$

1.2

$P_H(\overline{W})= \dfrac{P(\overline{W}\cap H)}{P(H)}=\dfrac{80\,047}{148\,019} \approx 0,5408$

Die Wahrscheinlichkeit, dass die Person nicht weiblich ist, beträgt etwa $54,08 \%.$

1.3

$P(W)+P(H)-P(W \cap H)$ $= \dfrac{194\,205 + 148\,019-67\,972}{515\,679}$ $\approx 0,532$

Die Wahrscheinlichkeit , dass die Person weiblich ist oder eine Hochschul-/Fachhochschulreife besitzt, beträgt etwa $53,2 \; \%$ .

1.4

$P(W) = \dfrac{194\,205}{515\,679} \approx 0,3766$

$P_{\overline{H}}(W) = \dfrac{P(W\cap \overline{H})}{P(\overline{H})}= \dfrac{\frac{126\,233}{515\,679}}{\frac{367\,660}{515\,679}} \approx 0,3433$

Die Wahrscheinlichkeiten stimmen nicht überein.
Im Sachzusammenhang: Die Merkmale "hat keine Hochschul-/Fachhochschulreife" und "ist weiblich" sind stochastisch abhängig voneinander.

1.5

Es gibt fünf Möglichkeiten, wie die weiblichen Personen ausgewählt werden. Damit folgt:

$5 \cdot \dfrac{30}{50} \cdot \dfrac{29}{49} \cdot \dfrac{28}{48} \cdot \dfrac{27}{47} \cdot \dfrac{20}{46}$ $\approx 0,2587$

Die Wahrscheinlichkeit, dass sich unter $5$ zufällig ausgewählten Personen $4$ weibliche Personen befinden, beträgt etwa $25,87 \%$ .

1.6

Die Zufallsvariable $X$ beschreibt die Anzahl richtig geratener Fragen.

$X$ ist $B_{8; \; 0,25}$ -verteilt.

Mit dem Taschenrechner folgt:

$P(X = 7) \approx 0,0004$

Die Wahrscheinlichkeit, durch Raten $7$ der $8$ Fragen richtig zu beantworten, liegt bei etwa $0,04 \%$ .

1.7

Sei $n$ die Menge verfügbarer Aufgaben und $k = 2$ die Anzahl der gezogenen Aufgaben.

Es handelt sich um Ziehen ohne Zurücklegen und ohne Reihenfolge. Mit der entsprechenden Kombinationsformel folgt:

Vollständigen Rechenweg anzeigen

$0=n^2-n-870$

Durch Anwenden der pq-Formel folgt:

$\begin{array}[t]{rll} n_{1,2}&=&\dfrac{1}{2}\pm \sqrt{\left(\dfrac{1}{2}\right)^2-(-870)} & \\[5pt] \end{array}$

$n_1 = 30 \qquad n_2 = -29$

Im Sachzusammenhang ergibt $n_2 =-29$ keinen Sinn.

Daher befinden sich $30$ verschiedene Aufgaben im Pool.

2.1

Ereignis A

Die Zufallsvariable $X$ beschreibt die Anzahl an Männern mit Hauptschulabschluss.

$X$ ist $B_{15; \; 0,274}$ -verteilt.

$P(A) = P(X = 4) \approx 0,2272$

Ereignis B

Die Zufallsvariable $Y$ beschreibt die Anzahl an Männern mit Realschul- oder vergleichbaren Abschluss.

$Y$ ist $B_{100; \; 0,411}$ -verteilt.

$P(B) = P(X \leq 49) \approx 0,9553$

Ereignis C

Die Zufallsvariable $Z$ beschreibt die Anzahl an Männern, die weder eine Hochschul-/ Fachhochschulreife besitzen, noch einen Abschluss im Ausland erworben haben.

$Z$ ist $B_{200; \; 1-(0,249 + 0,022)} = B_{200; \; 0,729}$ -verteilt.

$P(C) = P(142 \leq Z \leq 153)$ $= P(Z \leq 153) - P(Z \leq 141)$ $\approx 0,646$

2.2

Zufallsexperiment beschreiben

10 zufällig ausgewählte männliche Personen werden befragt, ob sie eine Hochschul-/Fachhochschulreife haben.

Ereignis angeben

Von den 10 zufällig gewählten männlichen Personen besitzen nicht alle 10 eine Hochschul-/Fachhochschulreife, jedoch auch nicht alle 10 keine Hochschul-/Fachhochschulreife.

Es besitzen folglich mindestens eine und höchstens neun befragte Personen eine Hochschul-/Fachhochschulreife.

Die Wahrscheinlichkeit für das Ereignis beträgt etwa $94,29 \%$ .

2.3

Sei $X$ die Anzahl von Männern mit Hauptschulabschluss.

$X$ ist $B_{n; \; 0,274}$ verteilt.

Gesucht ist die kleinste natürliche Zahl $n$ , sodass Folgendes gilt:

$\begin{array}[t]{rll} P(X \geq 1)& \geq& 0,8& \quad \scriptsize \\[5pt] P(X = 0)& \leq& 0,2& \end{array}$

Durch systematisches Ausprobieren mit dem Taschenrechner folgt:

$n = 5: \quad P(X=0) \approx 0,2017$
$n = 6: \quad P(X=0) \approx 0,1464$

Es müssen folglich mindestens $6$ Männer befragt werden, um mit einer Wahrscheinlichkeit von mindestens $80 \%$ auf mindestens einen Mann mit Hauptschulabschluss zu treffen.

3.1

Es wird ein rechtsseitiger Hypothesentest durchgeführt:

$H_0: p \leq 0,4 \qquad H_1: p \gt 0,4 \qquad$ $\alpha = 0,1$

Die Zufallsvariable $X$ beschreibt die Anzahl der Auszubildenden, die mit einer Hochschul-/Fachhochschulreife einen Ausbildungsvertrag im Bereich Industrie und Handel abgeschlossen haben. $X$ ist im Extremfall $B_{150; \; 0,4}$ -verteilt.

Der Ablehnungsbereich wird durch $A = \{g; g+1; \dots; 150 \}$ beschrieben.

Gesucht ist die kleinste natürlich Zahl $g$ , sodass Folgendes gilt:

$\begin{array}[t]{rll} P(X \geq g)& \leq& 0,1& \quad \scriptsize \\[5pt] P(X \leq g-1)& \geq& 0,9 \end{array}$

Durch systematisches Ausprobieren mit dem Taschenrechner folgt:

$P(X \leq 67) \approx 0,8937$
$P(X \leq 68) \approx 0,9210$

Damit gilt für den Ablehnungsbereich: $A = \{69; \dots ; 150 \}$ .

Entscheidungsregel
Wenn mindestens $69$ Auszubildende einen Ausbildungsvertrag im Bereich Industrie und Handel abgeschlossen haben, wird die Nullhypothese abgelehnt. Andernfalls wird sie nicht abgelehnt.

3.2

Fehler 2. Art im Sachzusammenhang

Obwohl mindestens $69$ Auszubildende einen Ausbildungsvertrag im Bereich Industrie und Handel abgeschlossen haben, wird im Hypothesentest die Nullhypothese nicht abgelehnt.

Anteil $p_1$ berechnen

Aus der Entscheidungsregel ergibt sich folgender Annahmebereich für $H_0: A =\{0; \dots; 68 \}.$ Die Wahrscheinlichkeit für den Fehler $2.$ Art soll dabei maximal $30 \%$ betragen.

Für $n = 150$ muss also gelten:

$\begin{array}[t]{rll} P(X \leq 68)& \leq& 0,3&\quad \scriptsize \\[5pt] \end{array}$

Durch systematisches Ausprobieren mit dem Taschenrechner folgt:

$p = 0,478: P(X\leq 68) \approx 0,3008$
$p = 0,479: P(X\leq 68) \approx 0,2924$

Der zur Alternativhypothese $H_1$ gehörige Anteil $p_1$ müsste in Wirklichkeit mindestens $47,9 \%$ betragen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?