C2 - Stochastik

Die Speisekarte in Material 1 zeigt die angebotenen Speisen einer Mitarbeiter-Kantine an einem Freitag. Man kann sich täglich ein Drei-Gänge-Menü zusammenstellen, indem man eine Vorspeise, eine Hauptspeise und ein Dessert auswählt. Die Gäste haben nach ihrer Auswahl alle Speisen auf einem Tablett, so dass die Reihenfolge der Auswahl keine Rolle spielt.

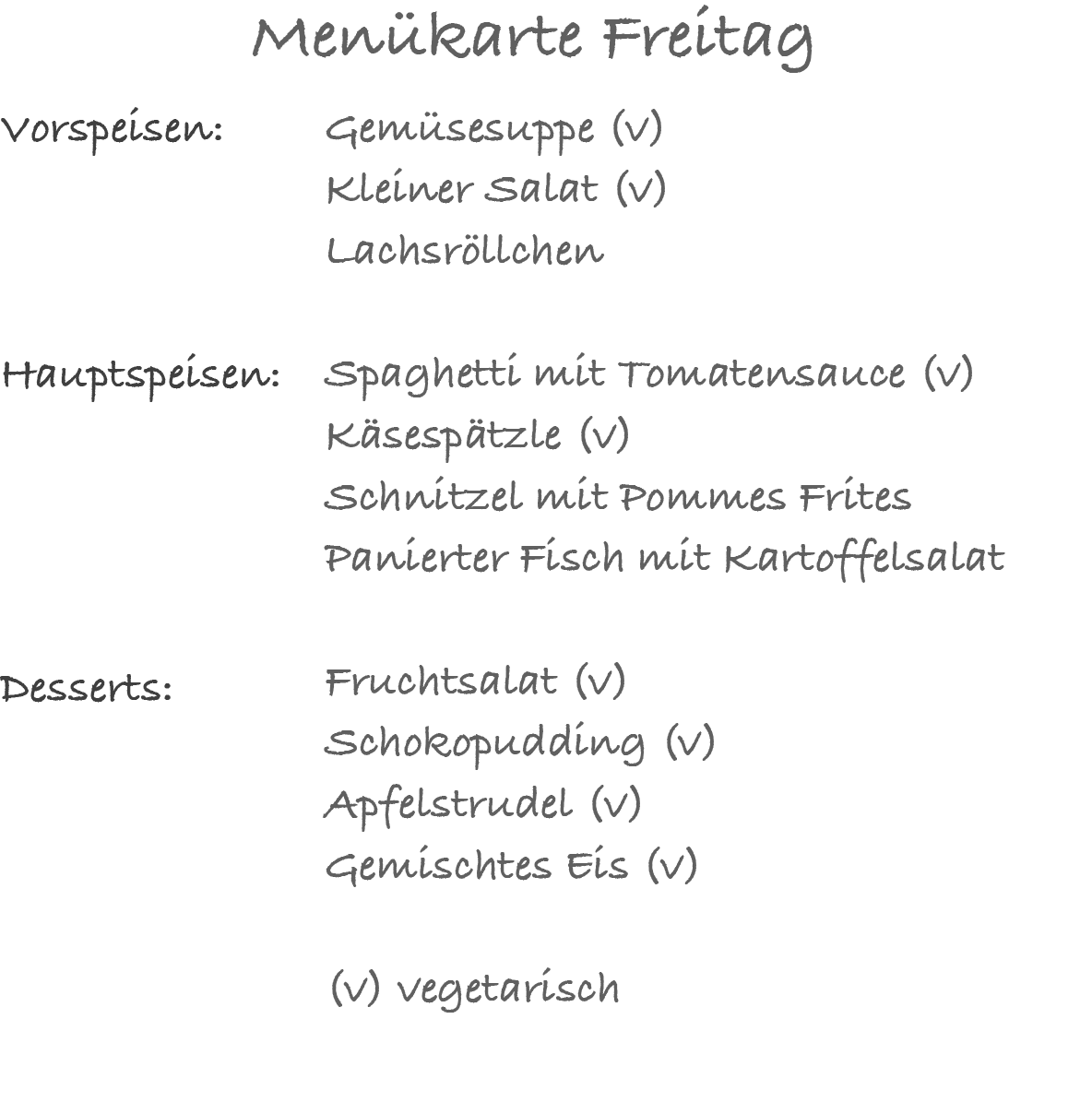
Material 1

Berechne die Anzahl

$N_1$

aller möglichen Menüs,

$N_2$

der möglichen Menüs, wenn man die Hauptspeise durch eine Vorspeise ersetzt (die beiden so gewählten Vorspeisen sollen unterschiedlich sein),

$N_3$

der möglichen vegetarischen Menüs, wenn entweder eine Vorspeise, eine Hauptspeise und ein Dessert oder zwei unterschiedliche Vorspeisen und eine Hauptspeise gewählt werden.

(3 BE)

Die folgenden Anteile beziehen sich auf die Gesamtheit der Besucher der Kantine. Der Anteil der Vegetarier beträgt $30 \;\%$ . Alle in Material 1 genannten Vorspeisen und alle Desserts sind gleich beliebt. Bei den Hauptspeisen wählen $20 \;\%$ die Spaghetti, $25\; \%$ die Käsespätzle, $35 \;\%$ das Schnitzel und der Rest den Fisch. Es werden im Folgenden nur die Personen betrachtet, die aus jedem Gang eine Speise wählen. Vegetarier wählen ausschließlich aus den mit (v) gekennzeichneten Gerichten. Die Kantine wird täglich von mehr als 1000 Personen besucht.

2.1

Erläutere allgemein, unter welchen Bedingungen man bei der Bestimmung von Wahrscheinlichkeiten von Bernoulliketten ausgehen kann.

(2 BE)

2.2

Bestimme unter der Voraussetzung, dass es sich jeweils um eine Bernoullikette handelt, die Wahrscheinlichkeiten der folgenden Ereignisse:

$A:$

Von 10 zufällig ausgewählten Besuchern der Kantine sind genau 4 Vegetarier.

$B:$

Von 50 zufällig ausgewählten Besuchern der Kantine wählen höchstens 8 die Spaghetti.

$C:$

Von 100 zufällig ausgewählten Besuchern der Kantine wählen mindestens 30 und höchstens 40 das Schnitzel.

$D:$

Von 20 zufällig ausgewählten Besuchern der Kantine wählen die ersten vier die Lachsröllchen, von den restlichen 16 Besuchern wählen fünf den kleinen Salat.

(10 BE)

2.3

Die beiden vegetarischen Hauptspeisen sind bei den Vegetariern gleich beliebt. Betrachtet werden die Merkmale $V$ : Besucher ist Vegetarier und $K$ : Besucher wählt Käsespätzle.

2.3.1

Bestimme die Wahrscheinlichkeiten der folgenden Ereignisse:

$E:$

Ein zufällig ausgewählter Besucher ist Vegetarier und wählt nicht die Käsespätzle.

$F:$

Ein zufällig ausgewählter Besucher, der die Käsespätzle gewählt hat, ist Vegetarier.

$G:$

Ein zufällig ausgewählter Besucher, der kein Vegetarier ist, entscheidet sich für die Käsespätzle.

(9 BE)

2.3.2

Untersuche die Merkmale $V$ und $K$ auf stochastische Unabhängigkeit.

(3 BE)

Der Betreiber der Kantine hat die Vermutung, dass der Anteil der Vegetarier nicht mehr $30\; \%$ beträgt, sondern gestiegen sein könnte, da die vegetarischen Gerichte stärker nachgefragt werden. Um das Angebot gegebenenfalls anpassen zu können, werden 150 zufällig ausgewählte Besucher der Kantine gefragt, ob sie Vegetarier sind. Bei der Befragung geben 57 Personen an, Vegetarier zu sein.

3.1

Entwickle anhand der Angaben einen Hypothesentest mit einem Signifikanzniveau von $5\; \%$ und formuliere eine Entscheidungsregel im Sachzusammenhang.
Entscheide, ob davon auszugehen ist, dass der Anteil der Vegetarier gestiegen ist.

(7 BE)

3.2

Erläutere die Fehler 1. und 2. Art und deren mögliche Konsequenzen im Sachzusammenhang.

(4 BE)

3.3

Bestimme die Wahrscheinlichkeit für einen Fehler 2. Art, wenn sich der Anteil der Vegetarier tatsächlich auf $40 \%$ erhöht hat.

(3 BE)

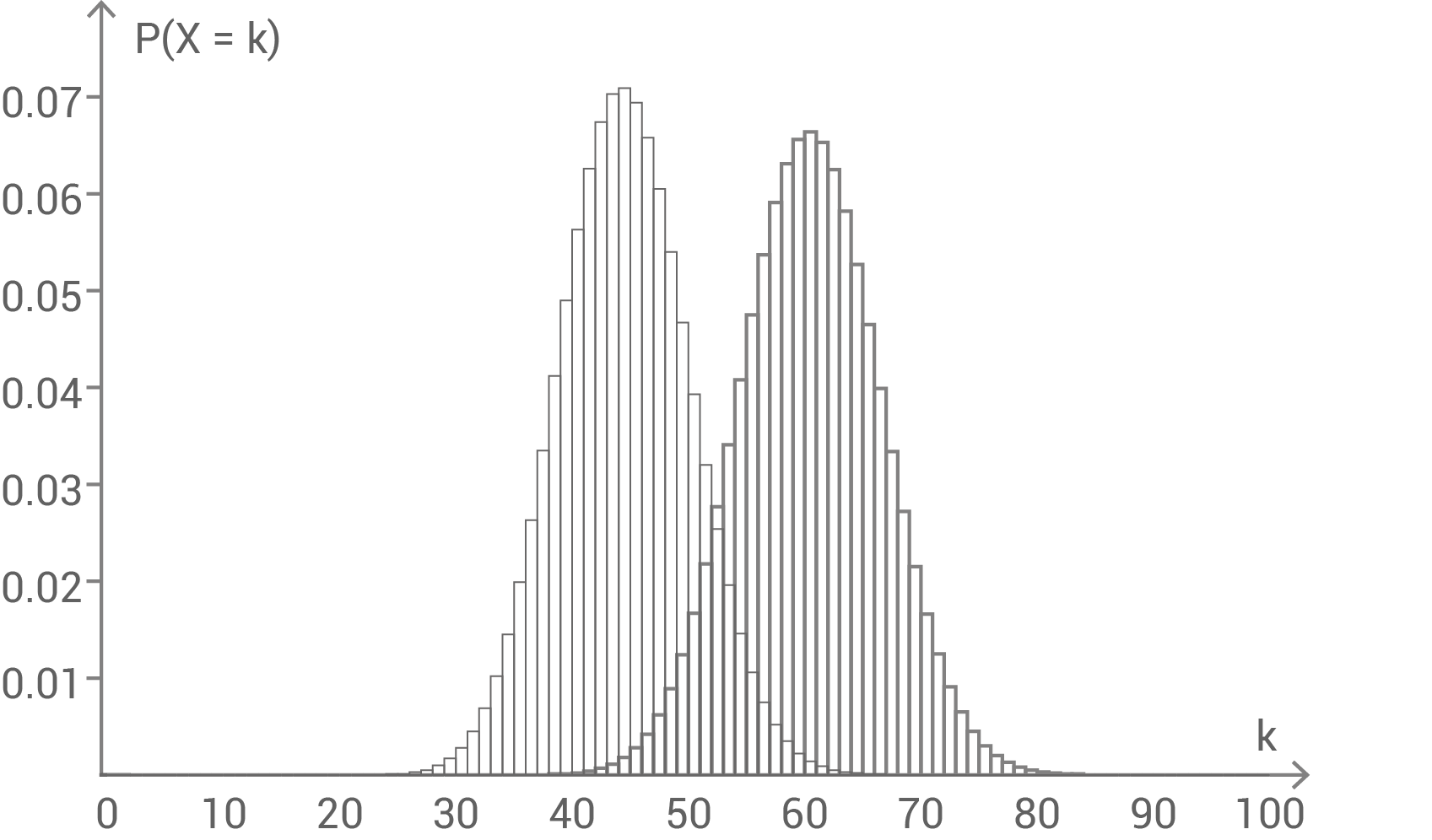
3.4

In Material 2 sind die Wahrscheinlichkeitsverteilungen für einen Anteil der Vegetarier von $p_0=0,3$ und $p_1=0,4$ dargestellt. Begründe die Lage des Maximums der zu $p_1=0,4$ gehörigen Verteilung.
Zeichne die Fläche ein, deren Inhalt ein Maß für die Wahrscheinlichkeit eines Fehlers 2. Art darstellt, wobei die Annahme aus Aufgabe 3.3 weiterhin zugrunde gelegt wird.

he mathe abi lk cas 2022 binomialverteilung

Material 2
Binomialverteilung $B_{150;p}(k)$ für $p_0=0,3$ und $p_1=0,4$

(4 BE)

3.5

Erläutere anhand des Diagramms in Material 2, wie sich die Wahrscheinlichkeit für einen Fehler 2. Art entwickelt, wenn der tatsächliche Anteil $p$ der Vegetarier von $40 \;\%$ kontinuierlich bis auf $100 \%$ steigt.
Begründe, dass für $p \leq 0,3$ die Wahrscheinlichkeit, $H_0$ beizubehalten, mindestens $95,29 \;\%$ ist, wenn beim Hypothesentest aus Aufgabe 3.1 die Wahrscheinlichkeit für einen Fehler 1. Art höchstens $4,71 \;\%$ beträgt.

Begründe, warum man für $p \leq 0,3$ den Fehler 2. Art nicht begehen kann.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Anzahl $N_1$ berechnen

Rechenweg anzeigen

$N_1=3\cdot 4\cdot 4=48$

Anzahl $N_2$ berechnen

Laut Aufgabenstellung spielt die Reihenfolge der Speisen keine Rolle. Dadurch ergibt sich:

Rechenweg anzeigen

$N_2=\pmatrix{3\\2}\cdot 4= 3\cdot 4 = 12$

Anzahl $N_3$ berechnen

1. Fall: Vorspeise, Hauptspeise, Dessert:

Rechenweg anzeigen

$N_{3a}=2\cdot 2\cdot 4=16$

2. Fall: Vorspeise 1, Vorspeise 2, Hauptspeise:

Da es nur zwei vegetarische Vorspeisen gibt, ist hier bereits festgelegt, welche Vorspeisen gewählt werden.

Rechenweg anzeigen

$N_{3b}=1\cdot 2=2$

$N_3=N_{3a}+N_{3b}=16+2=18$

2.1

Bei der Bestimmung von Wahrscheinlichkeiten kann man genau dann von Bernoulliketten ausgehen, wenn ein Experiment mit nur zwei möglichen Ergebnissen n-mal unabhängig voneinander wiederholt werden kann.

2.2

Ereignis A

$P(A)=\binom{10}{4}\cdot 0,3^4\cdot 0,7^6 \approx 0,201=20,01\,\%$

Ereignis B

$X$ beschreibt die Anzahl der Besucher der Kantine, welche die Spaghetti wählen.

$X$ ist binomialverteilt mit $n=50$ und $p=0,2$ .

$P(X\leq 8)\approx0,3073=30,73\,\%$

Ereignis C

$X$ beschreibt die Anzahl der Besucher der Kantine, welche das Schnitzel wählen.

$X$ ist binomialverteilt mit $n=100$ und $p=0,35$ .

$\begin{array}[t]{rll} P(C)&=&P(X\leq 40)-P(X\leq 29) &\\[5pt] &\approx & 0,7514 \\[5pt] &= & 75,14 \,\% \\[5pt] \end{array}$

Ereignis D

$X$ beschreibt die Anzahl der Besucher der Kantine, welche die Lachsröllchen wählen.

$Y$ beschreibt die Anzahl der Besucher der Kantine, welche den kleinen Salat wählen.

$X$ ist binomialverteilt mit $n=4$ und $p=\dfrac{1}{3}$ .

$Y$ ist binomialverteilt mit $n=16$ und $p=\dfrac{1}{3}$ .

$\begin{array}[t]{rll} P(D)&=&P(X=4)\cdot P(Y=5) & \\[5pt] &\approx&0,0026 & \\[5pt] &=&0,26\,\% \end{array}$

2.3.1

Ereignis E

$P(K)$ beschreibt die Wahrscheinlichkeit, dass ein vegetarischer Besucher die Käsespätzle wählt. Diese beträgt $50\,\% .$

$P(E)=15\,\%$

Rechenweg anzeigen

Ereignis F

Es handelt sich um eine bedingte Wahrscheinlichkeit, die mit dem Satz von Bayes bestimmt wird. Es gilt:

$P_K(V)= \dfrac{P_V(K)\cdot P(V)}{P(K)}$

$P(K)$ beschreibt die Wahrscheinlichkeit, dass ein zufälliger Besucher die Käsespätzle wählt und beträgt $25\,\% .$

Der Anteil der Vegetarier unter den Besuchern, die die Käsespätzle wählen, beträgt

$\dfrac{0,5\cdot 0,3}{0,25}=\dfrac{0,15}{0,25}=0,6=60\,\%.$

Ereignis G

Es gilt:

$\begin{array}[t]{rll} P(K)&=& 0,25 \\[5pt] P(V) \cdot P_V(K) +P(\overline{V})\cdot P_{\overline{V}}(K)&=&0,25 \\[5pt] 0,3 \cdot 0,5 +0,7 \cdot P_{\overline{V}}(K) &=& 0,25 \end{array}$

Hier gilt außerdem $P_{\overline{V}}(K) =P(G)$ und somit folgt:

$\begin{array}[t]{rll} 0,15 +0,7 \cdot P(G)&=& 0,25 &\quad \scriptsize \mid\; -0,15\\[5pt] 0,7 \cdot P(G)&=& 0,1&\quad \scriptsize \mid\; :0,7\\[5pt] P(G)&=& \dfrac{1}{7} \\[5pt] &\approx& 0,143 \end{array}$

Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Besucher, der kein Vegetarier ist, sich für Käsespätzle entscheidet, beträgt $14,3 \;\%.$

2.3.2

Bedingung für stochastische Unabhängigkeit:

$P(V\cap K)=P(V)\cdot P(K)$

$P(V\cap K)$ entspricht dem Anteil der Besucher, welche vegetarisch sind und die Käsespätzle wählen. Da die beiden vegetarischen Hauptspeisen bei den Vegetariern gleich beliebt sind, folgt:

$P(V\cap K)=30\,\% \cdot 0,5= 15 \,\%$

Aus $P(V)=0,3$ und $P(K)=0,25$ ergibt sich jedoch:

$P(V)\cdot P(K)=0,3\cdot 0,25=0,075= 7,5 \,\%$

Da die Bedingung für stochastische Unabhängigkeit somit nicht erfüllt ist, sind die beiden Merkmale $V$ und $K$ stochastisch abhängig voneinander.

3.1

Rechtsseitiger Hypothesentest

$p$ beschreibt hierbei den prozentualen Anteil der Besucher der Kantine, weche Vegetarier sind.

$H_0:$ Der Anteil der Vegetarier beträgt $30\,\%: p\leq 0,3$

$H_1:$ Der Anteil der Vegetarier beträgt mehr als $30\,\%: p\gt 0,3$

Ablehnungsbereich bestimmen

$X$ beschreibt die Anzahl der vegetarischen Besucher der Kantine.

$X$ ist binomialverteilt mit $n=150$ und $p=0,3.$

Mit dem WTR ergibt sich:

$P(X\geq 54)=1-P(X\lt 54)\approx 1-0,933$

$\begin{array}[t]{rll} P(X\geq 55)&=& 1-P(X\lt 55) & \\[5pt] &\approx& 1-0.953 & \\[5pt] &\lt& 0,05 \end{array}$

Somit folgt der Ablehnungsbereich mit $\overline{A}=[55;150]$

Entscheidungsregel

Geben mindestens 55 der 150 befragten Besucher an, Vegetarier zu sein, so wird die Nullhypothese abgelehnt und angenommen, dass mehr als $30\,\%$ der Besucher vegetarisch sind.

Entscheidung

Da 57 Personen bei der Befragung angeben, Vegetarier zu sein, ist also davon auszugehen, dass der Anteil der Vegetarier gestiegen ist.

3.2

Fehler 1. Art

Der Fehler 1. Art ist eine irrtümliche Ablehnung der Nullhypothese.

Es wird also davon ausgegangen, dass der Anteil der Vegetarier gestiegen ist, obwohl dies in Wirklichkeit nicht der Fall ist.

Mögliche Konsequenzen wären die erhöhte Zubereitung der vegetarischen Speisen sowie eine größere Auswahl an vegetarischen Mahlzeiten.

Fehler 2. Art

Der Fehler 2. Art ist eine irrtümliche Annahme der Nullhypothese.

Beim Fehler 2. Art wird davon ausgegangen, dass sich der Anteil der vegetarischen Besucher nicht erhöht hat, obwohl dieser in Wirklichkeit gestiegen ist.

Mögliche Konsequenzen sind, dass zu wenige vegetarische Speisen produziert und angeboten werden.

3.3

$X$ beschreibt die Anzahl der vegetarischen Besucher der Kantine.

$X$ ist binomialverteilt mit $n=150$ und $p=0,4.$

$P(X\leq 54)\approx 0,18=18\,\%$

Die Wahrscheinlichkeit für den Fehler 2. Art bei einer tatsächlichen Erhöhung des Anteils der Vegetarier auf $45\,\%$ beträgt somit ungefähr $18\,\%.$

3.4

Da für $p_1=0,4$ der Anteil der Vegetarier höher ist als bei $p_0=0,3$ , liegt das Maximum weiter in positiver Richtung auf der $x$ -Achse.

Der Erwartungswert lässt sich berechnen durch $\mu=150\cdot 0,4=60.$

Einzeichnen der Fläche, die ein Maß für die Wahrscheinlichkeit eines Fehlers 2. Art darstellt:

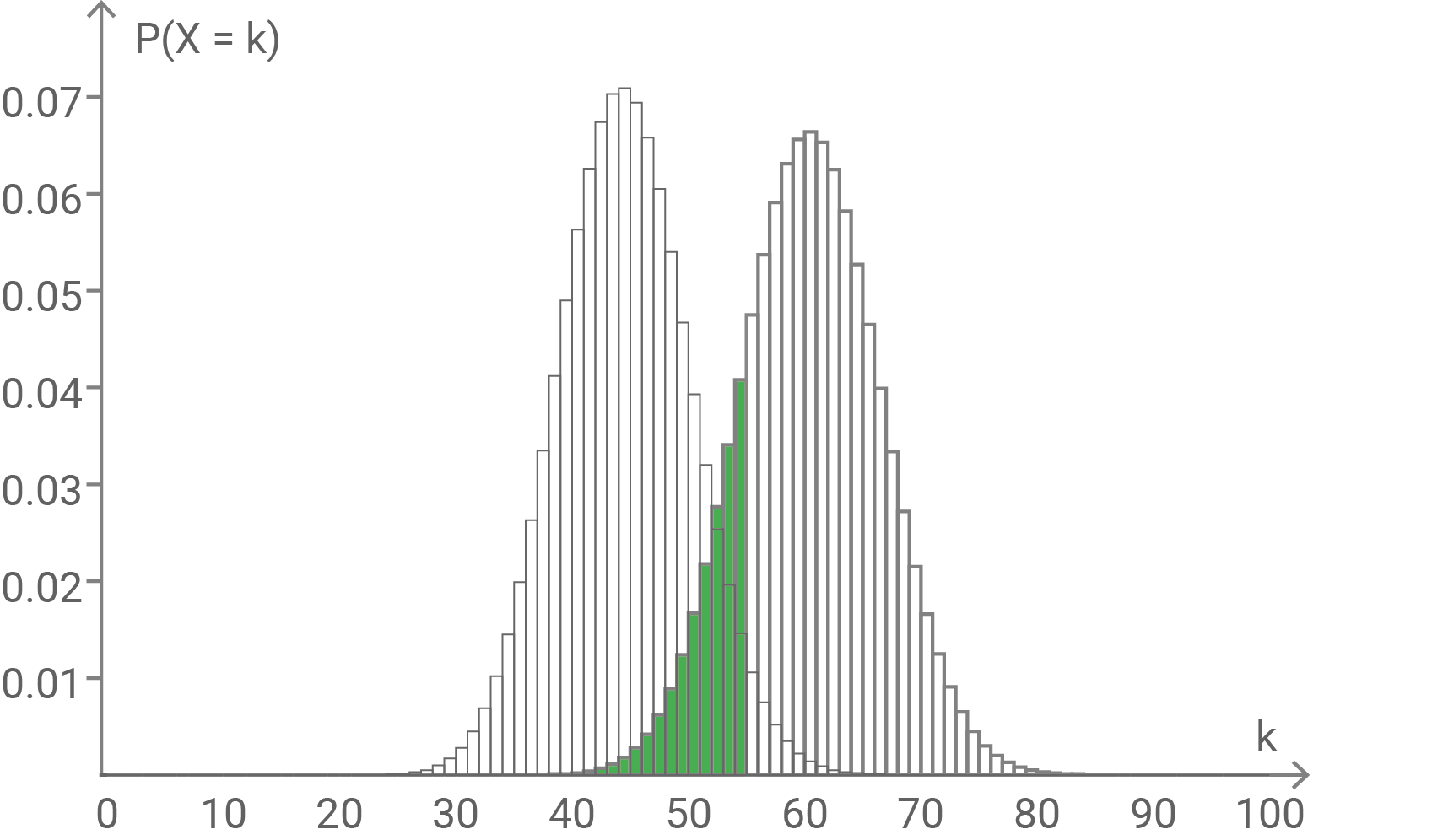
Hessen Abi Stochastik Binomialverteilung Fehler zweiter Art

3.5

Erläuterung des Diagramms

Je höher der Anteil $p$ der Vegetarier, desto größer wird der Erwartungswert. Mit steigendem Anteil wandert die Verteilung somit auf der $x$ -Achse immer weiter in positive Richtung und entfernt sich zunehmend vom Annahmebereich der Verteilung mit $p_0=0,3.$

Die Wahrscheinlichkeit, dass die alternative Hypothese fälschlicherweise angenommen wird, nimmt folglich mit steigendem Anteil $p$ kontinuierlich ab.

Begründung Fehler 1. Art

Der Fehler 1. Art entspricht dem Signifikanzniveau $\alpha$ .

Beträgt dieses nur noch höchstens $4,71\,\%$ , so wird der Annahmebereich der Nullhypothese größer. Der Grenzwert des Annahmebereichs wird so berechnet, dass die Gesamtwahrscheinlichkeit des Bereichs $100\,\%-\alpha$ beträgt. Für ein Signifikanzniveau von höchstens $4,71\,\%$ ergibt sich somit eine Wahrscheinlichkeit von mindestens $95,29\,\%$ , dass $H_0$ beibehalten wird.

Begründung Fehler 2. Art

Der Fehler 2. Art entspricht der irrtümlichen Annahme der Nullhypothese.

Da die Nullhypothese jedoch ebenfalls als $p\leq0,3$ gewählt wurde, ist diese für $p\leq0,3$ immer korrekt. Es kann also zu keiner irrtümlichen Annahme kommen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?