A1 - Analysis

Die Bestimmung von Enzymaktivitäten in Serum, Plasma oder Harn hat in der medizinischen Diagnostik eine wichtige Bedeutung. Beispielsweise ist bei einem Herzinfarktpatienten die Serum-Enzymaktivität bestimmter Enzyme auch Tage nach dem Infarkt noch erhöht, sodass eine Spätdiagnose über die Messung der Enzymaktivität möglich ist.

Der Verlauf einer bestimmten Enzymaktivitätskurve lässt sich durch den Graphen einer Exponentialfunktion der Schar $f_{a, b, c}$ mit $f_{a, b, c}(t)=a+b\cdot t^2\cdot \mathrm{e}^{c\cdot t}$ $(a, b > 0$ und $c \lt 0 )$ approximieren:

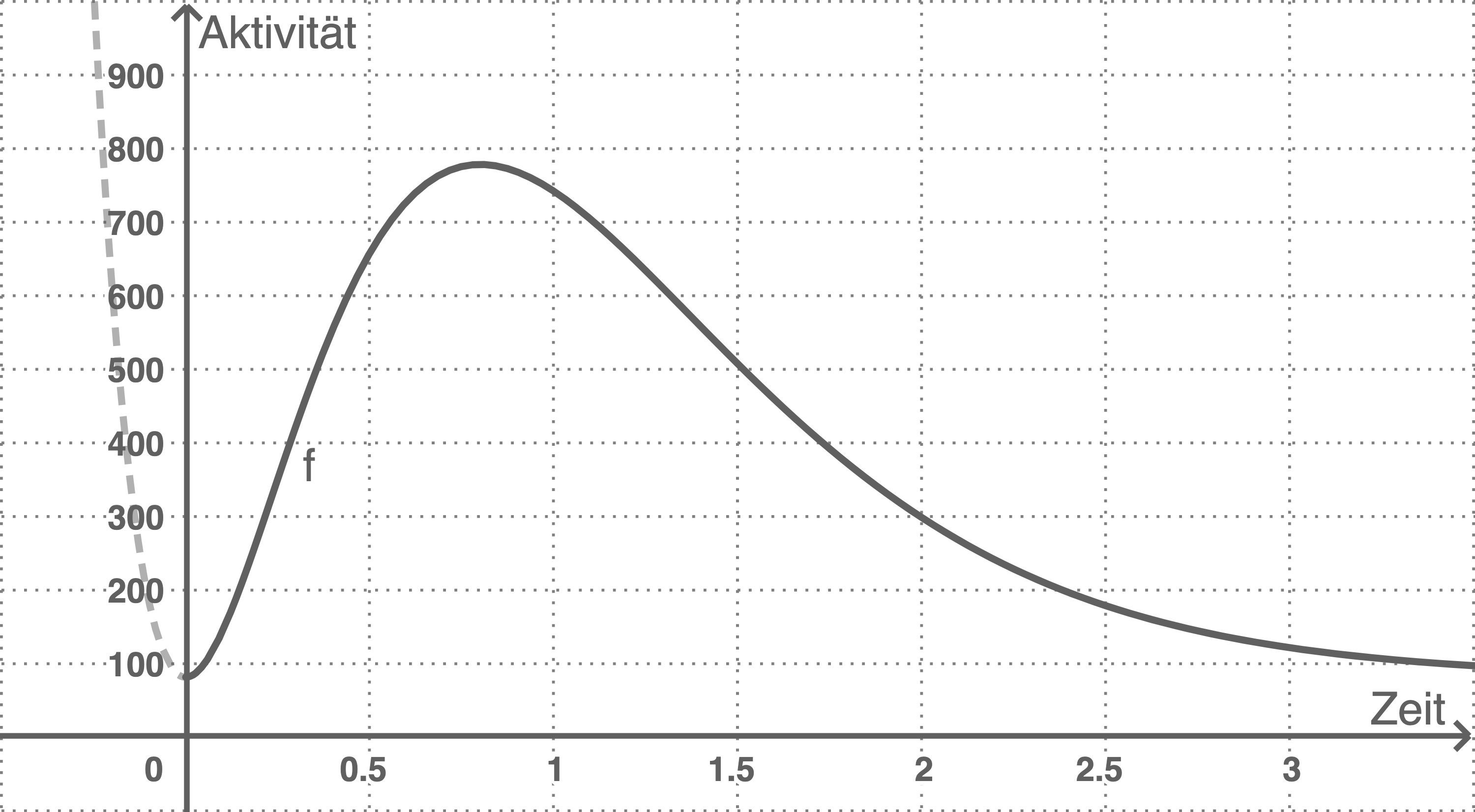Enzymaktivitaet Funktionenschar Hessen Abi 2015

Dabei steht $t$ für die Zeit in Tagen seit Beginn einer Erkrankung und $f(t)$ für die Enzymaktivität in Units (Substraktumsatz pro Tag).

Bestimme die Parameter $a$ , $b$ und $c$ unter Berücksichtigung der folgenden Angaben:

Die Enzymaktivität beträgt zu Beginn 80 Units.

Bereits nach einem Tag ist die Enzymaktivität auf den Wert 740 Units gestiegen.

Drei Tage nach Beginn hat sich die Enzymaktivität wieder weitgehend normalisiert und beträgt nur noch 120 Units.

(9 BE)

Um einen Herzinfarkt zu diagnostizieren, misst man beispielsweise die Aktivität des Enzyms Creatin-Kinase. Bei einem bestimmten Patienten kann die Aktivitätskurve für dieses Enzym für $0 \leq t \leq 5$ durch den Graphen der Exponentialfunktion $f$ mit $f(t)=100+4600\cdot t^2 \cdot \mathrm{e}^{-2\cdot t}$ angenähert werden, wobei $t$ für die Zeit in Tagen nach dem Infarkt steht und $f(t)$ für die Enzymaktivität in Units. Ca. 3 Tage nach einem Herzinfarkt befindet sich die Aktivität dieses Enzyms wieder im Normalbereich.

2.1

Zeige rechnerisch, dass gilt: $\(f$

(6 BE)

2.2

Berechne die Zeitpunkte, zu denen die Aktivitätskurve für das Enzym Creatin-Kinase am stärksten ansteigt bzw. am stärksten fällt, sowie jeweils die zugehörigen Änderungsraten.

Hinweis: Die Überprüfung der notwendigen Bedingung ist ausreichend.

(6 BE)

2.3

Die Ermittlung einer Stammfunktion von $f$ kann durch eine bestimmte Integrationsmethode angedeutet werden:

Material anzeigen

2.3.1

Gib die Integrationsmethode an und leite durch Vervollständigung der Rechnung eine Stammfunktion $F$ von $f$ her.

(6 BE)

2.3.2

Bestimme das Integral $\dfrac{1}{3}\cdot \displaystyle\int_{0}^{3} f(t) dt$ und deute das Ergebnis im Sachzusammenhang.

(4 BE)

2.4

Die Entscheidung für die Diagnose Herzinfarkt liege bei einer Enzymaktivität des Enzyms Creatin-Kinase von mindestens 192 Units. Zeige, dass der Ansatz $100+4600\cdot t^2 \cdot \mathrm e^{-2\cdot t}=192$ zu der Gleichung $\ln\left(t^2\right)=2\cdot t - 3,91202$ führt. Diese Gleichung lässt sich nicht algebraisch lösen.

Erläutere die folgende Darstellung und untersuche mithilfe der Graphen näherungsweise, in welcher Zeitspanne die Diagnose Herzinfarkt gestellt werden kann.

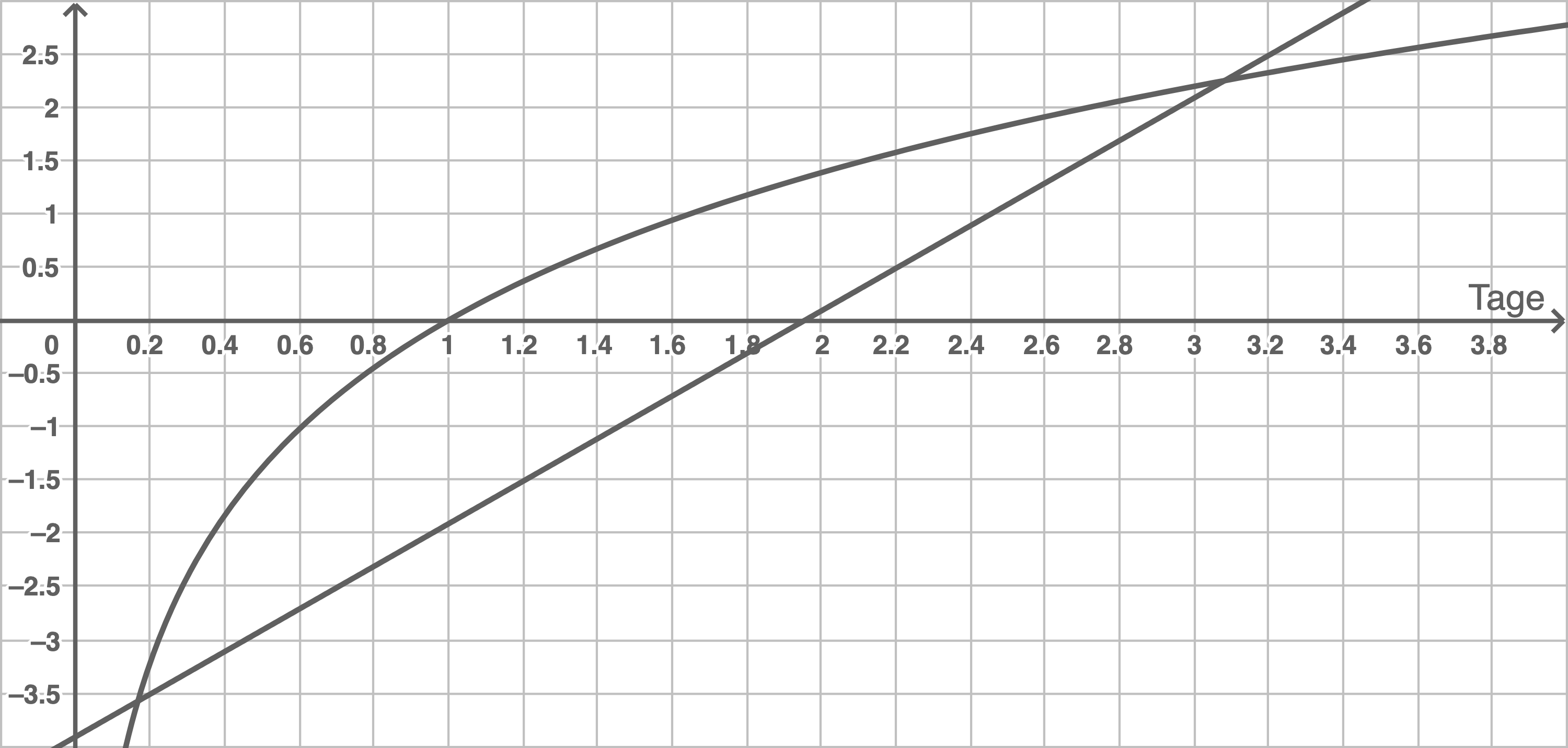
(10 BE)

1. Schritt: Vorgegebene Bedingungen einsetzen

Aus der ersten Angabe folgt:

$\begin{array}[t]{rll} f_{a,b,c}(0)&=& 80 & \\[5pt] a+b \cdot 0^2\cdot \mathrm{e}^{c\cdot 0}&=& 80 &\\[5pt] a&=& 80 \end{array}$

Aus der zweiten Angabe folgt:

$\begin{array}[t]{rll} f_{a,b,c}(1)&=& 740 & \\[5pt] a+b \cdot 1^2\cdot \mathrm{e}^{c\cdot 1}&=& 740 &\quad \scriptsize \mid\; a=80\\[5pt] 80+b \cdot \mathrm{e}^{c}&=& 740 &\\[5pt] \end{array}$

Aus der dritten Angabe folgt:

$\begin{array}[t]{rll} f_{a,b,c}(3)&=& 120 & \\[5pt] a+b \cdot 3^2\cdot \mathrm{e}^{c\cdot 3}&=& 120 &\quad \scriptsize \mid\; a=80\\[5pt] 80+9b \cdot \mathrm{e}^{3c}&=& 120 &\\[5pt] \end{array}$

2. Schritt: Gleichungssystem aufstellen

Mit dem Einsetzungsverfahren ergibt sich:

Gleichungssystem anzeigen

Somit sind die gesuchten Parameter $a=80$ , $b=8.042,8$ und $c=-2,5$ .

Die Funktionsgleichung lautet folglich:

$f_{80;\,8042,8;\,-2,5}(t)=80+8.042,8 \cdot t^2\cdot e^{-2,5 \cdot t}.$

2.1

Mit der Produkt- und Kettenregel können die ersten beiden Ableitungen von $f(t)=100+4600\cdot t^2\cdot \mathrm e^{-2\cdot t}$ bestimmt werden:

$\(\begin{array}{rll} f$

$\( f$

Rechenweg anzeigen

2.2

Die Zeitpunkte des stärksten Anstiegs beziehungsweise der stärksten Abnahme beschreiben die Wendestellen der Funktion $f$ und somit den Extrempunkten der ersten Ableitung $\(f$

1. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} f$

Da $9200 \gt 0$ und $\mathrm{e}^{-2t}\gt 0$ gilt, folgt mit dem Satz vom Nullprodukt:

$\begin{array}[t]{rll} 2t^2-4t+1&=& 0 &\quad \scriptsize \mid\; :2\\[5pt] t^2-2t+\dfrac{1}{2}&=& 0 \end{array}$

Mit der $pq$ -Formel ergibt sich für $p=-2$ und $q=\dfrac{1}{2}:$

$\begin{array}{rll} t_{1,2} =& - \dfrac{(-2)}{2} \pm \sqrt{\left( {\dfrac{-2}{2}} \right)^2 - \dfrac{1}{2}} \\[5pt] t_{1,2} =& 1 \pm \sqrt {1 - \dfrac{1}{2}}\\[5pt] t_{1,2} =&1 \pm \dfrac{1}{\sqrt {2}} \end{array}$

Da laut Aufgabenstellug nur die notwendige Bedingung geprüft werden muss, folgen die Wendestelle von $f$ also mit $t_1=1 + \dfrac{1}{\sqrt {2}}$ und $t_2=1 - \dfrac{1}{\sqrt {2}}.$

2. Schritt: Änderungsraten bestimmen

$\( t_1: \; \; f$

Rechenweg anzeigen

$\( t_2: \; \; f$

Rechenweg anzeigen

3. Schritt: Randwerte überprüfen

$\(\begin{array}[t]{rll} t=0: \; \; f$

$\(\begin{array}[t]{rll} t=5: \; \; f$

Damit befinden sich am Rand keine Wendestellen.

Die Aktivitätskurve fällt zum Zeitpunkt $t_1$ mit einer Änderungsrate von $-365,39$ und folglich am stärksten. Zum Zeitpunkt $t_2$ steigt die Aktivitätskurve mit einer Änderungsrate von $1.060,67$ am stärksten.

2.3

2.3.1

Integrationsmethode angeben

Die Integralgleichung im Material 2 ist von der Form

Gleichung anzeigen

mit $u(t)=4600 \cdot t^2$ und $v(t)=\left( -\dfrac{1}{2}\right) \cdot \mathrm{e}^{-2t}.$

Bei der Integration in Material 2 handelt es sich folglich um die Methode der partiellen Integration.

Stammfunktion herleiten

1. Schritt: Integral berechnen

$\displaystyle\int_{}^{}4600 \cdot t \cdot \mathrm{e}^{-2 \cdot t} \mathrm dt = ...$

Rechenweg anzeigen

2. Schritt: Ergebnis einsetzen

Rechenweg anzeigen

$\displaystyle\int_{}^{}f(t)\;\mathrm dt=...$

Für $c=0$ folgt also eine Stammfunktion $F$ von $f$ mit:

$F(t)=100t - 1.150 \cdot \mathrm{e}^{-2t} \cdot \left(2t^2+2t+1\right)$

2.3.2

Integral bestimmen

Rechenweg anzeigen

$\dfrac{1}{3} \displaystyle\int_{0}^{3} f(t) \mathrm dt \approx 459,58$

Ergebnis deuten

Nach Aufgabenstellung beschreibt die Funktion $f$ die Enzymaktivität in Units. Dabei steht $t$ für die Tage, die seit dem Infarkt vergangen sind. Das Integral $\displaystyle\int_{0}^{3} f(t) \mathrm dt$ beschreibt damit die gesamte Menge an Enzymaktivität in Units, die 3 Tage nach dem Infarkt insgesamt ausgeschüttet wurde.

Teilt man dies durch 3, so erhält man die durschnittliche Enzymaktivität der ersten 3 Tage in Units pro Tag.

Also lag die durchschnittliche Enzymaktivität während der ersten drei Tage nach dem Infarkt bei 459,58 Units pro Tag.

2.4

Gleichung zeigen

Rechnung anzeigen

Darstellung erläutern

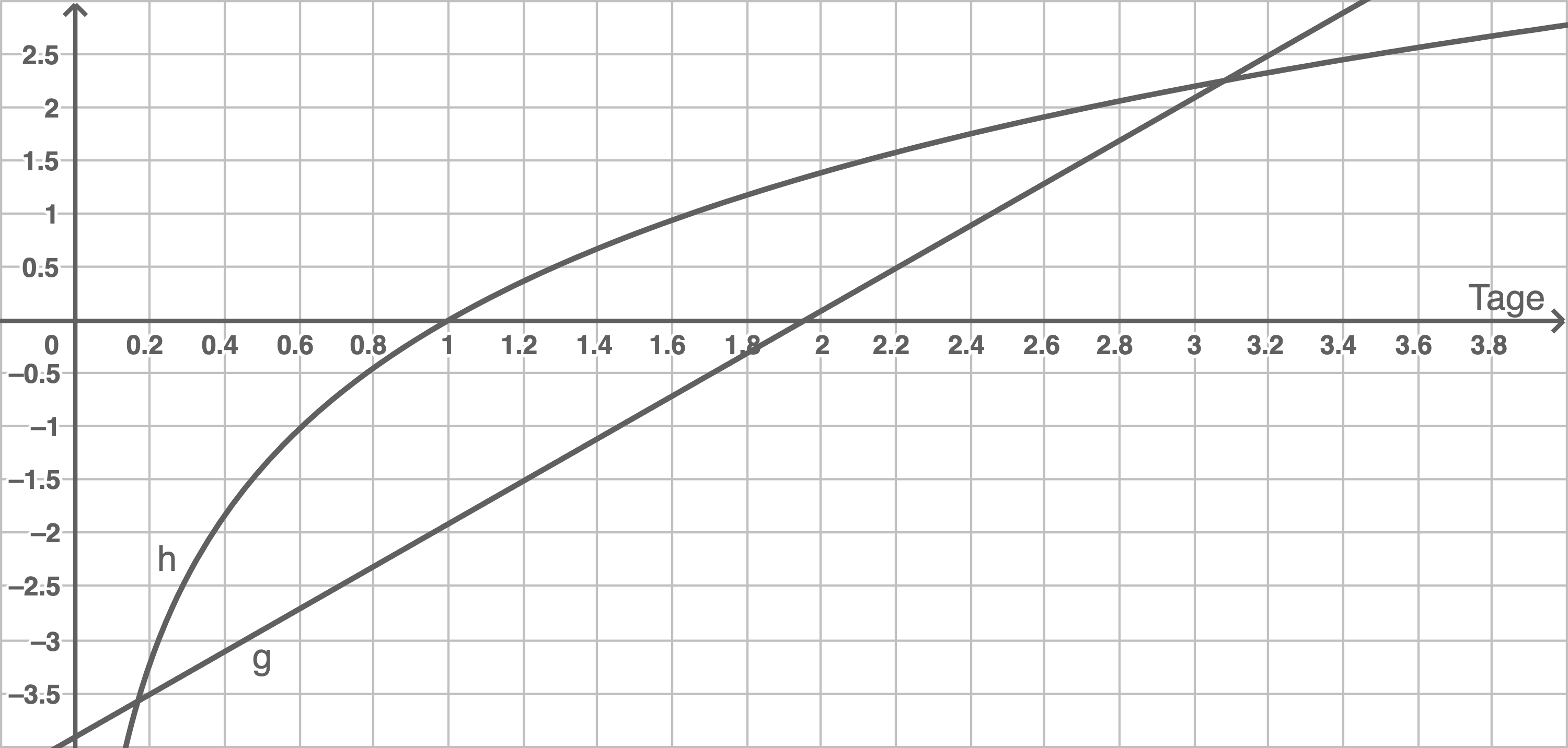
Die Darstellung zeigt eine Kurve und eine Gerade, wobei die Gerade die $y$ -Achse bei etwa -3,9 schneidet und eine Steigung von 2 hat. Die Gerade gehört folglich zum Term $g(t)=2t - 3,91202.$

Die Kurve hat eine Nullstelle bei $x=1$ , und der Graph nähert sich asymptotisch der $y$ -Achse an, besitzt also Eigenschaften der Logarithmusfunktion. Der Graph gehört folglich zur Gleichung $h(t)=\ln{(t^2)}$ , also zur linken Seite der obigen Gleichung.

Hilfsskizze Diagnose Herzinfarkt Hessen Abi 2015

Beschriftete Skizze

Zeitspanne untersuchen

Nach Aufgabenstellung wird ein Herzinfarkt diagnostiziert, wenn die Enzymaktivität mindestens 192 beträgt. Also wird zu jedem $t$ mit $0\leq t \leq 5,$ welches die Ungleichung $100+4.600 \cdot t^2 \cdot \mathrm{e}^{-2t}\geq 192$ erfüllt, die Diagnose Herzinfarkt gestellt.

Diese Ungleichung ist wie oben gezeigt äquivalent zu

$h(t)=\ln{(t^2)}\geq 2t - 3,91202=g(t)$

Aus der Abbildung lässt sich ablesen, dass dies im Intervall $\left[0,17; 3,08\right]$ gilt.

Die Enzymaktivität ist in diesem Intervall folglich auch größer oder gleich 192.

Die Diagnose eines Herzinfarkts kann also ab etwa 4 Stunden nach dem Infarkt bis etwa 3 Tage nach dem Infarkt gestellt werden.