A2 - Analysis

Ende April eines jeden Jahres fangen die ersten Larven an aus den Eiern zu schlüpfen. In dieser Zeit beginnt die Larvenphase, in der sich die Larven von den Nadeln der Lärchen ernähren, bis sie sich zu verpuppen beginnen. Der Lärchenwickler zählt zu den Forstschädlingen. Er ruft besonders schwere Schäden bei der in den Alpen verbreiteten Europäischen Lärche hervor.

1.1

Die Größe einer Larve in $\text{mm}$ lässt sich in den ersten Lebenstagen durch eine Exponentialfunktion $f$ der Form $f(t) = a \cdot \mathrm e^{k \cdot t}$ ( $t:$ Zeit in Tagen nach dem Schlüpfen) mit $a,k \gt 0$ modellieren. Berechne mithilfe der Daten für $t = 1$ und $t = 10$ der folgenden Tabelle die zugehörige Funktion $f.$
Die Modellierung kann als gut bezeichnet werden, wenn die Abweichung der Daten von den im Modell ermittelten Werten maximal $3 \,\%$ beträgt.
Prüfe anhand der übrigen Daten, ob die Modellierung als gut bezeichnet werden kann.

$\color{#fff}{t}$ (in Tagen)	Larvengröße (in $\color{#fff} {\,\text{mm}}$ )
$1$	$3,2$
$2$	$3,5$
$4$	$4,1$
$10$	$7,3$

(7 BE)

1.2

Alternativ lässt sich die Größe einer Larve in $\text{mm}$ mithilfe der Funktion $g$ mit $g(t)=\dfrac{19,4}{1 + 5,72 \cdot \mathrm e^{-0,12 \cdot t}}$ ( $t:$ Zeit in Tagen nach dem Schlüpfen) modellieren.
Für die Funktion $g$ gilt:

Funktion anzeigen

1.2.1

Begründe anhand des Funktionsterms, dass die sogenannte Sättigungsgrenze $S = \lim_{t\to\infty} g(t)$ der Funktion $g$ den Wert $19,4$ annimmt, und deute diesen Wert im Sachzusammenhang. Begründe, warum die Funktion $g$ die Größe einer Larve für große Werte von $t$ besser beschreibt als die Funktion $f.$

(4 BE)

1.2.2

Zeige unter Verwendung der Eigenschaft $(\text{I}),$ dass gilt:

Funktion anzeigen

(4 BE)

1.2.3

Zeige unter Verwendung des Terms von $\(g$ aus Aufgabe 1.2.2 und der Eigenschaft $(\text{II}),$ dass zu dem Zeitpunkt innerhalb des betrachteten Intervalls, an dem die Larve am stärksten wächst, die Hälfte der Sättigungsgrenze aus Aufgabe 1.2.1 erreicht wird.
Berechne diesen Zeitpunkt.
Hinweise: Die Untersuchung der notwendigen Bedingung ist ausreichend. Eine Randwertbetrachtung ist nicht erforderlich.

(7 BE)

In gewissen Regionen in den Alpen traten die Massenvermehrungen des Lärchenwicklers seit Beobachtungsbeginn im Jahr 1989 $(t = 0)$ mit erstaunlicher Regelmäßigkeit alle 9 Jahre auf. Die maximale Larvendichte (Anzahl der Larven pro $\,\text{kg}$ Zweige) eines jeden Kalenderjahres in Abhängigkeit von der Zeit $t$ in Jahren nach Beobachtungsbeginn kann mit der Funktion $k$ mit

Funktion anzeigen

näherungsweise modelliert werden. Jahreszeitlich bedingte Schwankungen werden bei dieser Modellierung nicht berücksichtigt. Der Graph von $k$ ist in Material 1 dargestellt.

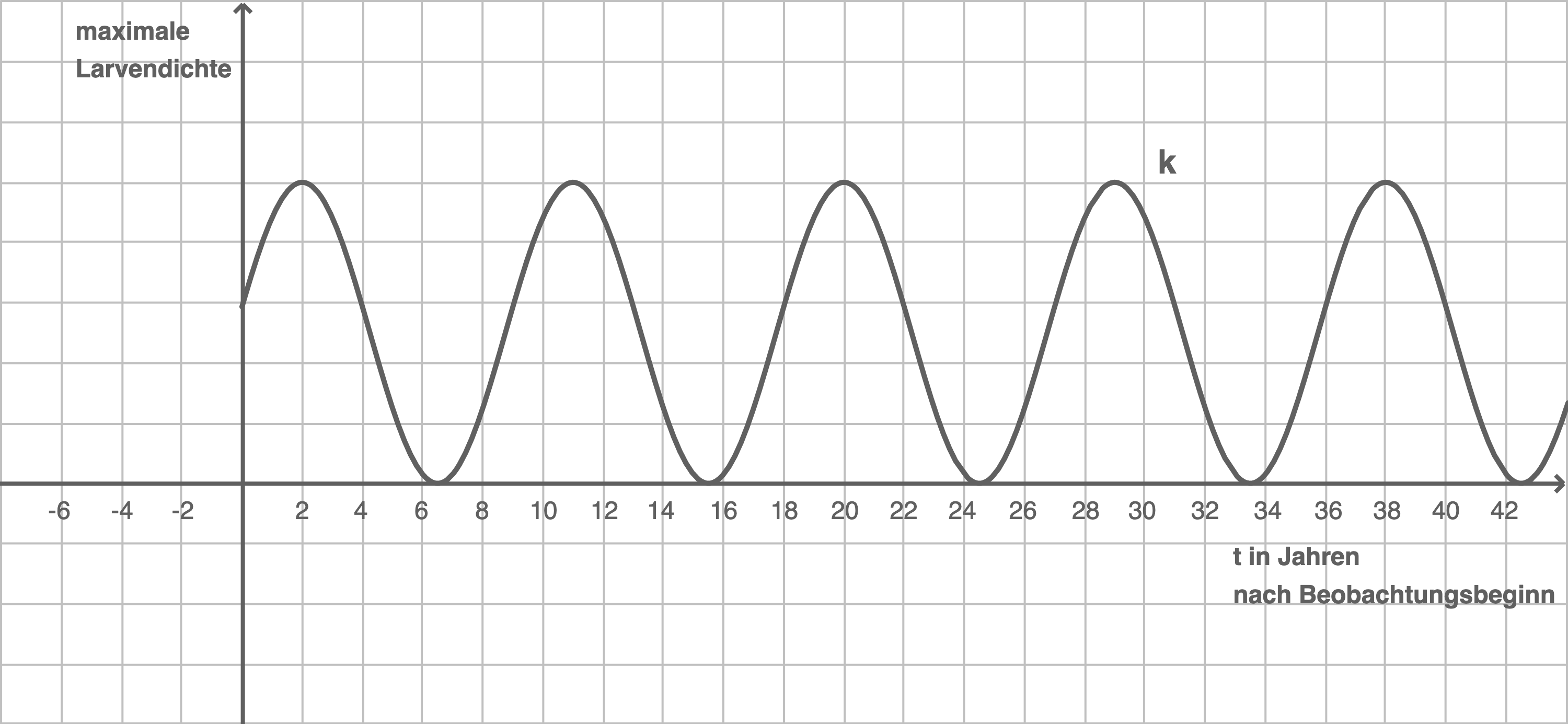
Material 1

2.1

Beschreibe, wie der Graph von $k$ aus dem Graphen der allgemeinen Sinusfunktion $s$ mit $s(t) = \sin(t)$ hervorgeht, und bestätige rechnerisch, dass $k$ die Periode $9$ hat.

(5 BE)

2.2

Ein Befall wird erst sichtbar, wenn der Wert der maximalen Larvendichte größer als $100$ ist.
Erläutere den Rechenansatz in der Zeile ( $\text{ I }$ ) des Kastens im Sachzusammenhang und zeige mithilfe des Ergebnisses in Zeile ( $\text{ III }$ ), dass der Befall ab dem Jahr 2022 erstmals nach 2018 wieder nicht mehr sichtbar ist.

Funktionsgleichung anzeigen

(7 BE)

2.3

Um die zu erwartende durchschnittliche maximale Larvendichte pro Jahr im Zeitraum von 2018 bis einschließlich 2037 zu berechnen, werden zwei Strategien verfolgt:

$(\text{I})$

Bestimmung von $d_{\text{I}}$ wie in Material 2 angegeben.

$(\text{II})$

Bestimmung von $d_{\text{II}}$ unter Verwendung der Funktion $k$ und dem Ansatz $d_{\text{II}} = \frac{1}{20}\displaystyle\int_{28,5}^{48,5}k(t)\;\mathrm dt.$

Erläutere die beiden Strategien.
Bestimme $d_{\text{II}}$ unter Verwendung der Funktion $k$ und dem Ansatz und vergleiche diesen Wert mit $d_{\text{I}}.$

Material 2

$\color{#fff}{t}$	$\color{#fff}{k(t)}$
$29$	$500$
$30$	$441,52$
$31$	$293,43$
$...$	$...$
$46$	$441,52$
$47$	$500$
$48$	$441,52$

$d_1$ anzeigen

(6 BE)

1.1

Funktion berechnen

Mit den beiden Werten aus der Tabelle für $t=1$ und $t=10$ ergeben sich folgende Gleichungen:

$\begin{array}{lrll} \text{I}\quad&3,2&=& f(1) \\ &3,2&=& a\cdot \mathrm e^{k\cdot 1} \\ &3,2&=& a\cdot \mathrm e^{k} \\[5pt] \text{II}\quad&7,3&=& f(10) \\ &7,3&=& a\cdot \mathrm e^{k\cdot 10} \\ \end{array}$

Durch Auflösen der ersten Gleichung nach $a$ ergibt sich:

$\begin{array}[t]{rll} 3,2 &=& a\cdot \mathrm e^{k} &\quad \scriptsize \mid\;:\mathrm e^{k} \\[5pt] \dfrac{3,2}{\mathrm e^k} &=& a \end{array}$

Einsetzen in die zweite Gleichung liefert:

$\begin{array}[t]{rll} 7,3&=& \dfrac{3,2}{\mathrm e^k} \cdot \mathrm e^{k\cdot 10} \\[5pt] 7,3&=& \dfrac{3,2}{\mathrm e^k} \cdot \left(\mathrm e^{k}\right)^{10} \\[5pt] 7,3&=& 3,2\cdot \left(\mathrm e^{k}\right)^{9} \\[5pt] 7,3&=& 3,2\cdot \mathrm e^{9k} &\quad \scriptsize \mid\;:3,2 \\[5pt] \dfrac{7,3}{3,2}&=& \mathrm e^{9k} &\quad \scriptsize \mid\; \ln \\[5pt] \ln \left(\dfrac{7,3}{3,2} \right) &=& 9k &\quad \scriptsize \mid\; :9\\[5pt] 0,092&\approx& k \\[5pt] \end{array}$

Durch Einsetzen in $a$ folgt:

$a= \dfrac{3,2}{\mathrm e^{0,092}} \approx 2,919$

Eine Gleichung der Funktion $f$ lautet also $f(t)= 2,919 \cdot \mathrm e^{0,092\cdot t}.$

Modellierung prüfen

Abweichung zwischen den Modellwerten und den Daten berechnen:

$\begin{array}[t]{rll} \dfrac{3,5 - f(2)}{3,5} &=& \dfrac{3,5 - 2,919 \cdot \mathrm e^{0,092\cdot 2} }{3,5} \\[5pt] &\approx& -0,002 \\[5pt] &=& -0,2\,\% \\[10pt] \dfrac{4,1 - f(4)}{4,1} &=& \dfrac{4,1 - 2,919 \cdot \mathrm e^{0,092\cdot 4} }{4,1} \\[5pt] &\approx& -0,029 \\[5pt] &=& -2,9\,\% \\[10pt] \end{array}$

Die größte Abweichung der Daten von den im Modell ermittelten Werten beträgt ca. $2,9\,\%$ und ist damit geringer als $3\,\%.$ Die Modellierung mit der Funktion $f$ kann daher als gut bezeichnet werden.

1.2.1

Sättigungsgrenze begründen

Für $t\to \infty$ gilt für den Nenner des Funktionsterms von $g:$

$\underbrace{1+5,72\cdot \underbrace{\mathrm e^{-0,12\cdot t}}_{\to 0}}_{\to 1}$

Für den gesamten Funktionsterm gilt daher $g(t) \to 19,4$ für $t\to \infty.$ Die Sättigungsgrenze der Funktion $g$ ist also $19,4$ und somit ist die Größe der Larven also auf $19,4\,\text{mm}$ begrenzt.

Mit der Zeit nähert sich die Größe zwar immer weiter dem Wert an, wird ihn aber niemals erreichen oder überschreiten. Die Larven können nach diesem Modell also nicht größer als $19,4\,\text{mm}$ werden.

Eignung der Funktionen begründen

Bei der Funktion $f$ handelt es sich um eine reine Exponentialfunktion. Es gilt $f(t)\to \infty$ für $t\to \infty.$ Die Larven würden bei diesem Modell also unendlich weiter wachsen ohne Begrenzung. Beim Modell mit der Funktion $g$ ist das Wachstum der Larve begrenzt. Dieses ist daher für große Werte von $t$ besser geeignet als die Funktion $f.$

1.2.2

Mit der Produktregel und der Eigenschaft $\text{I}$ folgt:

Rechenweg anzeigen

$\( g$

1.2.3

Zeitpunkt bestimmen

Die Wachstumsrate der Larve wird durch die Funktion $g‘$ beschrieben.

Der Zeitpunkt, zu dem die Larve am stärksten wächst, wird also durch die Stelle $t$ beschrieben, in der $\(g$ ihr Maximum annimmt. Dies entspricht der Wendestelle von $g.$

Notwendiges Kriterium für Wendestellen anwenden:

Rechenweg anzeigen

$g(t)=9,7$

Durch Einsetzen von $g(t)$ folgt:

Rechenweg anzeigen

$t \approx 14,53$

Da laut Aufgabenstellung weder die Überprüfung des hinreichenden Kriteriums noch eine Randwertbetrachtung erforderlich ist, wächst die Larve ca. $14,53$ Tage nach dem Schlüpfen am schnellsten.

Sättigungsgrenze nachweisen

Zu dem Zeitpunkt, an dem die Larve am schnellsten wächst, hat sie also eine Größe von ca. $9,70\,\text{mm}$ und damit die Hälfte der Sättigungsgrenze erreicht.

2.1

Graph $k$ beschreiben

Der Faktor $249,975$ vor dem Sinus-Term streckt den Graphen im Vergleich zur allgemeinen Sinusfunktion entlang der $y$ -Achse.

Durch den Faktor $b=\frac{2}{9}\pi$ innerhalb des Arguments wird die Periode $p$ verändert. Der Zusammenhang ist wie folgt:

$\begin{array}[t]{rll} b&=& \frac{2\pi}{p}&\quad \scriptsize \mid\; b= \frac{2}{9}\pi \\[5pt] \frac{2}{9}\pi&=& \frac{2\pi}{p} &\quad \scriptsize \mid\;\cdot p \\[5pt] \frac{2}{9}\pi\cdot p&=& 2\pi &\quad \scriptsize \mid\; :\left(\frac{2}{9}\pi \right) \\[5pt] p &=& 9 \end{array}$

Die Periode $p$ von $k$ wird also im Vergleich zu der Periode $2\pi$ von $s$ vergrößert, der Graph wird also entlang der $t$ -Achse gestreckt.

Durch den Summanden $+0,25$ wird der Graph von $k$ im Vergleich zu dem von $s$ um $0,25$ Einheiten nach links verschoben.

Durch den Summanden $250,025$ wird der Graph im Vergleich zur allgemeinen Sinusfunktion entlang der $y$ -Achse um $250,025$ Einheiten nach oben verschoben.

2.2

Rechenansatz erläutern

Die Funktion $k$ beschreibt die maximale Larvendichte eines jeden Kalenderjahres in Abhängigkeit von der Zeit $t$ in Jahren nach Beobachtungsbeginn. Ab einer Larvendichte von mehr als 100 Larven pro Kilogramm Zweige wird der Befall sichtbar.

In Zeile $\text{I}$ wird der Funktionsterm für die maximale Larvendichte mit $100$ gleichgesetzt. Der Ansatz dient also der Bestimmung der Zeitpunkte, zu denen der Befall sichtbar beziehungsweise nicht mehr sichtbar wird.

Ergebnis aus $\text{III}$ deuten

Die Ergebnisse aus Schritt $\text{III}$ stellen die Zeitpunkte dar, zu denen der Befall sichtbar bzw. nicht mehr sichtbar wird. Das Jahr 2018 entspricht dem Wert $t= 29,$ das Jahr 2022 entspricht dem Wert $t=33.$

Für die Werte $n=2$ und $n=3$ folgt:

Ergebnisse anzeigen

Folglich ist $t_2 \approx 32,172$ der erste Zeitpunkt nach dem Jahr 2018, also nach $t=29$ , zu dem die Larvendichte die Grenze $100$ passiert.
Der Abbildung in Material 1 kann entnommen werden, dass der Graph von $k$ an dieser Stelle fällt, die Larvendichte zu diesem Zeitpunkt also abnimmt. Dies ist also der Zeitpunkt, zu dem der Befall nach 2018 zum ersten mal nicht sichtbar wird. Dieser Zeitpunkt $t\approx 32,172$ liegt im $33.$ Jahr nach Beobachtungsbeginn und damit im Jahr 2022.

2.3

Strategien erläutern

$(\text{I})$

Bei der ersten Methode werden die einzelnen Jahreswerte für $t=29,$ $t=30,$ ..., jeweils stellvertretend für das gesamte Jahr 2018, 2019,..., verwendet und deren Mittelwert gebildet.

$(\text{II})$

Bei der zweiten Strategie wird der Mittelwert aller Funktionswerte von $k$ im betrachteten Intervall inklusive einer Stetigkeitskorrektur gebildet. Dieser bezieht neben den ganzzahligen $t$ -Werten auch die Bewegung innerhalb der Jahre mit ein.

Wert von $d_{\text{II}}$ bestimmen

Mit dem CAS kann das Integral berechnet werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

Es folgt: $d_{\text{II}} \approx 269,56$

Die beiden Werte $d_{\text{I}} \approx 272,10$ und $d_{\text{II}}\approx 269,56$ weichen nur geringfügig voneinander ab. Mit beiden Strategien ergibt sich für die Jahre von 2018 bis 2037 also eine zu erwartende durchschnittliche maximale Larvendichte pro Jahr von ca. $270$ Larven pro Kilogramm Zweige.