B1 - Analysis

Den Funktionen $v_1,v_2$ und $v_3$ sind folgende Funktionsgleichungen zugeordnet:

$v_1(t)=5\cdot \left(1- \mathrm{e}^{-0,4\cdot t}\right)$
$v_2(t)=4,5+\mathrm{e}^{-0,5\cdot t}\cdot \left(t-0,25t^2\right)$
$v_3(t)=3t\cdot \mathrm{e}^{-0,2\cdot t}$

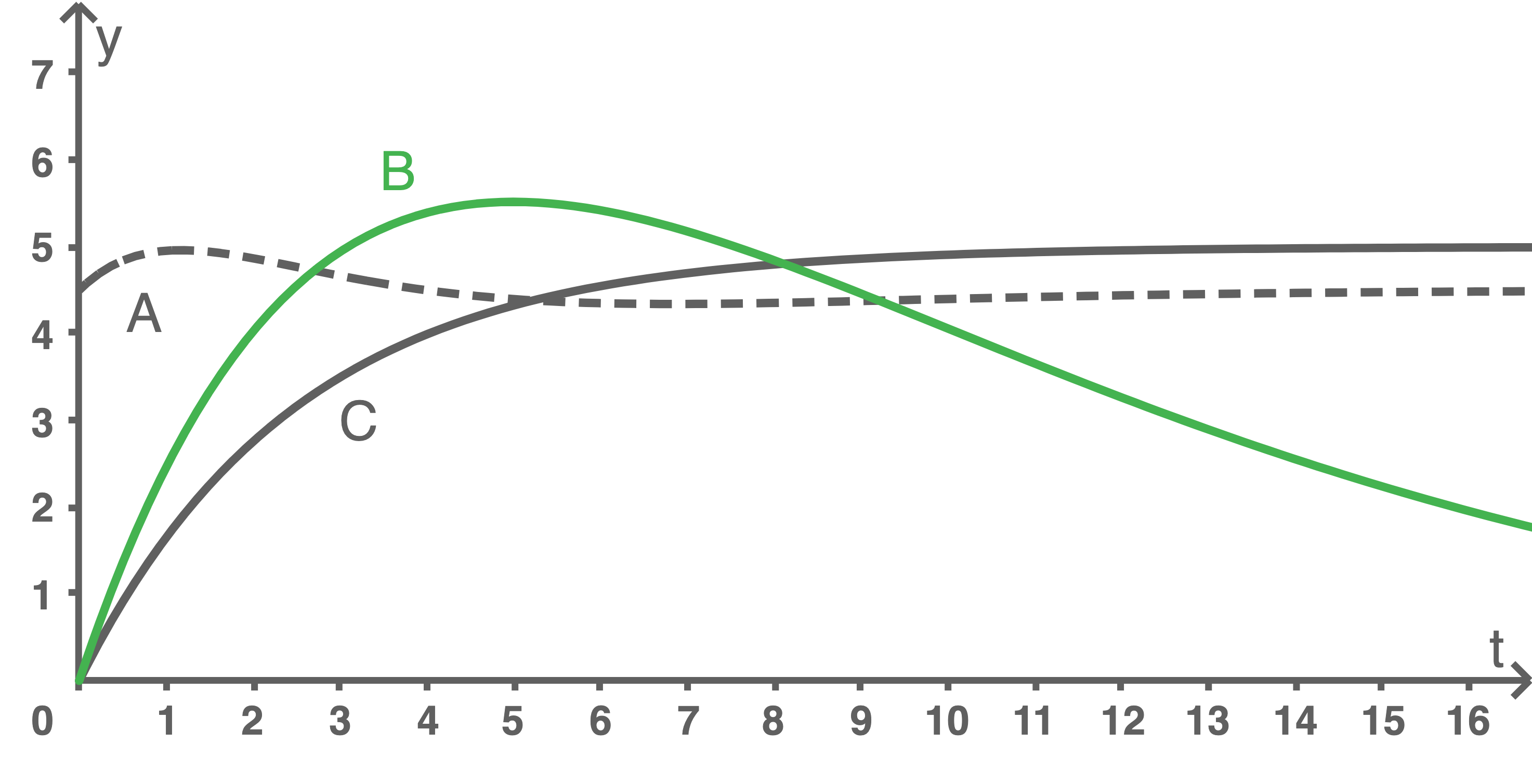
Material 1: Graphen A, B und C

1.1

In Material 1 sind drei Graphen $A, B$ und $C$ abgebildet, die zu den Funktionen $v_1$ , $v_2$ und $v_3$ gehören. Ordne den Funktionen die zugehörigen Graphen begründet zu.

(4 BE)

1.2

Berechne den Inhalt der Fläche zwischen dem Graphen von $v_1$ und der $t-$ Achse über dem Intervall $[0,10].$

(4 BE)

1.3

Zeige, dass die Funktion $v_2$ maximal zwei Extremstellen haben kann.

(4 BE)

Die Funktion $v_3$ gehört zu der Funktionenschar $f_k$ mit
$f_k(t)=3\cdot t\cdot \mathrm e^{-k\cdot t}, k\gt 0.$

2.1

Berechne mithilfe des Formansatzes $F_k(t)=(a+b\cdot t)\cdot \mathrm e^{-k\cdot t}$ mit $a, b\in\mathbb{R}$ eine Stammfunktionenschar $F_k$ von $f_k.$
$\bigg[$ zur Kontrolle: $F_k(t)= \left(-\dfrac{3}{k^2}-\dfrac{3}{k}\cdot t\bigg)\cdot \mathrm e^{-k\cdot t}\right]$

(5 BE)

2.2

Ermittle $\lim\limits_{x\to\infty}\displaystyle\int_{0}^{x}f_k(t)\;\mathrm dt.$

(3 BE)

2.3

Berechne in Abhängigkeit von $k$ die Nullstellen und die Hochpunkte der Scharkurven.
Die zweite Ableitung $\(f_k$ kann ohne Nachweis verwendet werden.
$\bigg[$ zur Kontrolle: $H\left(\dfrac{1}{k}\,\bigg \vert \,\dfrac{3}{\mathrm e\cdot k}\right)\bigg]$

(7 BE)

2.4

Bestimme die Ortskurve der Hochpunkte.

(2 BE)

Die drei Graphen $A,B$ und $C$ in Material 1 beschreiben die Geschwindigkeiten dreier Radfahrer $R_A,R_B$ und $R_C$ in Meter pro Sekunde $\left(\dfrac{m}{s}\right)$ in Abhängigkeit von der Zeit $t\geq 0$ in Sekunden $(s).$
Die Radfahrer befinden sich zur Zeit $t=0$ alle am gleichen Ort und fahren auf der gleichen Straße in die gleiche Richtung.

3.1

Beschreibe im Vergleich den Geschwindigkeitsverlauf der drei Radfahrer in den ersten $16$ Sekunden nach dem Start.

(4 BE)

3.2

Beurteile anhand des Materials ohne Verwendung einer Rechnung, welcher der drei Radfahrer $6$ Sekunden nach dem Start in Führung liegt.

(3 BE)

3.3

Die Beschleunigung ist die Änderungsrate der Geschwindigkeit.
Bestimme für den Radfahrer mit der Geschwindigkeit, die durch die Funktion $v_1$ beschrieben wird, die Beschleunigung fünf Sekunden nach dem Start.
Eine Angabe der Einheit ist nicht notwendig.

(2 BE)

3.4

Ermittle für den Radfahrer, dessen Geschwindigkeit durch die Funktion $v_3$ beschrieben wird, die in den ersten 16 Sekunden zurückgelegte Strecke sowie die zugehörige Durchschnittsgeschwindigkeit.

(3 BE)

3.5

Ermittle mithilfe des WTR den Inhalt der zwischen den Graphen von $v_1$ und $v_3$ eingeschlossenen Fläche. Deute den ermittelten Wert im Sachzusammenhang.

(5 BE)

3.6

Deute im Sachzusammenhang den Wert des Integrals $\displaystyle\int_{0}^{t_0}(v_1(t)-v_3(t))\;\mathrm dt$ für $t_0\gt 0,$ wenn dieser kleiner null, größer null bzw. gleich null ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Es gilt $v_{2}(0) = 4,5$ . Damit kann die Funktion $v_2$ anhand des $y-$ Achsenabschnitts dem Graphen $A$ zugeordnet werden.

Außerdem gilt $v_{1}(16) \approx 4,99$ . Damit lässt sich die Funktion $v_1$ anhand des zu $t=16$ gehörenden Wertes dem Graphen $C$ zuordnen.

Nach Ausschlussverfahren folgt jetzt: Die Funktion $v_3$ lässt sich dem Graphen $B$ zuordnen. Außerdem gilt hier $v_3(16)=1,96.$

1.2

Vollständigen Rechenweg anzeigen

$\displaystyle\int_{0}^{10}v_{1}(t)\;\mathrm dt \approx 37,73$

Damit beträgt der Flächeninhalt etwa $37,73\,\text{FE}.$

1.3

Notwendige Bedingung für Extremstellen anwenden:

$\mathrm{e}^{-0,5t} \cdot (0,125t^2 - t +1)=0$

Rechenweg anzeigen

Da $\mathrm{e}^{-0,5t}\gt 0,$ muss nach dem Satz vom Nullprodukt die quadratische Gleichung $(0,125t^2 - t +1)$ den Wert null annehmen.

Da quadratische Funktionen maximal zwei Nullstellen haben, hat $\(v_{2}$ maximal zwei Nullstellen und $v_{2}(t)$ folglich maximal zwei Extremstellen.

2.1

Da $F_{k}(t)$ eine Stammfunktion von $f_{k}(t)$ ist, muss Folgendes gelten:

Vollständigen Rechenweg anzeigen

$\( \begin{array}[t]{rll} f_{k}(t) &=& F_{k}$

Damit die Gleichung gilt, müssen die Terme, die $t$ enthalten, den gleichen Wert annehmen:

$\begin{array}[t]{rll} 3t&=& - k \cdot b \cdot t&\quad \scriptsize \mid\; :(k \cdot t) \\[5pt] \dfrac{3}{k}&=& -b& \quad \scriptsize \mid\; \cdot (-1) \\[5pt] -\dfrac{3}{k}&=& b \\ \end{array}$

Mit $b = -\dfrac{3}{k}$ folgt:

$\begin{array}[t]{rll} 3t& =& -\dfrac{3}{k} - k \cdot a + 3t& \quad \scriptsize \mid\; -3t \\[5pt] 0 & =& -\dfrac{3}{k} - k \cdot a & \quad \scriptsize \mid \; + \frac{3}{k} \\[5pt] \dfrac{3}{k}& =& - k \cdot a & \quad \scriptsize \mid\; :(-k) \\[5pt] -\dfrac{3}{k^2}&=& a \\ a&=& -\dfrac{3}{k^2} \end{array}$

Damit gilt dann für $F_{k}(t)$ :

$F_{k}(t) = \left(-\dfrac{3}{k^2} - \dfrac{3}{k} \cdot t \right) \cdot \mathrm{e}^{-kt}$

2.2

$\lim\limits_{x\to\infty} \displaystyle\int_{0}^{x}f_{k}(t)\;\mathrm dt$

Umformungen anzeigen

$F_k(x)=\left(-\dfrac{3}{k^2}-\dfrac{3}{k}\cdot x\right)\cdot \mathrm e^{-kx}$

Für $x\rightarrow \infty$ gilt:

$\underbrace{\underbrace{\left(-\dfrac{3}{k^2} - \dfrac{3}{k} \cdot x \right)}_{\rightarrow - \infty} \cdot \underbrace{ \mathrm{e}^{-kx}}_{\rightarrow 0}}_{\to 0}\rightarrow 0$

Da der Term $\mathrm e^{-kx}$ für $x \to \infty$ dominiert und gegen null verläuft, verläuft der gesamte Term gegen null.

Damit gilt:

$\lim\limits_{x\to\infty} \displaystyle\int_{0}^{x}f_{k}(t)\;\mathrm dt = \dfrac{3}{k^2}$

Rechenweg anzeigen

2.3

Es gilt:

$f_{k}(t) = 3t \cdot \mathrm{e}^{-kt}$

$\( f_{k}$

$\(f_{k}$

Nullstellen berechnen

$\begin{array}[t]{rll} f_{k}(t)&=& 0&\quad \scriptsize \\[5pt] 3t \cdot \mathrm{e}^{-kt}&=& 0& \quad \scriptsize \mid \; :(3\cdot \mathrm{e}^{-kt}) \\[5pt] t& =& 0& \end{array}$

Damit besitzen die Scharkurven eine von $k$ unabhängige Nullstelle $N$ bei $t=0$ .

Hochpunkte ermitteln

1. Schritt: Notwendige Bedingung für Extremstellen prüfen

Rechenweg anzeigen

$\dfrac{1}{k}=t$

2. Schritt: Hinreichende Bedingung für Hochpunkte prüfen

$\(\begin{array}[t]{rll} f_{k}$

Da $k \gt 0$ und $\mathrm{e} \gt 0$ gilt: $\( \quad f_{k}$ .

Damit befindet sich bei $H = \left(\dfrac{1}{k} \,\bigg \vert \, f_{k}\left(\dfrac{1}{k}\right) \right) = \left(\dfrac{1}{k} \,\bigg \vert \, \dfrac{3}{\mathrm{e} \cdot k} \right)$ ein Hochpunkt der Scharkurven.

2.4

Es gilt $k \gt 0$ und $t= \dfrac{1}{k}.$

Daraus folgt: $k=\dfrac{1}{t}$ und $t \gt 0.$

Durch einsetzen von $k = \dfrac{1}{t} \;$ in $\; y = \dfrac{3}{\mathrm{e} \cdot k}$ ergibt sich:

$y=\dfrac{3}{\mathrm{e} \cdot k}=\dfrac{3}{\mathrm{e}} \cdot t$

Somit gilt für die Ortskurve der Hochpunkte:

$O(t) = \dfrac{3}{\mathrm{e}} \cdot t \;$ für $t \gt 0$

3.1

Radfahrer $A$ startet direkt mit $4,5 \,\frac{\text{m}}{\text{s}}$ , wird für wenige Sekunden schneller und fährt danach mit nahezu konstanter Geschwindigkeit von ungefähr $4,5 \,\frac{\text{m}}{\text{s}}$ bis zum Ende durch.

Radfahrer $B$ startet mit $0 \,\frac{\text{m}}{\text{s}}$ , beschleunigt schnell und erreicht nach $5$ Sekunden seine maximale Geschwindigkeit. Diese fällt anschließend wieder stark ab, sodass er gegen Ende am langsamsten fährt.

Radfahrer $C$ hingegen startet bei $0 \,\frac{\text{m}}{\text{s}}$ und beschleunigt nicht so schnell wie Radfahrer $B$ . Während des gesamten Verlaufs, steigert er seine Geschwindigkeit, sodass er nach $16$ Sekunden mit nahezu konstanter Geschwindigkeit von knapp $5 \,\frac{\text{m}}{\text{s}}$ am schnellsten ist.

3.2

Zu betrachten ist die Fläche, die die einzelnen Graphen mit der $t-$ Achse auf dem Intervall $[0;6]$ einschließen. Damit ist sofort ersichtlich, dass Radfahrer $C$ nach $6$ Sekunden der Letzte ist.

Um nun den führenden Radfahrer zwischen Fahrer $A$ und Fahrer $B$ zu ermitteln, wird die Fläche betrachtet, die die Graphen $A$ und $B$ einschließen. Beim größeren Teil dieser Fläche befindet sich der Graph $A$ über dem Graphen $B$ . Somit liegt Radfahrer $A$ nach $6$ Sekunden in Führung.

3.3

Für die Ableitung von $v_{1}(t)$ gilt:

$\(v_{1}$

Die Beschleunigung des Radfahrers $C$ liegt nach $5$ Sekunden bei etwa $0,27 \, \frac{\text{m}}{\;\text{s}^2}.$

3.4

Aus Aufgabe 2.1 erhält man mit $k = 0,2$ die Stammfunktion für $v_3(t)$ .

Zurückgelegte Strecke berechnen

$\displaystyle\int_{0}^{16}v_{3}(t)\;\mathrm dt$ $= \left[\left(-75 - 15 \cdot t \right) \cdot \mathrm{e}^{-0,2t} \right]^{16}_{0}$ $\approx 62,16 \; [\text{m}]$

Durchschnittsgeschwindigkeit

$\dfrac{1}{16} \cdot \displaystyle\int_{0}^{16}v_{3}(t)\;\mathrm dt \approx 3,88$ $\;\left[\frac{\text{m}}{\; \text{s}^2} \right]$

Der Radfahrer von $v_3$ hat nach $16$ Sekunden ca. $62,16 \,\text{m}$ zurückgelegt und hatte damit eine Durchschnittsgeschwindigkeit von $3,88 \; \frac{\text{m}}{\text{s}}$ .

3.5

Flächeninhalt bestimmen

Die Schnittstellen von $v_1$ und $v_3$ können aus dem Schaubild entnommen werden: $\; t_{1} = 0$ und $t_{2} \approx 8,1$

Damit lässt sich die Fläche zwischen den Graphen von $v_1$ und $v_3$ durch das Integral über die Differenz der beiden Funktionen berechnen.

Mit dem WTR folgt:

Vollständigen Rechenweg anzeigen

$\displaystyle\int_{0}^{8,1}v_3(t)-v_1(t)\;\mathrm dt \approx7,62$

Wert deuten

Der Inhalt der Fläche zwischen $v_{1}$ und $v_{3}$ beträgt etwa $7,62 \;[ \,\text{FE}]$ .

Nach ca. $8,1$ Sekunden haben die beiden Radfahrer die gleiche Geschwindigkeit. Da beide gleichzeitig und am gleichen Ort starten, hat Radfahrer $B$ zu diesem Zeitpunkt einen Vorsprung von ungefähr $7,62\,\text{m}$ zum Radfahrer $C.$

3.6

Ist der Integralwert größer null, dann bedeutet dies im Sachzusammenhang, dass der Radfahrer von $v_{1}$ mehr Strecke im betrachteten Zeitraum vom Start bis $t_0$ zurücklegt als der Radfahrer von $v_{3}$ . Der Integralwert gibt dann den Vorsprung des Radfahrers von $v_1$ in Metern an.

Ist der Integralwert kleiner null, dann bedeutet dies im Sachzusammenhang, dass der Radfahrer von $v_{3}$ mehr Strecke im betrachteten Zeitraum zurücklegt, als der Radfahrer von $v_{1}$ . Der Integralwert gibt dann den Vorsprung des Radfahrers von $v_3$ in Metern an.

Ist der Integralwert gleich null, dann beutet dies im Sachzusammenhang, dass beide Radfahrer im betrachteten Zeitraum genau gleich viel Strecke zurückgelegt haben.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?