B1 - Analysis
1
Eine Flasche Wasser wird in einem Kühlschrank auf 8 °C abgekühlt. An einem Sommertag wird diese entnommen und in ein Zimmer mit 30 °C Raumtemperatur gestellt. 10 Minuten später hat sich das Wasser bereits auf 21,9 °C erwärmt. Im Modell wird davon ausgegangen, dass sich die Raumtemperatur nicht verändert.
Der Temperaturverlauf der Erwärmung des Wassers kann durch die Funktion  beschrieben werden mit:
beschrieben werden mit:
 Dabei bedeutet:
Dabei bedeutet:
Zeit in Minuten nach Entnahme aus dem Kühlschrank
Temperatur des Wassers in °C zum Zeitpunkt
Temperatur des Wassers in °C zum Zeitpunkt
Raumtemperatur in °C
1.1
Nenne die Werte für die Parameter  und
und 
Ermittle auf vier Nachkommastellen gerundet den Wert für den Parameter und gib die zugehörige Funktionsgleichung
und gib die zugehörige Funktionsgleichung  an.
[Zur Kontrolle:
an.
[Zur Kontrolle:  ]
]
Verwende im Folgenden die Funktionsgleichung Ermittle auf vier Nachkommastellen gerundet den Wert für den Parameter
(4 BE)
1.2
Berechne, um wie viel Prozent die Temperatur des Wassers in den ersten  Minuten nach Entnahme aus dem Kühlschrank zunimmt.
Minuten nach Entnahme aus dem Kühlschrank zunimmt.
(2 BE)
1.3
Berechne den Wert des Terms  und deute das Ergebnis im Sachzusammenhang.
und deute das Ergebnis im Sachzusammenhang.
(4 BE)
1.4
Begründe mithilfe des Funktionsterms, dass gilt:  Erläutere diesen Grenzwert im Sachzusammenhang.
Erläutere diesen Grenzwert im Sachzusammenhang.
(3 BE)
1.5
Berechne, mit welcher Geschwindigkeit sich das Wasser zum Zeitpunkt der Entnahme aus dem Kühlschrank erwärmt, und berechne, wann sich diese Erwärmungsgeschwindigkeit halbiert hat.
Zeige, dass gemäß der Modellierung durch die Funktion  die Erwärmungsgeschwindigkeit im Zeitverlauf abnimmt, jedoch nie null wird.
die Erwärmungsgeschwindigkeit im Zeitverlauf abnimmt, jedoch nie null wird.
(9 BE)
1.6
Eine Funktion  beschreibt ein begrenztes Wachstum, wenn die Wachstumsgeschwindigkeit proportional zur Differenz aus Sättigungsgrenze
beschreibt ein begrenztes Wachstum, wenn die Wachstumsgeschwindigkeit proportional zur Differenz aus Sättigungsgrenze  und dem aktuellen Bestand ist, d.h., wenn
und dem aktuellen Bestand ist, d.h., wenn  gilt.
gilt.
Zeige unter Verwendung des Kontrollergebnisses für aus Aufgabe 1.1, dass die Funktion
aus Aufgabe 1.1, dass die Funktion  ein begrenztes Wachstum beschreibt.
ein begrenztes Wachstum beschreibt.
Deute den Wert für im Sachzusammenhang.
im Sachzusammenhang.
Zeige unter Verwendung des Kontrollergebnisses für
Deute den Wert für
(4 BE)
2
Gegeben ist die Funktionenschar  mit
mit  , wobei
, wobei  und
und  gilt. Im Material sind zwei ausgewählte Graphen der Schar abgebildet.
gilt. Im Material sind zwei ausgewählte Graphen der Schar abgebildet.
2.1
Zeige, dass alle Graphen der Schar dieselbe Nullstelle und den denselben  -Achsenabschnitt besitzen, und gib die Schnittpunkte mit den oordinatenachsen an.
-Achsenabschnitt besitzen, und gib die Schnittpunkte mit den oordinatenachsen an.
(3 BE)
2.2
Die Graphen von  nähern sich für
nähern sich für  der
der  -Achse an.
-Achse an.
Begründe dieses Verhalten anhand des Funktionsterms. Die beiden im Material abgebildeten Graphen unterscheiden sich bei der Annäherung an die -Achse.
-Achse.
Erkläre diesen Unterschied anhand des Funktionsterms.
Begründe dieses Verhalten anhand des Funktionsterms. Die beiden im Material abgebildeten Graphen unterscheiden sich bei der Annäherung an die
Erkläre diesen Unterschied anhand des Funktionsterms.
(5 BE)
2.3
Ermittle die Gleichung der Ableitungsfunktion  und zeige, dass gilt:
und zeige, dass gilt:

(4 BE)
2.4
Berechne die möglichen Extremstellen von  Die Untersuchung der notwendigen Bedingung ist hierbei ausreichend.
Gib die Skalierung der Achsen im Material an.
Die Untersuchung der notwendigen Bedingung ist hierbei ausreichend.
Gib die Skalierung der Achsen im Material an.
Bestimme für beide Graphen und
und  im Material die zugehörigen Werte des Parameters
im Material die zugehörigen Werte des Parameters 
Bestimme für beide Graphen
(6 BE)
2.5
An der Stelle  besitzen die Graphen der Funktionenschar
besitzen die Graphen der Funktionenschar  für gerade Werte von
für gerade Werte von  einen Extrempunkt und für ungerade Werte von
einen Extrempunkt und für ungerade Werte von  einen Sattelpunkt.
Begründe diese Aussage.
einen Sattelpunkt.
Begründe diese Aussage.
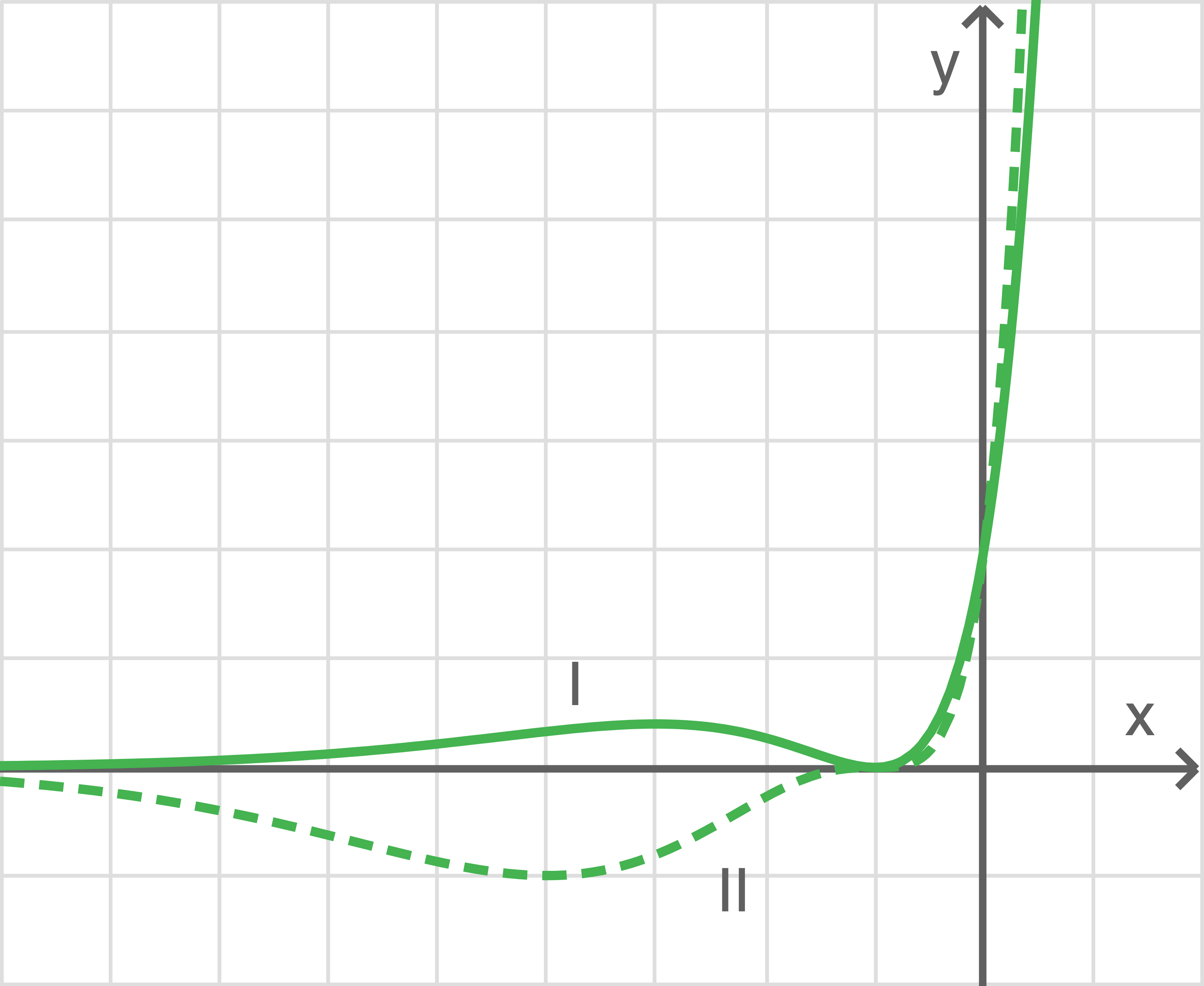

Material 1
(6 BE)
1.1
Parameter benennen
Die Parameter  und
und  können aus dem Aufgabentext abgelesen werden: Die Raumtemperatur beträgt
können aus dem Aufgabentext abgelesen werden: Die Raumtemperatur beträgt  und zu Beginn, also nach Entnahme aus dem Kühlschrank, hat das Wasser die Temperatur
und zu Beginn, also nach Entnahme aus dem Kühlschrank, hat das Wasser die Temperatur  .
Parameter
.
Parameter  bestimmen
Durch Einsetzen von
bestimmen
Durch Einsetzen von  und der Temperatur nach 10 Minuten ergibt sich:
Für die Funktionsgleichung gilt somit:
und der Temperatur nach 10 Minuten ergibt sich:
Für die Funktionsgleichung gilt somit:

1.2
Das Wasser hat sich in den ersten  Minuten um
Minuten um  Grad erwärmt.
Die prozentuale Zunahme folgt mit
Grad erwärmt.
Die prozentuale Zunahme folgt mit 
1.3
Wert des Terms berechnen
Ergebnis deuten
Das Wasser hatte in den ersten  Minuten eine durchschnittliche Temperatur von
Minuten eine durchschnittliche Temperatur von 
1.4
Grenzwert begründen
Da  gilt, muss dies auch für die gesamte Funktion gelten:
gilt, muss dies auch für die gesamte Funktion gelten:
 Grenzwert erläutern
Im Sachzusammenhang gibt der Grenzwert die Temperatur an, welcher sich das Wasser mit der Zeit annähert. Das Wasser passt sich also der Raumtemperatur an und wird nach genügend langer Zeit näherungsweise
Grenzwert erläutern
Im Sachzusammenhang gibt der Grenzwert die Temperatur an, welcher sich das Wasser mit der Zeit annähert. Das Wasser passt sich also der Raumtemperatur an und wird nach genügend langer Zeit näherungsweise  annehmen.
annehmen.
1.5
Erwärmungsgeschwindigkeit berechnen
Die Geschwindigkeit, mit welcher sich das Wasser erwärmt, entspricht der ersten Ableitung:
 Zum Zeitpunkt der Entnahme beträgt die Erwärmungsgeschwindigkeit somit:
Zum Zeitpunkt der Entnahme beträgt die Erwärmungsgeschwindigkeit somit:
 Zeitpunkt der Halbierung berechnen
Zeitpunkt der Halbierung berechnen
![\(\begin{array}[t]{rll}
w(t)&=& \dfrac{2,2}{2} & \\[5pt]
2,2\cdot \mathrm e^{-0,1t}&=&1,1 &\quad \scriptsize \mid\; :2,2 \\[5pt]
\mathrm e^{-0,1t}&=& 0,5 &\quad \scriptsize \mid\; \ln() \\[5pt]
-0,1t &=& \ln(0,5)&\quad \scriptsize \mid\; :(-0,1) \\[5pt]
t&\approx& 6,93
\end{array}\)](https://mathjax.schullv.de/3b16d6c8d72d0893dadc4cd81c47b0a9d9c70d1c8aa86cbb14259365e4f8cb75?color=5a5a5a) Nach etwa
Nach etwa  Minuten hat sich die Erwärmungsgeschwindigkeit halbiert.
Erwärmungsverlauf begründen
Aus
Minuten hat sich die Erwärmungsgeschwindigkeit halbiert.
Erwärmungsverlauf begründen
Aus  folgt auch
folgt auch  gelten.
Somit wird die Erwärmungsgeschwindigkeit nie kleiner oder gleich null.
Die Ableitung
gelten.
Somit wird die Erwärmungsgeschwindigkeit nie kleiner oder gleich null.
Die Ableitung  beschreibt die Änderungsrate der Erwärmungsgeschwindigkeit.
Da
beschreibt die Änderungsrate der Erwärmungsgeschwindigkeit.
Da  ist, nimmt
ist, nimmt  streng monoton ab.
Die Erwärmungsgeschwindigkeit nimmt also immer ab, bleibt aber stets positiv.
streng monoton ab.
Die Erwärmungsgeschwindigkeit nimmt also immer ab, bleibt aber stets positiv.
1.6
Begrenztes Wachstum zeigen
Setze  , die Schranke
, die Schranke  und die Funktion
und die Funktion  in die Gleichung ein:
in die Gleichung ein:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/e736760d7d45fe7baefca811142284df6e920d66e8e74630677840b21d6e6a81?color=5a5a5a) Somit beschreibt die Funktion
Somit beschreibt die Funktion  ein begrenztes Wachstum.
Wert für
ein begrenztes Wachstum.
Wert für  deuten
Im Sachzusammenhang beschreibt
deuten
Im Sachzusammenhang beschreibt  die Erwärmungsgeschwindigkeit zu jedem Zeitpunkt mit jeweiliger Temperaturdifferenz zwischen Wasser- und Raumtemperatur. Das Wasser erwärmt sich also immer um
die Erwärmungsgeschwindigkeit zu jedem Zeitpunkt mit jeweiliger Temperaturdifferenz zwischen Wasser- und Raumtemperatur. Das Wasser erwärmt sich also immer um  dieser Temperaturdifferenz.
dieser Temperaturdifferenz.
2.1
Gleichheit der Nullstellen zeigen
![\(\begin{array}[t]{rll}
f_n(x) &=& 0 \\[5pt]
(x+1)^n\cdot\mathrm e^x &=& 0 \quad \scriptsize \mid\;:\mathrm e^x\\[5pt]
(x+1)^n &=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1bdf9030b80ae53bf0a06f25e40868033ea27bee076761e42a6e6a8a140f0c29?color=5a5a5a) Die Nullstelle folgt mit
Die Nullstelle folgt mit  und ist somit unabhängig von
und ist somit unabhängig von  .
Gleichheit des
.
Gleichheit des  -Achsenabschnitts zeigen
-Achsenabschnitts zeigen
 Der
Der  -Achsenabschnitt ist also unabhängig von
-Achsenabschnitt ist also unabhängig von  .
Somit besitzen alle Graphen der Schar ihre Nullstelle bei
.
Somit besitzen alle Graphen der Schar ihre Nullstelle bei  und ihren
und ihren  -Achsenabschnitt bei
-Achsenabschnitt bei  Schnittpunkte angeben
Der Schnittpunkt der Schar mit der
Schnittpunkte angeben
Der Schnittpunkt der Schar mit der  -Achse entspricht den Koordinaten der Nullstelle:
-Achse entspricht den Koordinaten der Nullstelle:  Der Schnittpunkt mit der
Der Schnittpunkt mit der  -Achse folgt direkt aus dem
-Achse folgt direkt aus dem  -Achsenabschnitt:
-Achsenabschnitt: 
2.2
Verhalten für  erklären
Es gilt
erklären
Es gilt  . Da der Faktor
. Da der Faktor  das Verhalten der Graphen der Funktionenschar für
das Verhalten der Graphen der Funktionenschar für  dominiert, nähern sich die Graphen der
dominiert, nähern sich die Graphen der  -Achse an.
-Achse an.
Unterschied erklären Ob die Annäherung eines Graphen der Funkionenschar an die -Achse aus dem zweiten oder aus dem dritten Quadranten erfolgt, hängt vom Vorfaktor
-Achse aus dem zweiten oder aus dem dritten Quadranten erfolgt, hängt vom Vorfaktor  ab.
ab.
Für gerade strebt für
strebt für  der Faktor
der Faktor  gegen
gegen  . Somit erfolgt die Annäherung aus dem zweiten Quadranten.
. Somit erfolgt die Annäherung aus dem zweiten Quadranten.
Für ungerade strebt für
strebt für  der Faktor
der Faktor  gegen
gegen  . Somit erfolgt die Annäherung aus dem dritten Quadranten.
. Somit erfolgt die Annäherung aus dem dritten Quadranten.
Unterschied erklären Ob die Annäherung eines Graphen der Funkionenschar an die
Für gerade
Für ungerade
2.3
Mit der Produktregel folgt:
2.4
Mögliche Extremstellen berechnen
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f_n](https://mathjax.schullv.de/0494c91be16a36f5be51db71b188af539c16aba6f46d883cbfb1f9fe988d0ac3?color=5a5a5a) Da
Da  gilt, folgt mit dem Satz vom Nullprodukt:
gilt, folgt mit dem Satz vom Nullprodukt:
 und
und  Möglichen Extremstellen von
Möglichen Extremstellen von  sind somit
sind somit  und
und  Achsenbeschriftung angeben
Achsenbeschriftung angeben
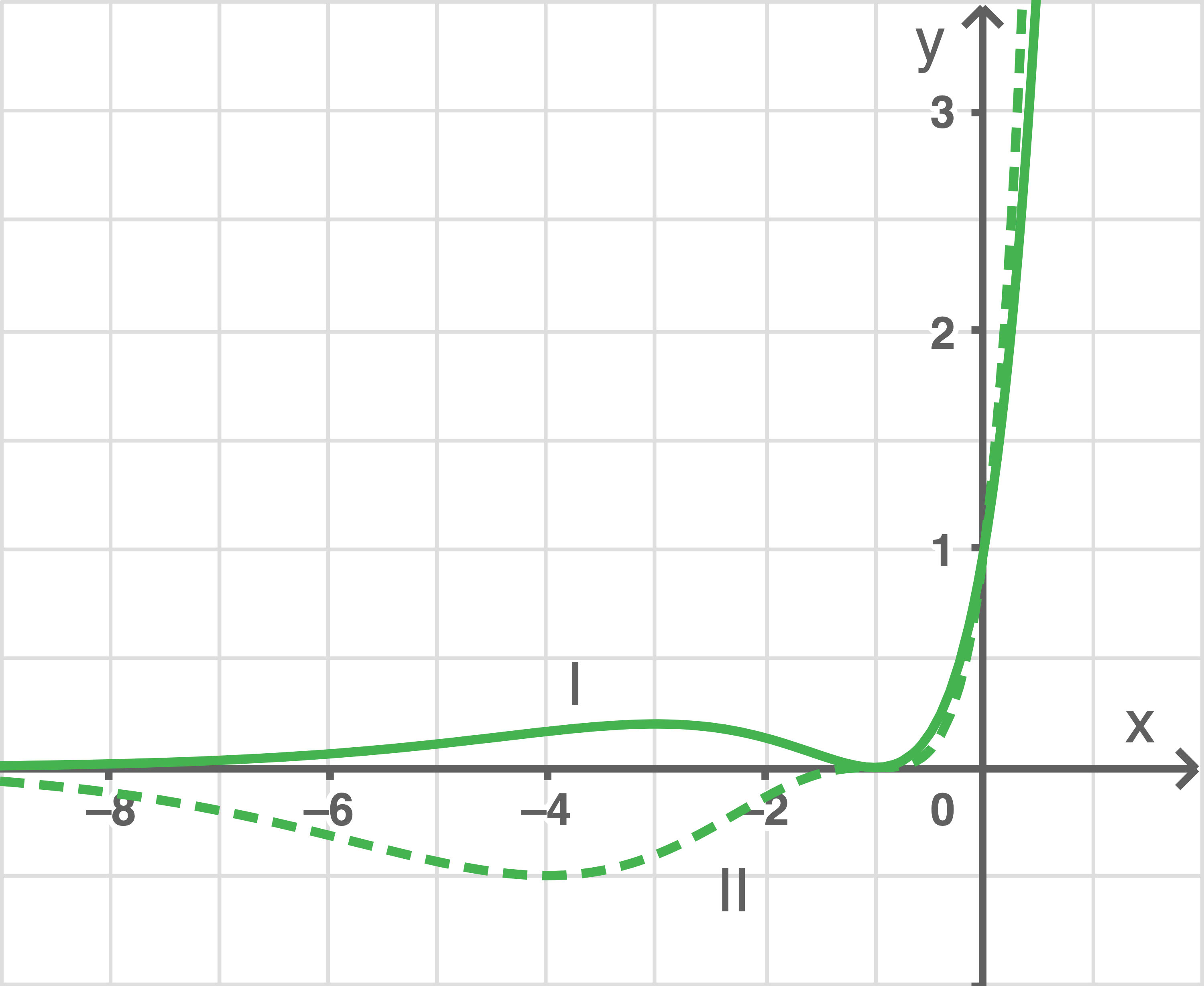 Parameter
Parameter  bestimmen
Die
bestimmen
Die  -Koordinaten der Extrempunkte der beiden Graphen können aus dem Schaubild abgelesen werden.
Graph
-Koordinaten der Extrempunkte der beiden Graphen können aus dem Schaubild abgelesen werden.
Graph  besitzt seinen Hochpunkt bei
besitzt seinen Hochpunkt bei  , damit gilt
, damit gilt  und folglich
und folglich  Graph
Graph  besitzt seinen Tiefpunkt bei
besitzt seinen Tiefpunkt bei  , damit gilt
, damit gilt  und somit
und somit 

2.5
Der Funktionsterm der ersten Ableitungsfunktion lautet:
 In der Nähe von
In der Nähe von  ist der Faktor
ist der Faktor  positiv, da
positiv, da  . Ebenfalls gilt
. Ebenfalls gilt  Somit genügt es, den Faktor
Somit genügt es, den Faktor  zu betrachten.
Dieser Faktor hat an der Stelle
zu betrachten.
Dieser Faktor hat an der Stelle  für gerade Werte von
für gerade Werte von  eine Nullstelle mit Vorzeichenwechsel und somit einen Extrempunkt.
Für ungerade Werte von
eine Nullstelle mit Vorzeichenwechsel und somit einen Extrempunkt.
Für ungerade Werte von  eine Nullstelle ohne Vorzeichenwechsel (Sattelpunkt).
eine Nullstelle ohne Vorzeichenwechsel (Sattelpunkt).