B2 - Analysis

Mediziner und Biologen untersuchen die Auswirkungen von Antibiotika auf das Wachstum von Bakterienbeständen. Bakterien vermehren sich exponentiell. Fügt man diesen Bakterien ein Antibiotikum hinzu, wird das Wachstum des Bakterienbestands gehemmt. Das Antibiotikum bewirkt, dass die Bakterien absterben und der Bakterienbestand sich schlussendlich wieder dem Wert null annähert; man spricht in diesem Zusammenhang auch von vergiftetem Wachstum.
Mit den Funktionen der Schar $f_a$ mit $f_a(t)=e^{a \cdot t-0,3 \cdot t^2}$ , $t \geq 0, a \geq 0$ , kann der Bakterienbestand in einem Organismus dargestellt werden, wobei $t$ die Zeit in Tagen nach Beobachtungsbeginn und $f_a(t)$ die Anzahl der Bakterien in Tausend angibt.

1.1

Begründe, dass die Funktionen der Schar $f_a$ keine Nullstellen besitzen.

(2 BE)

1.2

Gib das Grenzwertverhalten der Funktionen der Schar $f_a$ für $t\rightarrow + \infty$ an und begründe dein Ergebnis anhand des Funktionsterms.

(3 BE)

1.3

Bestätige, dass jeder Graph der Schar $f_a$ einen Hochpunkt im Punkt $HP \left(\dfrac{5}{3}a\, |\, \mathrm{e}^{\frac{5}{6}a^2}\right)$ hat, und berechne die Funktionsgleichung der Ortskurve der Hochpunkte.

(8 BE)

1.4

Erkläre für $h\gt 0$ die Aussagen der Zeilen $(1)$ bis $(3)$ und deute das Ergebnis in Zeile $(3)$ geometrisch.

$(1)$ $f_a\left(\dfrac{5}{3}a+h \right)=e^{\frac{5}{6}a^2-0,3h^2}$

$(2)$ $f_a\left(\dfrac{5}{3}a-h \right)=e^{\frac{5}{6}a^2-0,3h^2}$

$(3)$ $\Rightarrow f_a\left(\dfrac{5}{3}a+h \right) = \left( \dfrac{5}{3}a-h \right)$

(5 BE)

1.5

Zeige, dass die Graphen zweier beliebiger Funktionen der Schar $f_a$ genau einen gemeinsamen Punkt besitzen, und bestimme diesen.

(4 BE)

Die Mediziner und Biologen analysieren unter Laborbedingungen einen Bakterienbestand, der durch die Funktion $f_a$ mit $a = 2,7$ beschrieben werden kann.

2.1

Skizziere den Graphen von $f_{2,7}$ und den Graphen der zugehörigen Stammfunktion $F_{2,7}$ mit $F_{2,7}(0)=0$ jeweils in ein geeignet skaliertes Koordinatensystem und erläutere die Bedeutung des Hochpunkts des Graphen von $f_{2,7}$ für den Graphen der Stammfunktion.

(5 BE)

2.2

Formuliere unter Bezug auf den Sachzusammenhang einen geeigneten Ansatz zur Berechnung des Zeitpunkts, ab dem man (bei Modellierung mit der Funktion $f_{2,7}$ ) davon ausgehen kann, dass keine Bakterien mehr vorhanden sind.
Bestimme diesen Zeitpunkt und erläutere das Ergebnis.

(3 BE)

2.3

Untersuche, zu welchem Zeitpunkt die Zunahme des Bakterienbestands am größten ist.

(4 BE)

Der Mittelwert $m$ der Funktionswerte $g(x)$ einer Funktion $g$ im Intervall $[a;b]$ kann durch die Formel $m =\dfrac{1}{b-a}\cdot \displaystyle\int_{a}^{b} g(x)\;\mathrm {dx} \,$ berechnet werden.
Für die Integration von $f_{2,7}$ muss auf Näherungsverfahren zurückgegriffen werden.

2.4

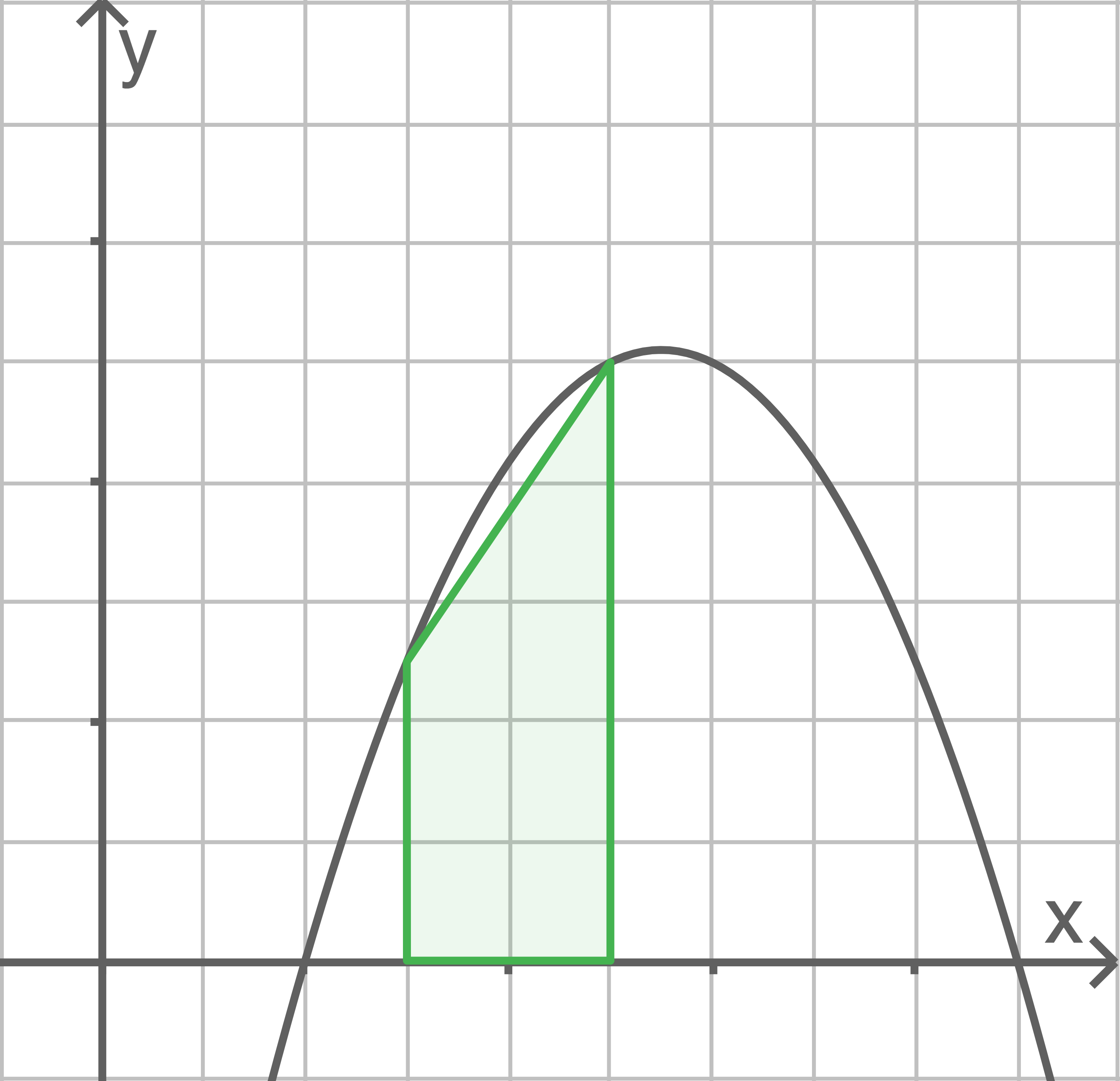
Eine Näherung für den Mittelwert der Anzahl an Bakterien während des zweiten Tages benutzt die Berechnung einer einzigen Trapezfläche wie für den Graphen einer anderen Funktion als Beispiel in Material 1 dargestellt.
Berechne auf diese Weise einen Näherungswert für die mittlere Anzahl an Bakterien während des zweiten Tages nach Beobachtungsbeginn.

Material 1: Trapezfläche

(3 BE)

2.5

Begründe für die Funktion $f_{2,7},$ dass es genau zwei Intervalle $[a;b]$ der Länge $b-a = 1$ gibt, in denen der Näherungswert durch die Trapezfläche gleich dem exakten Wert für den Mittelwert $m$ für das jeweilige Intervall ist.
Hinweis: Die Intervalle enthalten jeweils eine Wendestelle.

(4 BE)

2.6

Bestimme die mittlere Anzahl an Bakterien während des zweiten Tages, indem du den Wert des zugehörigen Integrals näherungsweise als Untersumme über fünf Rechtecke gleicher Breite ermittelst.

(4 BE)

2.7

Beschreibe eine mögliche Vorgehensweise, mit der die Genauigkeit des Näherungswertes aus Aufgabe 2.6 verbessert werden kann.

(2 BE)

Ein Arzneimittel wird als Tablette produziert und enthält neben dem Antibiotikum weitere Inhaltsstoffe. Die Tablette ist ein rotationssymmetrischer Körper. Die obere Randkurve der Querschnittsfläche der Tablette kann durch den Graphen der Funktion $h$ mit $h(x) = 0,5 \cdot \sqrt{1-x^2}\,$ beschrieben werden.
Eine Einheit im Koordinatensystem entspricht einem Zentimeter.

In $0,01\,\text{cm}^3$ einer Tablette befinden sich $2\,\text{mg}$ des Antibiotikums.
Bestimme, wie viel $\text{mg}$ des Antibiotikums eine Tablette enthält.

(4 BE)

1.1

Die Funktion $f_a$ ist eine Exponentialfunktion, die für alle Werte im Exponenten positiv ist, nie null wird und somit keine Nullstellen besitzt.

1.2

Grenzwertverhalten der Funktion der Schar $f_a$ für $t\rightarrow \infty$ :

Es gilt $t\rightarrow \infty$ für $g_a$ mit $g_a(t)=at-0,3t^2,\; t\geq 0,\; a\gt 0$ :
Für $t\rightarrow\infty$ verläuft $g_a(t)\rightarrow -\infty$ , weil $g_a$ eine nach unten geöffnete Parabel darstellt.
Da $g_a(t)$ der Exponent von $\mathrm e$ in $f_a(t)$ ist verläuft $f_a(t)\rightarrow 0$ mit $t\rightarrow \infty$ .

1.3

Hinreichende Bedingung für einen Hochpunkt: $\(f_a$ und $\(f_a$

$t= \dfrac{5}{3}a$

Vollständige Lösung anzeigen

$\( f_a$

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} f_a\bigg(\dfrac{5}{3}a\bigg)& = &\mathrm e^{a \cdot (\frac{5}{3}a)-0,3 \cdot (\frac{5}{3}a)^2}\quad \scriptsize\;\\[5pt] & = &\mathrm e^{\frac{5}{3}a^2- \frac{5}{6}a^2}\quad \scriptsize\;\\[5pt] & = &\mathrm e^{\frac{5}{6}a^2} \end{array}$

Jeder Graph der Schar $f_a$ hat im Punkt $HP \left(\frac{5}{3}a\, \,\mid \, \, \mathrm{e}^{\frac{5}{6}a^2}\right)$ einen Hochpunkt.

Funktionsgleichung der Ortskurve der Hochpunkte:

$t$ nach $a$ umformen:

$t=\dfrac{5}{3}a\Leftrightarrow a=\dfrac{3}{5}t$

$a$ in $y$ einsetzen:

$\begin{array}[t]{rll} y& = & \mathrm e^{\frac{5}{6}(\frac{3}{5}t)^2} & = &\mathrm e^{\frac{3}{10}t^2} \end{array}$

1.4

(1)

Es wird der Funktionswert an einer beliebigen Stelle im Abstand $h$ rechts der Extremstelle berechnet.

(2)

Es wird der Funktionswert an einer beliebigen Stelle im Abstand $h$ links der Extremstelle berechnet.

(3)

Der Funktionswert an einer belieben Stelle im Abstand $h$ rechts der Extremstelle ist gleich dem Funktionswert links der Extremstelle im selben Abstand $h$ . Dadurch wird klar, dass die Graphen der Funktionen der Schar $f_a$ zu einer Parallelen zur $y$ -Achse, die durch den Hochpunkt verläuft, symmetrisch sind.

1.5

Schnittstelle für die Parameter $a=1$ und $a=2$

$\begin{array}[t]{rll} f_1(t)& = &f_2(t)\quad \scriptsize\;\\[5pt] \mathrm e^{1 \cdot t-0,3 \cdot t^2}& = &\mathrm e^{2\cdot t-0,3 \cdot t^2}\quad \scriptsize\;\\[5pt] t-0,3 \cdot t^2& = &2t-0,3 \cdot t^2\quad \scriptsize\;\\[5pt] t& = &0\quad \scriptsize\;\\[5pt] \end{array}$

Ermittelte $t$ in eine beliebige Funktion $f_a$ der Schar einsetzten:

$f_a(0)=\mathrm e^{a\cdot 0-0,3\cdot 0^2}=\mathrm e^0=1$

Die Graphen zweier beliebiger Funktionen der Schar $f_a$ haben genau einen gemeinsamen Punkt bei $P(0\mid 1)$ .

Der Schnittpunkt mit der $y$ -Achse jedes Graphen von $f_a$ ist unabhängig von $a,$ da $x=0$ ist und somit haben alle Funktionen der Schar die selben Koordinaten an dieser Stelle.

2.1

Bestimmen einer Stammfunktion und des Schnittpunktes mit der $y-$ Achse mit dem CAS:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

Mit einem passenden $c$ , für welches $F(0)=0$ gilt, folgt:

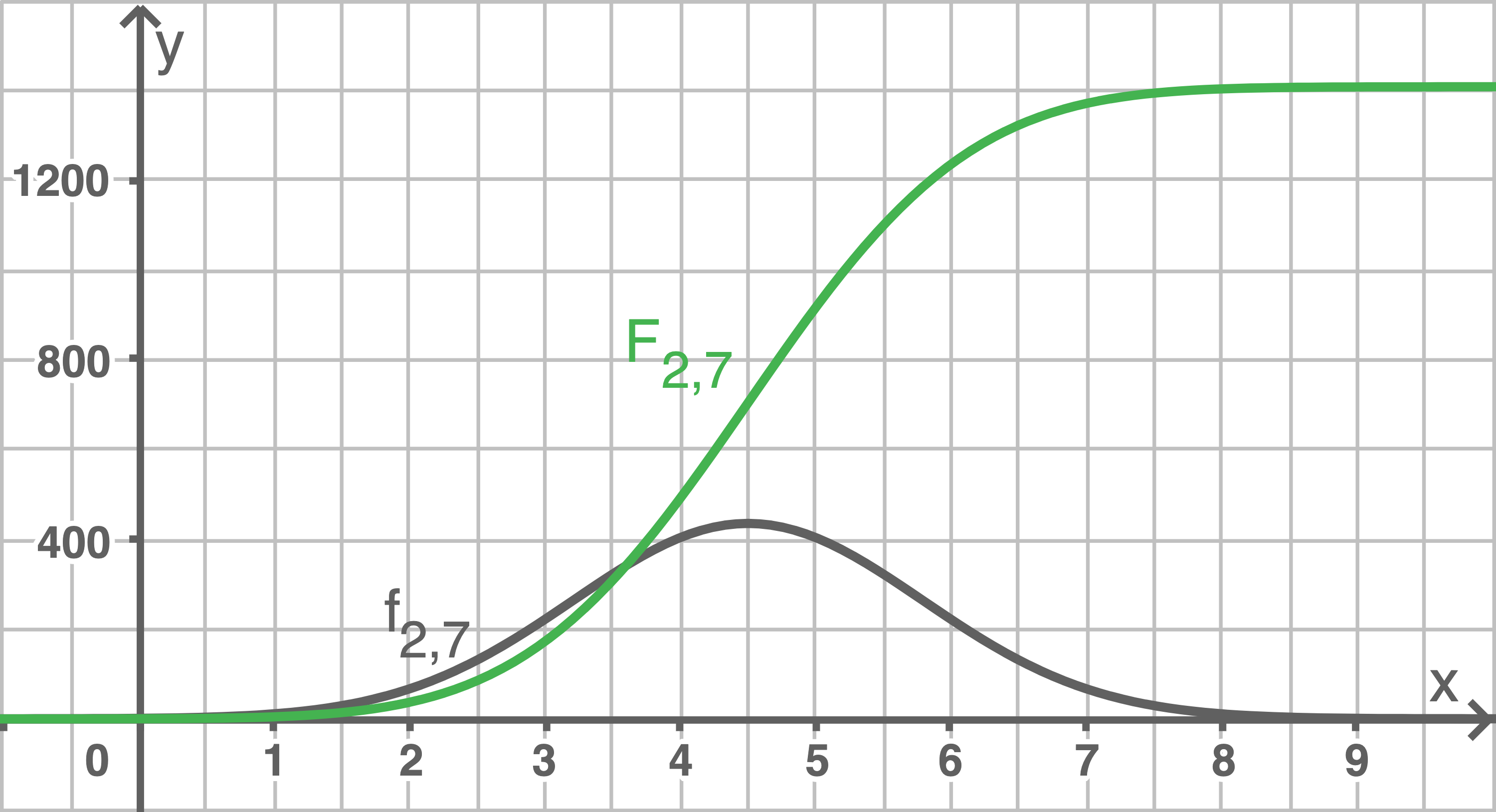
An der Stelle des Hochpunktes des Graphen von $f_{2,7}$ , ist der Graph von $F_{2,7}$ am steilsten und besitzt einen Wendepunkt.

2.2

Sinkt $f_{2,7}$ unter den Wert $0,0005$ ist im Modell davon auszugehen, dass keine Bakterien mehr vorhanden sind.

Mit dem CAS folgt:

$\begin{array}[t]{rll} f_{2,7}(t)=0,0005 &=& \mathrm e^{2,7t-0,3t^2}\\[5pt] t_1\approx 11,25\quad t_2&\approx& -2,25\\[5pt] \end{array}$

Da $t_2$ negativ ist und somit in der Vergangenheit liegt, ist davon auszugehen, dass nach $11$ Tagen und etwa $6$ Stunden keine Bakterien mehr vorhanden sind.

2.3

Mit Hilfe des CAS lässt sich das Maximum der Ableitung von $\(f$ über die notwendige Bedingung $\(f$ bestimmen.

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

$\(f$

$\( f$

Mit dem CAS folgt:

$\begin{array}[t]{rll} \mathrm e^{2,7t-0,3t^2} (-0,6)(2,7-0,6t)^2&=& 0 \\[5pt] t&=& 4,5 \quad \scriptsize\;\\[5pt] \end{array}$

Nachweis des Vorzeichenwechsels:

$\( f$
$\(f$

Nach viereinhalb Tagen ist der Bakterienbestand am größten.

2.4

$\dfrac{f_{2,7}(2)+f_{2,7}(1)}{2}=\dfrac{66,69+11,02}{2}\approx38,86$

Die mittlere Anzahl der Bakterien während des zweiten Tages nach Beobachtungsbeginn beträgt ungefähr $39 000$ Bakterien.

2.5

Beim Anlegen, einer Sekante in einem bestimmten Intervall $[a;b]$ an den Graphen der Funktion, liegt bei einer Linkskrümmung des Graphen die Sekante oberhalb des Graphen, wodurch der Flächeninhalt des Trapezes deutlich höhere Werte, als die genaue Berechnung mithilfe des Integrals, liefert.
Bei einer Rechtskrümmung des Graphen liegt die Sekante unterhalb des Graphen, sodass bei der Berechnung des Flächeninhalts kleinere Werte bestimmt werden.
Beim Krümmungswechsel (Wendestelle) liegt die Sekante allerdings teils unterhalb, teils oberhalb des Graphen, sodass hier ein Intervall der Länge $1$ existiert, in dem der Näherungswert durch die Trapezfläche exakt denselben Wert annimmmt, wie durch die Berechung des Mittelwerts $m$ für das Intervall. Aus Symmetriegründen des Graphen von $f_{2,7},$ der zwei Wendestellen besitzt, gibt es somit genau zwei solche Intervalle, in denen die beschriebene Eigenschaft zutrifft.

2.6

Untersumme über fünf gleich breite Rechtecke $\Rightarrow b=0,2.$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rll} f_{2,7}(1,0)&\approx& 11,02\quad \scriptsize\;\\[5pt] f_{2,7}(1,2)&\approx& 16,58\quad \scriptsize\;\\[5pt] f_{2,7}(1,4)&\approx& 24,34\quad \scriptsize\;\\[5pt] f_{2,7}(1,6)&\approx& 34,88\quad \scriptsize\;\\[5pt] f_{2,7}(1,8)&\approx& 48,81\quad \scriptsize\;\\[5pt] \end{array}$

$\dfrac{f(1,0)+f(1,2)+f(1,4)+f(1,6)+f(1,8)}{5}=27,126$

Die mittlere Anzahl an Bakterien während des zweiten Tages beträgt etwa $27,126$ .

2.7

Der Nährungswert wird genauer, wenn nicht die Untersumme mit den Rechtecken berechnet wird, sondern die Höhe der Rechtecke so angesetzt wird, dass genau die Hälfte des Rechtecks über und unter dem Graphen von $f_{2,7}$ liegt. Ebenso kann die Anzahl der Rechtecke, durch eine Verringerung der Breite, erhöht werden.

3.0

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$\begin{array}[t]{rll} V& = & \pi\cdot\displaystyle\int_{-1}^{1}(0,5\cdot\sqrt{1-x^2})^2\; \mathrm dx\quad \scriptsize\;\\[5pt] & = & 2\pi\cdot\displaystyle\int_{0}^{1}(0,5\cdot\sqrt{1-x^2})^2\; \mathrm dx\quad \scriptsize\;\\[5pt] & = &\dfrac{\pi}{3} \end{array}$

$\dfrac{\pi}{3}\cdot \dfrac{2}{0,01}=209,4$

Die Tablette enthält etwa $209,4\,\text{mg}$ Antibiotikum.