B2 - Analytische Geometrie
1.
Ein Baugrundstück in Hanglage besitzt die Eckpunkte  ,
,  ,
,  und
und  . Modellhaft soll angenommen werden, dass das Grundstück in einer Ebene
. Modellhaft soll angenommen werden, dass das Grundstück in einer Ebene  liegt.
liegt.
(Alle Koordinaten sind in Metern angegeben.)
(Alle Koordinaten sind in Metern angegeben.)
1.1
Gib eine Parameterform der Ebene  an und bestimme eine Koordinatengleichung dieser Ebene.
an und bestimme eine Koordinatengleichung dieser Ebene.
(5 BE)
1.2
Zeige durch Rechnung, dass das Viereck  ein Rechteck ist.
ein Rechteck ist.
(3 BE)
1.3
In der Planungsskizze (Material) erscheint das Viereck  als Viereck
als Viereck  , das durch eine senkrechte Projektion in die
, das durch eine senkrechte Projektion in die  -
- -Ebene entsteht. Dadurch ändern sich u.a. die Seitenlängen des Vierecks. Bestätige dies rechnerisch beispielhaft an den Seiten
-Ebene entsteht. Dadurch ändern sich u.a. die Seitenlängen des Vierecks. Bestätige dies rechnerisch beispielhaft an den Seiten  und
und  .
.
(3 BE)
2.
Mithilfe eines Baggers wird eine Baugrube ausgehoben, sodass die rechteckige Grundfläche des Hauses, das auf dem Grundstück gebaut werden soll, freigelegt wird. Diese liegt in der  -
- -Ebene und besitzt die Eckpunkte
-Ebene und besitzt die Eckpunkte  ,
,  ,
,  und
und  (Material).
(Material).
2.1
Berechne die Koordinaten des Eckpunktes  .
.
(2 BE)
2.2
Berechne den spitzen Winkel, um welchen die Grundfläche des Hauses in der  -
- -Ebene gedreht werden müsste, damit die längere Seite der Grundfläche in der Planungsskizze parallel zur Strecke
-Ebene gedreht werden müsste, damit die längere Seite der Grundfläche in der Planungsskizze parallel zur Strecke  verläuft.
verläuft.
(3 BE)
3.
Lineare Abbildungen in der Ebene wie z.B. Spiegelungen an den Koordinatenachsen oder Drehungen um den Koordinatenursprung lassen sich durch 2x2-Matrizen darstellen. Die Verkettung solcher Abbildungen entspricht dann dem Produkt der jeweiligen Matrizen. Lässt man z.B. einen Punkt  mit dem Drehwinkel
mit dem Drehwinkel  gegen den Uhrzeigersinn um den Koordinatenursprung rotieren, so erhält man als Ergebnis den Bildpunkt
gegen den Uhrzeigersinn um den Koordinatenursprung rotieren, so erhält man als Ergebnis den Bildpunkt  durch folgende Gleichung:
durch folgende Gleichung:
 mit der Rotationsmatrix
mit der Rotationsmatrix 
3.1
Der Punkt  wird mit dem Drehwinkel
wird mit dem Drehwinkel  um den Ursprung gedreht. Berechne die Koordinaten des Bildpunktes
um den Ursprung gedreht. Berechne die Koordinaten des Bildpunktes  mit Hilfe der Rotationsmatrix
mit Hilfe der Rotationsmatrix  und bestätige durch Rechnung, dass eine Drehung von
und bestätige durch Rechnung, dass eine Drehung von  um
um  , also die Verkettung zweier
, also die Verkettung zweier  -Drehungen, durch das Produkt
-Drehungen, durch das Produkt  beschrieben wird.
beschrieben wird.
Da die Verschiebung eines Punktes
(3 BE)
und die 2x2-Matrix
3.2
Wie in Aufgabe 3.1 wird der Punkt  mit dem Drehwinkel
mit dem Drehwinkel  um den Ursprung gedreht. Berechne nun die Koordinaten
um den Ursprung gedreht. Berechne nun die Koordinaten  und
und  des Bildpunktes
des Bildpunktes  unter Verwendung homogener Koordinaten mit Hilfe der entsprechenden Rotationsmatrix.
unter Verwendung homogener Koordinaten mit Hilfe der entsprechenden Rotationsmatrix.
(2 BE)
3.3
Zeige, dass unter Verwendung homogener Koordinaten die Matrix  die Verschiebung eines Punktes
die Verschiebung eines Punktes  zum Punkt
zum Punkt  in der Ebene beschreibt.
in der Ebene beschreibt.
(4 BE)
3.4
Unter Verwendung der  - und der
- und der  -Koordinate des Punktes
-Koordinate des Punktes  erhält man den Punkt
erhält man den Punkt  . Aus dem Ortsvektor des Punktes
. Aus dem Ortsvektor des Punktes  wird bei Verwendung homogener Koordinaten der Vektor
wird bei Verwendung homogener Koordinaten der Vektor  . Erläutere die geometrische Bedeutung folgender Gleichung und der darin enthaltenen Teilausdrücke:
. Erläutere die geometrische Bedeutung folgender Gleichung und der darin enthaltenen Teilausdrücke:





Material
Planungsskizze
(5 BE)
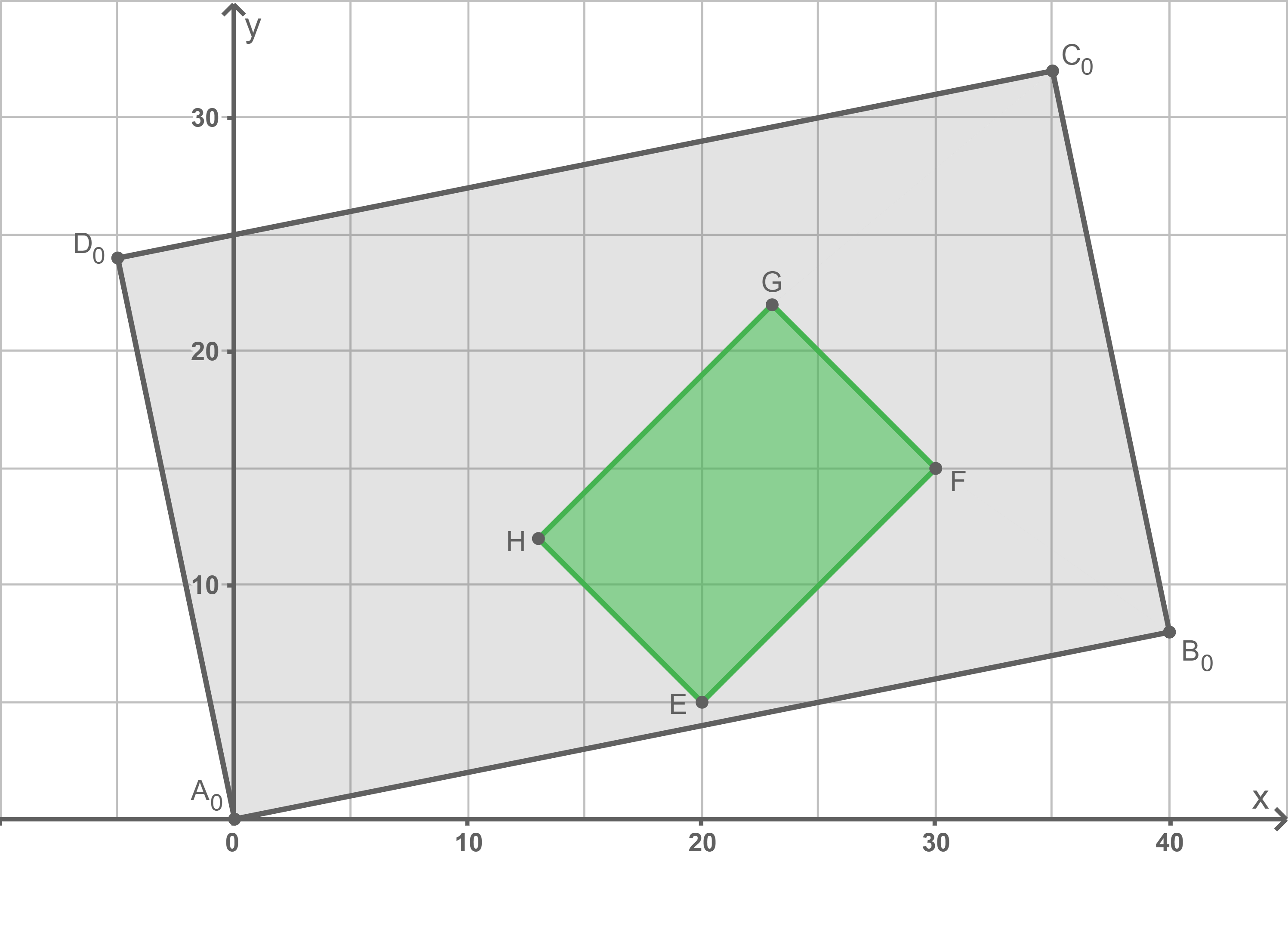
Hinweis:
Die positive -Achse zeigt senkrecht zur
-Achse zeigt senkrecht zur  -
- -Ebene in Richtung des Betrachters.
-Ebene in Richtung des Betrachters.
Die positive
1.1
Ebenengleichung in Parameterform aufstellen
Koordinatengleichung angeben
Normalenvektor berechnen:
 und die Koordinaten des Punktes
und die Koordinaten des Punktes  in die allgemeine Koordinatengleichung einsetzen:
in die allgemeine Koordinatengleichung einsetzen:
![\(\begin{array}[t]{rll}
L:\quad n_1x + n_2y +n_3z &=& d \\[5pt]
-80\cdot 0 -100\cdot 0 + 1.000\cdot (-1)&=& d \\[5pt]
-1.000&=&d
\end{array}\)](https://mathjax.schullv.de/96036bab470b82af4ee3160480034ff5bc082ba736dfd63dabb10dbc363e0d63?color=5a5a5a) Daraus folgt:
Daraus folgt:

1.2
Nachweisen, dass es sich um ein Rechteck handelt
Damit es sich um ein Rechteck müssen folgende Eigenschaften erfüllt sein:
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=&\overrightarrow{DC} &\quad \\[5pt]
\pmatrix{40-0 \\ 8-0 \\ 3-(-1)}&=&\pmatrix{35-(-5) \\ 32-24 \\ 5-1}\\[5pt]
\pmatrix{40 \\ 8 \\ 4}&=&\pmatrix{40 \\ 8 \\ 4}
\end{array}\)](https://mathjax.schullv.de/4f032d68e1310b0851c079763e9b81a0c68022f49a4b79885d48279fe11a215b?color=5a5a5a) 2. Schritt: Zeigen, dass zwei benachbarte Vektoren orthogonal zueinander sind
2. Schritt: Zeigen, dass zwei benachbarte Vektoren orthogonal zueinander sind
 Berechnung des Skalarproduktes
Berechnung des Skalarproduktes 
 mit dem CAS liefert:
mit dem CAS liefert:



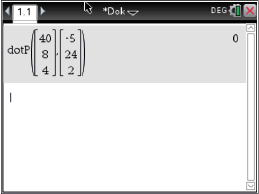 Da das Skalarprodukt Null ist liegen die beiden Vektoren orthogonal zueinander und da auch die gegenüberliegenden Seiten gleich lang sind, muss es sich bei dem Viereck
Da das Skalarprodukt Null ist liegen die beiden Vektoren orthogonal zueinander und da auch die gegenüberliegenden Seiten gleich lang sind, muss es sich bei dem Viereck  um ein Rechteck handeln.
um ein Rechteck handeln.
- Zwei gegenüberliegende Vektoren sind gleich
- Zwei benachbarte Vektoren sind orthogonal zueienander

1.3
Vektorlänge der Vektoren  und
und  berechnen
Da es sich bei dem Vektor
berechnen
Da es sich bei dem Vektor  um eine Projektion des Vektors
um eine Projektion des Vektors  in die
in die  -
- -Ebene handelt, ergibt sich
-Ebene handelt, ergibt sich  aus
aus  so, dass die
so, dass die  -Koordinate des Vektors
-Koordinate des Vektors  gleich Null gesetzt wird. Mit Hilfe des CAS folgt für die Längen der Vektoren:
gleich Null gesetzt wird. Mit Hilfe des CAS folgt für die Längen der Vektoren:




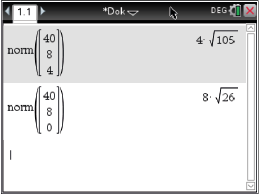 Der Vektor
Der Vektor  hat die Länge
hat die Länge  und der Vektor
und der Vektor  hat die Länge
hat die Länge  , wodurch ersichtlich wird, dass sich durch die senkrechte Projektion die Seitenlängen ändern.
, wodurch ersichtlich wird, dass sich durch die senkrechte Projektion die Seitenlängen ändern.

2.1
Koordinaten des Eckpunktes  berechnen
Hierfür wird zuerst der Vektor
berechnen
Hierfür wird zuerst der Vektor  berechnet und anschließend zu dem Ortsvektor von
berechnet und anschließend zu dem Ortsvektor von  addiert.
addiert.

![\(\begin{array}[t]{rll}
\overrightarrow{OF}&=&\overrightarrow{OE}+\overrightarrow{HG} \\
&=&\pmatrix{20 \\ 5 \\ 0}+\pmatrix{10 \\ 10 \\ 0}=\pmatrix{30 \\ 15 \\ 0}
\end{array}\)](https://mathjax.schullv.de/9313dcb1fbfbb66798c4ee9e9c2c003c9e0228348e989f1003d7ecfc50d74003?color=5a5a5a) Somit lauten die Koordinaten des Punktes
Somit lauten die Koordinaten des Punktes  .
.
2.2
Winkel zwischen den Vektoren  und
und berechnen
Für die weiteren Berechnungen heißt der Winkel
berechnen
Für die weiteren Berechnungen heißt der Winkel  .
.
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\overrightarrow{EF} \cdot \overrightarrow{A_0B_0}}{|\overrightarrow{EF}\cdot|\overrightarrow{A_0B_0}|} \\[5pt]
&=&\dfrac{\pmatrix{10 \\ 10 \\ 0}\cdot \pmatrix{40 \\ 8 \\ 0}}{\left\vert\pmatrix{10 \\ 10 \\ 0}\right\vert\cdot\left\vert\pmatrix{40 \\ 8 \\ 0}\right\vert}
\\[5pt]
&=&\dfrac{10\cdot40+10\cdot8+0\cdot0}{\sqrt{200}\cdot\sqrt{1664}}\\[5pt]
&=&\dfrac{480}{\sqrt{200}\cdot\sqrt{1664}}\\[5pt]
&=& 0,83\\[5pt]
\alpha&=& \cos^{-1}(0,83) = 33,9^{\circ}
\end{array}\)](https://mathjax.schullv.de/762a5daff1377f44918db26461b27d2d0946f526af93973aec2725c57cc29221?color=5a5a5a) Das bedeutet, dass die Grundfläche des Hauses um
Das bedeutet, dass die Grundfläche des Hauses um  gedreht werden muss.
gedreht werden muss.
3.1
Koordinaten Bildpunktes  berechnen
Die Berechnung von
berechnen
Die Berechnung von 
 mit Hilfe des CAS liefert für den Punkt
mit Hilfe des CAS liefert für den Punkt 


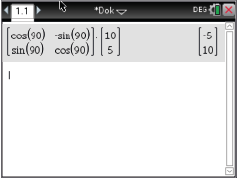 Somit lauten die Koordinaten des Punktes
Somit lauten die Koordinaten des Punktes  .
Bestätigen, dass eine Drehung von
.
Bestätigen, dass eine Drehung von  um 180
um 180 durch das Produkt
durch das Produkt  beschrieben wird:
beschrieben wird:

3.2
Koordinaten des Bildpunktes  berechnen unter Verwendung homogener Koordinaten
Daraus folgt:
berechnen unter Verwendung homogener Koordinaten
Daraus folgt: 
3.3
Koordinaten des neuen Punktes  mit homogener Koordinaten berechnen
mit homogener Koordinaten berechnen
![\(\begin{array}[t]{rll}
\pmatrix{x‘ \\ y‘ \\ 1}&=& T \cdot \pmatrix{x \\ y \\ 1} \\[5pt]
&=& \begin{pmatrix} 1 & 0 & s \\ 0 & 1 & t \\ 0 & 0 & 1 \end{pmatrix} \cdot \pmatrix{x \\ y \\ 1} \\[5pt]
&=& \pmatrix{1\cdot x+0\cdot y+s\cdot1 \\ 0\cdot x+1\cdot y+t\cdot1 \\ 0\cdot x+0\cdot y+1\cdot1}\\[5pt]
&=& \pmatrix{x+s \\ y+t \\ 1}
\end{array}\)](https://mathjax.schullv.de/18c00aa566c47bfc5d81dbdf929149baa2718124e75dc765c084124a9f878c79?color=5a5a5a) Da die
Da die  -Koordinate 1 bleibt, und die
-Koordinate 1 bleibt, und die  und
und  Koordinaten zu den aus der Aufgabenstellung übereinstimmen, handelt es sich um die Verschiebung in der Ebene.
Koordinaten zu den aus der Aufgabenstellung übereinstimmen, handelt es sich um die Verschiebung in der Ebene.
3.4
Gleichung erläutern
Teil  der Gleichung beschreibt eine Verschiebung des Punktes
der Gleichung beschreibt eine Verschiebung des Punktes  um 13 Einheiten in
um 13 Einheiten in  -Richtung und um 12 Einheiten in
-Richtung und um 12 Einheiten in  -Richtung, da es sich hierbei um die Matrix
-Richtung, da es sich hierbei um die Matrix  handelt mit
handelt mit  und
und  Teil
Teil  beschreibt die Drehung eines Punktes um 45
beschreibt die Drehung eines Punktes um 45 , da
, da  ist.
Teil
ist.
Teil  bewirkt eine Verschiebung um -13 Einheiten in
bewirkt eine Verschiebung um -13 Einheiten in  -Richtung und -12 Einheiten in
-Richtung und -12 Einheiten in  -Richtung.
Teil
-Richtung.
Teil  ist der Ortsvektor des Punktes
ist der Ortsvektor des Punktes  , auf welchen die Verschiebungen und Rotationen angewendet werden.
Zusammenfassend wird der Punkt
, auf welchen die Verschiebungen und Rotationen angewendet werden.
Zusammenfassend wird der Punkt  insgesamt um
insgesamt um  in der
in der  -
- -Ebene gegen den Uhrzeigersinn um den Rotationsmittelpunkt
-Ebene gegen den Uhrzeigersinn um den Rotationsmittelpunkt  gedreht.
gedreht.
1.1
Ebenengleichung in Parameterform aufstellen
Koordinatengleichung angeben
Normalenvektor berechnen:
 und die Koordinaten des Punktes
und die Koordinaten des Punktes  in die allgemeine Koordinatengleichung einsetzen:
in die allgemeine Koordinatengleichung einsetzen:
![\(\begin{array}[t]{rll}
L:\quad n_1x + n_2y +n_3z &=& d \\[5pt]
-80\cdot 0 -100\cdot 0 + 1.000\cdot (-1)&=& d \\[5pt]
-1.000&=&d
\end{array}\)](https://mathjax.schullv.de/96036bab470b82af4ee3160480034ff5bc082ba736dfd63dabb10dbc363e0d63?color=5a5a5a) Daraus folgt:
Daraus folgt:

1.2
Nachweisen, dass es sich um ein Rechteck handelt
Damit es sich um ein Rechteck müssen folgende Eigenschaften erfüllt sein:
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=&\overrightarrow{DC} &\quad \\[5pt]
\pmatrix{40-0 \\ 8-0 \\ 3-(-1)}&=&\pmatrix{35-(-5) \\ 32-24 \\ 5-1}\\[5pt]
\pmatrix{40 \\ 8 \\ 4}&=&\pmatrix{40 \\ 8 \\ 4}
\end{array}\)](https://mathjax.schullv.de/4f032d68e1310b0851c079763e9b81a0c68022f49a4b79885d48279fe11a215b?color=5a5a5a) 2. Schritt: Zeigen, dass zwei benachbarte Vektoren orthogonal zueinander sind
2. Schritt: Zeigen, dass zwei benachbarte Vektoren orthogonal zueinander sind
 Berechnung des Skalarproduktes
Berechnung des Skalarproduktes 
 mit dem CAS liefert:
mit dem CAS liefert:



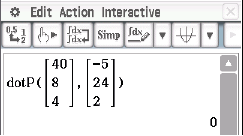 Da das Skalarprodukt Null ist liegen die beiden Vektoren orthogonal zueinander und da auch die gegenüberliegenden Seiten gleich lang sind, muss es sich bei dem Viereck
Da das Skalarprodukt Null ist liegen die beiden Vektoren orthogonal zueinander und da auch die gegenüberliegenden Seiten gleich lang sind, muss es sich bei dem Viereck  um ein Rechteck handeln.
um ein Rechteck handeln.
- Zwei gegenüberliegende Vektoren sind gleich
- Zwei benachbarte Vektoren sind orthogonal zueienander

1.3
Vektorlänge der Vektoren  und
und  berechnen
Da es sich bei dem Vektor
berechnen
Da es sich bei dem Vektor  um eine Projektion des Vektors
um eine Projektion des Vektors  in die
in die  -
- -Ebene handelt, ergibt sich
-Ebene handelt, ergibt sich  aus
aus  so, dass die
so, dass die  -Koordinate des Vektors
-Koordinate des Vektors  gleich Null gesetzt wird. Mit Hilfe des CAS folgt für die Längen der Vektoren:
gleich Null gesetzt wird. Mit Hilfe des CAS folgt für die Längen der Vektoren:




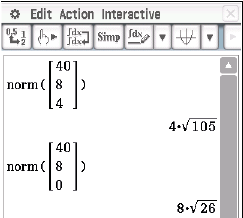 Der Vektor
Der Vektor  hat die Länge
hat die Länge  und der Vektor
und der Vektor  hat die Länge
hat die Länge  , wodurch ersichtlich wird, dass sich durch die senkrechte Projektion die Seitenlängen ändern.
, wodurch ersichtlich wird, dass sich durch die senkrechte Projektion die Seitenlängen ändern.

2.1
Koordinaten des Eckpunktes  berechnen
Hierfür wird zuerst der Vektor
berechnen
Hierfür wird zuerst der Vektor  berechnet und anschließend zu dem Ortsvektor von
berechnet und anschließend zu dem Ortsvektor von  addiert.
addiert.

![\(\begin{array}[t]{rll}
\overrightarrow{OF}&=&\overrightarrow{OE}+\overrightarrow{HG} \\
&=&\pmatrix{20 \\ 5 \\ 0}+\pmatrix{10 \\ 10 \\ 0}=\pmatrix{30 \\ 15 \\ 0}
\end{array}\)](https://mathjax.schullv.de/9313dcb1fbfbb66798c4ee9e9c2c003c9e0228348e989f1003d7ecfc50d74003?color=5a5a5a) Somit lauten die Koordinaten des Punktes
Somit lauten die Koordinaten des Punktes  .
.
2.2
Winkel zwischen den Vektoren  und
und berechnen
Für die weiteren Berechnungen heißt der Winkel
berechnen
Für die weiteren Berechnungen heißt der Winkel  .
.
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\overrightarrow{EF} \cdot \overrightarrow{A_0B_0}}{|\overrightarrow{EF}\cdot|\overrightarrow{A_0B_0}|} \\[5pt]
&=&\dfrac{\pmatrix{10 \\ 10 \\ 0}\cdot \pmatrix{40 \\ 8 \\ 0}}{\left\vert\pmatrix{10 \\ 10 \\ 0}\right\vert\cdot\left\vert\pmatrix{40 \\ 8 \\ 0}\right\vert}
\\[5pt]
&=&\dfrac{10\cdot40+10\cdot8+0\cdot0}{\sqrt{200}\cdot\sqrt{1664}}\\[5pt]
&=&\dfrac{480}{\sqrt{200}\cdot\sqrt{1664}}\\[5pt]
&=& 0,83\\[5pt]
\alpha&=& \cos^{-1}(0,83) = 33,9^{\circ}
\end{array}\)](https://mathjax.schullv.de/762a5daff1377f44918db26461b27d2d0946f526af93973aec2725c57cc29221?color=5a5a5a) Das bedeutet, dass die Grundfläche des Hauses um
Das bedeutet, dass die Grundfläche des Hauses um  gedreht werden muss.
gedreht werden muss.
3.1
Koordinaten Bildpunktes  berechnen
Die Berechnung von
berechnen
Die Berechnung von 
 mit Hilfe des CAS liefert für den Punkt
mit Hilfe des CAS liefert für den Punkt 


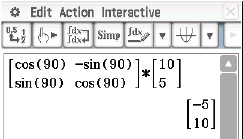 Somit lauten die Koordinaten des Punktes
Somit lauten die Koordinaten des Punktes  .
Bestätigen, dass eine Drehung von
.
Bestätigen, dass eine Drehung von  um 180
um 180 durch das Produkt
durch das Produkt  beschrieben wird:
beschrieben wird:

3.2
Koordinaten des Bildpunktes  berechnen unter Verwendung homogener Koordinaten
Daraus folgt:
berechnen unter Verwendung homogener Koordinaten
Daraus folgt: 
3.3
Koordinaten des neuen Punktes  mit homogener Koordinaten berechnen
mit homogener Koordinaten berechnen
![\(\begin{array}[t]{rll}
\pmatrix{x‘ \\ y‘ \\ 1}&=& T \cdot \pmatrix{x \\ y \\ 1} \\[5pt]
&=& \begin{pmatrix} 1 & 0 & s \\ 0 & 1 & t \\ 0 & 0 & 1 \end{pmatrix} \cdot \pmatrix{x \\ y \\ 1} \\[5pt]
&=& \pmatrix{1\cdot x+0\cdot y+s\cdot1 \\ 0\cdot x+1\cdot y+t\cdot1 \\ 0\cdot x+0\cdot y+1\cdot1}\\[5pt]
&=& \pmatrix{x+s \\ y+t \\ 1}
\end{array}\)](https://mathjax.schullv.de/18c00aa566c47bfc5d81dbdf929149baa2718124e75dc765c084124a9f878c79?color=5a5a5a) Da die
Da die  -Koordinate 1 bleibt, und die
-Koordinate 1 bleibt, und die  und
und  Koordinaten zu den aus der Aufgabenstellung übereinstimmen, handelt es sich um die Verschiebung in der Ebene.
Koordinaten zu den aus der Aufgabenstellung übereinstimmen, handelt es sich um die Verschiebung in der Ebene.
3.4
Gleichung erläutern
Teil  der Gleichung beschreibt eine Verschiebung des Punktes
der Gleichung beschreibt eine Verschiebung des Punktes  um 13 Einheiten in
um 13 Einheiten in  -Richtung und um 12 Einheiten in
-Richtung und um 12 Einheiten in  -Richtung, da es sich hierbei um die Matrix
-Richtung, da es sich hierbei um die Matrix  handelt mit
handelt mit  und
und  Teil
Teil  beschreibt die Drehung eines Punktes um 45
beschreibt die Drehung eines Punktes um 45 , da
, da  ist.
Teil
ist.
Teil  bewirkt eine Verschiebung um -13 Einheiten in
bewirkt eine Verschiebung um -13 Einheiten in  -Richtung und -12 Einheiten in
-Richtung und -12 Einheiten in  -Richtung.
Teil
-Richtung.
Teil  ist der Ortsvektor des Punktes
ist der Ortsvektor des Punktes  , auf welchen die Verschiebungen und Rotationen angewendet werden.
Zusammenfassend wird der Punkt
, auf welchen die Verschiebungen und Rotationen angewendet werden.
Zusammenfassend wird der Punkt  insgesamt um
insgesamt um  in der
in der  -
- -Ebene gegen den Uhrzeigersinn um den Rotationsmittelpunkt
-Ebene gegen den Uhrzeigersinn um den Rotationsmittelpunkt  gedreht.
gedreht.