B1 - Analytische Geometrie
Drei Punkte  ,
,  und
und  bewegen sich jeweils entlang einer Geraden:
bewegen sich jeweils entlang einer Geraden:
 auf der Geraden
auf der Geraden 
 auf der Geraden
auf der Geraden 
 auf der Geraden
auf der Geraden  Die Punkte
Die Punkte  ,
,  und
und  bilden für alle
bilden für alle  ein Dreieck
ein Dreieck 
1.1
Zeichne in das Koordinatensystem die drei Geraden sowie die Dreiecke  ,
,  und
und  ein.
ein.
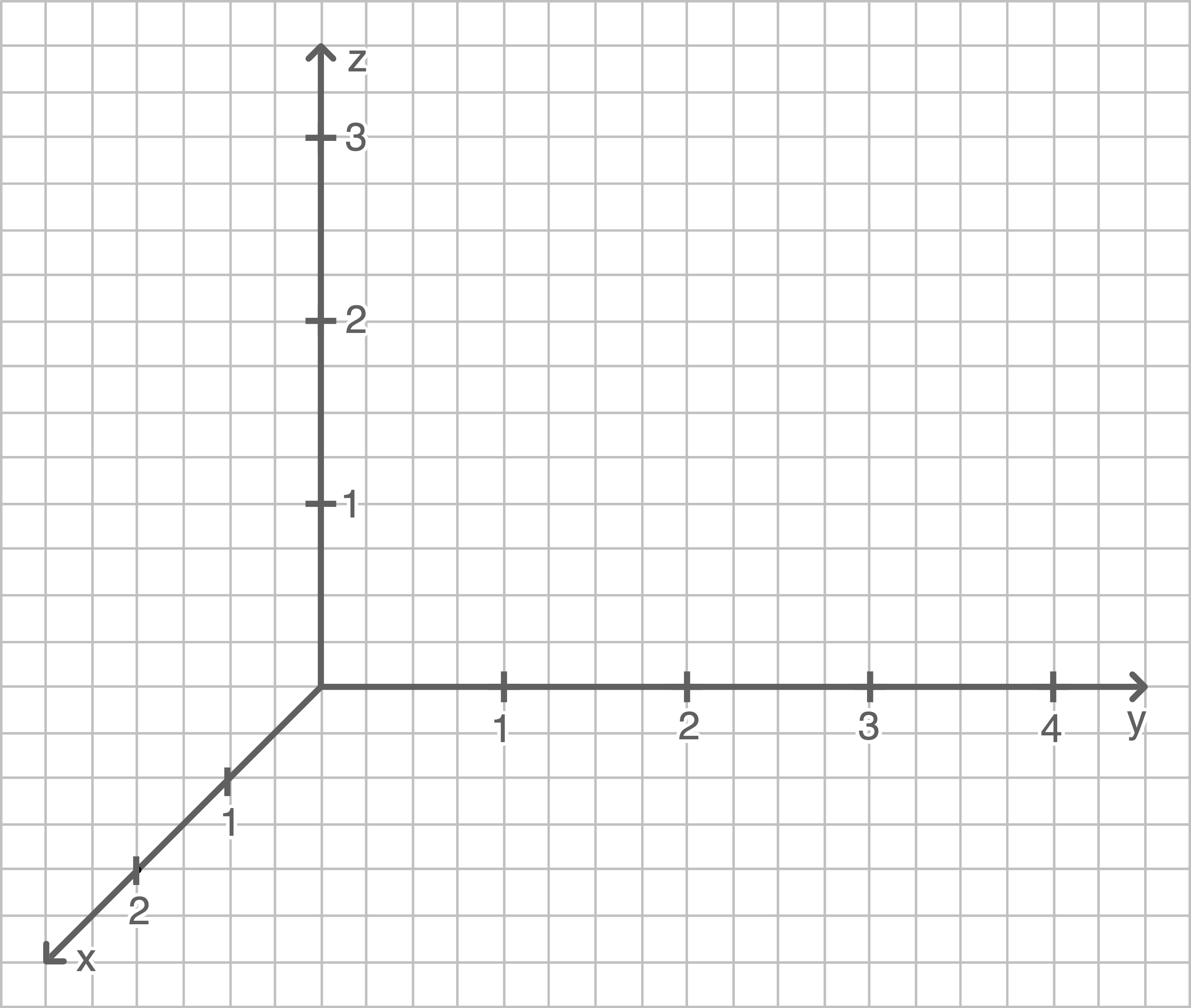

(4 BE)
1.2
Untersuche, ob die Dreiecke  gleichseitig sind.
gleichseitig sind.
(3 BE)
1.3
Die Punkte  ,
,  und
und  legen für jedes
legen für jedes  eine Ebene
eine Ebene  fest.
Bestimme eine Ebenengleichung
fest.
Bestimme eine Ebenengleichung  in Parameterform.
Zeige, dass alle diese Ebenen parallel zueinander sind, und bestimme den Abstand zweier beliebiger dieser Ebenen
in Parameterform.
Zeige, dass alle diese Ebenen parallel zueinander sind, und bestimme den Abstand zweier beliebiger dieser Ebenen  und
und  mit
mit 
(11 BE)
1.4
Berechne den Flächeninhalt des Dreiecks  und untersuche, ob es einen minimalen Flächeninhalt gibt.
und untersuche, ob es einen minimalen Flächeninhalt gibt.
(4 BE)
2
Es sei  der Winkel zwischen den Vektoren
der Winkel zwischen den Vektoren  und
und  Bestätige, dass
Bestätige, dass  gilt.
Beschreibe mit Hilfe des Graphen der Funktion
gilt.
Beschreibe mit Hilfe des Graphen der Funktion  sowie der in Aufgabe 1.3 untersuchten Eigenschaften die Bewegung der Dreiecke.
Untersuche in diesem Zusammenhang auch das Verhalten für betragsmäßig große
sowie der in Aufgabe 1.3 untersuchten Eigenschaften die Bewegung der Dreiecke.
Untersuche in diesem Zusammenhang auch das Verhalten für betragsmäßig große  -Werte.
-Werte.
(8 BE)
1.1
1. Schritt: Geraden einzeichnen
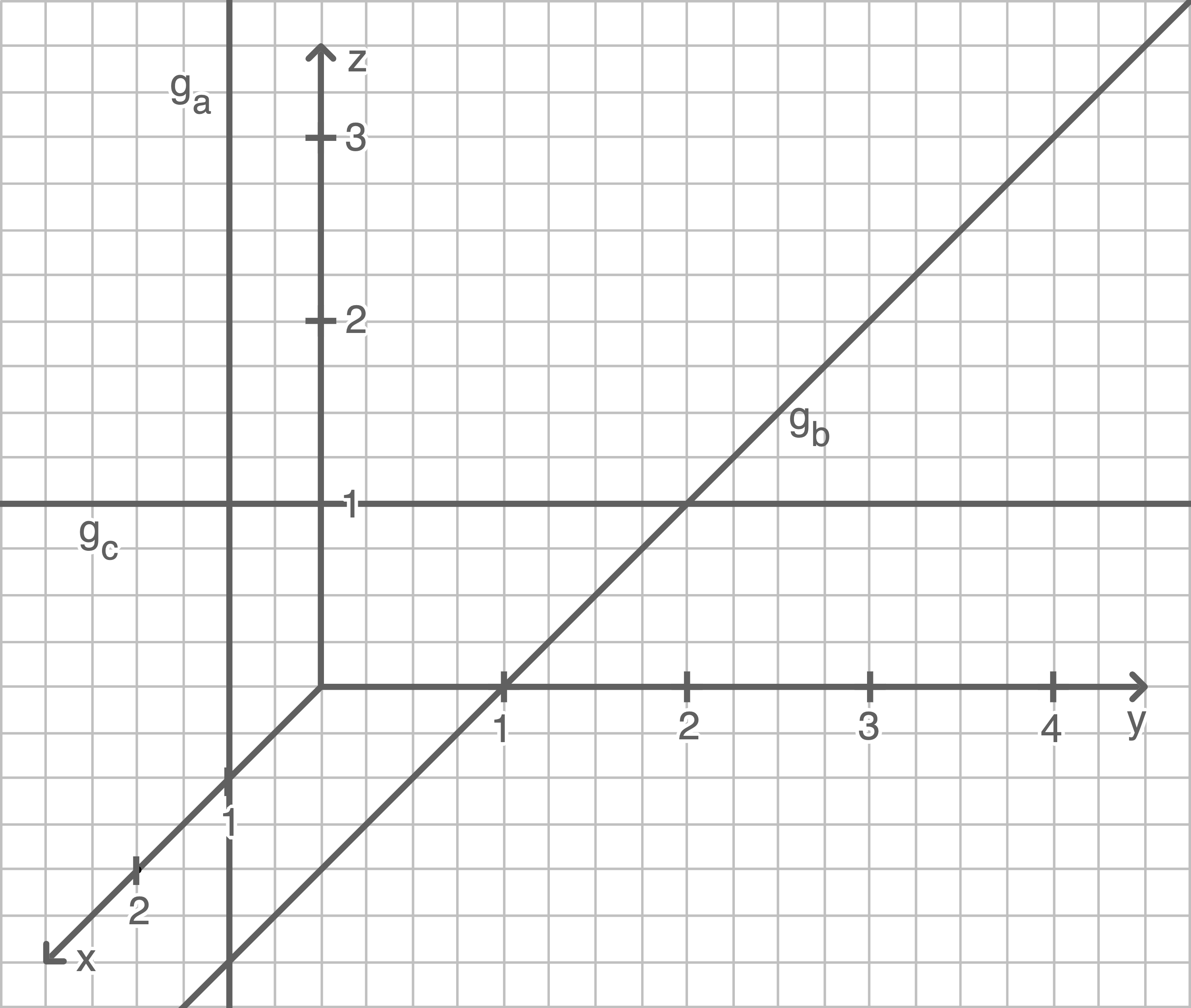 2. Schritt: Dreiecke einzeichnen
Jede Gerade lässt sich als allgemeiner Punkt darstellen:
2. Schritt: Dreiecke einzeichnen
Jede Gerade lässt sich als allgemeiner Punkt darstellen:
 ,
,  ,
,  Für
Für  ,
,  ,
,  folgen somit die Punkte:
folgen somit die Punkte:
 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
,  Eintragen in das Koordinatensystem liefert nun:
Eintragen in das Koordinatensystem liefert nun:
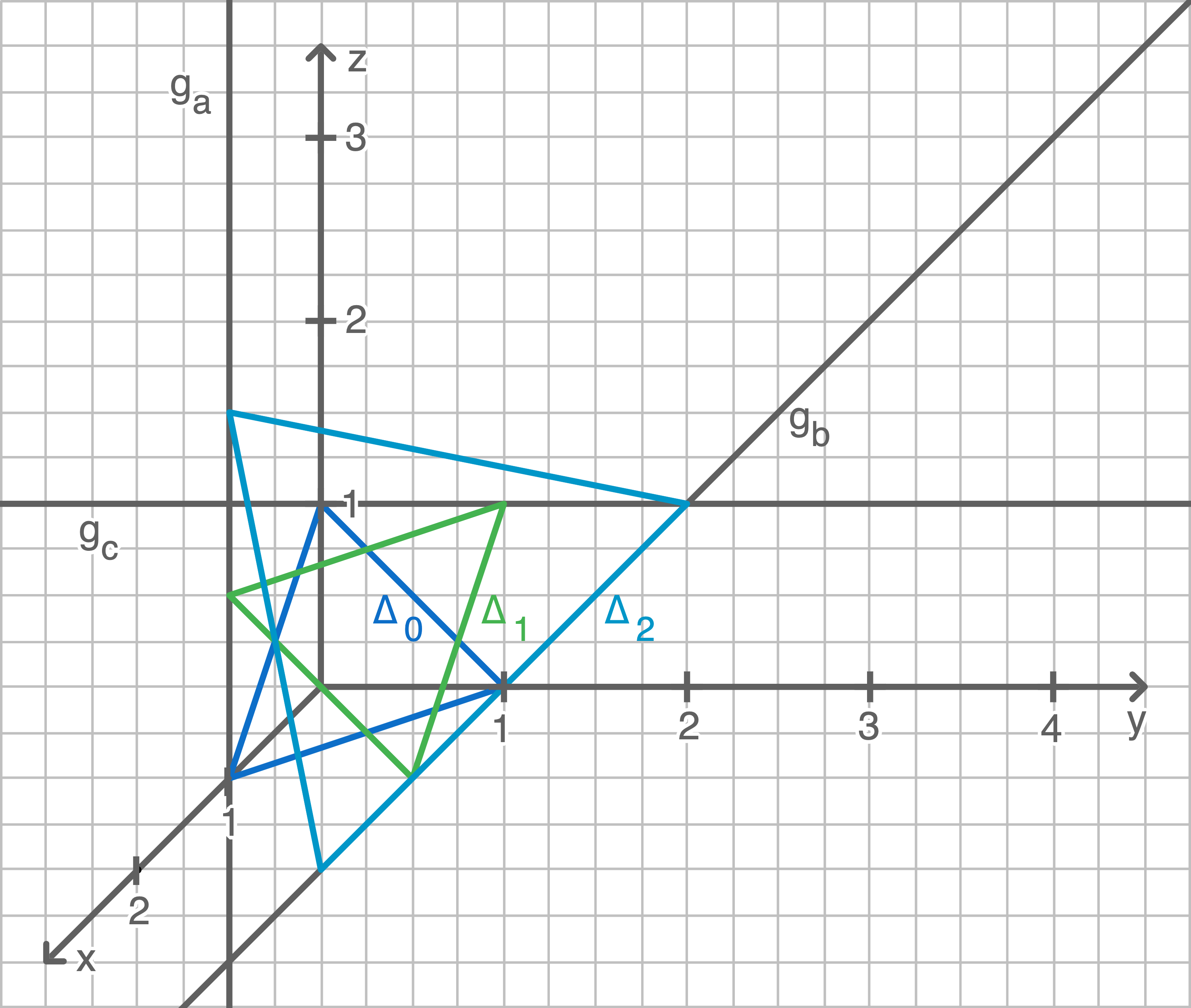


1.2
Ein Dreieck ist genau dann gleichseitig, wenn alle drei Seiten genau gleich lang sind.
![\(\begin{array}[t]{rll}
\,\bigg \vert \,\overrightarrow{A_tB_t}\,\bigg \vert \, &=& \left| \pmatrix{t-1\\1-0\\0-t} \right|& \\[5pt]
&=& \sqrt{(t-1)^2+1^2+(-t)^2}& \\[5pt]
&=&\sqrt{t^2-2t+1+1+t^2}
\end{array}\)](https://mathjax.schullv.de/7c312dc4406bc60f1655b83f4526836f6c5b6166a7faac0e87e6167fcc5b9a54?color=5a5a5a)
![\(\begin{array}[t]{rll}
\,\bigg \vert \,\overrightarrow{A_tC_t}\,\bigg \vert \, &=& \left| \pmatrix{0-1\\t-0\\1-t} \right|& \\[5pt]
&=& \sqrt{(-1)^2+t^2+(1-t)^2}& \\[5pt]
&=&\sqrt{1+t^2+t^2-2t+1}
\end{array}\)](https://mathjax.schullv.de/26157630221ba7c257bd76fde50fba7c6001420090031f716891e4e283339c86?color=5a5a5a)
![\(\begin{array}[t]{rll}
\,\bigg \vert \,\overrightarrow{B_tC_t}\,\bigg \vert \, &=& \left|\pmatrix{0-t\\t-1\\1-0} \right|& \\[5pt]
&=& \sqrt{(-t)^2+(t-1)^2+1^2}& \\[5pt]
&=& \sqrt{t^2+t^2-2t+1+1}
\end{array}\)](https://mathjax.schullv.de/fbccc82f3a3b0c803dd52fef476ddf73c65115c269f8c1e0c0ab4c697828c2c9?color=5a5a5a) Wegen
Wegen  gilt, dass die Dreiecke
gilt, dass die Dreiecke  folglich gleichseitig sind.
folglich gleichseitig sind.
1.3
Ebenengleichung aufstellen
Ein Stützvektor der Ebene ist beispielsweise gegeben durch  Zwei Richtungsvektoren der Ebene
Zwei Richtungsvektoren der Ebene  sind
sind  und
und  Eine Ebenengleichung von
Eine Ebenengleichung von  in Parameterform folgt somit beispielsweise mit:
Parallelität nachweisen
in Parameterform folgt somit beispielsweise mit:
Parallelität nachweisen
 Mit dem Befehl
Mit dem Befehl  des CAS kann das Vektorprodukt der beiden Richtungsvektoren berechnet werden.
des CAS kann das Vektorprodukt der beiden Richtungsvektoren berechnet werden.
 Ein Normalenvektor folgt also mit:
Ein Normalenvektor folgt also mit:
 Die Normalenvektoren
Die Normalenvektoren  sind für alle Werte von
sind für alle Werte von  Vielfache voneinander. Folglich sind alle Ebenen
Vielfache voneinander. Folglich sind alle Ebenen  parallel zueinander.
Abstand berechnen
Koordinatenform von
parallel zueinander.
Abstand berechnen
Koordinatenform von  aufstellen:
Einsetzen der Koordinaten von
aufstellen:
Einsetzen der Koordinaten von  liefert:
liefert:
![\(\begin{array}[t]{rll}
E_t: (t^2-t+1)\cdot (1+0+t)&=& d & \\[5pt]
t^2-t+1+ (t^2-t+1)\cdot t&=& d & \\[5pt]
t^3+1&=& d
\end{array}\)](https://mathjax.schullv.de/a3163dcff9d5b82571804132a97981e07e86aa74e67df1987eb0b35b8b6e7796?color=5a5a5a) Die Hesse'sche Normalform ergibt sich zu:
Ein Stützvektors von
Die Hesse'sche Normalform ergibt sich zu:
Ein Stützvektors von  ist beispielsweise
ist beispielsweise  Es folgt also:
Der Abstand zwischen zwei Ebenen
Es folgt also:
Der Abstand zwischen zwei Ebenen  und
und  beträgt somit
beträgt somit  Längeneinheiten.
Längeneinheiten.

1.4
Flächeninhalt bestimmen
Der Betrag des Kreuzprodukts zweier Vektoren entspricht dem Flächeninhalt des von den Vektoren aufgespannten Parallelogramms. Da es sich um ein Dreieck handelt, muss dieser halbiert werden.
Mit den Vektoren  und
und  sowie deren Kreuzprodukt aus Aufgabe 1.3 ergibt sich die Funktion
sowie deren Kreuzprodukt aus Aufgabe 1.3 ergibt sich die Funktion  die den Flächeninhalt des Dreiecks in Abhängigkeit von
die den Flächeninhalt des Dreiecks in Abhängigkeit von  beschreibt.
Minimalen Flächeninhalt untersuchen
Notwendige Bedingung für Extremstellen anwenden:
beschreibt.
Minimalen Flächeninhalt untersuchen
Notwendige Bedingung für Extremstellen anwenden:
 Hinreichende Bedingung für Extremstellen anwenden:
Hinreichende Bedingung für Extremstellen anwenden:
 Das Dreieck
Das Dreieck  besitzt somit für
besitzt somit für  einen minimalen Flächeninhalt.
einen minimalen Flächeninhalt.
Mit dem CAS kann die erste Ableitung  der Funktion
der Funktion  bestimmt werden.
Mit dem
bestimmt werden.
Mit dem  -Befehl folgt nun:
-Befehl folgt nun:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/49bd74442e24948e9744a756300fc5f0377e1004e5c06c648172cf3efd13f395?color=5a5a5a)

Erneutes Ableiten von  liefert die zweite Ableitung
liefert die zweite Ableitung  Es gilt:
Es gilt:


2
Gleichung bestätigen
Es gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{u_0}&=& \overrightarrow{b_0}-\overrightarrow{a_0}&\\[5pt]
&=& \pmatrix{0\\1\\0}-\pmatrix{1\\0\\0}&\\[5pt]
&=& \pmatrix{-1\\1\\0}
\end{array}\)](https://mathjax.schullv.de/f2ffebba78c5ecc3d6c2ae0cf04d4baef762fe510f7eb664ad0ade6ba738a06e?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{u_t}&=&\overrightarrow{b_t}-\overrightarrow{a_t} &\\[5pt]
&=& \pmatrix{t\\1\\0}-\pmatrix{1\\0\\t}&\\[5pt]
&=& \pmatrix{t-1\\1\\-t}
\end{array}\)](https://mathjax.schullv.de/69ec6497e8261b807967f6c6e0c84b74d6c7a29dd9e3f184475b8bc217ecf3a5?color=5a5a5a) Somit folgt:
Somit ist die Behauptung aus der Aufgabenstellung gezeigt.
Bewegung beschreiben
Mit dem
Somit folgt:
Somit ist die Behauptung aus der Aufgabenstellung gezeigt.
Bewegung beschreiben
Mit dem  -Modus des CAS kann der Graph der Funktion
-Modus des CAS kann der Graph der Funktion  gezeichnet werden.
gezeichnet werden.
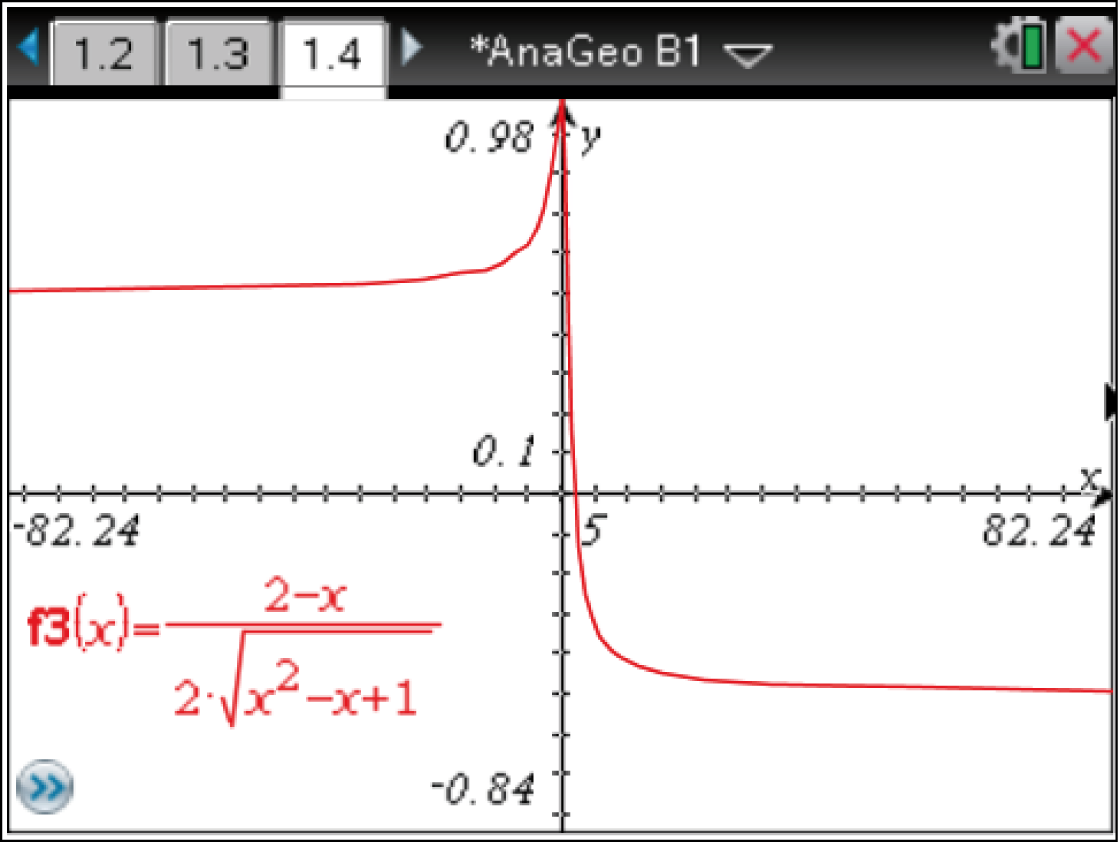
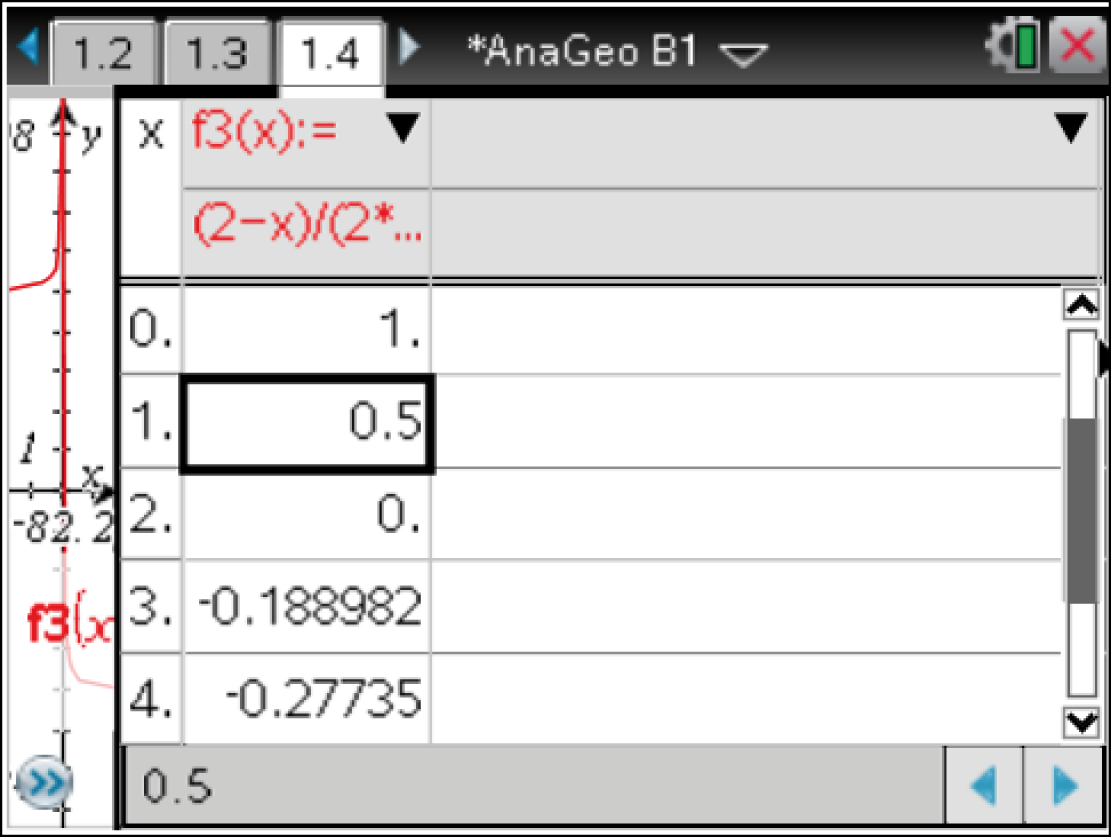 Für betragsmäßig große negative
Für betragsmäßig große negative  -Werte gilt:
-Werte gilt:
![\(\begin{array}[t]{rll}
\cos (\varphi(t))&\approx& 0,5 &\quad \scriptsize \mid\; \cos^{-1}\\[5pt]
\varphi(t)&\approx& 60^\circ
\end{array}\)](https://mathjax.schullv.de/216f65c5f6df8a586e3bf283a544c2d56f3f504896a5d57558b32a9879650c7c?color=5a5a5a) Für betragsmäßig große positive
Für betragsmäßig große positive  -Werte gilt:
-Werte gilt:
![\(\begin{array}[t]{rll}
\cos (\varphi(t))&\approx& -0,5 &\quad \scriptsize \mid\; \cos^{-1}\\[5pt]
\varphi(t)&\approx& 120^\circ
\end{array}\)](https://mathjax.schullv.de/1b8f5ad9aa4b1c3f266188dee335b98e782167e23626ec8f0f57ddcf7a5e4f90?color=5a5a5a) Hinweis: Hierbei muss beachtet werden, dass nicht
Hinweis: Hierbei muss beachtet werden, dass nicht  sondern
sondern  eingestellt ist, da der Winkel berechnet wird.
Für größer werdende negative
eingestellt ist, da der Winkel berechnet wird.
Für größer werdende negative  -Werte nähert sich der Rotationswinkel folglich
-Werte nähert sich der Rotationswinkel folglich  und für größer werdende positive
und für größer werdende positive  -Werte
-Werte  an.
Dem Schaubild aus Aufgabe 1.2 kann entnommen werden, dass die Dreiecke im Uhrzeigersinn rotieren. Beispielsweise ist der Vektor
an.
Dem Schaubild aus Aufgabe 1.2 kann entnommen werden, dass die Dreiecke im Uhrzeigersinn rotieren. Beispielsweise ist der Vektor  im Vergleich zum Vektor
im Vergleich zum Vektor  nach rechts gedreht.
Aus Aufgabe 1.3 folgt:
nach rechts gedreht.
Aus Aufgabe 1.3 folgt:
 im Uhrzeigersinn um den Vektor
im Uhrzeigersinn um den Vektor  sind parallel zueinander und der Abstand zwischen den Dreiecken wird für größer werdende
sind parallel zueinander und der Abstand zwischen den Dreiecken wird für größer werdende  ebenfalls immer größer.
ebenfalls immer größer.


- Die Dreiecke
sind alle parallel zueinander.
- Der Abstand zwischen den Dreiecken wird immer größer:
1.1
1. Schritt: Geraden einzeichnen
 2. Schritt: Dreiecke einzeichnen
Jede Gerade lässt sich als allgemeiner Punkt darstellen:
2. Schritt: Dreiecke einzeichnen
Jede Gerade lässt sich als allgemeiner Punkt darstellen:
 ,
,  ,
,  Für
Für  ,
,  ,
,  folgen somit die Punkte:
folgen somit die Punkte:
 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
,  Eintragen in das Koordinatensystem liefert nun:
Eintragen in das Koordinatensystem liefert nun:



1.2
Ein Dreieck ist genau dann gleichseitig, wenn alle drei Seiten genau gleich lang sind.
![\(\begin{array}[t]{rll}
\,\bigg \vert \,\overrightarrow{A_tB_t}\,\bigg \vert \, &=& \left| \pmatrix{t-1\\1-0\\0-t} \right|& \\[5pt]
&=& \sqrt{(t-1)^2+1^2+(-t)^2}& \\[5pt]
&=&\sqrt{t^2-2t+1+1+t^2}
\end{array}\)](https://mathjax.schullv.de/7c312dc4406bc60f1655b83f4526836f6c5b6166a7faac0e87e6167fcc5b9a54?color=5a5a5a)
![\(\begin{array}[t]{rll}
\,\bigg \vert \,\overrightarrow{A_tC_t}\,\bigg \vert \, &=& \left| \pmatrix{0-1\\t-0\\1-t} \right|& \\[5pt]
&=& \sqrt{(-1)^2+t^2+(1-t)^2}& \\[5pt]
&=&\sqrt{1+t^2+t^2-2t+1}
\end{array}\)](https://mathjax.schullv.de/26157630221ba7c257bd76fde50fba7c6001420090031f716891e4e283339c86?color=5a5a5a)
![\(\begin{array}[t]{rll}
\,\bigg \vert \,\overrightarrow{B_tC_t}\,\bigg \vert \, &=& \left|\pmatrix{0-t\\t-1\\1-0} \right|& \\[5pt]
&=& \sqrt{(-t)^2+(t-1)^2+1^2}& \\[5pt]
&=& \sqrt{t^2+t^2-2t+1+1}
\end{array}\)](https://mathjax.schullv.de/fbccc82f3a3b0c803dd52fef476ddf73c65115c269f8c1e0c0ab4c697828c2c9?color=5a5a5a) Wegen
Wegen  gilt, dass die Dreiecke
gilt, dass die Dreiecke  folglich gleichseitig sind.
folglich gleichseitig sind.
1.3
Ebenengleichung aufstellen
Ein Stützvektor der Ebene ist beispielsweise gegeben durch  Zwei Richtungsvektoren der Ebene
Zwei Richtungsvektoren der Ebene  sind
sind  und
und  Eine Ebenengleichung von
Eine Ebenengleichung von  in Parameterform folgt somit beispielsweise mit:
Parallelität nachweisen
in Parameterform folgt somit beispielsweise mit:
Parallelität nachweisen
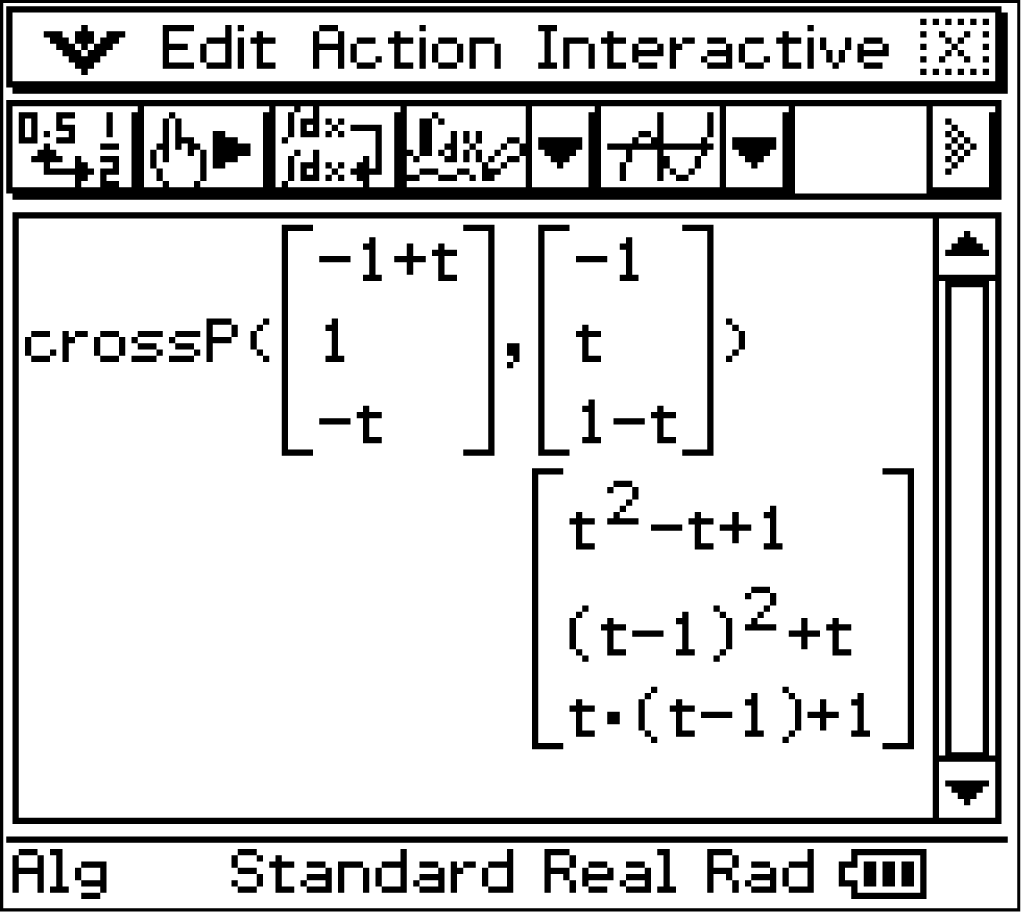 Mit dem Befehl
Mit dem Befehl  des CAS kann das Vektorprodukt der beiden Richtungsvektoren berechnet werden.
des CAS kann das Vektorprodukt der beiden Richtungsvektoren berechnet werden.
 Ein Normalenvektor folgt also mit:
Ein Normalenvektor folgt also mit:
 Die Normalenvektoren
Die Normalenvektoren  sind für alle Werte von
sind für alle Werte von  Vielfache voneinander. Folglich sind alle Ebenen
Vielfache voneinander. Folglich sind alle Ebenen  parallel zueinander.
Abstand berechnen
Koordinatenform von
parallel zueinander.
Abstand berechnen
Koordinatenform von  aufstellen:
Einsetzen der Koordinaten von
aufstellen:
Einsetzen der Koordinaten von  liefert:
liefert:
![\(\begin{array}[t]{rll}
E_t: (t^2-t+1)\cdot (1+0+t)&=& d & \\[5pt]
t^2-t+1+ (t^2-t+1)\cdot t&=& d & \\[5pt]
t^3+1&=& d
\end{array}\)](https://mathjax.schullv.de/a3163dcff9d5b82571804132a97981e07e86aa74e67df1987eb0b35b8b6e7796?color=5a5a5a) Die Hesse'sche Normalform ergibt sich zu:
Ein Stützvektors von
Die Hesse'sche Normalform ergibt sich zu:
Ein Stützvektors von  ist beispielsweise
ist beispielsweise  Es folgt also:
Der Abstand zwischen zwei Ebenen
Es folgt also:
Der Abstand zwischen zwei Ebenen  und
und  beträgt somit
beträgt somit  Längeneinheiten.
Längeneinheiten.

1.4
Flächeninhalt bestimmen
Der Betrag des Kreuzprodukts zweier Vektoren entspricht dem Flächeninhalt des von den Vektoren aufgespannten Parallelogramms. Da es sich um ein Dreieck handelt, muss dieser halbiert werden.
Mit den Vektoren  und
und  sowie deren Kreuzprodukt aus Aufgabe 1.3 ergibt sich die Funktion
sowie deren Kreuzprodukt aus Aufgabe 1.3 ergibt sich die Funktion  die den Flächeninhalt des Dreiecks in Abhängigkeit von
die den Flächeninhalt des Dreiecks in Abhängigkeit von  beschreibt.
Minimalen Flächeninhalt untersuchen
Notwendige Bedingung für Extremstellen anwenden:
beschreibt.
Minimalen Flächeninhalt untersuchen
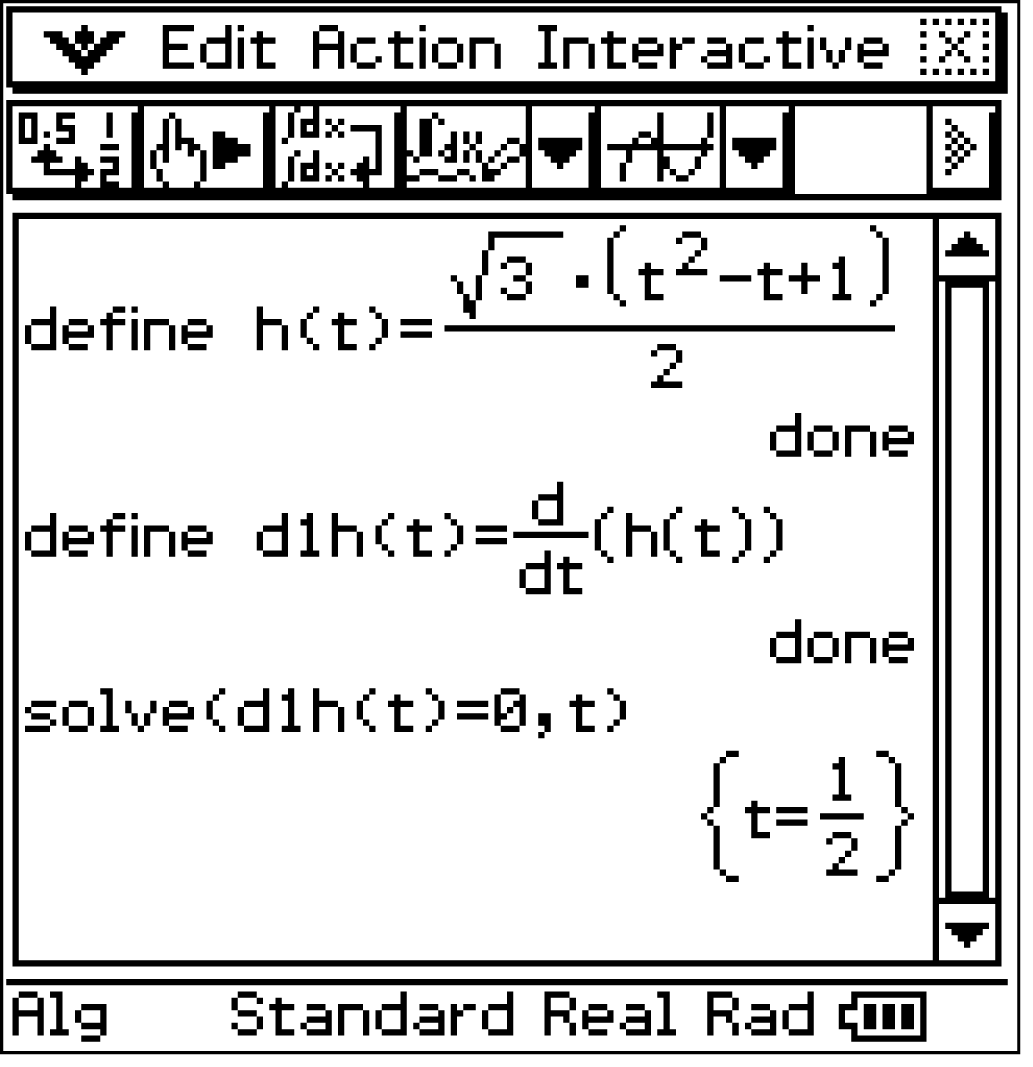
Notwendige Bedingung für Extremstellen anwenden:
 Hinreichende Bedingung für Extremstellen anwenden:
Hinreichende Bedingung für Extremstellen anwenden:
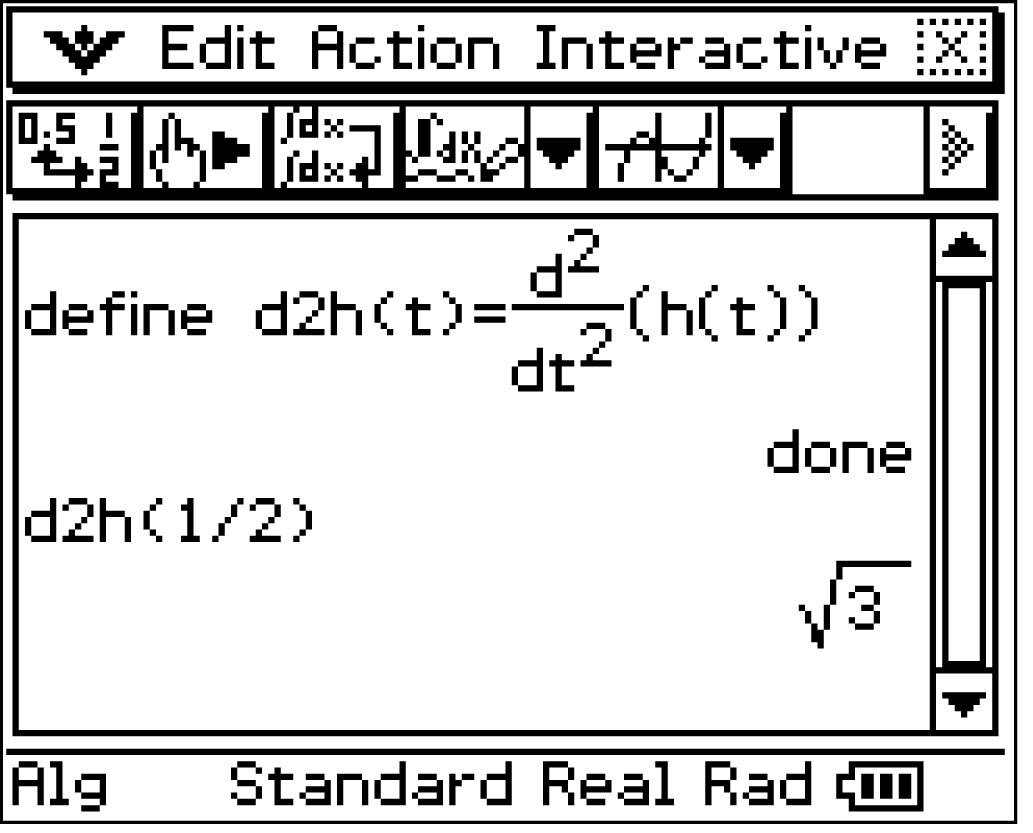 Das Dreieck
Das Dreieck  besitzt somit für
besitzt somit für  einen minimalen Flächeninhalt.
einen minimalen Flächeninhalt.
Mit dem CAS kann die erste Ableitung  der Funktion
der Funktion  bestimmt werden.
bestimmt werden.
 \to
\to  \to
\to  Mit dem
Mit dem  -Befehl folgt nun:
-Befehl folgt nun:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/49bd74442e24948e9744a756300fc5f0377e1004e5c06c648172cf3efd13f395?color=5a5a5a)

Erneutes Ableiten von  liefert die zweite Ableitung
liefert die zweite Ableitung  Es gilt:
Es gilt:


2
Gleichung bestätigen
Es gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{u_0}&=& \overrightarrow{b_0}-\overrightarrow{a_0}&\\[5pt]
&=& \pmatrix{0\\1\\0}-\pmatrix{1\\0\\0}&\\[5pt]
&=& \pmatrix{-1\\1\\0}
\end{array}\)](https://mathjax.schullv.de/f2ffebba78c5ecc3d6c2ae0cf04d4baef762fe510f7eb664ad0ade6ba738a06e?color=5a5a5a)
![\(\begin{array}[t]{rll}
\overrightarrow{u_t}&=&\overrightarrow{b_t}-\overrightarrow{a_t} &\\[5pt]
&=& \pmatrix{t\\1\\0}-\pmatrix{1\\0\\t}&\\[5pt]
&=& \pmatrix{t-1\\1\\-t}
\end{array}\)](https://mathjax.schullv.de/69ec6497e8261b807967f6c6e0c84b74d6c7a29dd9e3f184475b8bc217ecf3a5?color=5a5a5a) Somit folgt:
Somit ist die Behauptung aus der Aufgabenstellung gezeigt.
Bewegung beschreiben
Mit dem CAS kann der Graph der Funktion
Somit folgt:
Somit ist die Behauptung aus der Aufgabenstellung gezeigt.
Bewegung beschreiben
Mit dem CAS kann der Graph der Funktion  gezeichnet werden.
gezeichnet werden.
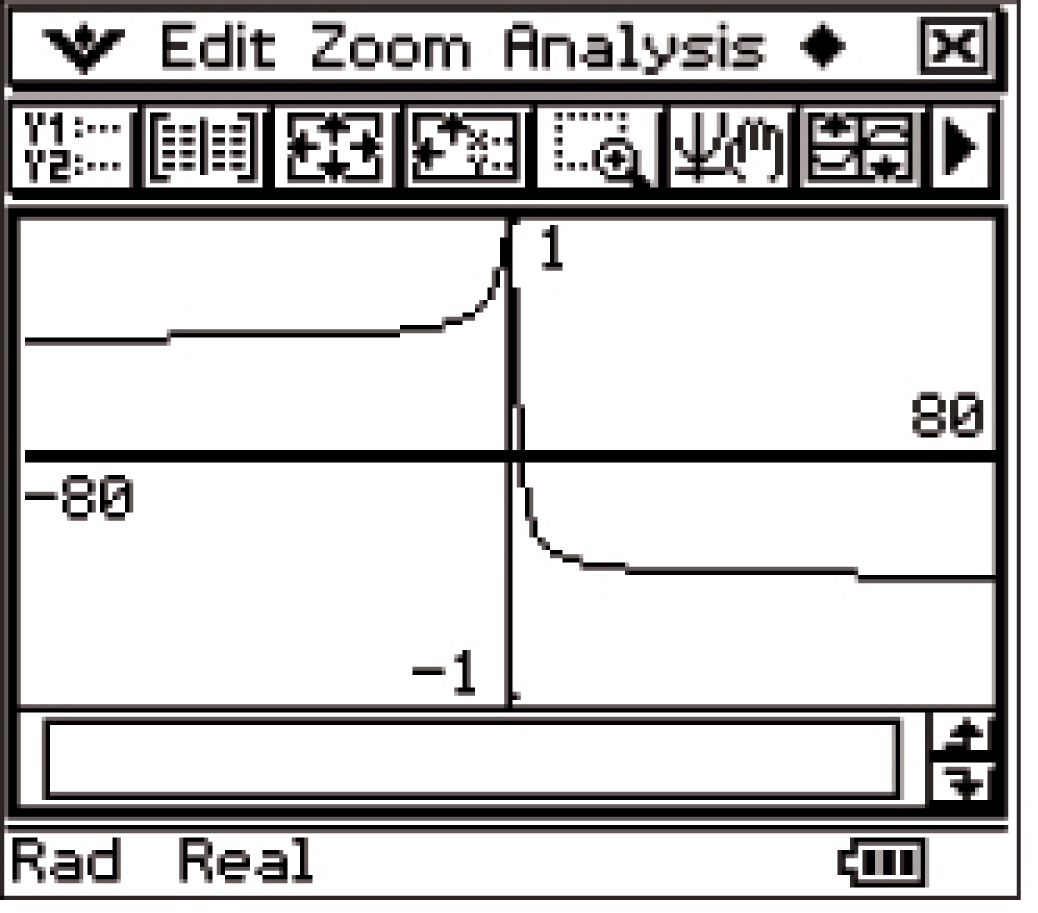
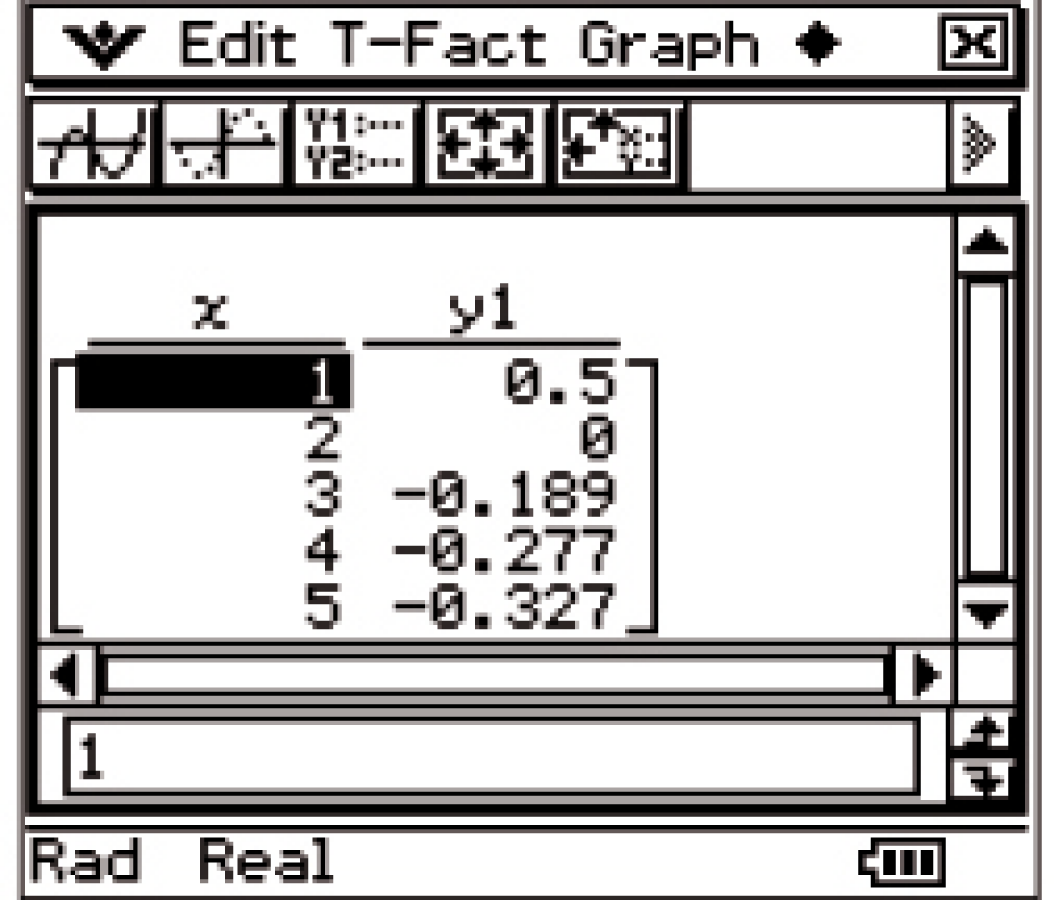 Für betragsmäßig große negative
Für betragsmäßig große negative  -Werte gilt:
-Werte gilt:
![\(\begin{array}[t]{rll}
\cos (\varphi(t))&\approx& 0,5 &\quad \scriptsize \mid\; \cos^{-1}\\[5pt]
\varphi(t)&\approx& 60^\circ
\end{array}\)](https://mathjax.schullv.de/216f65c5f6df8a586e3bf283a544c2d56f3f504896a5d57558b32a9879650c7c?color=5a5a5a) Für betragsmäßig große positive
Für betragsmäßig große positive  -Werte gilt:
-Werte gilt:
![\(\begin{array}[t]{rll}
\cos (\varphi(t))&\approx& -0,5 &\quad \scriptsize \mid\; \cos^{-1}\\[5pt]
\varphi(t)&\approx& 120^\circ
\end{array}\)](https://mathjax.schullv.de/1b8f5ad9aa4b1c3f266188dee335b98e782167e23626ec8f0f57ddcf7a5e4f90?color=5a5a5a) Hinweis: Hierbei muss beachtet werden, dass nicht
Hinweis: Hierbei muss beachtet werden, dass nicht  sondern
sondern  eingestellt ist, da der Winkel berechnet wird.
Für größer werdende negative
eingestellt ist, da der Winkel berechnet wird.
Für größer werdende negative  -Werte nähert sich der Rotationswinkel folglich
-Werte nähert sich der Rotationswinkel folglich  und für größer werdende positive
und für größer werdende positive  -Werte
-Werte  an.
Dem Schaubild aus Aufgabe 1.2 kann entnommen werden, dass die Dreiecke im Uhrzeigersinn rotieren. Beispielsweise ist der Vektor
an.
Dem Schaubild aus Aufgabe 1.2 kann entnommen werden, dass die Dreiecke im Uhrzeigersinn rotieren. Beispielsweise ist der Vektor  im Vergleich zum Vektor
im Vergleich zum Vektor  nach rechts gedreht.
Aus Aufgabe 1.3 folgt:
nach rechts gedreht.
Aus Aufgabe 1.3 folgt:
 im Uhrzeigersinn um den Vektor
im Uhrzeigersinn um den Vektor  sind parallel zueinander und der Abstand zwischen den Dreiecken wird für größer werdende
sind parallel zueinander und der Abstand zwischen den Dreiecken wird für größer werdende  ebenfalls immer größer.
ebenfalls immer größer.


- Die Dreiecke
sind alle parallel zueinander.
- Der Abstand zwischen den Dreiecken wird immer größer: