B1 - Analytische Geometrie
Für Lichtstrahlen, die auf einen ebenen Spiegel treffen, gilt das Reflexionsgesetz „Einfallswinkel gleich Reflexionswinkel“.
Die Gerade, die orthogonal zur Spiegelebene durch den Punkt verläuft, in dem der einfallende Lichtstrahl auf den Spiegel trifft, bezeichnet man als Einfallslot. Der einfallende Strahl, der reflektierte Strahl und das Einfallslot liegen in einer Ebene, die senkrecht auf der Spiegelebene steht. Im Punkt sendet ein Laser einen Lichtstrahl zum Punkt
sendet ein Laser einen Lichtstrahl zum Punkt  , der in einem ebenen Spiegel liegt. Der Spiegel soll so ausgerichtet werden, dass der Lichtstrahl zum Punkt
, der in einem ebenen Spiegel liegt. Der Spiegel soll so ausgerichtet werden, dass der Lichtstrahl zum Punkt  reflektiert wird (Material). Der Einfallswinkel zwischen
reflektiert wird (Material). Der Einfallswinkel zwischen  und dem Einfallslot sowie der Reflexionswinkel zwischen dem Einfallslot und
und dem Einfallslot sowie der Reflexionswinkel zwischen dem Einfallslot und  sind mit
sind mit  bezeichnet.
bezeichnet.
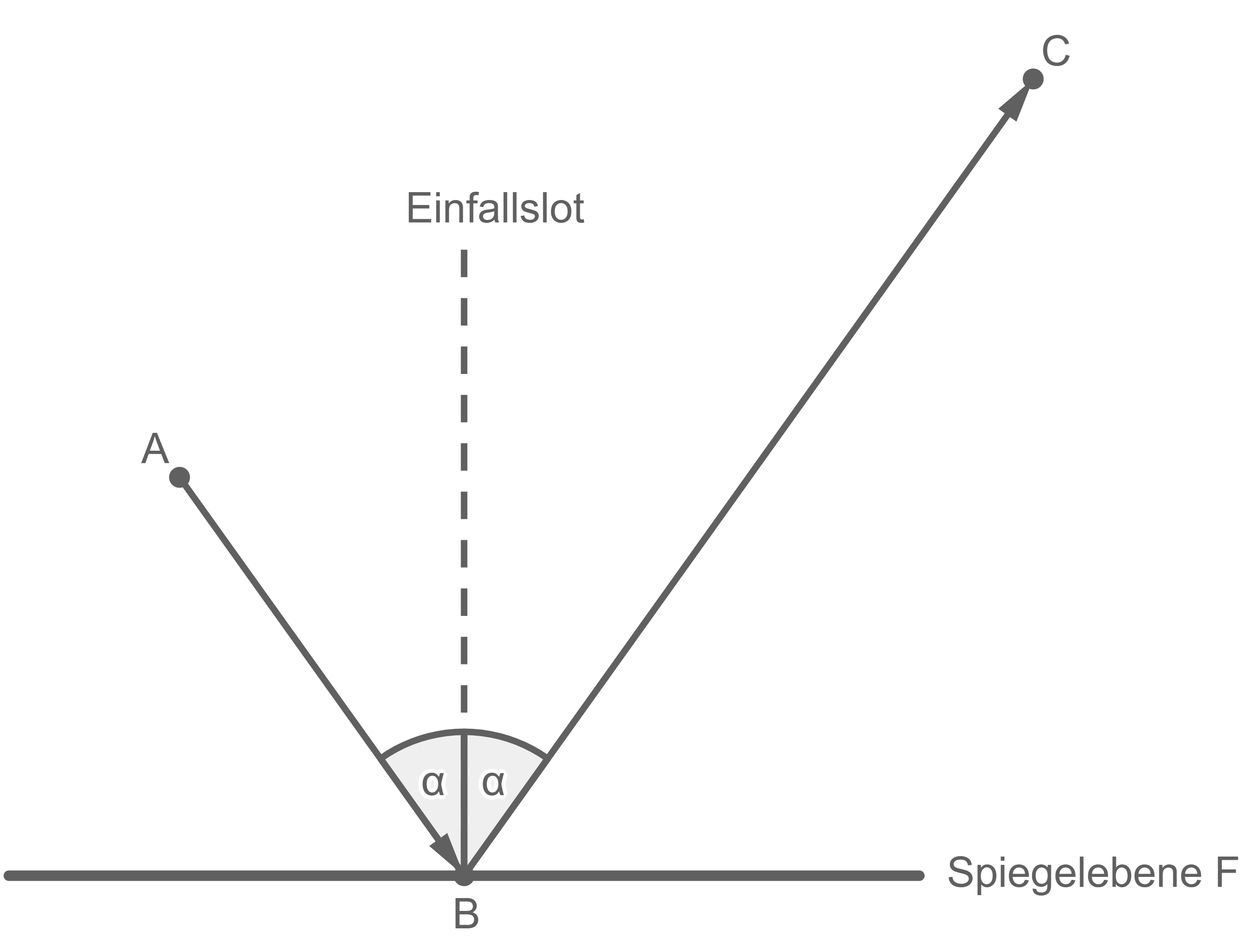
Die Gerade, die orthogonal zur Spiegelebene durch den Punkt verläuft, in dem der einfallende Lichtstrahl auf den Spiegel trifft, bezeichnet man als Einfallslot. Der einfallende Strahl, der reflektierte Strahl und das Einfallslot liegen in einer Ebene, die senkrecht auf der Spiegelebene steht. Im Punkt
1.1
Berechne die Längen der Vektoren  und
und  und zeige, dass gilt:
und zeige, dass gilt: 
(3 BE)
1.2
Berechne den Vektor 

 der die Richtung des Einfallslots angibt.
der die Richtung des Einfallslots angibt.
Bestimme den Einfallswinkel des Lichtstrahls sowie eine Koordinatengleichung der Spiegelebene .
.
 zur Kontrolle:
zur Kontrolle:  ist eine mögliche Koordinatengleichung von
ist eine mögliche Koordinatengleichung von ![\(F.]\)](https://mathjax.schullv.de/0f4e7922597c8da9b811be7b6bf614d863cc60f7ba3128e74637c9ccc0ec3a29?color=5a5a5a)
Bestimme den Einfallswinkel des Lichtstrahls sowie eine Koordinatengleichung der Spiegelebene
(6 BE)
1.3
Gegeben ist eine Gerade 

 Untersuche die besondere Lage von
Untersuche die besondere Lage von  in Bezug auf die Ebene, die durch die Punkte
in Bezug auf die Ebene, die durch die Punkte 
 und
und  gegeben ist.
gegeben ist.
(4 BE)
1.4
Deute die Zeilen  bis
bis  im folgenden Kasten im Sachzusammenhang:
im folgenden Kasten im Sachzusammenhang:
![\(\begin{array}[t]{rll}
(IV)&& \overrightarrow{a}+2\cdot\overrightarrow{AD}=\begin{pmatrix} 8\\3\\4 \end{pmatrix};\; P(8\mid3\mid4)
\end{array}\)](https://mathjax.schullv.de/80a14871ec50f6ed2b0d24f759396948547621c1d2d5cdb5e918d42f20922de9?color=5a5a5a)
(5 BE)
2.
Durch Drehung der Spiegelebene  um die Gerade
um die Gerade  aus Aufgabe 1.3 entsteht die Ebenenschar
aus Aufgabe 1.3 entsteht die Ebenenschar








2.1
Zeige, dass die Gerade  sowohl in der Ebene
sowohl in der Ebene  liegt als auch gemeinsame Gerade aller Ebenen der Ebenenschar
liegt als auch gemeinsame Gerade aller Ebenen der Ebenenschar  ist, dass aber
ist, dass aber  selbst nicht zur Ebenenschar
selbst nicht zur Ebenenschar  gehört.
gehört.
(6 BE)
2.2
Der Lichtstrahl von  nach
nach  soll in sich selbst reflektiert werden. Ermittle eine Koordinatengleichung der zugehörigen Spiegelebene aus der Ebenenschar
soll in sich selbst reflektiert werden. Ermittle eine Koordinatengleichung der zugehörigen Spiegelebene aus der Ebenenschar  und erläutere deinen Ansatz.
und erläutere deinen Ansatz.
Material
(6 BE)

1.1
Die Länge der Vektoren  und
und  berechnen
berechnen


![\(\begin{array}[t]{rll}
\mid \overrightarrow{BA} \mid&=& \sqrt{(-1)^2+5^2+6^2} \\[5pt]
&=& \sqrt{62} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/183797b7bdf1487813b109939b809ab3bf8be67a13060c85bcdcc6b06aac5caf?color=5a5a5a)
![\(\begin{array}[t]{rll}
\mid\overrightarrow{BC} \mid&=& \sqrt{10^2+2^2+12^2} \\[5pt]
&=& \sqrt{248} \\[5pt]
&=& \sqrt{4\cdot 62} \\[5pt]
&=& 2\cdot\sqrt{62} \\[5pt]
&=& 2\cdot\mid\overrightarrow{BA} \mid\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b375052664da663f8ae0b0f104aa3fee946dd7c6ebf36c806927501ee36cbfc4?color=5a5a5a) Damit ist gezeigt:
Damit ist gezeigt:  .
.
1.2
1. Den Vektor  berechnen
berechnen

![\(\begin{array}[t]{rll}
\overrightarrow{v}&=& \pmatrix{-1 \\ 5 \\ 6} + \frac{1}{2} \cdot \pmatrix{10 \\ 2 \\ 12}\\[5pt]
&=& \pmatrix{-1 \\ 5 \\ 6} + \pmatrix{5 \\ 1 \\ 6}\\[5pt]
&=& \pmatrix{4 \\ 6 \\ 12} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/91c373dabb704310adbbb7b9e7feb7a007c0255a93039fcd295166e554fdf502?color=5a5a5a) 2. Einfallswinkel des Lichtstrahls bestimmen
Da der Vektor
2. Einfallswinkel des Lichtstrahls bestimmen
Da der Vektor  die Richtung des Einfallslots angibt, ist der Einfallswinkel der Winkel zwischen dem Vektor
die Richtung des Einfallslots angibt, ist der Einfallswinkel der Winkel zwischen dem Vektor  und dem Vektor des Lichtstrahls
und dem Vektor des Lichtstrahls  .
.
Allgemein gilt für einen Winkel zwischen den Vektoren
zwischen den Vektoren  und
und  :
:

1. Schritt: Skalarprodukt der Vektoren und
und  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overrightarrow{v} \cdot \overrightarrow{BA} &=& \pmatrix{4 \\ 6 \\ 12} \cdot \pmatrix{-1 \\ 5 \\ 6}\\[5pt]
&=& 4 \cdot (-1) +6 \cdot 5 + 12 \cdot 6\\[5pt]
&=& -4 + 30 + 72 \\[5pt]
&=& 98 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e5ad52fe0e0c551a401322ace39d01ee2c90430177c37a23586e7623ae6498ad?color=5a5a5a) 2. Schritt: Beträge der Vektoren berechnen
2. Schritt: Beträge der Vektoren berechnen
![\(\begin{array}[t]{rll}
\mid \overrightarrow{v} \mid&=& \sqrt{4^2+6^2+12^2} \\[5pt]
&=& \sqrt{196} \\[5pt]
&=& 14 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/aa83291f420c41c529586a2ca40bb156f841a3304473493dac187716dfc3934c?color=5a5a5a) Der Betrag des Vektors
Der Betrag des Vektors  kann aus der vorigen Aufgaben übernommen werden:
kann aus der vorigen Aufgaben übernommen werden:  .
3. Schritt: Einfallswinkel
.
3. Schritt: Einfallswinkel  berechnen
Mit dem CAS wird nun der Einfallswinkel berechnet:
berechnen
Mit dem CAS wird nun der Einfallswinkel berechnet:
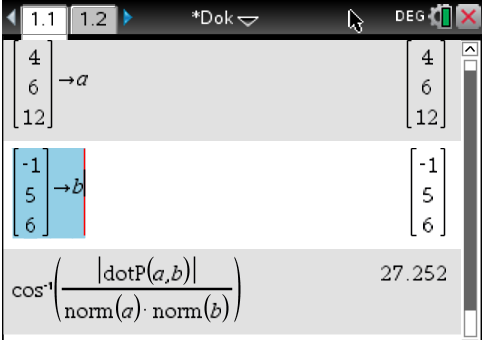 Der vom CAS berechnete Einfallswinkel beträgt damit
Der vom CAS berechnete Einfallswinkel beträgt damit  3. Koordinatengleichung der Spiegelebene bestimmen
Für die Koordinatengleichung wird ein Normalenvektor
3. Koordinatengleichung der Spiegelebene bestimmen
Für die Koordinatengleichung wird ein Normalenvektor  benötigt, der senkrecht zu der Ebene
benötigt, der senkrecht zu der Ebene  steht und ein Punkt, der in der Ebene liegt.
steht und ein Punkt, der in der Ebene liegt.

Da das Einfallslot senkrecht auf der Spiegelebene steht, kann der Vektor als Normalenvektor verwendet werden.
Als Punkt, der in der Ebene liegt, kann der Punkt
als Normalenvektor verwendet werden.
Als Punkt, der in der Ebene liegt, kann der Punkt  verwendet werden
verwendet werden
Daraus folgt:



 Durch Kürzen der Gleichung mit 2 entsteht folgende Gleichung:
Durch Kürzen der Gleichung mit 2 entsteht folgende Gleichung:

Allgemein gilt für einen Winkel
1. Schritt: Skalarprodukt der Vektoren
Calculator  Menu
Menu  Matrix und Vektoren
Matrix und Vektoren  Erstellen
Erstellen  Matrix...
Matrix...  3x1
3x1  Vektorwerte eingeben
Vektorwerte eingeben  ctrl
ctrl  var
var  Vektorvariable wählen
Vektorvariable wählen  Enter
Enter  trig
trig 

 abs(dotP(Vektor1, Vektor2)/(norm(Vektor1)* norm(Vektor2)))
abs(dotP(Vektor1, Vektor2)/(norm(Vektor1)* norm(Vektor2)))  ctr
ctr  Enter
Enter

Da das Einfallslot senkrecht auf der Spiegelebene steht, kann der Vektor
Daraus folgt:
1.3
1. Schritt: Die Ebene  und die Gerade
und die Gerade  auf Schnittpunkte untersuchen
Koordinatengleichung der Ebene
auf Schnittpunkte untersuchen
Koordinatengleichung der Ebene  aufstellen, welche die Punkte
aufstellen, welche die Punkte und
und  enthält:
Als Normalenvektor
enthält:
Als Normalenvektor  der Ebene
der Ebene  kann das Kreuzprodukt aus den Vektoren
kann das Kreuzprodukt aus den Vektoren  und
und  gewählt werden.
Da der Normalenvektor von
gewählt werden.
Da der Normalenvektor von  und der Richtungsvektor von
und der Richtungsvektor von  offensichtlich Vielfache voneinander sind, bedeutet dies:
offensichtlich Vielfache voneinander sind, bedeutet dies:  und
und  schneiden sich senkrecht. Da der Stützvektor von
schneiden sich senkrecht. Da der Stützvektor von  der Ortsvekor
der Ortsvekor  ist, bedeutet dies für die Lage der Ebene und der Gerade, dass sich die Ebene
ist, bedeutet dies für die Lage der Ebene und der Gerade, dass sich die Ebene  und die Gerade
und die Gerade  senkrecht im Punkt
senkrecht im Punkt  schneiden.
schneiden.
1.4
Die Zeilen  bis
bis  kann man als Verfahren deuten, bei dem derjenige Punkt ermittelt wird, der durch Spiegelung des Punktes
kann man als Verfahren deuten, bei dem derjenige Punkt ermittelt wird, der durch Spiegelung des Punktes  an dem Einfallslot entsteht.
Gleichung
an dem Einfallslot entsteht.
Gleichung  Dabei wird in Gleichung
Dabei wird in Gleichung  eine Geradengleichung
eine Geradengleichung  für das Einfallslot aufgestellt. Diese enthält als Stützvektor den Ortsvektor
für das Einfallslot aufgestellt. Diese enthält als Stützvektor den Ortsvektor  und als Richtungsvektor den Vektor
und als Richtungsvektor den Vektor  gekürzt mit 2.
Gleichung
gekürzt mit 2.
Gleichung 
In Gleichung wird dann eine Hilfsebene aufgestellt, die die Gerade
wird dann eine Hilfsebene aufgestellt, die die Gerade  senkrecht schneidet und den Punkt
senkrecht schneidet und den Punkt  enthält. Dies erkennt man daran, dass der Richtungsvektor von
enthält. Dies erkennt man daran, dass der Richtungsvektor von  und der Normalenvektor von
und der Normalenvektor von  übereinstimmen. Außerdem wurde als Ortsvektor der Vektor
übereinstimmen. Außerdem wurde als Ortsvektor der Vektor  , gewählt, was verdeutlicht, dass die Ebene
, gewählt, was verdeutlicht, dass die Ebene  den Punkt
den Punkt  enthält.
Gleichung
enthält.
Gleichung 
In Gleichung wird nun der Schnittpunkt des Einfallslots an der Hilfsebene
wird nun der Schnittpunkt des Einfallslots an der Hilfsebene  berechnet, indem ein allgemeiner Punkt
berechnet, indem ein allgemeiner Punkt  der Geraden
der Geraden  in die Koordinatengleichung der Ebene
in die Koordinatengleichung der Ebene  eingesetzt wird. Als Ergebnis erhält man den Schnittpunkt
eingesetzt wird. Als Ergebnis erhält man den Schnittpunkt  .
Gleichung
.
Gleichung Der Spiegelpunkt
Der Spiegelpunkt  lässt sich nun durch den Vektorzug in Gleichung
lässt sich nun durch den Vektorzug in Gleichung  berechnen. Dabei sollen
berechnen. Dabei sollen  und
und  den selben Abstand zur Ebene haben, weswegen
den selben Abstand zur Ebene haben, weswegen  gerechnet wird.
gerechnet wird.
In Gleichung
In Gleichung
2.1
1.Zeigen, dass die Gerade  in der Ebene
in der Ebene  liegt
Allgeminer Punkt
liegt
Allgeminer Punkt  der Geraden
der Geraden  bestimmen
bestimmen
 Koordinaten des Punktes
Koordinaten des Punktes  in die Koordinatengleichung von
in die Koordinatengleichung von  einsetzen:
Die Gleichung ist also unabhängig von
einsetzen:
Die Gleichung ist also unabhängig von  erfüllt, woraus folgt, dass
erfüllt, woraus folgt, dass  in
in  liegt.
2.Zeigen, dass
liegt.
2.Zeigen, dass  als gemeinsame Gerade in
als gemeinsame Gerade in  liegt
Allgemeiner Punkt
liegt
Allgemeiner Punkt  der Geraden
der Geraden  in die Koordinatengleichung der Ebenenschar
in die Koordinatengleichung der Ebenenschar  einsetzen:
Die Gleichung ist also für alle
einsetzen:
Die Gleichung ist also für alle  und alle
und alle  erfüllt, woraus folgt, dass die Gerade
erfüllt, woraus folgt, dass die Gerade  gemeinsame Gerade der Ebenenschar
gemeinsame Gerade der Ebenenschar  ist.
3.Zeigen, dass die Ebene
ist.
3.Zeigen, dass die Ebene  nicht zur Ebenenschar
nicht zur Ebenenschar  gehört
Würde
gehört
Würde  zu
zu  gehören, müssetn die Faktoren in der Koordinatengleichung von
gehören, müssetn die Faktoren in der Koordinatengleichung von  und
und  vor
vor  und
und  übereinstimmen.
Es müsste also gelten:
übereinstimmen.
Es müsste also gelten:

![\(\begin{array}{}
\text{I}\quad&4,5+3a&=& 4 \quad \scriptsize\mid\; -4,5\\[5pt]
& 3a &=& -0,5\quad \scriptsize\mid\; :3 \\[5pt]
& a &=& -\frac{1}{6} \\[5pt]
\text{II}\quad&4,5a-3&=& 6 \quad \scriptsize\mid\; +3\\[5pt]
& 4,5a &=& 9\quad \scriptsize\mid\; :4,5 \\[5pt]
& a &=& 2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6247f10d606e57b3ef80223b39f0085c461a49757013fe1a7f7e61ee0daebf3d?color=5a5a5a) Die erste Gleichung wäre also durch
Die erste Gleichung wäre also durch  und die zweite Gleichung durch
und die zweite Gleichung durch  erfüllt. Dadurch entsteht ein Widerspruch, was bedeutet, dass die Ebene
erfüllt. Dadurch entsteht ein Widerspruch, was bedeutet, dass die Ebene  nicht in der Ebenenschar
nicht in der Ebenenschar  liegt.
liegt.
2.2
Spiegelebene ermitteln
Damit der Lichtstrahl von  nach
nach  in sich selbst reflektiert wird, muss er senkrecht auf die Ebene treffen. Das bedeuetet der Vektor
in sich selbst reflektiert wird, muss er senkrecht auf die Ebene treffen. Das bedeuetet der Vektor  un der Normalenvekror
un der Normalenvekror  der Ebenenschar
der Ebenenschar  müssen Vielfache voneinander sein. Der Normalenvektor
müssen Vielfache voneinander sein. Der Normalenvektor  lässt sich aus der Koordinatengleichung ablesen:
lässt sich aus der Koordinatengleichung ablesen:
 Mathematisch ausgedrückt muss also gelten:
Mathematisch ausgedrückt muss also gelten:
 Das liefert folgendes Gleichungssystem:
Das liefert folgendes Gleichungssystem:
![\(\begin{array}{}
\text{I}\quad&4,5m+3am&=&-1\quad\\[5pt]
\text{II}\quad&4,5am-3m&=&5\quad \\[5pt]
\text{III}\quad&9am&=&6\quad\\[5pt]
\end{array}\)](https://mathjax.schullv.de/d40e9c16e246583dfc82cbbe19159df254b266859defecf4c1ae3373173e81c0?color=5a5a5a) Ersetzen von
Ersetzen von  durch eine dritte Variable und Eingabe wie folgt in den CAS liefert dann das Ergebnis:
durch eine dritte Variable und Eingabe wie folgt in den CAS liefert dann das Ergebnis:
 Der CAS gibt
Der CAS gibt 
 und
und 

 als Lösung zurück. Einsetzen von
als Lösung zurück. Einsetzen von  in
in  liefert für
liefert für 



 Die Spiegelebene
Die Spiegelebene  , die den Strahl wieder in sich selbst reflektiert, ist somit gegeben durch
, die den Strahl wieder in sich selbst reflektiert, ist somit gegeben durch

on  Calculator
Calculator  Menu
Menu  Algebra
Algebra  Gleichungssysteme lösen
Gleichungssysteme lösen  System linearer Gleichungen lösen...
System linearer Gleichungen lösen...  Anzahl der Gleichungen: 4
Anzahl der Gleichungen: 4  Variablen: Variablennamen mit Komma getrennt eingeben
Variablen: Variablennamen mit Komma getrennt eingeben  OK
OK

1.1
Die Länge der Vektoren  und
und  berechnen
berechnen


![\(\begin{array}[t]{rll}
\mid \overrightarrow{BA} \mid&=& \sqrt{(-1)^2+5^2+6^2} \\[5pt]
&=& \sqrt{62} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/183797b7bdf1487813b109939b809ab3bf8be67a13060c85bcdcc6b06aac5caf?color=5a5a5a)
![\(\begin{array}[t]{rll}
\mid\overrightarrow{BC} \mid&=& \sqrt{10^2+2^2+12^2} \\[5pt]
&=& \sqrt{248} \\[5pt]
&=& \sqrt{4\cdot 62} \\[5pt]
&=& 2\cdot\sqrt{62} \\[5pt]
&=& 2\cdot\mid\overrightarrow{BA} \mid\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b375052664da663f8ae0b0f104aa3fee946dd7c6ebf36c806927501ee36cbfc4?color=5a5a5a) Damit ist gezeigt:
Damit ist gezeigt:  .
.
1.2
1. Den Vektor  berechnen
berechnen

![\(\begin{array}[t]{rll}
\overrightarrow{v}&=& \pmatrix{-1 \\ 5 \\ 6} + \frac{1}{2} \cdot \pmatrix{10 \\ 2 \\ 12}\\[5pt]
&=& \pmatrix{-1 \\ 5 \\ 6} + \pmatrix{5 \\ 1 \\ 6}\\[5pt]
&=& \pmatrix{4 \\ 6 \\ 12} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/91c373dabb704310adbbb7b9e7feb7a007c0255a93039fcd295166e554fdf502?color=5a5a5a) 2. Einfallswinkel des Lichtstrahls bestimmen
Da der Vektor
2. Einfallswinkel des Lichtstrahls bestimmen
Da der Vektor  die Richtung des Einfallslots angibt, ist der Einfallswinkel der Winkel zwischen dem Vektor
die Richtung des Einfallslots angibt, ist der Einfallswinkel der Winkel zwischen dem Vektor  und dem Vektor des Lichtstrahls
und dem Vektor des Lichtstrahls  .
.
Allgemein gilt für einen Winkel zwischen den Vektoren
zwischen den Vektoren  und
und  :
:

1. Schritt: Skalarprodukt der Vektoren und
und  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overrightarrow{v} \cdot \overrightarrow{BA} &=& \pmatrix{4 \\ 6 \\ 12} \cdot \pmatrix{-1 \\ 5 \\ 6}\\[5pt]
&=& 4 \cdot (-1) +6 \cdot 5 + 12 \cdot 6\\[5pt]
&=& -4 + 30 + 72 \\[5pt]
&=& 98 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e5ad52fe0e0c551a401322ace39d01ee2c90430177c37a23586e7623ae6498ad?color=5a5a5a) 2. Schritt: Beträge der Vektoren berechnen
2. Schritt: Beträge der Vektoren berechnen
![\(\begin{array}[t]{rll}
\mid \overrightarrow{v} \mid&=& \sqrt{4^2+6^2+12^2} \\[5pt]
&=& \sqrt{196} \\[5pt]
&=& 14 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/aa83291f420c41c529586a2ca40bb156f841a3304473493dac187716dfc3934c?color=5a5a5a) Der Betrag des Vektors
Der Betrag des Vektors  kann aus der vorigen Aufgaben übernommen werden:
kann aus der vorigen Aufgaben übernommen werden:  .
3. Schritt: Einfallswinkel
.
3. Schritt: Einfallswinkel  berechnen
Mit dem CAS wird nun der Einfallswinkel berechnet:
berechnen
Mit dem CAS wird nun der Einfallswinkel berechnet:
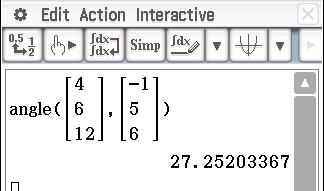 Der vom CAS berechnete Einfallswinkel beträgt damit
Der vom CAS berechnete Einfallswinkel beträgt damit  3. Koordinatengleichung der Spiegelebene bestimmen
Für die Koordinatengleichung wird ein Normalenvektor
3. Koordinatengleichung der Spiegelebene bestimmen
Für die Koordinatengleichung wird ein Normalenvektor  benötigt, der senkrecht zu der Ebene
benötigt, der senkrecht zu der Ebene  steht und ein Punkt, der in der Ebene liegt.
steht und ein Punkt, der in der Ebene liegt.

Da das Einfallslot senkrecht auf der Spiegelebene steht, kann der Vektor als Normalenvektor verwendet werden.
Als Punkt, der in der Ebene liegt, kann der Punkt
als Normalenvektor verwendet werden.
Als Punkt, der in der Ebene liegt, kann der Punkt  verwendet werden
verwendet werden
Daraus folgt:



 Durch Kürzen der Gleichung mit 2 entsteht folgende Gleichung:
Durch Kürzen der Gleichung mit 2 entsteht folgende Gleichung:

Allgemein gilt für einen Winkel
1. Schritt: Skalarprodukt der Vektoren
Action  Vektor
Vektor  angle(Vektor1, Vektor2)
angle(Vektor1, Vektor2)  ENTER
ENTER

Da das Einfallslot senkrecht auf der Spiegelebene steht, kann der Vektor
Daraus folgt:
1.3
1. Schritt: Die Ebene  und die Gerade
und die Gerade  auf Schnittpunkte untersuchen
Koordinatengleichung der Ebene
auf Schnittpunkte untersuchen
Koordinatengleichung der Ebene  aufstellen, welche die Punkte
aufstellen, welche die Punkte und
und  enthält:
Als Normalenvektor
enthält:
Als Normalenvektor  der Ebene
der Ebene  kann das Kreuzprodukt aus den Vektoren
kann das Kreuzprodukt aus den Vektoren  und
und  gewählt werden.
Da der Normalenvektor von
gewählt werden.
Da der Normalenvektor von  und der Richtungsvektor von
und der Richtungsvektor von  offensichtlich Vielfache voneinander sind, bedeutet dies:
offensichtlich Vielfache voneinander sind, bedeutet dies:  und
und  schneiden sich senkrecht. Da der Stützvektor von
schneiden sich senkrecht. Da der Stützvektor von  der Ortsvekor
der Ortsvekor  ist, bedeutet dies für die Lage der Ebene und der Gerade, dass sich die Ebene
ist, bedeutet dies für die Lage der Ebene und der Gerade, dass sich die Ebene  und die Gerade
und die Gerade  senkrecht im Punkt
senkrecht im Punkt  schneiden.
schneiden.
1.4
Die Zeilen  bis
bis  kann man als Verfahren deuten, bei dem derjenige Punkt ermittelt wird, der durch Spiegelung des Punktes
kann man als Verfahren deuten, bei dem derjenige Punkt ermittelt wird, der durch Spiegelung des Punktes  an dem Einfallslot entsteht.
Gleichung
an dem Einfallslot entsteht.
Gleichung  Dabei wird in Gleichung
Dabei wird in Gleichung  eine Geradengleichung
eine Geradengleichung  für das Einfallslot aufgestellt. Diese enthält als Stützvektor den Ortsvektor
für das Einfallslot aufgestellt. Diese enthält als Stützvektor den Ortsvektor  und als Richtungsvektor den Vektor
und als Richtungsvektor den Vektor  gekürzt mit 2.
Gleichung
gekürzt mit 2.
Gleichung 
In Gleichung wird dann eine Hilfsebene aufgestellt, die die Gerade
wird dann eine Hilfsebene aufgestellt, die die Gerade  senkrecht schneidet und den Punkt
senkrecht schneidet und den Punkt  enthält. Dies erkennt man daran, dass der Richtungsvektor von
enthält. Dies erkennt man daran, dass der Richtungsvektor von  und der Normalenvektor von
und der Normalenvektor von  übereinstimmen. Außerdem wurde als Ortsvektor der Vektor
übereinstimmen. Außerdem wurde als Ortsvektor der Vektor  , gewählt, was verdeutlicht, dass die Ebene
, gewählt, was verdeutlicht, dass die Ebene  den Punkt
den Punkt  enthält.
Gleichung
enthält.
Gleichung 
In Gleichung wird nun der Schnittpunkt des Einfallslots an der Hilfsebene
wird nun der Schnittpunkt des Einfallslots an der Hilfsebene  berechnet, indem ein allgemeiner Punkt
berechnet, indem ein allgemeiner Punkt  der Geraden
der Geraden  in die Koordinatengleichung der Ebene
in die Koordinatengleichung der Ebene  eingesetzt wird. Als Ergebnis erhält man den Schnittpunkt
eingesetzt wird. Als Ergebnis erhält man den Schnittpunkt  .
Gleichung
.
Gleichung Der Spiegelpunkt
Der Spiegelpunkt  lässt sich nun durch den Vektorzug in Gleichung
lässt sich nun durch den Vektorzug in Gleichung  berechnen. Dabei sollen
berechnen. Dabei sollen  und
und  den selben Abstand zur Ebene haben, weswegen
den selben Abstand zur Ebene haben, weswegen  gerechnet wird.
gerechnet wird.
In Gleichung
In Gleichung
2.1
1.Zeigen, dass die Gerade  in der Ebene
in der Ebene  liegt
Allgeminer Punkt
liegt
Allgeminer Punkt  der Geraden
der Geraden  bestimmen
bestimmen
 Koordinaten des Punktes
Koordinaten des Punktes  in die Koordinatengleichung von
in die Koordinatengleichung von  einsetzen:
Die Gleichung ist also unabhängig von
einsetzen:
Die Gleichung ist also unabhängig von  erfüllt, woraus folgt, dass
erfüllt, woraus folgt, dass  in
in  liegt.
2.Zeigen, dass
liegt.
2.Zeigen, dass  als gemeinsame Gerade in
als gemeinsame Gerade in  liegt
Allgemeiner Punkt
liegt
Allgemeiner Punkt  der Geraden
der Geraden  in die Koordinatengleichung der Ebenenschar
in die Koordinatengleichung der Ebenenschar  einsetzen:
Die Gleichung ist also für alle
einsetzen:
Die Gleichung ist also für alle  und alle
und alle  erfüllt, woraus folgt, dass die Gerade
erfüllt, woraus folgt, dass die Gerade  gemeinsame Gerade der Ebenenschar
gemeinsame Gerade der Ebenenschar  ist.
3.Zeigen, dass die Ebene
ist.
3.Zeigen, dass die Ebene  nicht zur Ebenenschar
nicht zur Ebenenschar  gehört
Würde
gehört
Würde  zu
zu  gehören, müssetn die Faktoren in der Koordinatengleichung von
gehören, müssetn die Faktoren in der Koordinatengleichung von  und
und  vor
vor  und
und  übereinstimmen.
Es müsste also gelten:
übereinstimmen.
Es müsste also gelten:

![\(\begin{array}{}
\text{I}\quad&4,5+3a&=& 4 \quad \scriptsize\mid\; -4,5\\[5pt]
& 3a &=& -0,5\quad \scriptsize\mid\; :3 \\[5pt]
& a &=& -\frac{1}{6} \\[5pt]
\text{II}\quad&4,5a-3&=& 6 \quad \scriptsize\mid\; +3\\[5pt]
& 4,5a &=& 9\quad \scriptsize\mid\; :4,5 \\[5pt]
& a &=& 2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6247f10d606e57b3ef80223b39f0085c461a49757013fe1a7f7e61ee0daebf3d?color=5a5a5a) Die erste Gleichung wäre also durch
Die erste Gleichung wäre also durch  und die zweite Gleichung durch
und die zweite Gleichung durch  erfüllt. Dadurch entsteht ein Widerspruch, was bedeutet, dass die Ebene
erfüllt. Dadurch entsteht ein Widerspruch, was bedeutet, dass die Ebene  nicht in der Ebenenschar
nicht in der Ebenenschar  liegt.
liegt.
2.2
Spiegelebene ermitteln
Damit der Lichtstrahl von  nach
nach  in sich selbst reflektiert wird, muss er senkrecht auf die Ebene treffen. Das bedeuetet der Vektor
in sich selbst reflektiert wird, muss er senkrecht auf die Ebene treffen. Das bedeuetet der Vektor  un der Normalenvekror
un der Normalenvekror  der Ebenenschar
der Ebenenschar  müssen Vielfache voneinander sein. Der Normalenvektor
müssen Vielfache voneinander sein. Der Normalenvektor  lässt sich aus der Koordinatengleichung ablesen:
lässt sich aus der Koordinatengleichung ablesen:
 Mathematisch ausgedrückt muss also gelten:
Mathematisch ausgedrückt muss also gelten:
 Das liefert folgendes Gleichungssystem:
Das liefert folgendes Gleichungssystem:
![\(\begin{array}{}
\text{I}\quad&4,5m+3am&=&-1\quad\\[5pt]
\text{II}\quad&4,5am-3m&=&5\quad \\[5pt]
\text{III}\quad&9am&=&6\quad\\[5pt]
\end{array}\)](https://mathjax.schullv.de/d40e9c16e246583dfc82cbbe19159df254b266859defecf4c1ae3373173e81c0?color=5a5a5a) Eingabe wie folgt in den CAS liefert dann das Ergebnis:
Eingabe wie folgt in den CAS liefert dann das Ergebnis:
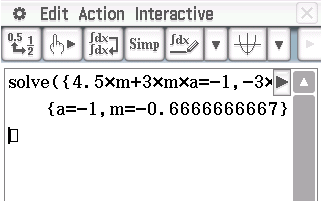 Der CAS gibt
Der CAS gibt 
 und
und 
 als Lösung zurück. Die Spiegelebene
als Lösung zurück. Die Spiegelebene  , die den Strahl wieder in sich selbst reflektiert, ist somit gegeben durch
, die den Strahl wieder in sich selbst reflektiert, ist somit gegeben durch

Action  Advanced
Advanced  solve({lin. Gleichungen}, {Variablen})
solve({lin. Gleichungen}, {Variablen})  ENTER
ENTER
