B1 - Analysis
Ein Freizeitpark öffnet an einem bestimmten Tag für seine Besucher um 9:00 Uhr und schließt um 19:00 Uhr, wobei der letzte Einlass um 17:00 Uhr erfolgt. Eingang und Ausgang erfolgen voneinander getrennt an unterschiedlichen Seiten des Parks.
 besitzt die Nullstellen
besitzt die Nullstellen  und
und  Begründe anhand des Funktionsterms ohne Rechnung, dass
Begründe anhand des Funktionsterms ohne Rechnung, dass  nicht mehr als diese zwei Nullstellen haben kann.
nicht mehr als diese zwei Nullstellen haben kann.
1
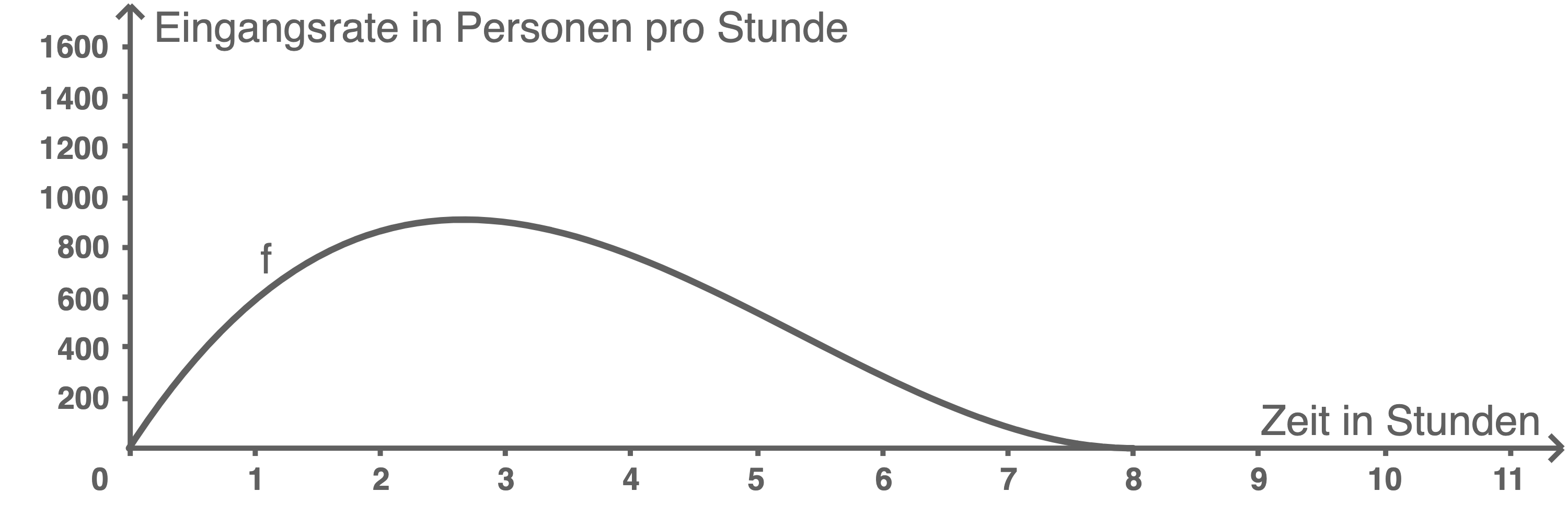
Die Eingangsrate (in Personen pro Stunde) beim Betreten des Parks lässt sich in sehr guter Näherung durch die Funktion  mit
mit  und
und  modellieren, wobei
modellieren, wobei  die Zeit in Stunden nach Öffnung des Parks angibt.
Der Graph von
die Zeit in Stunden nach Öffnung des Parks angibt.
Der Graph von  ist in der Abbildung 1 dargestellt.
ist in der Abbildung 1 dargestellt.

Abbildung 1
1.1
Berechne die Anzahl der Besucher, die gemäß der Modellierung mit der Funktion  an diesem Tag den Park betreten.
an diesem Tag den Park betreten.
 zur Kontrolle: Die Anzahl der Besucher beträgt 4096.
zur Kontrolle: Die Anzahl der Besucher beträgt 4096. ![\(\big]\)](https://mathjax.schullv.de/0c6dff9ed6a80b0cc013679b53aff551dd11abb4691ba32076d10b15d6195a5d?color=5a5a5a)
(3 BE)
1.2
Bestimme unter Angabe der Ableitungsfunktion  die Uhrzeit (in Stunden und Minuten), zu der die Eingangsrate maximal ist.
Prüfe, ob die folgende Aussage wahr oder falsch ist:
„Im Zeitraum von 9 Uhr bis 17 Uhr ist die maximale Eingangsrate um mehr als
die Uhrzeit (in Stunden und Minuten), zu der die Eingangsrate maximal ist.
Prüfe, ob die folgende Aussage wahr oder falsch ist:
„Im Zeitraum von 9 Uhr bis 17 Uhr ist die maximale Eingangsrate um mehr als  größer als die durchschnittliche Eingangsrate."
größer als die durchschnittliche Eingangsrate."
(9 BE)
1.3
Damit es keine Wartezeiten am Eingang gibt, muss zu den Zeiten, an denen die Eingangsrate mindestens 10 Personen pro Minute beträgt, ein zusätzlicher Mitarbeiter zur Verfügung stehen.
Prüfe, ob es ausreichend ist, den zusätzlichen Mitarbeiter im Zeitraum von 10:00 Uhr bis 14:00 Uhr einzubestellen.
(3 BE)
2
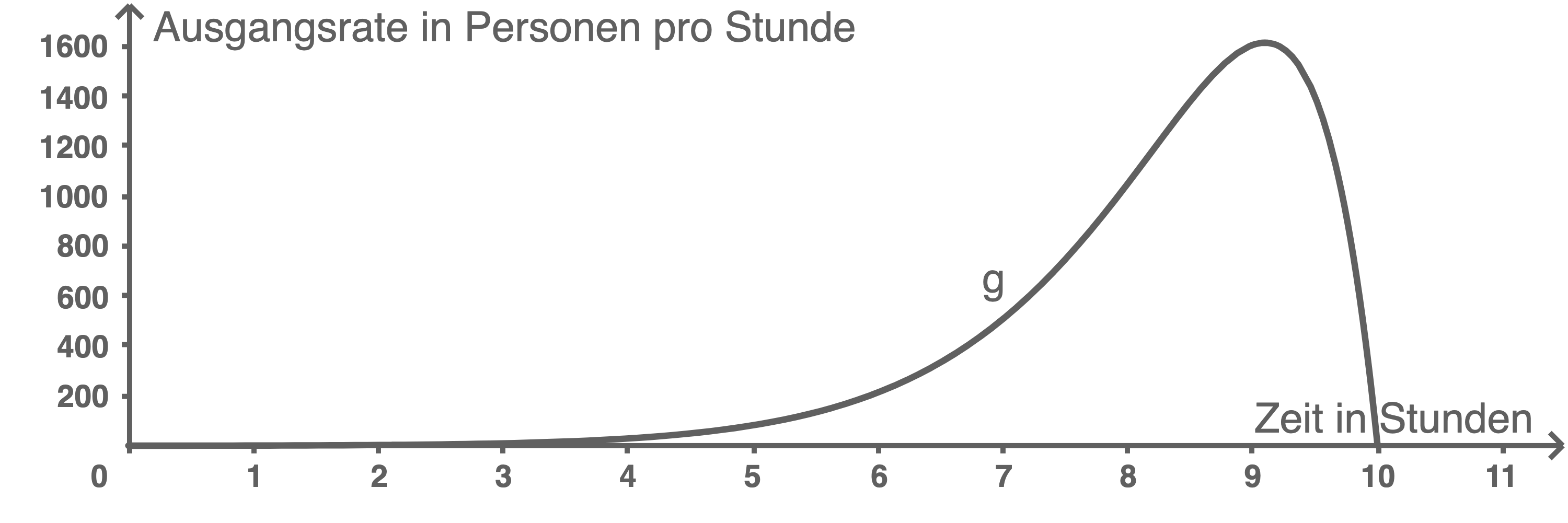
Die Ausgangsrate (in Personen pro Stunde) beim Verlassen des Parks lässt sich für  in sehr guter Näherung durch die Funktion
in sehr guter Näherung durch die Funktion  modellieren, deren Graph in Abbildung 2 dargestellt ist. Dabei gibt
modellieren, deren Graph in Abbildung 2 dargestellt ist. Dabei gibt  wie in Aufgabe 1 die Zeit in Stunden nach Öffnung des Parks an.
Die Funktion
wie in Aufgabe 1 die Zeit in Stunden nach Öffnung des Parks an.
Die Funktion  gehört zur Funktionenschar
gehört zur Funktionenschar  mit
mit  , wobei
, wobei  ist.
ist.

Abbildung 2
2.1
Beschreibe ohne Verwendung einer Rechnung den Einfluss des Parameters  auf den Verlauf der Graphen von
auf den Verlauf der Graphen von  sowie auf die Lage der Schnittpunkte mit der
sowie auf die Lage der Schnittpunkte mit der  -Achse, der Extrempunkte und der Wendepunkte der Graphen.
-Achse, der Extrempunkte und der Wendepunkte der Graphen.
(3 BE)
2.2
(2 BE)
2.3
Berechne die erste Ableitung der Funktionenschar  und zeige, dass für die zweite Ableitung gilt:
und zeige, dass für die zweite Ableitung gilt:

(4 BE)
2.4
Berechne die Wendestelle von  im Intervall
im Intervall  wobei die Untersuchung der notwendigen Bedingung genügt.
Beschreibe die Bedeutung dieser Wendestelle im Sachzusammenhang.
wobei die Untersuchung der notwendigen Bedingung genügt.
Beschreibe die Bedeutung dieser Wendestelle im Sachzusammenhang.
(5 BE)
2.5
Berechne mit Hilfe eines geeigneten Formansatzes eine Stammfunktionenschar  von
von 
(7 BE)
2.6
Es gilt  Begründe im Sachzusammenhang, warum diese Gleichung eine sinnvolle Bedingung darstellt.
Zeige rechnerisch, dass für die Funktion
Begründe im Sachzusammenhang, warum diese Gleichung eine sinnvolle Bedingung darstellt.
Zeige rechnerisch, dass für die Funktion  der Schar
der Schar  gilt:
gilt: 
(4 BE)
2.7
Für alle Werte  mit
mit  gilt
gilt  Deute diese Aussage geometrisch mit Bezug auf den Graphen in der Abbildung 2 und erläutere, was dies im Sachzusammenhang bedeutet.
Deute diese Aussage geometrisch mit Bezug auf den Graphen in der Abbildung 2 und erläutere, was dies im Sachzusammenhang bedeutet.
(3 BE)
3
Betrachtet wird die Funktion  mit
mit
 .
Dabei entsprechen
.
Dabei entsprechen  und
und  den Funktionen aus dem in Aufgabe 1 und 2 beschriebenen Sachzusammenhang. Der Graph von
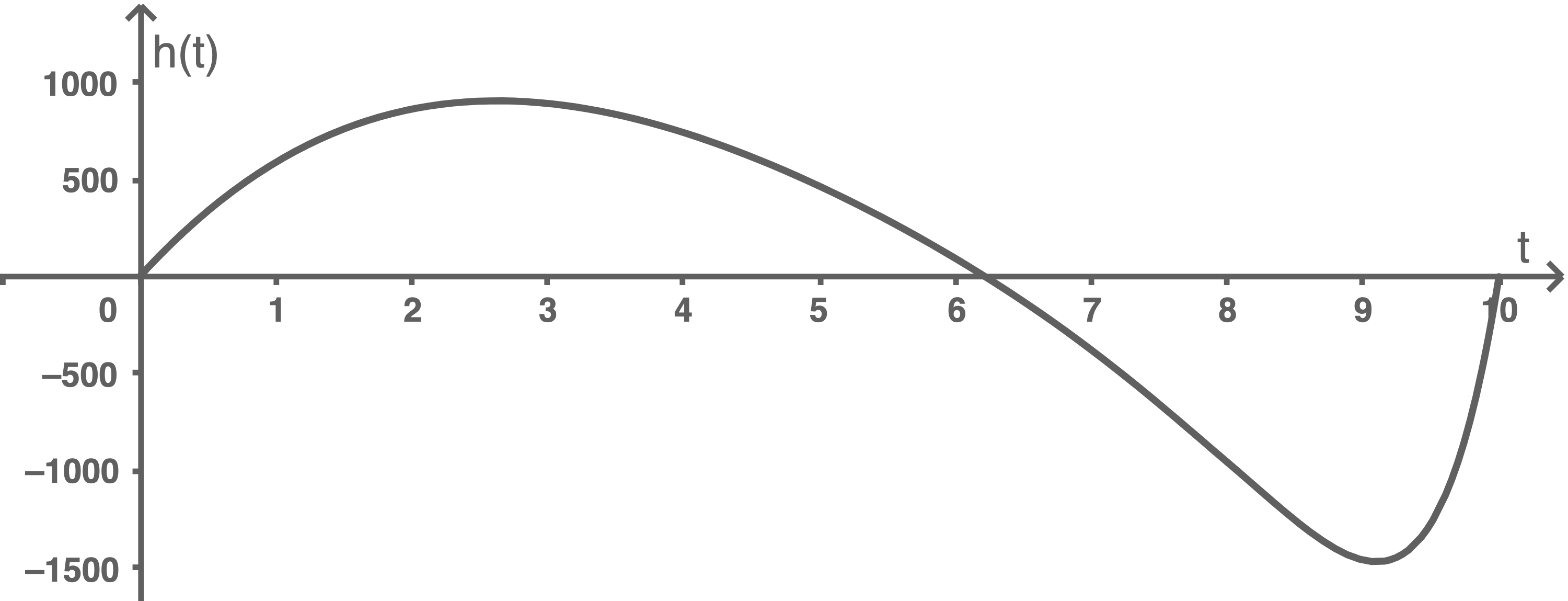
den Funktionen aus dem in Aufgabe 1 und 2 beschriebenen Sachzusammenhang. Der Graph von  ist in Abbildung 3 dargestellt.
ist in Abbildung 3 dargestellt.

Abbildung 3
3.1
Ermittle den Zeitpunkt  an dem sich die meisten Besucher gleichzeitig auf dem Parkgelände befinden.
Beschreibe, wie sich die maximale Besucherzahl auf dem Gelände geometrisch in der Abbildung 3 darstellen lässt.
an dem sich die meisten Besucher gleichzeitig auf dem Parkgelände befinden.
Beschreibe, wie sich die maximale Besucherzahl auf dem Gelände geometrisch in der Abbildung 3 darstellen lässt.
(4 BE)
3.2
Erläutere die Bedeutung der in  definierten Funktion
definierten Funktion  im Sachzusammenhang.
Deute die Ergebnisse in
im Sachzusammenhang.
Deute die Ergebnisse in  und
und  im Sachzusammenhang.
im Sachzusammenhang.


 Stunden
Stunden  5,05 Stunden
5,05 Stunden  5 Stunden 3 Minuten
5 Stunden 3 Minuten
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
An diesem Tag betreten gemäß der Modellierung somit 4096 Besucher den Park.
1.2
Uhrzeit bestimmen
Ableitungsfunktion  angeben:
angeben:
 Notwendige Bedingung für Extremstellen anwenden:
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/b84a48fa2e729a93e6392188a55adf1e628147d1a176cf4f6f763ddc53824bdd?color=5a5a5a) Anwenden der
Anwenden der  -Formel:
Auf die Anwendung der hinreichenden Bedingung für Extremstellen kann verzichtet werden, da die Existenz aus der Aufgabenstellung und aus dem Verlauf des Graphen hervorgeht.
Mit Hilfe von Abbildung 1 lässt sich folgern, dass die Eingangsrate zum Zeitpunkt
-Formel:
Auf die Anwendung der hinreichenden Bedingung für Extremstellen kann verzichtet werden, da die Existenz aus der Aufgabenstellung und aus dem Verlauf des Graphen hervorgeht.
Mit Hilfe von Abbildung 1 lässt sich folgern, dass die Eingangsrate zum Zeitpunkt  maximal ist.
Dies entspricht 2 Stunden und 40 Minuten nach dem Einlass und beschreibt somit die Eingangsrate um 11:40 Uhr.
Aussage prüfen
Durchschnittliche Eingangsrate bestimmen:
maximal ist.
Dies entspricht 2 Stunden und 40 Minuten nach dem Einlass und beschreibt somit die Eingangsrate um 11:40 Uhr.
Aussage prüfen
Durchschnittliche Eingangsrate bestimmen:
![\(\begin{array}[t]{rll}
\dfrac{1}{8}\cdot \displaystyle\int_{0}^{8}f(t)\;\mathrm dt&=& \dfrac{1}{8}\cdot 4096&\\[5pt]
&=& 512
\end{array}\)](https://mathjax.schullv.de/411ae3773ac5324350c82001bfd5090ac234071e01d2988d9b43d5bea4e1380b?color=5a5a5a) Maximale Eingangsrate bestimmen:
Es gilt:
Maximale Eingangsrate bestimmen:
Es gilt:  Die maximale Eingangsrate ist somit um ca
Die maximale Eingangsrate ist somit um ca  größer als die durchschnittliche Eingangsrate.
Die Aussage ist folglich wahr.
größer als die durchschnittliche Eingangsrate.
Die Aussage ist folglich wahr.
1.3
Eine Eingangsrate von 10 Personen pro Minute entspricht der Eingangsrate von 600 Personen pro Stunde.
Es gilt:
![\(\begin{array}[t]{rll}
f(1)&=& 12\cdot 1^3-192\cdot 1^2+768\cdot 1 & \\[5pt]
&=& 588 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/752ccd1a658c85b24dff284f54318871b1b14e01d6b699513aa9579b38fa3d2a?color=5a5a5a)
![\(\begin{array}[t]{rll}
f(5)&=& 12\cdot 5^3-192\cdot 5^2+768\cdot 5 & \\[5pt]
&=& 540 & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1d61761c498be188d8e1e08ce0389e8104e2276326cb172d7db298a953f2d3d9?color=5a5a5a) Aus der Abbildung 1 lässt sich entnehmen, dass für alle
Aus der Abbildung 1 lässt sich entnehmen, dass für alle  bzw.
bzw.  aufgrund des Verlauf des Graphen
aufgrund des Verlauf des Graphen  bzw.
bzw.  gilt.
Somit überschreitet die Eingangsrate nur im angegebenen Zeitraum von 10:00 bis 14:00 den Wert von 600.
Es ist also ausreichend, den zusätzlichen Mitarbeiter in diesem Zeitraum einzubestellen.
gilt.
Somit überschreitet die Eingangsrate nur im angegebenen Zeitraum von 10:00 bis 14:00 den Wert von 600.
Es ist also ausreichend, den zusätzlichen Mitarbeiter in diesem Zeitraum einzubestellen.
2.1
Der Parameter  streckt den Graphen von
streckt den Graphen von  in
in  -Richtung. Für größere bzw. kleinere Werte von
-Richtung. Für größere bzw. kleinere Werte von  werden somit die
werden somit die  -Werte entsprechend größer bzw. kleiner.
Die Graphen von
-Werte entsprechend größer bzw. kleiner.
Die Graphen von  werden durch
werden durch  nicht in
nicht in  -Richtung verschoben bzw. gestreckt. Somit bleiben die
-Richtung verschoben bzw. gestreckt. Somit bleiben die  -Koordinaten der Schnittpunkte mit der
-Koordinaten der Schnittpunkte mit der  -Achse sowie der Extrem- und Wendestellen unabhängig von
-Achse sowie der Extrem- und Wendestellen unabhängig von  konstant.
Der Parameter
konstant.
Der Parameter  hat somit keinen Einfluss auf die Schnittstellen mit der
hat somit keinen Einfluss auf die Schnittstellen mit der  -Achse und verschiebt die Extrem- und Wendepunkte lediglich entlang der
-Achse und verschiebt die Extrem- und Wendepunkte lediglich entlang der  -Achse.
-Achse.
2.2
2.3
Mit der Produktregel folgt:
Für die zweite Ableitung folgt nun:
2.4
Wendestelle berechnen
Notwendige Bedingung für Wendestellen prüfen:
![\(\begin{array}[t]{rll}
g_k](https://mathjax.schullv.de/55e6055edaa61d2c61a63e26506a8db20095e0e4a5b8abf04ee6920957f12db2?color=5a5a5a) Satz vom Nullprodukt anwenden:
Es ist stets
Satz vom Nullprodukt anwenden:
Es ist stets  und
und  also muss
also muss  gelten.s
gelten.s
![\(\begin{array}[t]{rll}
-t^2+6t+18&=& 0&\quad \scriptsize \mid\; \cdot (-1)\\[5pt]
t^2-6t-18&=& 0
\end{array}\)](https://mathjax.schullv.de/aafa1243e3dbc9a9071c7e3d87936987514bd305a1fbc4603b309cf20b5b5494?color=5a5a5a) Anwenden der
Anwenden der  -Formel liefert:
Wegen
-Formel liefert:
Wegen  wird
wird  ausgeschlossen. Die gesuchte Wendestelle entspricht somit
ausgeschlossen. Die gesuchte Wendestelle entspricht somit  Bedeutung der Wendestelle im Sachzusammenhang
Die Wendestelle entspricht der Stelle, an der der Graph der Funktion seine größte Steigung bzw. sein größtes Gefälle annimmt.
Die Wendestelle entspricht somit dem Zeitpunkt, an dem die Ausgangsrate am stärksten zunimmt.
Bedeutung der Wendestelle im Sachzusammenhang
Die Wendestelle entspricht der Stelle, an der der Graph der Funktion seine größte Steigung bzw. sein größtes Gefälle annimmt.
Die Wendestelle entspricht somit dem Zeitpunkt, an dem die Ausgangsrate am stärksten zunimmt.
2.5
1. Schritt: Allgemeine Stammfunktion aufstellen
Da der Term von  zusammengesetzt ist aus einem quadratischen Term und einer
zusammengesetzt ist aus einem quadratischen Term und einer  -Funktion, gilt für mögliche Stammfunktionen
-Funktion, gilt für mögliche Stammfunktionen 
 2. Schritt:
2. Schritt:  ableiten
Weitere Vereinfachung:
ableiten
Weitere Vereinfachung:
 3. Schritt: Koeffizientenvergleich
Es muss
3. Schritt: Koeffizientenvergleich
Es muss  erfüllt sein. Daraus folgt:
erfüllt sein. Daraus folgt:
 Durch einen Koeffizientenvergleich folgt:
Durch einen Koeffizientenvergleich folgt:
 Weiterhin folgt:
Weiterhin folgt:
![\(\begin{array}[t]{rll}
2a+b &=& 10 &\quad \scriptsize \mid\; a=-1\\[5pt]
-2 +b &=& 10 &\quad \scriptsize \mid\; +2\\[5pt]
b &=& 12
\end{array}\)](https://mathjax.schullv.de/d195b162bac433b2fc6df8448dc805f6a049859588add17a911e2e523ec6fe1f?color=5a5a5a) Zudem folgt:
Zudem folgt:
![\(\begin{array}[t]{rll}
b+c &=& 0 &\quad \scriptsize \mid\;b=12 \\[5pt]
12 +c &=& 0 &\quad \scriptsize \mid\; -12 \\[5pt]
c &=& -12
\end{array}\)](https://mathjax.schullv.de/c32a86797ff64978b91ee1072526e209a3f952cf881a9eec619d14edaa770f3b?color=5a5a5a) 4. Schritt: Stammfunktionenschar
4. Schritt: Stammfunktionenschar  aufstellen
Koeffizienten in die allgemeine Stammfunktion
aufstellen
Koeffizienten in die allgemeine Stammfunktion  einsetzen:
einsetzen:

2.6
Begründung
In Aufgabenteil 1.1 wurde bereits berechnet, dass am beobachteten Tag die Anzahl der Besucher 4096 beträgt.
Somit müssen innerhalb der 10 Stunden, in denen der Park geöffnet hat, alle 4096 Personen den Park auch wieder verlassen.
Parameter  bestimmen
bestimmen
2.7
Geometrische Deutung
Der Graph von  nähert sich für
nähert sich für  asymptotisch der
asymptotisch der  -Achse an. Für
-Achse an. Für  verläuft der Graph von
verläuft der Graph von  bereits so nah an der
bereits so nah an der  -Achse, sodass der Inhalt der Fläche, die der Graph von
-Achse, sodass der Inhalt der Fläche, die der Graph von  mit der
mit der  -Achse im Intervall
-Achse im Intervall ![\([0;1]\)](https://mathjax.schullv.de/67b85eab103aec1314a6a9fe5de4b047f5cd37fb49f90a88e9c8c39a6daa39b6?color=5a5a5a) begrenzt, nahezu
begrenzt, nahezu  ist.
Deutung im Sachzusammenhang
In der ersten Stunde nach Einlass verlassen nahezu keine Besucher den Park.
ist.
Deutung im Sachzusammenhang
In der ersten Stunde nach Einlass verlassen nahezu keine Besucher den Park.
3.1
Der Graph der Stammfunktion  von
von  stellt die Besucherzahl dar.
Der Zeitpunkt, an dem sich die meisten Besucher auf dem Gelände befinden, entspricht also der Stelle, an welcher der Graph von
stellt die Besucherzahl dar.
Der Zeitpunkt, an dem sich die meisten Besucher auf dem Gelände befinden, entspricht also der Stelle, an welcher der Graph von  sein Extremum und somit der Graph von
sein Extremum und somit der Graph von  seine Nullstelle annimmt.
Die Nullstelle kann aus der Abbildung 3 abgelesen werden und ist somit etwa durch
seine Nullstelle annimmt.
Die Nullstelle kann aus der Abbildung 3 abgelesen werden und ist somit etwa durch  gegeben.
Etwa 6 Stunden und 9 Minuten nach Öffnung des Parks befinden sich folglich am meisten Besucher auf dem Gelände.
Die maximale Besucheranzahl lässt sich folglich durch den Flächeninhalt zwischen dem Graphen von
gegeben.
Etwa 6 Stunden und 9 Minuten nach Öffnung des Parks befinden sich folglich am meisten Besucher auf dem Gelände.
Die maximale Besucheranzahl lässt sich folglich durch den Flächeninhalt zwischen dem Graphen von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\([0;6,15]\)](https://mathjax.schullv.de/d521ebf2198bace603c131695dd4654c0d02a11d2c554eafd0580b92d65c470e?color=5a5a5a) geometrisch in der Abbildung 3 darstellen.
geometrisch in der Abbildung 3 darstellen.
3.2
Die in  definierte Funktion
definierte Funktion  gibt die Anzahl der Personen an, die zum Zeitpunkt
gibt die Anzahl der Personen an, die zum Zeitpunkt  im Park sind.
Ergebnis
im Park sind.
Ergebnis  beschreibt die durchschnittliche Anzahl der Personen im Park während des beobachteten Tages.
Im Schritt
beschreibt die durchschnittliche Anzahl der Personen im Park während des beobachteten Tages.
Im Schritt  wird die durchschnittliche Aufenthaltsdauer eines Besuchers im Freizeitpark von etwa 5 Stunden und 3 Minuten berechnet.
wird die durchschnittliche Aufenthaltsdauer eines Besuchers im Freizeitpark von etwa 5 Stunden und 3 Minuten berechnet.