Aufgabe 2B
Für ein Land wird die Gruppe derjenigen Personen betrachtet, die im Jahr 2022 eine Urlaubsreise unternahmen.
Aus der betrachteten Gruppe wird eine Person zufällig ausgewählt. Untersucht werden die folgenden Ereignisse:
Die Person ist weiblich.
Die Person war mit ihrer Urlaubsreise zufrieden.
Das nebenstehende Baumdiagramm veranschaulicht die Situation.
Die Person ist weiblich.
Die Person war mit ihrer Urlaubsreise zufrieden.
Das nebenstehende Baumdiagramm veranschaulicht die Situation.
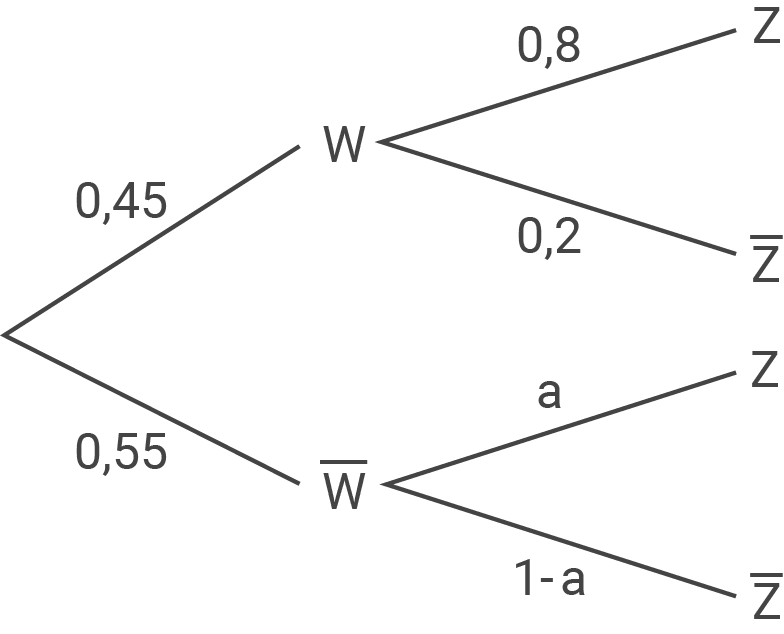
a)
Die Wahrscheinlichkeit dafür, dass eine ausgewählte Person mit ihrer Urlaubsreise zufrieden war, beträgt 
Bestimme den zugehörigen Wert von 
Bestimme den zugehörigen Wert von
(3 BE)
b)
Weise nach, dass es in der betrachteten Gruppe für 
weniger weibliche als nicht weibliche Personen geben würde, die mit ihrer Urlaubsreise zufrieden waren.
weniger weibliche als nicht weibliche Personen geben würde, die mit ihrer Urlaubsreise zufrieden waren.
(2 BE)
c)
Gib denjenigen Wert von 
an, für den 
und 
stochastisch unabhängig sind.
Begründe deine Angabe, ohne zu rechnen.
an, für den und stochastisch unabhängig sind.
Begründe deine Angabe, ohne zu rechnen.
(4 BE)
d)
Die ausgewählte Person war mit ihrer Urlaubsreise nicht zufrieden.
Begründe im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass die Person weiblich ist, mit zunehmendem Wert von zunimmt.
Ein Reiseunternehmen führt ein Gewinnspiel durch. Jede Person kann nur einmal an dem Spiel teilnehmen. Als Ergebnis des Spiels wird eine bestimmte Anzahl von Strandkörben angezeigt. Diese Anzahl beträgt 0, 1, 2 oder 3.
zunimmt.
(3 BE)
Im Folgenden sind die möglichen Gewinne beschrieben:
Bei dem Spiel beträgt der Erwartungswert des Gewinns pro Person 80 Cent.
- Wird kein Strandkorb angezeigt, so gewinnt die Person nichts.
- Werden 1, 2 oder 3 Strandkörbe angezeigt, so gewinnt die Person einen Gutschein.
e)
Berechne die Wahrscheinlichkeit dafür, dass bei dem Spiel kein Strandkorb angezeigt wird.
Bestimme für die Personen mit zwei Strandkörben den Wert des Gutscheins.
(4 BE)
f)
80000 Personen nehmen an dem Spiel teil. Die Zufallsgröße 
beschreibt die Anzahl der Personen mit zwei Strandkörben. Der Erwartungswert der Zufallsgröße wird mit 
bezeichnet.
Ermittle den kleinsten möglichen ganzzahligen Wert von 
für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens 
im Intervall ![\(\left[\mu_Y-c ; \mu_Y+c\right]\)](https://www.schullv.de/resources/formulas/6047778b1fa57b91bdd0841d6d540456c707ba20153056d6dd08eafc37cd5e1c_light.svg)
liegt.
beschreibt die Anzahl der Personen mit zwei Strandkörben. Der Erwartungswert der Zufallsgröße wird mit bezeichnet.
Ermittle den kleinsten möglichen ganzzahligen Wert von für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens im Intervall liegt.
(4 BE)
g)
In der ersten Woche haben 1200 Personen an dem Spiel teilgenommen. Von diesen haben 7 Personen einen Gutschein gewonnen.
Beurteile auf Grundlage einer Sicherheitswahrscheinlichkeit von 
ob die Wahrscheinlichkeit für den Gewinn eines Gutscheins mit dem Ergebnis verträglich ist.
ob die Wahrscheinlichkeit für den Gewinn eines Gutscheins mit dem Ergebnis verträglich ist.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Es soll gelten:
![\(\begin{array}[t]{rll}
P(Z)&=& 0,778 &\\[5pt]
P(W \cap Z) +P(\overline{W} \cap Z) &=& 0,778 & \\[5pt]
0,45\cdot 0,8+0,55\cdot a&=& 0,778 &\quad \scriptsize \mid\; -0,36\\[5pt]
0,55\cdot a&=& 0,418 &\quad \scriptsize \mid\; :0,55\\[5pt]
a&=& 0,76
\end{array}\)](https://www.schullv.de/resources/formulas/496674a7cd79dd408ab202637e9acb7fe03638eab62811f9dc1c9238a36e91dd_light.svg)
b)
Für gilt:
![\(\begin{array}[t]{rll}
P(\overline{W} \cap Z)&=& 0,55\cdot 0,7&\\[5pt]
&=& 0,385
\end{array}\)](https://www.schullv.de/resources/formulas/57eb77c871d362e292f1311fd65e81a4d49868bbdaef0314bd93447ebbce0962_light.svg)
Außerdem gilt:
![\(\begin{array}[t]{rll}
P(W \cap Z)&=& 0,45\cdot 0,8&\\[5pt]
&=& 0,36
\end{array}\)](https://www.schullv.de/resources/formulas/6dc43e2a938c0636509ce3e86d72c18376aa6c221f5f6023798aa3ece807ad23_light.svg)
Wegen 
folgt, dass es weniger weibliche als nicht weibliche Personen geben würde, die mit ihrer Urlaubsreise zufrieden waren.
gilt:
Außerdem gilt:
Wegen folgt, dass es weniger weibliche als nicht weibliche Personen geben würde, die mit ihrer Urlaubsreise zufrieden waren.
c)
und sind stochastisch unabhängig voneinander, wenn unabhängig vom Geschlecht der betrachteten Person die Wahrscheinlichkeit, dass sie mit ihrer Urlaubsreise zufrieden war, gleich ist.
Somit müsste für nicht weibliche Personen ebenso wie für weibliche Personen die Wahrscheinlichkeit, dass die ausgewählte Person mit der Urlaubsreise zufrieden war, 
betragen.
Der gesuchte Wert von beträgt somit 
d)
Mit zunehmendem Wert von steigt die Anzahl der nicht weiblichen Personen, die mit ihrer Urlaubsreise zufrieden waren.
Umso weniger nicht weibliche Personen folglich unzufrieden mit der Urlaubsreise waren, desto größer wird der Anteil der weiblichen Personen an der Gruppe der unzufriedenen Personen.
Somit nimmt die Wahrscheinlichkeit, dass die Person weiblich ist, zu.
steigt die Anzahl der nicht weiblichen Personen, die mit ihrer Urlaubsreise zufrieden waren.
Umso weniger nicht weibliche Personen folglich unzufrieden mit der Urlaubsreise waren, desto größer wird der Anteil der weiblichen Personen an der Gruppe der unzufriedenen Personen.
Somit nimmt die Wahrscheinlichkeit, dass die Person weiblich ist, zu.
e)
Wahrscheinlichkeit berechnen
beschreibt die Anzahl der Strandkörbe, die bei dem Spiel angezeigt werden.
Es gilt:
Wert des Gutscheins bestimmen
Da der Erwartungswert des Spiels 80 Cent betragen soll, folgt:
Der Wert des Gutscheins bei zwei Strandkörben beträgt somit 
beschreibt die Anzahl der Strandkörbe, die bei dem Spiel angezeigt werden.
Es gilt:
Wert des Gutscheins bestimmen
Da der Erwartungswert des Spiels 80 Cent betragen soll, folgt:
Der Wert des Gutscheins bei zwei Strandkörben beträgt somit 
![\(\begin{array}[t]{rll}
P(X=0)&=& 1-P(X=1)-P(X=2)-P(X=3)& \\[5pt]
&=& 1-0,01-0,001-0,0001 & \\[5pt]
&=& 0,9889
\end{array}\)](https://www.schullv.de/resources/formulas/04bd02d354ce34af0ea53debcedd9383b8d9784334614761ec9d742aba472499_light.svg)
![\(\begin{array}[t]{rll}
0,01\cdot 50+0,001\cdot x+0,0001\cdot 1000&=& 0,8 & \\[5pt]
0,001\cdot x+ 0,6&=& 0,8 &\quad \scriptsize \mid\; -0,6 \quad \scriptsize \mid\;:0,001 \\[5pt]
x&=& 200
\end{array}\)](https://www.schullv.de/resources/formulas/d9c04f083c7653e8ea72848c8ff57d4fec19f0bc1f56fd356b783f6256bfbafa_light.svg)
f)
beschreibt die Anzahl der Personen mit zwei Strandkörben und ist binomialverteilt mit 
und 
Es soll nun gelten:
![\(\begin{array}[t]{rll}
P(\mu_Y-c \leq Y \leq\mu_Y +c)&\geq& 0,8 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/31459be73c59eadc9baa2d049fa9499c57bb4bf643ca9dfeaba147e6c57d76e1_light.svg)
Systematisches Ausprobieren mit dem CAS liefert:
Der kleinstmögliche Wert von 
![\(\begin{array}[t]{rll}
P( 80-10 \leq Y \leq 80+10)&=& P(Y\leq 90)-P(Y\leq 69) & \\[5pt]
&\approx& 0,879-0,118& \\[5pt]
&=& 0,761
\end{array}\)](https://www.schullv.de/resources/formulas/5815a34d84a1be81c7022bd2b6b9089d2d3fdaba03cd9e49f855726c7354b564_light.svg)
![\(\begin{array}[t]{rll}
P( 80-11 \leq Y \leq 80+11)&=& P(Y\leq 91)-P(Y\leq 68) & \\[5pt]
&\approx& 0,899-0,097& \\[5pt]
&=& 0,802
\end{array}\)](https://www.schullv.de/resources/formulas/c27e8082d8570ca1ce3ed84c1e6d11dc17fa5237d5a9f8ea871a2f7631de37ab_light.svg)
für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens 
im Intervall ![\([\mu_Y-c ; \mu_Y+c]\)](https://www.schullv.de/resources/formulas/c5042bd5a7a0e735e421977d5d2cbcae8276649546ffe98c7b4b3d3a9aa0dfb9_light.svg)
liegt, ist somit gegeben durch 
g)
Für das Konfidenzintervall soll gelten:
Es folgt also:
Somit ergibt sich:
Das CAS liefert nun 
Entsprechend der gegebenen Informationen beträgt die Gewinnwahrscheinlichkeit für einen Gutschein 
und ist damit mit dem Ergebnis verträglich.
Ausgehend von den gegebenen Wahrscheinlichkeiten ist auch eine Beurteilung mittels eines Prognoseintervalls möglich.
Hinweis: Bei Verwendung anderer Näherungsverfahren können sich abweichende Ergebnisse ergeben.
![\(\begin{array}[t]{rll}
P(\mu - 2,58\cdot \sigma \leq X \leq \mu + 2,58\cdot\sigma)& \approx & 0,99& \\[5pt]
P\left(n\cdot p - 2,58\cdot \sqrt{n\cdot p \cdot(1-p)} \leq X \leq n\cdot p +2,58\cdot\sqrt{n\cdot p \cdot(1-p)} \right)& \approx & 0,99& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/59f969606baab112834d55d0d37339de4ee6e8f3590426e7e3c7b9d04d58981c_light.svg)
![\(\begin{array}[t]{rll}
n\cdot p - 2,58\cdot \sqrt{n\cdot p \cdot(1-p)}&\leq& \quad \quad X & \leq & n\cdot p +2,58\cdot\sqrt{n\cdot p \cdot(1-p)} &\quad \scriptsize \mid\; :n \\[5pt]
p - 2,58\cdot \sqrt{\dfrac{p \cdot(1-p)}{n} }&\leq& \quad \;\; \dfrac{X}{n} &\leq& p +2,58 \cdot\sqrt{\dfrac{ p \cdot(1-p)}{n}} &\quad \scriptsize \mid\; -p \\[5pt]
- 2,58\cdot \sqrt{\dfrac{p \cdot(1-p)}{n} }&\leq& \; \; \dfrac{X}{n}-p &\leq& 2,58 \cdot\sqrt{\dfrac{ p \cdot(1-p)}{n}} &\quad \scriptsize \mid\;X=7 \quad \scriptsize \mid\;n=1200 \\[5pt]
- 2,58\cdot \sqrt{\dfrac{p \cdot(1-p)}{1200} } &\leq& \dfrac{7}{1200}-p &\leq& 2,58 \cdot\sqrt{\dfrac{ p \cdot(1-p)}{1200}} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/20662f81f0b3d5646e53399368068c2db217013c6373894109bce0d4fabe0059_light.svg)
![\(\begin{array}[t]{rll}
\,\bigg \vert \, \dfrac{7}{1200}-p \,\bigg \vert \, &\leq & 2,58 \cdot\sqrt{\dfrac{ p \cdot(1-p)}{1200}} &\quad \scriptsize \,\bigg \vert \,\; (\,)^2 \\[5pt]
\left(\dfrac{7}{1200}-p\right)^2&=& 2,58^2 \cdot \dfrac{ p \cdot(1-p)}{1200}
\end{array}\)](https://www.schullv.de/resources/formulas/217b4774b677d33b16bd9e3c48e1494243871ce7d51595280ab18ffcee792e59_light.svg)
Entsprechend der gegebenen Informationen beträgt die Gewinnwahrscheinlichkeit für einen Gutschein und ist damit mit dem Ergebnis verträglich.
Ausgehend von den gegebenen Wahrscheinlichkeiten ist auch eine Beurteilung mittels eines Prognoseintervalls möglich.
Hinweis: Bei Verwendung anderer Näherungsverfahren können sich abweichende Ergebnisse ergeben.